5.3. Равномерное распределение
Непрерывная
случайная величина Х
имеет равномерное
распределение,
если в интервале ее возможных значений
плотность распределения вероятности
сохраняет постоянное значение, то есть
Параметр
С
можно найти, используя свойство
дифференциальной функции (плотности
распределения):
;
;
;
отсюда
.
Таким образом,
Построим график дифференциальной функции (рис. 11).
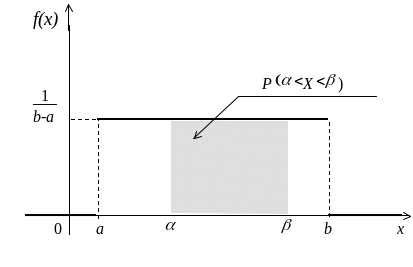
Рис. 11
Найдем интегральную функцию распределения по формуле
При
При
При
Итак,
Построим график интегральной функции (рис. 12).
Найдем числовые характеристики данного распределения.
Рис. 12
.
Найдем
вероятность
попадания значений случайной величины
в интервал
,
где
.
.
Таким
образом, вероятность
численно равна отношению длины отрезка
ко всей длине отрезка
,
на котором задано равномерное
распределение. Из полученной формулы
следует: где бы ни располагался отрезок
,
вероятность
не меняется, если не меняется длина
отрезка
.
Графически эта вероятность показана
на графике дифференциальной функции
(заштрихованная площадь на рис. 11) .
Примечание. Равномерное распределение можно рассматривать как распространение идеи "равновозможности исходов" на случай непрерывной случайной величины, когда известно, что в пределах некоторого интервала все значения случайной величины одинаково вероятны, то есть обладают одной и той же плотностью вероятности.
Примером случайной величины, имеющей равномерное распределение, будет погрешность округления при выполнении вычислений, а также время, прошедшее от начала данного часа до поломки часов, и т.д.
Отметим, что равномерное распределение не обладает свойством устойчивости, то есть сумма двух независимых случайных величин, каждая из которых имеет равномерное распределение, имеет закон распределения, отличный от равномерного.
Пример 33. Автобусы некоторого маршрута идут строго по расписанию с интервалом движения 8 мин. Время, в течение которого пассажиру приходится ждать автобус, представляет собой случайную величину, распределенную равномерно.
Записать дифференциальную и интегральную функции распределения, построить их графики; найти математическое ожидание и среднее квадратическое отклонение; вычислить вероятность того, что пассажир будет ожидать очередной автобус менее 5 мин.
Решение. Случайная величина Х - время, в течение которого пассажир ожидает очередного автобуса. По условию задачи, эта случайная величина распределена равномерно в интервале (0,8).
По определению равномерного распределения запишем дифференциальную функцию:
Тогда:
Построим
графики функции
и
(рис. 13, 14).
(пассажир
ожидает очередной автобус в среднем 4
мин).
.
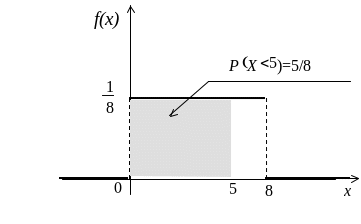
Рис. 13
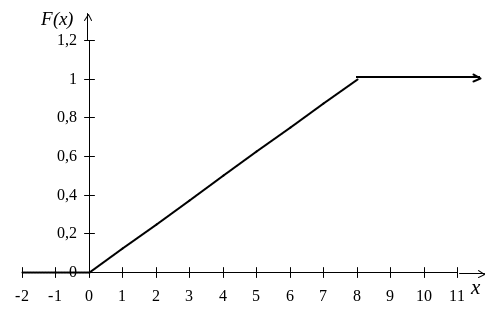
Рис. 14
.
Таким образом, вероятность того, что пассажир ожидает очередной автобус менее 5 мин, равна 0,625.
Искомую
вероятность можно вычислить и с помощью
интегральной функции распределения.
.
5.4. Показательное распределение
Непрерывная случайная величина Х имеет показательный закон распределения, если ее плотность распределения вероятности имеет вид
где
- постоянная положительная величина,
называемая параметром
распределения.
Убедимся,
что такое определение показательного
закона корректно, то есть выполняется
условие
.
Действительно,
(здесь
учтено, что
>0
и
).
График дифференциальной функции распределения представлен на рис. 15.
Рис. 15
Найдем интегральную функцию распределения по формуле
.
При
При
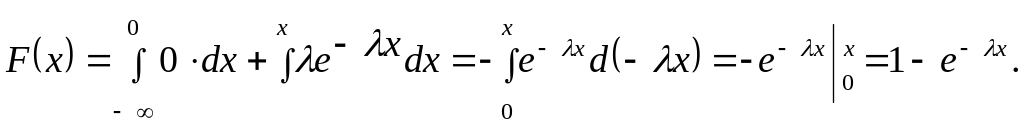
Итак,
График интегральной функции представлен на рис. 16.
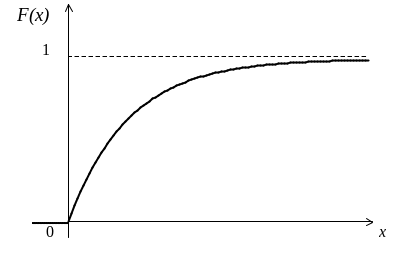
Рис. 16
Найдем
вероятность попадания случайной
величины Х
в интервал
,
где
.
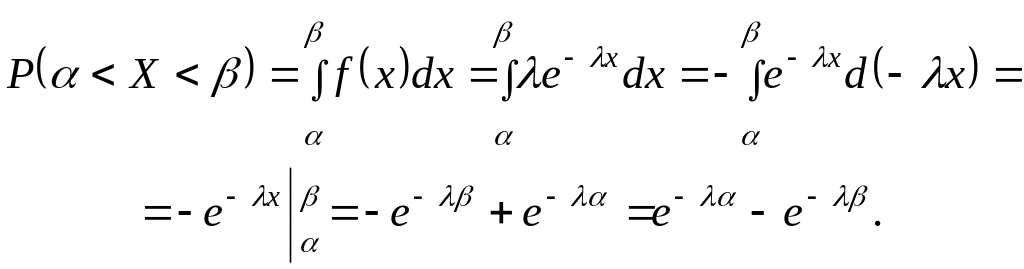
Итак,
(Значения
функции
приведены
в прил. 7.)
Далее найдем числовые характеристики показательного распределения, используя метод интегрирования по частям.
=
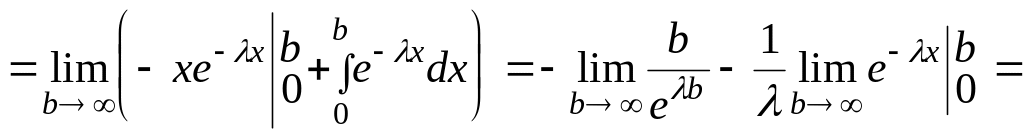
Итак,
.
Дисперсию
вычислим по формуле
.
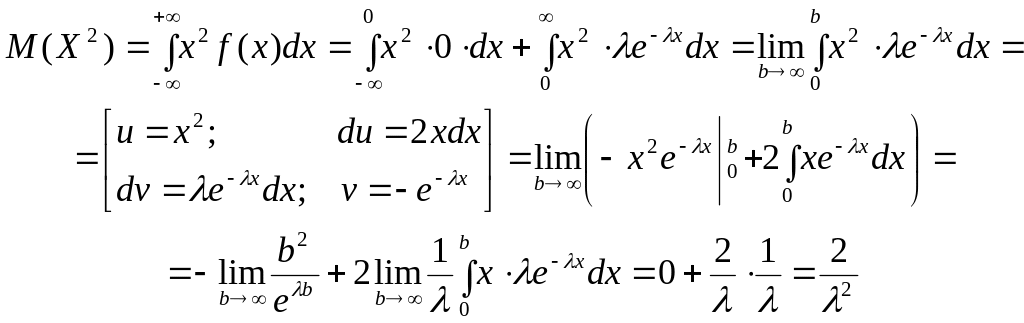
(второй интеграл вычислен выше).
Следовательно,
,
.
Таким
образом,
,
,
.
Равенство
известно как характеристическое
свойство
показательного распределения. Отметим
его практическое применение. Допустим,
мы имеем непрерывную случайную величину
Х,
закон распределения которой неизвестен.
По выборочным данным находятся оценки
математического ожидания
и среднего квадратического отклонения
.
Если эти оценки окажутся близкими, то
можно предположить, что случайная
величина имеет показательное распределение.
Показательное распределение широко используется в теории надежности, изучающей условие безотказной работы некоторой системы, если отказы в ее работе образуют простейший поток.
Пусть
непрерывная величина Т
- длительность времени безотказной
работы некоторого элемента, имеющая
показательное распределение. Тогда
интегральная функция этого распределения
,
где
.
Если элемент проработал безотказно время, менее t, то можно сказать, что за время длительностью t наступил отказ.
Так
как функция распределения
есть вероятность отказа элемента за
время длительностью t,
то время безотказной работы элемента
за это же время длительностью t
будет противоположным событием, то есть
,
а вероятность безотказной работы
.
Функцию
обозначают
и называют функцией
надежности.
Итак,
- функция надежности, определяющая
вероятность безотказной работы элемента
за время t.
Пример 34. На шоссе установлен контрольный пункт для проверки технического состояния автомобилей. Время ожидания машины контролером имеет показательное распределение со средним значением 0,1 ч.
Записать плотность распределения вероятности данного распределения, найти его характеристики, а также вероятность того, что контролер будет ждать очередную машину менее 1 мин.
Решение. Случайная величина Х - время ожидания машины контролером, по условию задачи она имеет показательное распределение.
Найдем
параметр
этого распределения. По условию,
ч. Так как
,
то параметр
.
Плотность распределения вероятности данного распределения
Найдем характеристики рассеяния этой случайной величины:
и
Найдем
вероятность того, что контролер будет
ждать очередную машину менее 1 мин, то
есть менее
ч.
.
Пример
35.
Испытывают
два независимо работающих элемента.
Длительность времени безотказной работы
элементов (в часах) имеет показательное
распределение с параметрами, соответственно,
и
.
Найти вероятность того, что за время длительностью t=6 ч: а) оба элемента откажут; б) хотя бы один элемент не откажет; в) оба элемента не откажут.
Решение.
Случайная величина Х
- время безотказной работы первого
элемента - имеет показательное
распределение с параметром
.
Случайная величина У - время безотказной работы второго элемента - имеет показательное распределение с параметром . Их дифференциальные функции распределения вероятностей следующие:
Событие А1 - откажет первый элемент за все время t=6, то есть Х<6.
Событие А2 - откажет второй элемент за время t=6, то есть Y<6 .
.
Событие А - откажут оба элемента (и первый, и второй).
.
Событие В - хотя бы один элемент не откажет (или один, или два).
Событие
- оба элемента откажут.
Событие С - оба элемента не откажут (и первый, и второй).
.
.
.