Глава 5 виды распределений

5.1. Биномиальное распределение

Пусть проводится n независимых испытаний, причем вероятность наступления некоторого события А в каждом испытании постоянна и равна р, то есть . При этом событие А может наступить ноль раз (ни разу), или 1, или 2, или ..., или m, ... , или n раз в зависимости от случайных обстоятельств. Следовательно, частота наступления события А есть величина случайная, причем дискретная. Обозначим ее через Х и составим закон распределения вероятности случайной величины Х, который представим в виде следующей таблицы:

	0	1	2	...	m	...	n-1	n
				...		...			.

Рассмотрим каждое значение случайной величины как событие. Найдем соответствующие вероятности , используя формулу Бернулли.

Событие А₁ - ноль раз наступит событие А в n независимых испытаниях с вероятностью р при каждом испытании, тогда

.

Событие А₂ - один раз наступит событие А в n независимых испытаниях с вероятностью р при каждом испытании.

.

Проводя аналогичные рассуждения, находим

,

Составленный закон распределения называется биномиальным законом распределения. Такое название объясняется тем, что вероятности являются членами разложения бинома Ньютона: .

Нетрудно убедиться, что данное определение биномиального закона корректно, ибо

.

Интегральная функция распределения вероятности биномиального закона имеет вид

Биномиальное распределение обладает следующими свойствами: с возрастанием частоты m от 0 до n вероятности сначала растут до некоторого момента, а потом начинают убывать. Это распределение асимметрично, кроме случая, когда р=0,5.

На рис. 9 изображены полигоны биномиального распределения вероятностей при различных n и р=0,4.

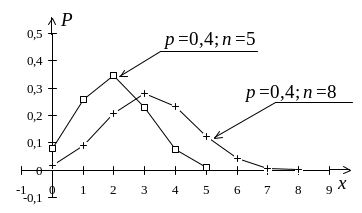
Рис. 9

Из рис. 9 наглядно видно, что при возрастании m вероятности сначала растут и достигают наибольшего значения, а затем начинают убывать.

Определение. Частота наступления события , которой соответствует наибольшая вероятность , называется наивероятнейшей частотой и обозначается m₀, то есть и .

Найдем m₀ из этих двух неравенств, используя формулу Бернулли.

После преобразований система неравенств примет вид

или

Решая систему неравенств относительно m₀ , получим

Отсюда .

Числа и отличаются на 1, они могут быть целыми или дробными. Если они дробные и отличаются на 1, то (где - обозначение целой части числа), а если эти числа - целые, то имеет два значения: и . При достаточно большом n наивероятнейшая частота становится близка к , то есть .

Найдем числовые характеристики случайной величины Х.

В скобках имеем разложение бинома , поэтому

.

Аналогично найдем дисперсию .

.

.

Так как случайная величина Х выражает частоту m наступления события в n независимых испытаниях, то можно записать:

; .

Замечание. Полученные свойства биномиального закона распределения позволяют пояснить смысл аргумента х функции f(x), используемой в асимптотической формуле Муавра - Лапласа. Для этого рассмотрим случайную величину Х, имеющую биномиальное распределение с числовыми характеристиками и . Тогда аргумент представляет собой отклонение числа m появлений события А в n независимых испытаниях от среднего значения рассматриваемой случайной величины, приходящееся на единицу среднего квадратического отклонения.

Частость события А при n независимых испытаниях также будет случайной величиной. Найдем характеристики этой случайной величины.

.

.

Пример 31. Вероятность того, что телевизор не потребует ремонта в течение гарантийного срока, равна 0,8. Составить закон распределения числа телевизоров, потребующих гарантийного ремонта, из трех проданных телевизоров.

Решение. Вводим обозначения. Случайная величина Х - число телевизоров, потребующих гарантийного ремонта, из трех проданных телевизоров. Случайная величина дискретная. Событие А - телевизор потребует гарантийного ремонта.

Составим закон распределения случайной величины Х:

	0	1	2	3	.
	0,512	0,384	0,096	0,008

Пусть событие - ни один из трех телевизоров не потребует ремонта, то есть ноль телевизоров потребуют ремонта, тогда

.

Пусть событие - один телевизор из трех потребует ремонта.

.

Аналогично рассуждая, находим остальные вероятности.

.

.

Составленный закон распределения - биномиальный.

Проверим корректность составленного ряда распределения:

0,512+0,384+0,095+0,008=1.

Построим полигон распределения (рис. 10).

Рис. 10

Пример 32. Вероятность того, что на сборку попадает прибор, удовлетворяющий стандарту, равна 0,8. Найти наивероятнейшее число стандартных приборов из 150 поступивших и вероятность поступления такого числа приборов.

Решение. Событие А - на сборку поступил прибор, удовлетворяющий стандарту. ; n=150,

Наивероятнейшее число стандартных приборов из 150 найдем по формуле .

150·0,8 -0,2 150·0,8 +0,8; 119,8 120,8.

Отсюда =120.

Далее найдем вероятность того, что из 150 поступивших приборов 120 - стандартных. Так как число испытаний n=150 достаточно велико, а npq=24 20, то найдем по формуле Муавра - Лапласа

, где .

Вычислим . Используя таблицу значений функции f(x) (прил. 1), имеем .

Отсюда .