Министерство науки и образования Украины

Сумской государственный университет

ОДЗ по предмету:

«Математические модели и модели энергетического оборудования»

На тему:

«Решение дифференциального уравнения методом Эйлера и методом Рунге-Кутта»

Выполнила Шатилова Т. А.

Группа Х-81

Проверил Мелейчук С. С.

Сумы 2010

Содержание

с

1. Исходные данные….…………………………………………………………………….…………………..….………………………………..3

2. Подготовка данных для расчета ………………………………………………………………………………………..…......…4

3. Описание метода Эйлера………………………………… ………………………………………………………………...…………...5

4. Программа расчета методом Эйлера …………………………………………………………………………….…………….9

5. Вывод результатов расчета методом Эйлера …………………………………..…………………………..……....10

6. Описание метода Рунге-Кутта……………………………………………………………………………………………….……11

7. Программа расчета методом Рунге-Кутта……………………………………………………………………………….12

8. Вывод результатов расчета методом Рунге-Кутта……………………………………………………….…….13

9. Анализ результатов………………………………………………………………………………………………………………………..14

10. Литература…………………………………………………………………………………………………………………………………..……15

1. Исходные данные

Решить методом Эйлера следующие дифференциальное уравнение:

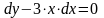
При следующих условиях:

;

.

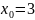
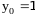L =1; h = 0,1

2. Подготовка исходных данных для расчета

   1. Запишем исходную функцию и дифференцируем ее:

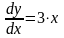
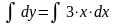
Подставляем начальные условия:

3. Краткое описание метода Эйлера

Метод Эйлера является простейшим методом решения задачи Коши.

По условию задачи Коши, требуется найти функцию У=У(х), удовлетворяющую уравнению

У'=f(x,Y) (3.1)

И принимающую при заданное значение :

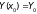(3.2)

При этом будем для определенности считать. Что решение нужно получить для значений .

Согласно теореме Коши решение У (х) задачи (3.1) и (3.2) существует единственно и является гладкой функцией, если правая часть f(х,У) уравнения (3.1), являющаяся функцией двух переменных х, У, удовлетворяет некоторым условиям гладкости. Будем считать, что эти условия выполнены и существует единственное гладкое решение У(х).

Рассмотрим метод Эйлера, как метод решения простейшего дифференциального уравнения. Рассмотрим уравнение (3.1) в окрестностях узлов 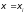(i = 0,1,…) и заменив левой части производную У' правой разностью:

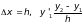, (3.3)

При этом значения функции У в узлах 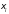заменим значениями сеточной функции :

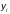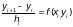(3.4)

Полученная аппроксимация дифференциального уравнения (3.1) имеет первый порядо, поскольку при замене (3.1) на (3.4) допускается погрешность 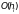- при численном дифференцировании функции, заданной в виде таблицы с шагом h, эта погрешность зависит от h и ее записывают в виде:

(3.5)

(О большее от )

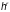Показатель степени r называется порядком погрешности аппроксимации производной или порядком точности данной аппроксимации. При этом предполагается, что значение шага по модулю меньше единицы.

Оценку погрешности легко иллюстрировать с помощью ряда Тейлора:

(3.6)

Будем считать для простоты узлы равностоящими, т.е. . Тогда из равенства (3.4) получаем:

(3.7)

Заметим, что из уравнения (3.1) следует:

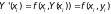(3.8)

Поэтому (3.7) представляет собой приближенное нахождение значение функции У в точке при помощи разложения в ряд Тейлора с отбрасыванием членов второго и более высоких порядков. Другими словами, приращение функции полагается равным ее дифференциалу.

Полагая i=0, с помощью соотношения (3.7) находим значение сеточной функции :

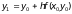
Требуемое здесь значение заданно начальным условием (3.2), т.е.:

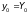(3.9)

Аналогично могут быть найдены значения сеточной функции в других узлах:

……………………………….

Построенный алгоритм и является методом Эйлера. Расностная схема этого метода предоставлена соотношениями (3.9) и (3.8). Они имеют вид рекуррентных формул. С помощью которых значение сеточной функции 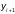в любом узле вычисляется по его значению в предыдущем узле . В связи с этим метод Эйлера относиться к одношаговым методам.

Рис. 3.1 - Структурограмма алгоритма решения задачи Коши

Задаются начальные значения , и величина шага h с количеством расчетных точек n. Решение получается в узлах x+h, x+2h,…x+nh. Вывод результатов предусмотрен на каждом шаге. Если найденные значения необходимо хранить в памяти машины, то следует ввести массив значений

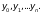
Приведенным алгоритмом можно воспользоваться и в случае, если требуется найти решение задачи Коши на отрезке [a,b] при начальном условии в точке x=a.

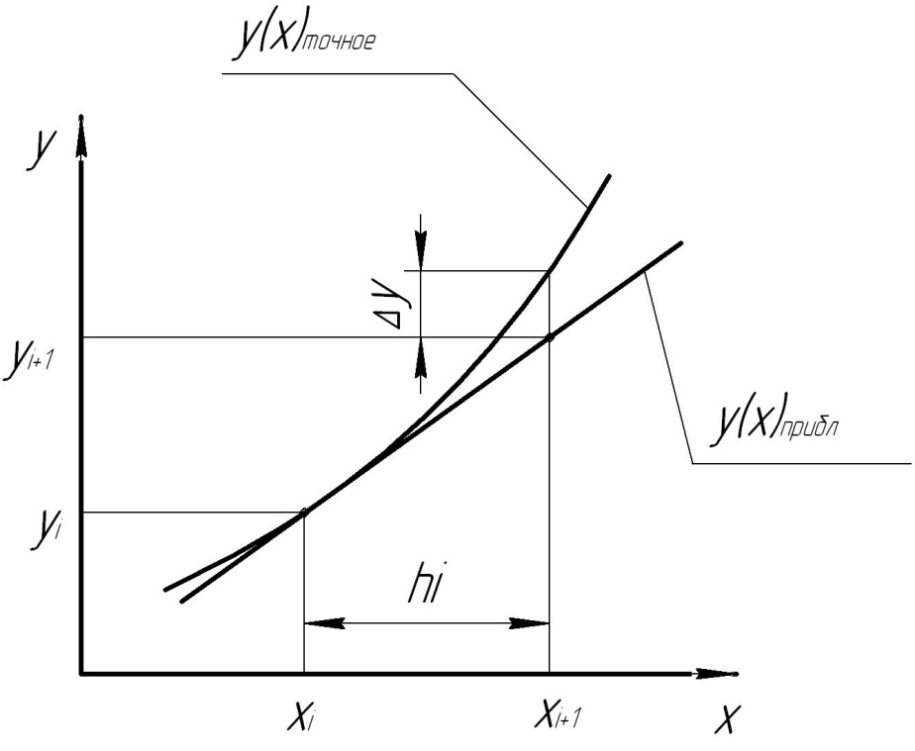
Рис. 3.2 – Геометрическая интерпретация метода Эйлера

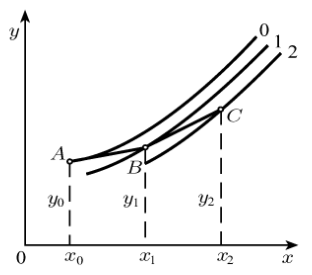
Изображены только первые 2 шага, т.е. иллюстрировано вычисление сеточной функции в точках . Интегральные кривые 0, 1, 2 описывают точные решения уравнения (3.1). При этом кривая 0 соответствует точному решению задачи Коши (3.1), (3.2), т.к. она проходит через начальную точку А . Точки В, С получены в результате численного решения задачи коши методом Эйлера. Их отклонения от кривой 0 характеризуют погрешность метода. При выполнении каждого шага мы фактически попадаем на другую интегральную кривую. Отрезок АВ – отрезок касательной к кривой 0 в точке А, ее аклон характеризуется значением производной . 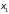Погрешность появляется потому, что приращении значения функции при переходе от к заменяется приращением ординаты касательной кривой 0 в точке А. касательная кривая АВ уже проводиться к другой интегральной кривой 1. Т.о погрешность метода приводит к тому, что на каждом шаге приближенное значение переходит на другую интегральную кривую.