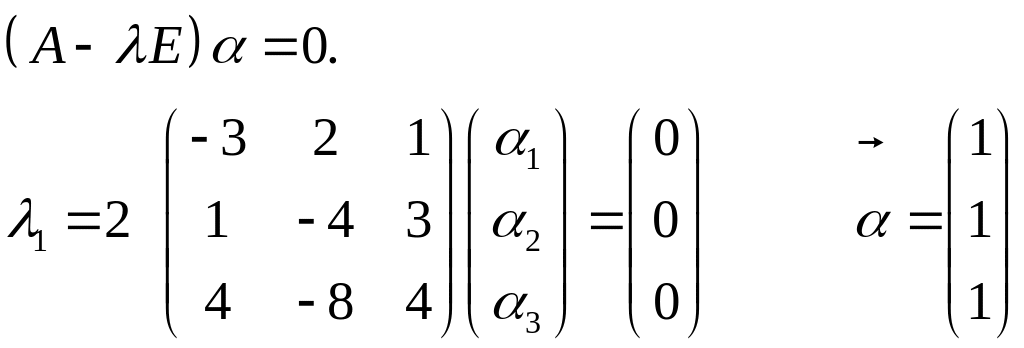§13 Линейные системы

― коэффициенты системы определены и

― свободные члены системы непрерывны на .

Если , то система однородна, иначе ― неоднородна.

дифференцирование матрицы ― поэлементно.

― матрица системы

.

Тогда

Если , то однородная.

― однородная.

― неоднородная.

Начальные условия:

.

Свойство: решение задачи Коши. .

Определение: 1. ― линейно зависимы на , если , не все равные нулю, что .

Если лишь при всех , то линейно независимы.

2. Определитель Вронского(вронскиан) для

3. Фундаментальная система решений ― совокупность линейно независимы вектор-столбцов, являющихся решением .

4. Фундаментальная матрица ― матрица, столбцы которой образуют фундаментальную систему решений . Обозначается .

Теоремы:

1. Пусть линейно зависимы. Тогда .

2. ― решения и линейно независимы.

3. ―решения . Тогда справедливо ровно одно из следующих утверждений:

а.

б.

4. системы фундаментальная система решений.

5. Формула общего решения имеет вид:

, где

― фундаментальная система решений.

Доказательство аналогично предыдущим.

Общее решение: , где .

Общего метода для нахождения фундаментальной системы решений нет.

Неоднородная система

Метод Лагранжа. Сначала надо узнать фундаментальную систему решений соответствующей

( знаем соответствующую ).

Тогда . Надо найти .

Для матриц и .

Пусть ― фундаментальная система решений ( состоит из них).

― равенства столбцов.

Возьмем левые части равенств, сформируем из них матрицу. Получим . Сформируем матрицу из правых столбцов. вынесем за знак матрицы. Справа будет .

.

Тогда

У фундаментальной матрицы всегда существует (т.к. , а для фундаментальной системы решений (по т.3, а фундаментальная система решений ― линейно независима), т.е. существует ).

Домножим слева на .

.

Осталось обосновать, что ― все решения.

Пример:

; ; . .

,

.

. Лучше через .

;

;

.

Ответ: ,

,

.

§14 Линейные однородные системы с постоянными коэффициентами. ( )

,

― фундаментальная система решений системы ( ― вектор !)

― общее решение .

Формулы для фундаментальной системы решений разные в зависимости от :

1. Собственные значения . Можно указать три линейно независимых собственных вектора матрицы . Тогда ― собственные значения , соответствующие ( не обязательно различны)

2. Собственные значения . Можно указать три линейно независимых вектора

― собственные векторы , ― присоединенный вектор к собственному вектору . Тогда . , где ― собственные значения, отвечающие соответствующим и .

3. Собственные значения . Можно указать три линейно независимых вектора .

― собственный вектор , ― соответственно 1,2 присоединенные векторы к . Тогда .

― собственное значение, соответствующее .

4. Пусть у существует одно собственное значение , два комплексно сопряженных собственных значения .

― какой-либо собственный вектор, отвечающий .

― какой-либо собственный вектор, отвечающий .

Тогда .

Для реализуется ровно 1 из 4 случаев.

Доказательство(для 2-го случая):

Докажем, что ― решения . Тогда .

Так как

― истинное равенство, так как выражает определение собственных векторов и собственных значений .

― истинно, так как следует из определения .

Тогда преобразуется в:

По определению присоединенного вектора:

Значит истинно.

Найдем .Докажем, что линейно независимы:

― линейно независимы.

Вронскиан от при . По теореме 2 предыдущего параграфа линейно независимы. Т. е. ― фундаментальная система решений. ЧТД.

Пример 1:

Характеристическое уравнение .

……….

Так как все и различны, то существуют три собственных вектора для разных (они линейно независимы, так как соответствуют разным ).

Как находить собственные векторы:

― собственный вектор