§11 Линейные неоднородные уравнения.

. Определены и непрерывны на . . .

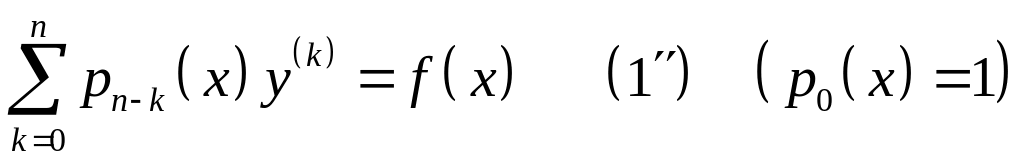Свойства уравнения (1):

1. (общее решение = частное + общее соответствующего однородного)

2. Если , то Это свойство распространяется на любое число слагаемых.

3. решение уравнения (1), , такое, что .

I. Метод Лагранжа (метод вариации производных):

1. ф.с.р .

2. Записать и решить следующую систему алгебраических уравнений:

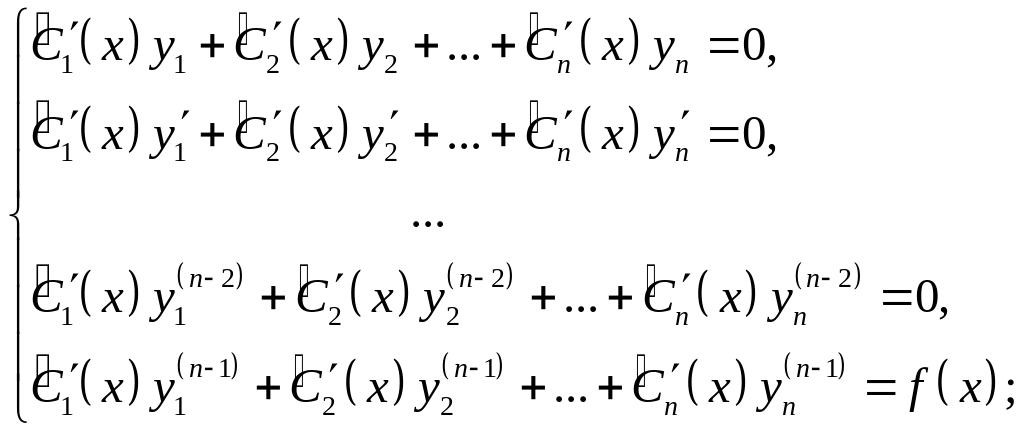
!!В исходном уравнении перед производной высшего порядка должна стоять 1!!, иначе найдется неправильно!

Решаем систему и находим . (т.к. фундаментальная система решений), т.е. решение. (Задача Коши – просто подставляем и находим ). .

3. .

Доказательство:

Надо показать, что 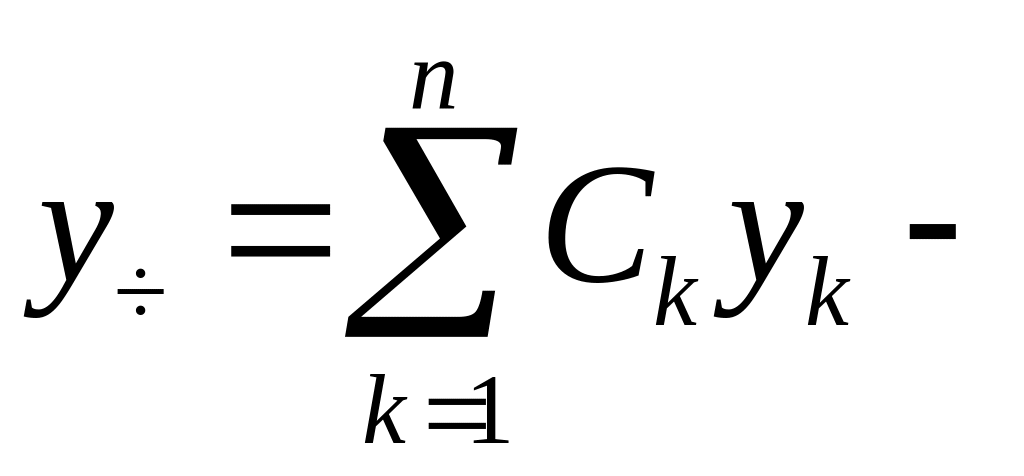частное решение (1).

Т.к. первое уравнение системы, а удовлетворяет системе

Т.к. второе уравнение системы

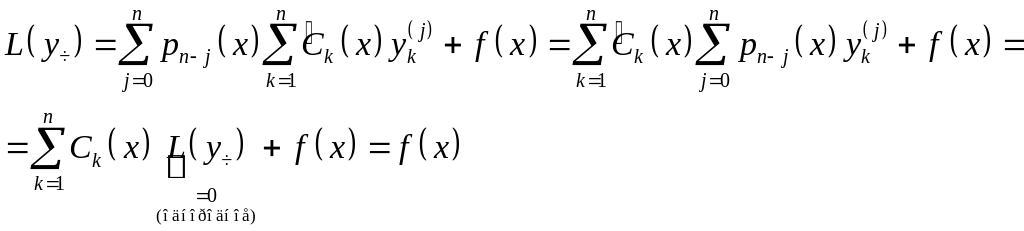
II. Метод неопределенных коэффициентов (без доказательства), находит .

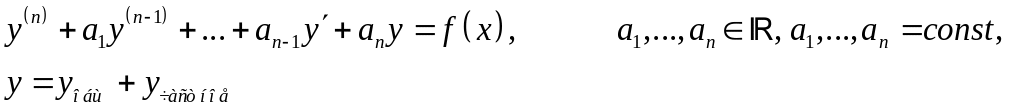
Применяется для любых .

1. ;

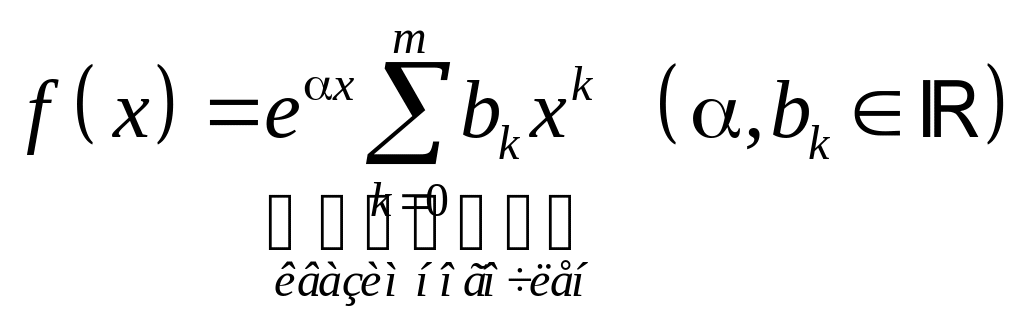, если не является корнем соответствующего характеристического уравнения, иначе равно кратности .

Сначала не определены. После подстановки в исходное уравнение они находятся. Известно, что всегда найдется и притом единственным образом.

Пример:

сразу в ответе.

Тогда

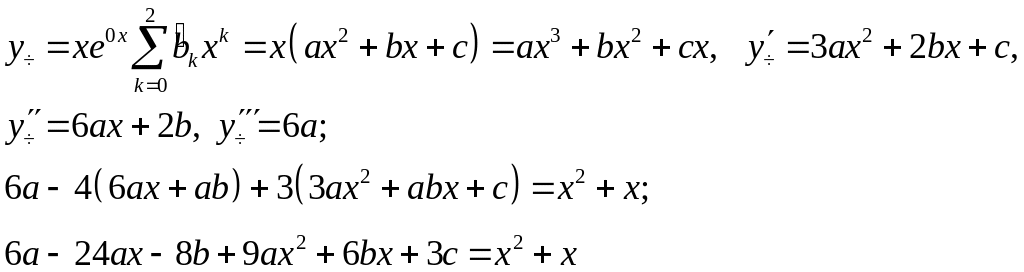
Ответ: .

2)

.

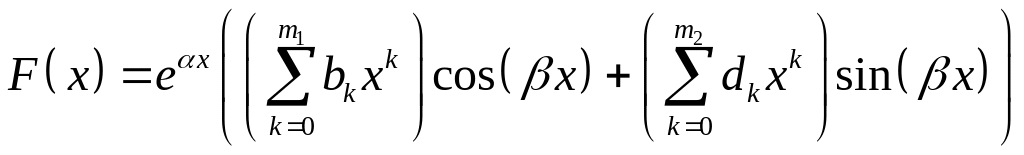
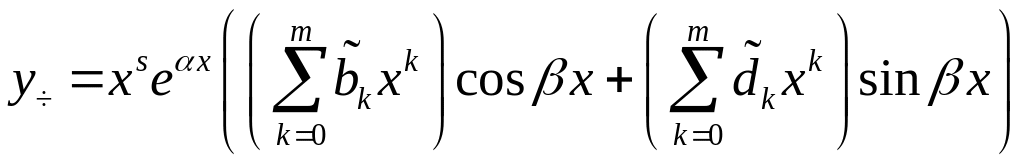, если ― не корни соответствующего характеристического уравнения, равно кратности этих корней.

Сначала ― неизвестные. Находятся подстановкой в исходное уравнение.

Пример:

― не корни .

.

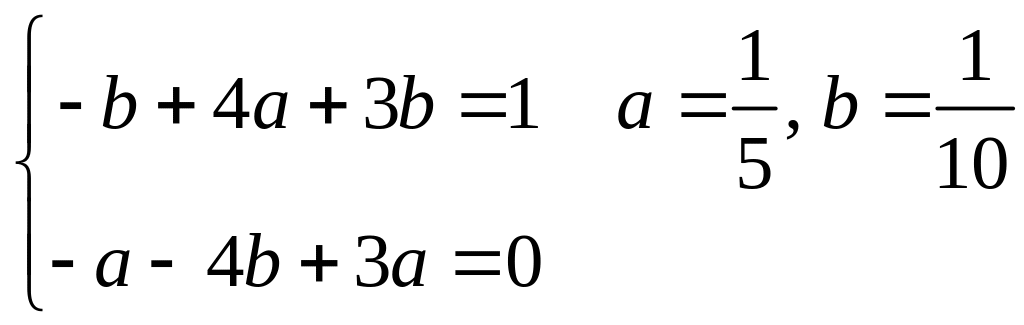
Ответ: .

§12 Линейные уравнения Эйлера

Т.е. ― линейное неоднородное уравнение с особыми .

― важен интервал. Тогда можно разделить на .

Однородное уравнение Эйлера:

Определение: Определяющее уравнение для однородного уравнения

Эйлера ― следующее:

― многочлен степени относительно .

линейного однородного уравнения надо знать фундаментальную систему решений.

Теорема: Для того, чтобы найти фундаментальную систему решений , надо найти корни соответствующего уравнения вместе с их кратностями. Далее каждому корню следует сопоставить функции: , где ― кратность .

Каждой паре комплексных сопряженных корней уравнения следует сопоставить функции

где ― кратность корней .

Фундаментальную систему решений образуют функции, сопоставленные указанным образом всем корням и всем парам корней .

Доказательство: В ― замену ― ? в исходном.

Теперь ― ? Замена возможна, т.к.

.

.

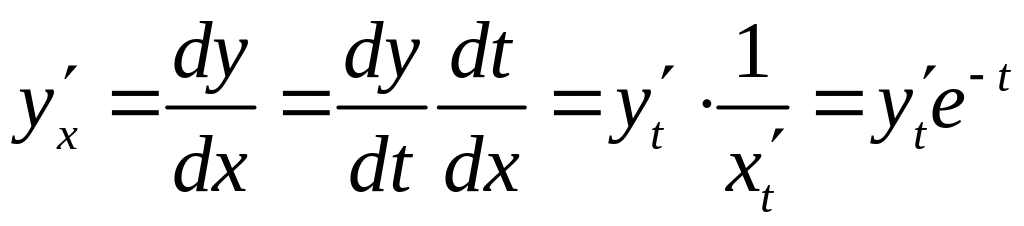
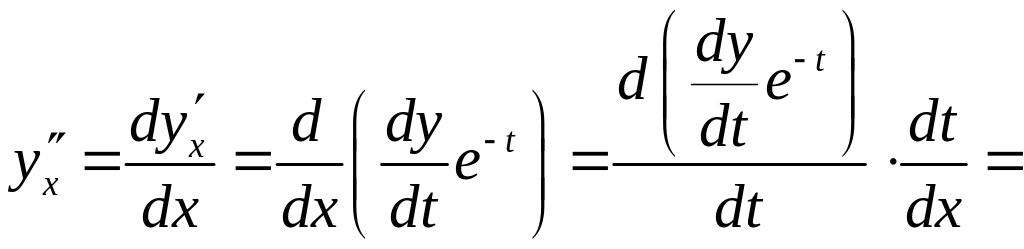
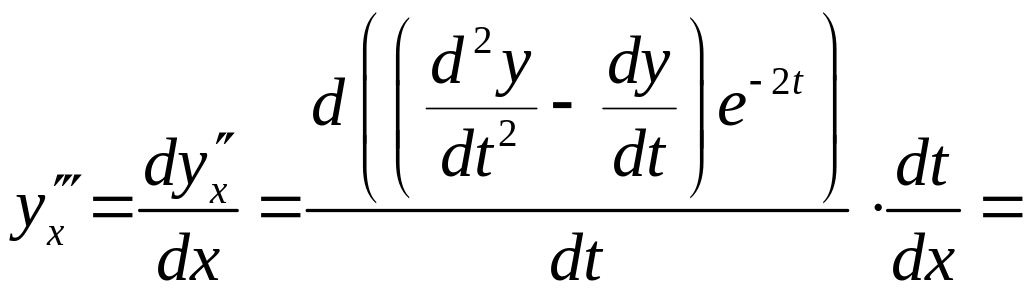
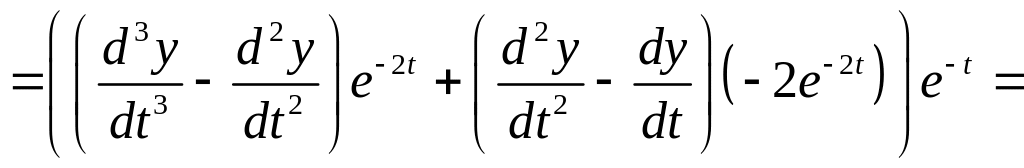
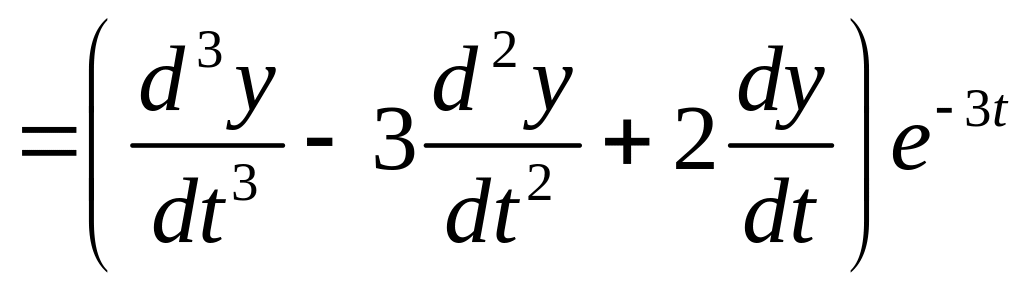Подставляем в :

,

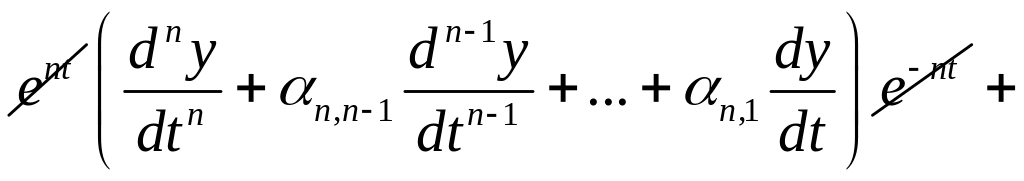
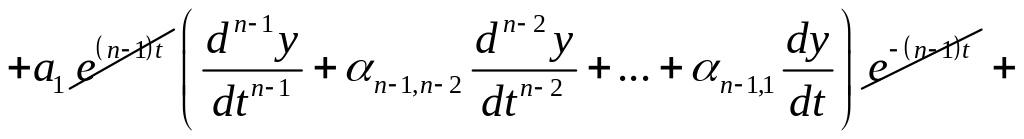
Преобразовали в . ― линейное однородное уравнение с постоянными коэффициентами .

― характеристическое уравнение для

Можно получить, подставив в подставив в :

.

После деления на получается определяющее уравнение . Его смысл: характеристическое уравнение для , записанное по виду уравнения .

После того, как найдем корни и кратность , найдем фундаментальную систему решений . Она будет состоять из функций, зависящих от . Если вернемся к , тогда получим фундаментальную систему решений ; очевидно, получатся функции, участвующие в формулировке теоремы. Ч.т.д.

Пример: ,

Фундаментальная система решений: .

Ответ: .

Для решения неоднородных уравнений Эйлера не существует универсальных методов: либо методом Лагранжа, либо неопределенных коэффициентов ― с соответствующими видоизменениями (сначала заменой ― линейное неоднородное уравнение).