§10 Линейные однородные уравнения.
коэффициенты
уравнения;
непрерывны.
Краткая
запись (1):
.
линейный оператор.
.
Т.к. справа ноль, то уравнение однородное.
Свойства: 1.
решение (1)
Линейная комбинация с любыми коэффициентами любых решений (1) – решение (1).
решение
уравнения (1),
такое,
что
.
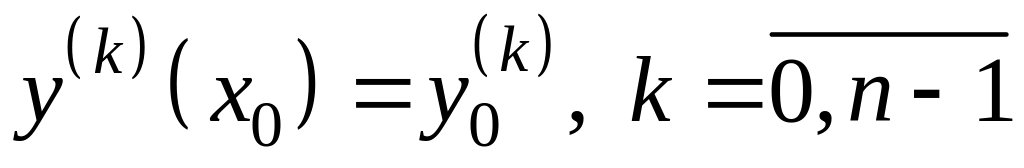Теорема
1:
Пусть
решения
уравнения (1);
Тогда
линейно зависимы.
Доказательство:
Определитель этой системы –
Тогда
существует нетривиальное решение.
Выберем конкретное нетривиальное
решение системы
.
По свойству 2
тоже
решение. Выберем
.
Наше решение в точке
удовлетворяет начальным условиям. С
другой стороны,
тоже удовлетворяет условию
.
По свойству 3
.
Т. к. не все
,
то
линейно зависимы, ЧТД.
Теорема 2. Пусть – решение (1). Тогда справедливо ровно 1 из следующих утверждений:
1.
2.
Доказательство:
Обоснуем, что не может где-то
,
а где-то не равняться.
Пусть
.
Тогда
линейно зависимы, т. е.
линейно независимы.
От
противного. Если бы были линейно зависимы,
то по теореме из предыдущего вопроса
.
Если
бы
то
линейно зависимы.
линейно зависимы.
От противного.
От противного.
Определение: Фундаментальной системой решений (1) называется совокупность его линейно независимых решений.
Теорема 3. Для уравнения (1) существует фундаментальная система решений.
Доказательство:
Возьмем числа
.
Потребуем, чтобы
.
Обозначим
такие решения (1), для которых
.
По свойству 3 с любыми начальными
условиями решение в
существует. Тогда
По теореме 2
линейно независимы, т.е. фундаментальная
система решений.
Замечания:
Общего метода для нахождения фундаментальной системы решений не существует.
Каждое (1) имеет бесконечное количество фундаментальных систем решений.
Частный случай (1): когда
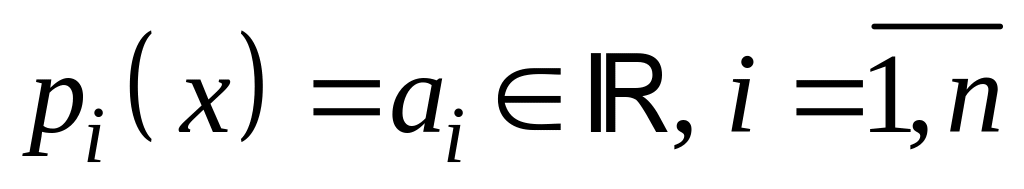– числа
Определение:
Характеристическим уравнением для (2)
называется следующее выражение:
,
где
– характеристический многочлен (2):
.
Свойства (и для любого многочлена):
1.
с точностью до порядка множителей
представление
в виде следующих произведений:
,
где
попарно различные, вообще говоря,
комплексные числа, которые называются
корнями многочлена, а
кратности
корней, причем
степень
многочлена. (Основная теорема алгебры)
2.
кратность
корня
,
причем
3. Два любых комплексно-сопряженных числа одновременно либо не являются корнями , либо являются, причем одинаковой кратности.
Теорема
4.
Фундаментальную систему решений (2)
образуют функции, сопоставленные всем
действительным корням и всем парам
комплексно-сопряженных корней
соответствующих
корням
многочлена, следующим образом:
Если
корень
кратности
,
то ему следует сопоставить
.Если
–
пара комплексно-сопряженных корней
кратности
,
то им следует сопоставить
–
для
–
для
Доказательство:
Функции из формулировки линейно
независимы;
– по свойству 1; т.е. нужных функций
.
Осталось показать, что эти
функций – решения системы (2).
Доказательство проведем для действительных корней . Для комплексных корней доказательство аналогичное.
Рассмотрим
.
Для других функций аналогично.
Теорема
5.
Формула общего решения (1) имеет вид:
(3) где
– произвольные, принадлежащие
числа, а
– фундаментальная система решений.
Доказательство:
Формула (3) ничего, кроме решений (1) не содержит (т.к. линейная комбинация решений линейного уравнения – решение линейного уравнения).
К любому решению (1) из (3) можно придти. Пусть
–
любое конкретное решение (1). Выберем
.
начальное
условие. С такими значениями производных
в точке
существует единственное решение (2)
(т.е.
).
Пусть
– определитель системы, равный (для
фундаментальной системы решений)
Т.е.
решение (относительно
).
Находим нужные
.
Тогда (3) – решения (1) с начальными
условиями в точке
и по соответствующему свойству
,
ЧТД.
Следствие: Уравнение (1) не может иметь больше линейно независимых решений.
Доказательство:
(От противного) Пусть
– линейно независимы (фундаментальная
система решений). Ио теореме 5
.
Тогда
.
Т.к.
,
то
линейно зависимы. Противоречие.
Примеры:
1.
.
;
По теореме 4
– фундаментальная система решений
(ф.с.р.).
Ответ:
2.
.
.
ф.с.р.
Ответ:
3.
(кр.
1)
ф.с.р.
по теореме 4.
Ответ:
4.
ф.с.р
Теорема
6.
Пусть дано
Зная одно нетривиальное решение
уравнения (1), можно подстановкой
понизить порядок уравнения, сохранив
его линейность и неоднородность.
Доказательство:
Уравнения помножим на
чтобы получить (1)
Теорема
7.
–
линейно независимые функции.
.
Тогда
уравнение вида (1), для которого эти
функции являются фундаментальной
системой решений.
Доказательство:
1. Существование.
(4)
[разложение по столбцу]
(4’)
2. Единственность.
Предположим, что существует еще одно уравнение вида (1) с такой ф.с.р.:
;
отлично от (5).
[т.к.
и (5) различны, то хотя бы одна пара
свободных коэффициентов содержит разные
коэффициенты]
.
Вычтем из (1) (5):
(6) – линейное однородное уравнение.
Очевидно, что исходные функции – решения
уравнения (6). Уравнение (6) рассмотрим
на интервале
.
Делим интервал на старший коэффициент:
(7). Порядок (7) –
,
а решений –
.
По теореме 5 линейное однородное уравнение
не может иметь решений больше, чем
порядок. Противоречие.
Теорема 8.
Пусть
–
фундаментальная система решений (1),
тогда справедлива формула:
(формула Остроградского-Лиувилля).
Доказательство:
Из
теоремы 7: по ф.с.р. линейное однородное
уравнение восстанавливается единственным
образом, и это будет уравнение
.
Сопоставляя
и
(1), получим:
.
Далее
воспользуемся формулой для производной
определителя:
.
