§6 Уравнения высших порядков.
― уравнение
порядка
, разрешенные относительно старшей
производной.
Обычно
решение ― совокупность функций, зависящих
от
произвольных постоянных.
.
Общее решение: .
Частное
решение ― общее с конкретными
.
Особое решение ― которое не получается из общего приданием значений константам.
Дополнительные условия:
― начальные
условия.
― задача
Коши
Теорема:
Пусть в некоторой окрестности точки
являются непрерывными функции
.
Тогда в некоторой окрестности точки
единственное решение задачи Коши
.
Далее ― о частных случаях.
или
1)
Ответ:
2)
Предположим,
что в (3)
,
тогда (3) –уравнение в точных производных.
–
не обязательно решается, но лучше тем,
что порядок его на единицу меньше. В
общем случае неизвестно, как находить
.
Пример:
.
3)
Пусть в (3) у
существует свойство:
.
.
Свойство однородности функции
относительно
(
–
степень однородности). Тогда порядок
(3) можно понизить на 1.
Замена:
,
…
-
решается не всегда.
Пример:
– линейное
неоднородное уравнение
…
Ответ:
.
4)
.
Проинтегрировав
раз, получим решение. Но решение для
может быть другим: в неявном виде,
параметрическом виде.
Пример:
-
уравнение с разделяющимися переменными,
…
5)
(или параметрически). Вместо
–
.
§7 Системы дифференциальных уравнений.
уравнений
с
неизвестными.
.
Формы записи:
1.
Нормальная:
(1)
2. Симметричная:
(2)
– система уравнений.
Легко переводятся одна в другую:
из
(2) в (1):
из
(1) в (2):
.
Решение
– совокупность функций, в этой совокупности
присутствуют
производных постоянных:
.
Константы – одни и те же для любых .
Начальные
условия:
(3).
((1) или (2)) и (3) – задача Коши.
Теорема:
Пусть в окрестности точки
существуют и непрерывны
.
Тогда в некоторой окрестности
решение задачи Коши (1), (3).
Метод исключения.
Пример:
;
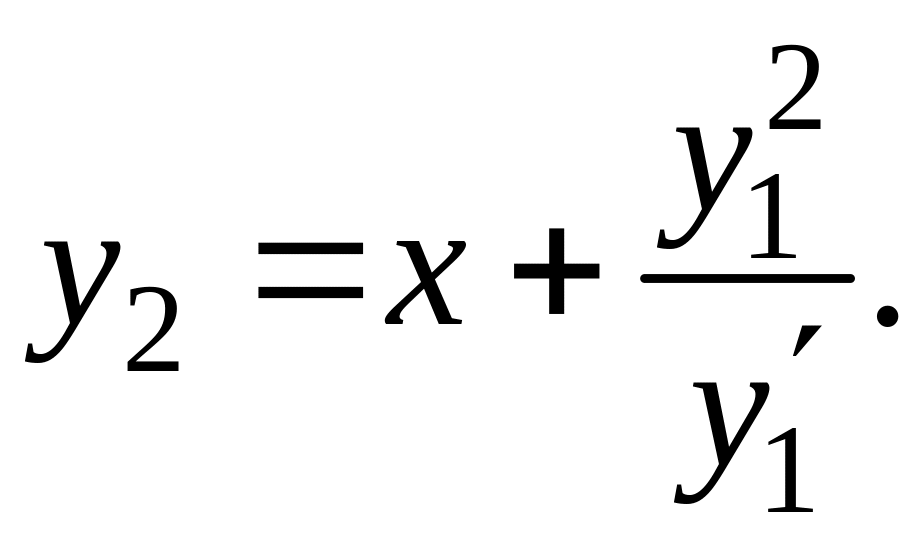Подставляем во второе:
Ответ:
После исключения получаем уравнение большего (n - ого) порядка. Не всегда можем исключать функции. Общий случай для этого метода.
.
Дифференцируем:
Получим
штук равенств, которые связывают
Будем исключать
Выберем
из равенства №1, подставляем во все
остальные равенства. Выбираем
из равенства №2, подставляем во все
остальные.
Получаем дифференциальное уравнение
-го
порядка (будет содержать
).
Определение:
интеграл системы (1) – непрерывная
дифференцируемая функция
,
дифференциал которой, вычисленный в
силу системы (1), тождественно равен
нолю, т. е.
[вычисленный
в силу системы – значит, что
находят из равенств системы (1), т.е.
]=
.
Определение:
Первый интеграл системы (1) – соотношение
,
где
– интеграл системы (1), а
.
Определение:
Интегралы системы (1)
– независимые, если
.
Определение:
Общий интеграл системы (1) – совокупность
его первых интегралов
,
для которых соответствующие интегралы
независимы.
Система (1) считается решенной, если найден её общий интеграл. (Общий интеграл – аналог решения в неявном виде.) Общий интеграл удобно находить для систем в симметричной форме, т. к. тогда удобно использовать свойство равных дробей:
Если
,
то для
.
Пример:
– первый
интеграл системы
.
По
свойству равных дробей;
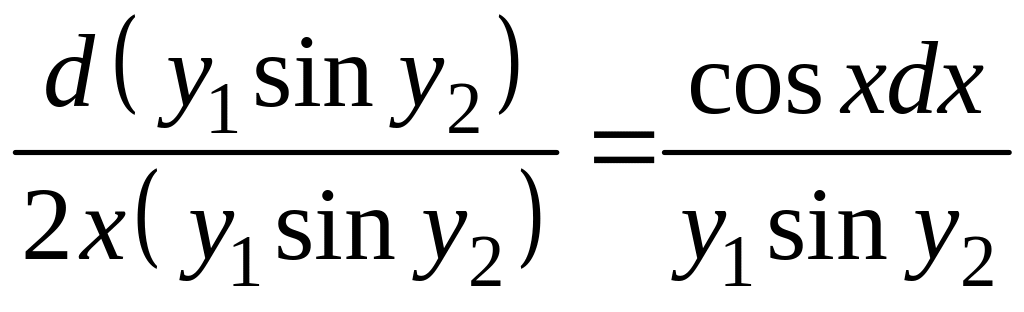
Уравнение
выше можно расценить как уравнение с
разделенными переменными
,
.
После интегрирования:
.
Ответ:
