Белорусский Государственный Университет

Факультет Радиофизики и Электроники

А.П.Шилин

Дифференциальные уравнения

Конспект лекций

Минск 2005

Набор и верстка:

Р.А.Федоров

А.В.Кудько

Конспект:

В.В.Баранов

Дифференциальные уравнения\

§1 Основные понятия и некоторые факты.

Определение: Обыкновенное дифференциальное уравнение порядка ―уравнение вида ,

в котором ―независимая переменная, ―искомая функция, ―заданная функция.

Кроме обыкновенных дифференциальных уравнений, дифференциальное уравнение в частных производных: для функций нескольких переменных. (Для ―обыкновенная производная).

Пример: , .

Дифференциальное уравнение -го порядка ― лишь бы была (а все остальное может отсутствовать)

Системы дифференциальных уравнений.

Решить: найти все решения (либо доказать, что их нет).

Решение ― объект, который при подстановке обращает уравнение в истинное

Пусть ―решение дифференциальное уравнение : .

Задача о радиоактивном распаде.

―время, ―масса вещества. .

Задача о гармонических колебаниях

― уравнение 1-го порядка, разрешенное относительно производной

Определение: Решение дифференциального уравнения получено в квадратурах, если оно выражено через элементарные функции посредством конечного числа арифметических операций, операций образования сложной функции и несобственных интегралов, при этом решение может быть функцией, заданной явно, неявно, параметрически, а неопределенные интегралы могут быть неберущимися.

(обычно решить ― решить в квадратурах)

― разные формы записи

. Теперь неизвестна.

Для решения в квадратурах менять ролями переменные в дифференциальных уравнениях можно (получается неявная функция)

Определение: Начальное условие для уравнения ―следующее дополнительное условие для его решения: , где ―заданные числа

Определение: и ―задача Коши (решить дифференциальные уравнения с начальными условиями).

Наиболее типично: у задачи Коши единственное решение (но не всегда).

Теорема: Пусть в прямоугольнике является непрерывной функцией .

Пусть , где такое дифференциальное уравнение, что . Тогда по меньшей мере на отрезке единственное решение задачи Коши . [Без доказательства]

формулы для приближенного решения задачи Коши (в общем случае точной формулы не существует):

, где ―такое число, для которого в прямоугольнике П .

.

Пример: не решается в квадратурах (это доказано)

Задача Коши:

§2 Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.

1. уравнение с разделенными переменными:

Пример:

2. уравнение с разделяющимися переменными:

(следить за пропажей корней)

Пример: ,

-подходит

Ответ:

3. уравнение вида

―новая функция, зависящая от

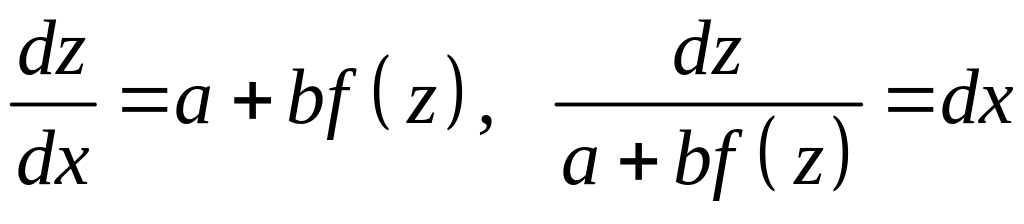
Пример:

( ―решение)

Ответ: .

4) однородное уравнение:

5) уравнение вида .

единственное решение: ―решение (*)???

.

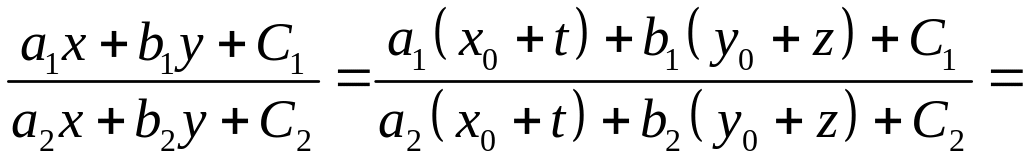
§3 Уравнение полных дифференциалов и интегрирующий множитель.

―предположим, что эти функции определены и непрерывно дифференцируемы в некоторой односвязной области (нет дырок)

Определение: Уравнение называется уравнением полных дифференциалов, если такая, что .

Уравнение можно записать в виде: ―решение .

Теорема: Для того чтобы , для того чтобы , необходимо и достаточно, чтобы

Из этих рассуждений видно, что решение задачи с уравнением полных дифференциалов сводится к нахождению .

Пример:

Проверим, что уравнение ― полный дифференциал.

― верно.

;

.

[ , но она включена в ].

Ответ: .

Предположим, что уравнение ―не уравнение полных дифференциалов

Определение: Интегрирующим множителем для уравнения назовем , после умножения на которую уравнение становится полным дифференциалом.

Общего метода для нахождения интегрируемого множителя нет. Существуют различные методы:

1)

― тогда ― интегрирующий множитель.

,

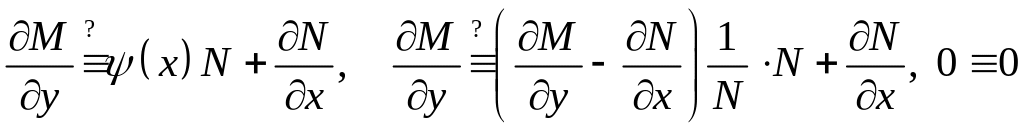
Мы доказали справедливость формулы для интегрирующего множителя для конкретного случая.

2) ,

Под интегралом понимается конкретная первообразная.

3)

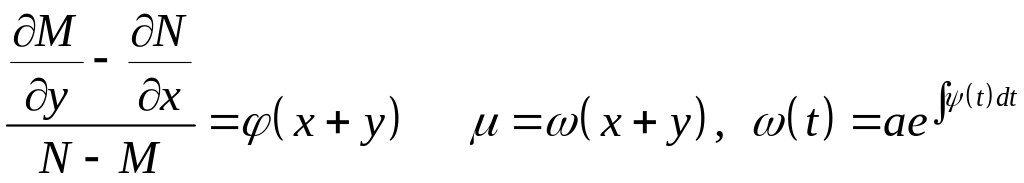
? ?(*)―см. курс матана, сем.№2, КРИ-2.

(*)―часть теоремы о независимости КРИ-2 от пути интегрирования, а ―подынтегральное выражение для КРИ-2 (правда, в нем должны конкретные пределы).

Если ―полный дифференциал, то КРИ-2 не зависит от пути интегрирования.

можно искать по линиям, , 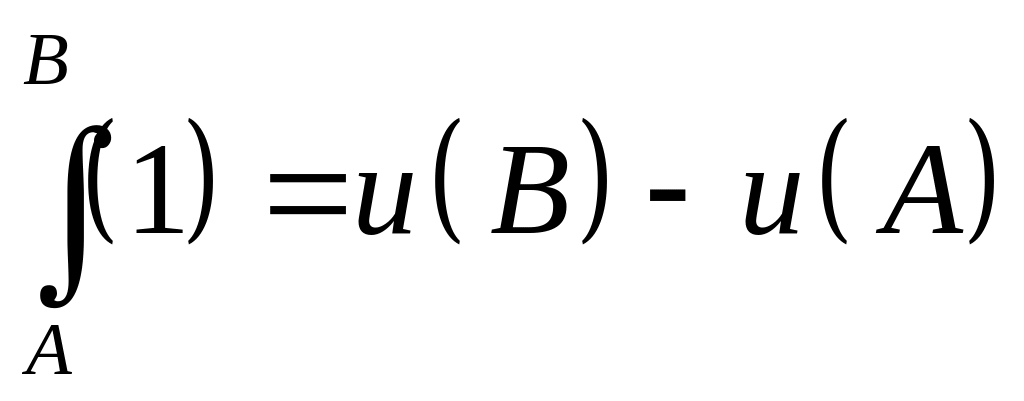. Тогда

Или:

З адача

В ― источник света. Найти форму кривой, отражаясь от которой лучи . ― равнобедренный .

(можно решать по-разному).

.

.

Интегрирующий множитель: .

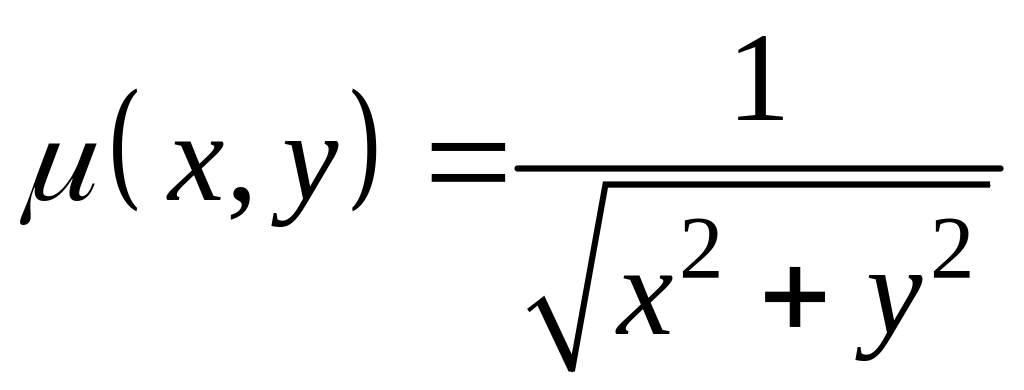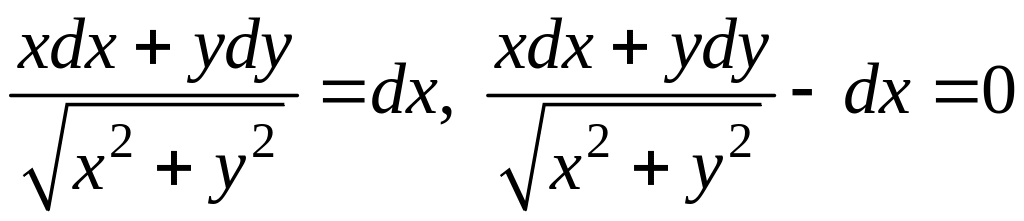― уравнения в полных дифференциалах

.

― семейство парабол.