13.Нахождение частного решения неоднородного уравнения методом неопределённых коэффициентов.
1.
(14),
где Rm(x)
полином степени m
с вещественными или комплексными
коэффициентами, а – постоянное
вещественное или комплексное или равное
нулю число.
Случай 1.1:
P(a)≠0
В этом случае частное решение y1 уравнения L[y] = 0 (1) следует искать в виде:
, где
(15)
,
где
(16)
Распишем левую часть (16), используя свойства оператора L подробнее
(17)
Сокращая
на
и сравнивая коэффициенты при одинаковых
степенях
,
получаем:
: 
: 
… (18)
: 
Так как P(a) ≠ 0, все qi находятся из (18) последовательно единственным образом.
Случай 1.2:
«а» является корнем характеристического многочлена кратности k, т.е. P (a) = 0, P/ (a) = 0, …, P( k-1) (a) = 0, P( k) (a) ≠ 0.
Тогда
частное решение ищется в виде
(19)
Доказательство аналогично случаю 1.
2.
(20)
-
заданные полиномы от
степени равной или меньшей m,
причём хоть один из них имеет степень
m.
Заменяя 
,
(21)
2. сводится к случаю 1.
Используем результаты случая 1.
Случай 2.1:
Число не является корнем характеристического уравнения. Тогда частное решение имеет вид:
(22)
где
–полиномы степени m
с неопределёнными коэффициентами,
которые определяются единственным
образом.
Случай 2.2:
Число является корнем характеристического уравнения кратности k (k≥1). Тогда частное решение имеет вид:
(23)
где –полиномы степени m с неопределёнными коэффициентами, которые определяются единственным образом.
Пример 1:
,
– характеристическое
уравнение,
– общее
решение однородного уравнения.
Случай ?.?:
а =1 не является корнем характеристического уравнения. Тогда частное решение имеет вид:
,
Подставляя
значения
и
в
уравнение и сокращая на e
x
,
получаем: 
.
Откуда
. 
.
–общее
решение данного уравнения.
Пример :
,
,
,
– общее
решение однородного уравнения.
1)
не является корнем характеристического
уравнения.
Тогда 
2) 
,
является корнем характеристического
уравнения.
Тогда 
Подставляя
значения
и
в
уравнение
,
получаем:
,
,
такой член называется вековым.
ЛЕКЦИЯ 5:
14. Приведение однородного линейного уравнения n-го порядка к уравнению с постоянными коэффициентами при помощи замены независимой переменной.
Рассмотрим линейное однородное уравнение (1).
Сделаем
замену независимой переменной
:
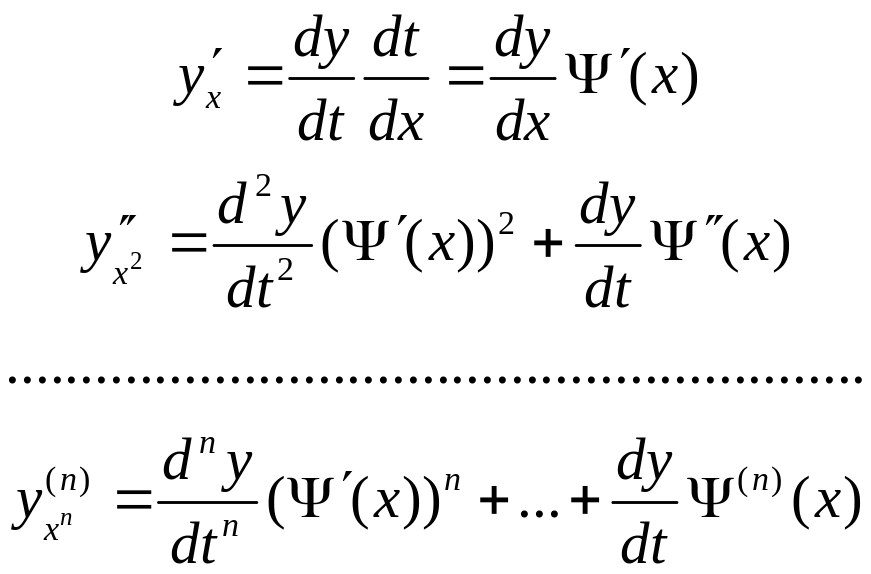(2)
Подставим
(2) в (1) и разделим на
,
получим :
(3).
Необходимо,
чтобы
(4), следовательно:
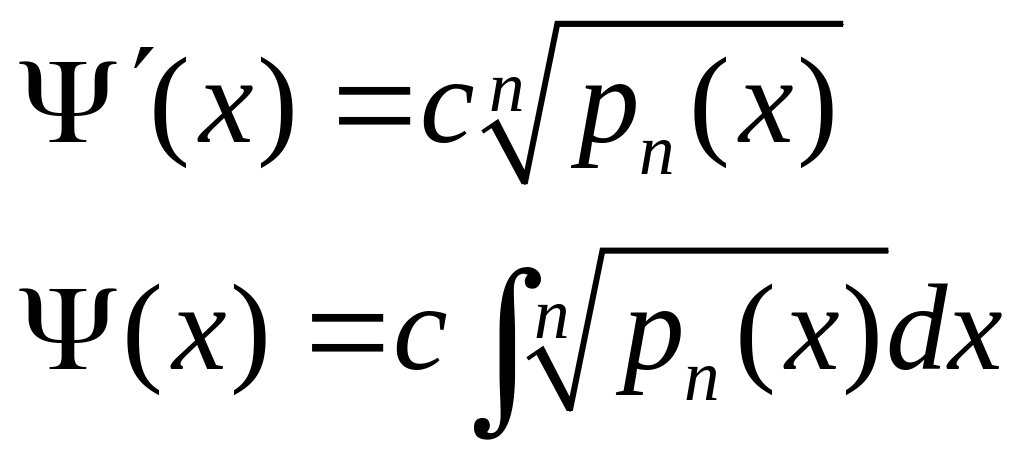(5).
Пример. Уравнение Чебышева.
-
особые точки уравнения ,
.
Построим
общее решение уравнения Чебышев при
(7).
Возьмём
,
тогда
;
(8)
Подставляя (8) в уравнение Чебышева (6), получаем:
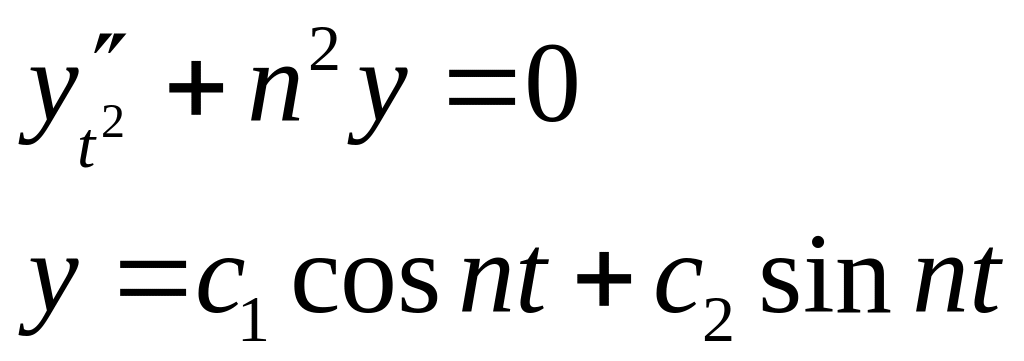
(9)
– общее решение уравнения (6)
15. Линейное уравнение Эйлера.
(1)
х=0 – особая точка уравнения (1)
Решение
этого уравнения существует и единственно
при
.
Будем
рассматривать уравнение (1) при
.
.
Поэтому, согласно №14 :
(2) ,
.
или
(3).
Тогда
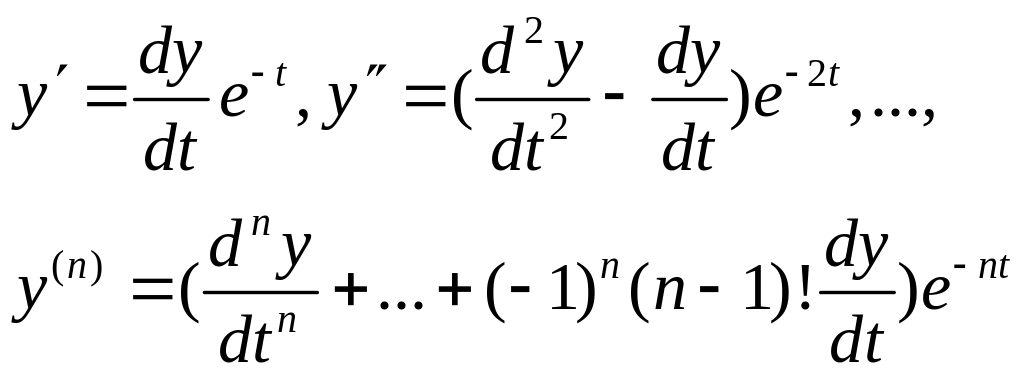(4).
Подставляя (4) в уравнение (1), получаем однородное линейное уравнение n-го порядка с постоянными коэффициентами. Найдя общее решение и полагая в нём , мы получим общее решение уравнения Эйлера.
Пример
1. 
.
-
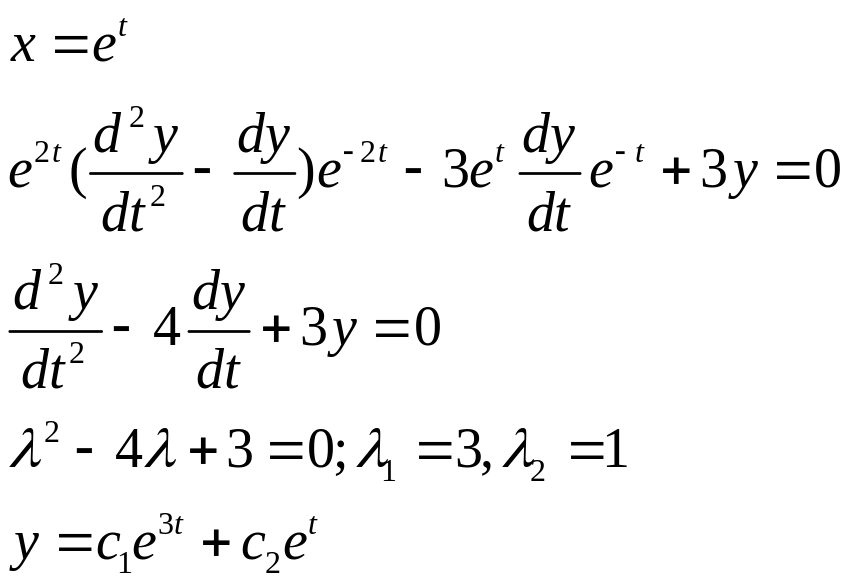
общее решение однородного уравнения
Эйлера.
Пример
2. 
-
общее решение уравнения Эйлера.