11. Метод Коши.
Укажем ещё один способ построения частного решения уравнения (1).
Пусть {zi} i=1,2..n – ФСР уравнения L[y]=0 (2)
(3) – общее решение уравнения (2).
Построим решение уравнения (2), удовлетворяющее следующим начальным условиям :
z = 0, z/ = 0, …, z( n-2) =0, z( n-1) =1 при x = , где a,b, x(a,b).
Это
решение
(5)
Причём
,
,
…,
,
,
где
, (6)
Докажем, что функция
, (7)
где x0 (a,b).
является частным решением уравнения (1) с нулевыми начальными условиями, т.е. Y = 0, Y/ = 0, …, Y( n-1) =0, при x = x0.
Найдём значения производных функции Y(x):
,
первое слагаемое = 0,
,
первое слагаемое = 0, …… (8)
,
первое слагаемое = 0,
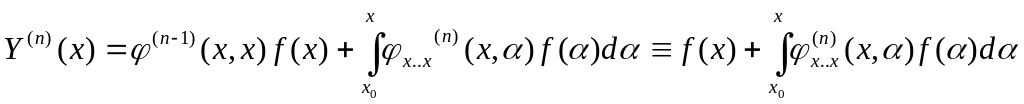и
,
Подставим выражение (8) в уравнение (1):
+……
…+
(9)
или
,
Получим тождество для x, x0 a,b
Итак, , x a,b
(7) –называется
формулой Коши для неодноролного
уравнения.
Очевидно, что Y(x0) = 0, Y/ (x0)= 0, …, Y( n-1) (x0)=0.
Таким
образом 
.
Пример:
– общее
решение однородного уравнения.
Найдём (x,)
z=0, z/=1 при x = .
– oбщeе решение неоднородного уравнения.
ЛЕКЦИЯ 4:
12. Линейные уравнения n-го порядка с постоянными коэффициентами.
, (1)
a1,
a2,
…, an
– постоянные
вещевтвенные числа,
непрерывная
в интервале (a,b).
Рассмотрим
сначала соответствующие уравнению (1)
уравнение
(2),
(2)
Будем искать уравнение (2), следуя Эйлеру, в виде
(3),
(4)
Подставляя (4) в уравнение (2), получим
или
(4)
Таким образом получаем
(5)
– называется характеристическим многочленом или характеристическим уравнением.
Случай 1:
Все корни характеристического многочлена 1, 2, …, n различны и вещественны.
Каждому корню i соответствует частное решение
(i=1..n)
–
линейно
независимая система функций, т.е. ФСР.
(6)
– общее
решение уравнения
.
Пример:
,
,
– общее
решение данного уравнения.
Случай 2:
Среди
корней
характеристического уравнения
есть комплексный корень
Пусть
,
тогда
,
3, 4, …, n – различные и вещественные корни.
(формула
Эйлера)
– комплексная
функция действительной переменной.
Тогда –
,
– также
являются решениями уравнения.
Очевидно, что сопряжённый корень не порождает новых решений.
Таким образом, ФСР в данном случае
,
,
и общее решение имеет вид:
Пример:
,
– характеристическое
уравнение,
,
,
,
– общее
решение.
Случай 3:
Среди корней характеристического уравнения есть кратный действительный корень.
Пусть
– корень кратности k.
P(λ1) = 0, P/ (λ1)= 0, …, P( k-1) (λ1)=0, P( k) (λ1)≠0.
Запишем
полученное ранее выражение
(4) и продифференцируем его по λ m
раз, используя для правой части формулу
Ньютона-Лейбница, а для левой свойства
оператора L.
.
(9)
(10)
Подставим в уравнение (10) λ = λ1 и используем, что
P(λ1) = 0, P/ (λ1)= 0, …, P( k-1) (λ1)=0.
Получим, что
– решение
уравнения (10) при m
= 0, 1,…, (k-1).
,
,…,
,
,…
– ФСР.
(11)
(11) – общее решение уравнения (2).
Пример:
,
– характеристическое
уравнение,
,
,
,
– общее
решение.
Случай 4:
Характеристическое уравнение имеет комплексный корень кратности k. Тогда оно имеет и сопряжённый комплексный корень. Таким образом, для построения ФСР нужно 2k линейно независимых решений, соответствующих этим кратным сопряжённым комплексным корням.
Отделяя вещественные и мнимые части комплексных решений
,
,
… ,
, получим
,
,
… ,
(12)
,
,
… ,
.
Таким
образом, каждой паре сопряжённых
комплексных чисел
кратности k
соответствует 2k
линейно независимых решений вида (12).
И общее решение имеет вид:
(13)
Пример:
,
– комплексные решения.
Отделяя вещественные и мнимые части комплексных решений, получим:
– ФСР
– общее
решение данного уравнения.