7. Построение однородного линейного уравнения, имеющего заданную фср.

Покажем, что всякой системе n непрерывно дифференцируемых и линейно независимых в интервале (a,b) функций y₁,..., y_n, вронскиан которых отличен от нуля в интервале (a,b), соответствует лишь одно уравнение L[y] = 0, для которого эта система функций будет фундаментальной.

Итак, даны y₁,..., y_n. Найти .

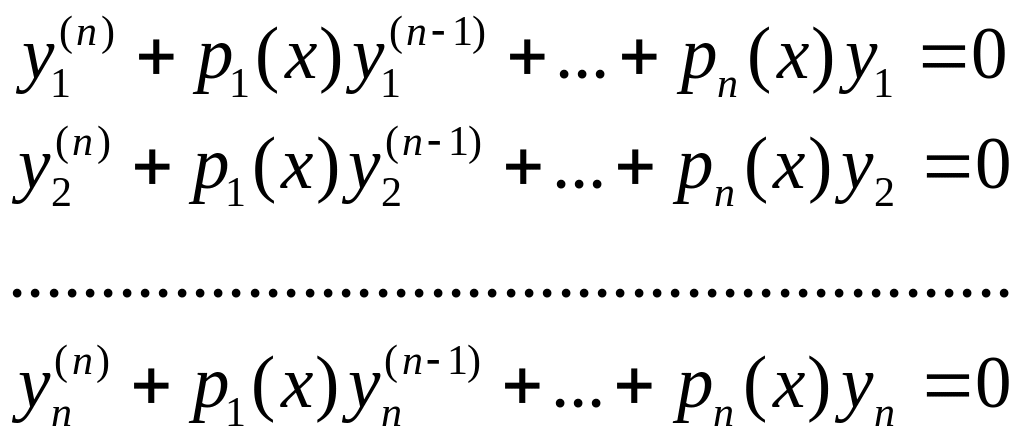(1)

Система (1) решается единственным образом, так как является линейной, неоднородной относительно неизвестных , определитель которой W(x)≠0 в интервале (a,b).

Можно добавить к системе (1) ещё одно уравнение, а именно (2).

Потребуем, чтобы новая система была совместна:

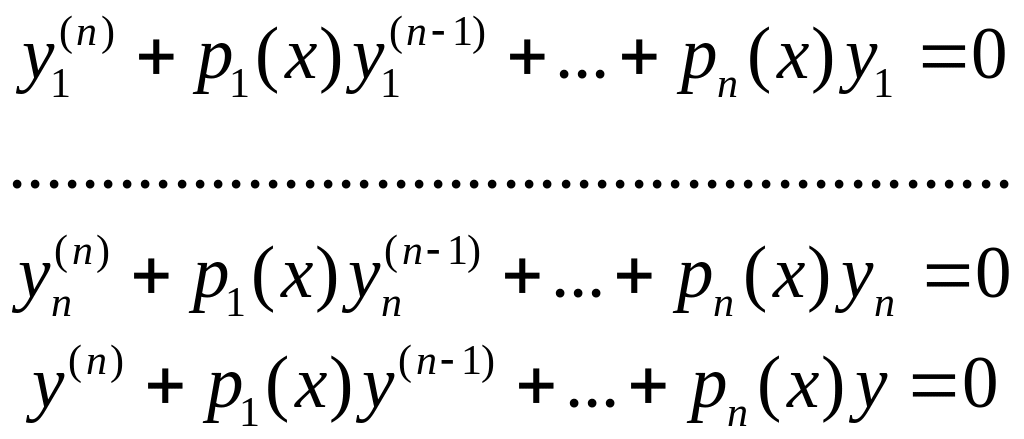(3).

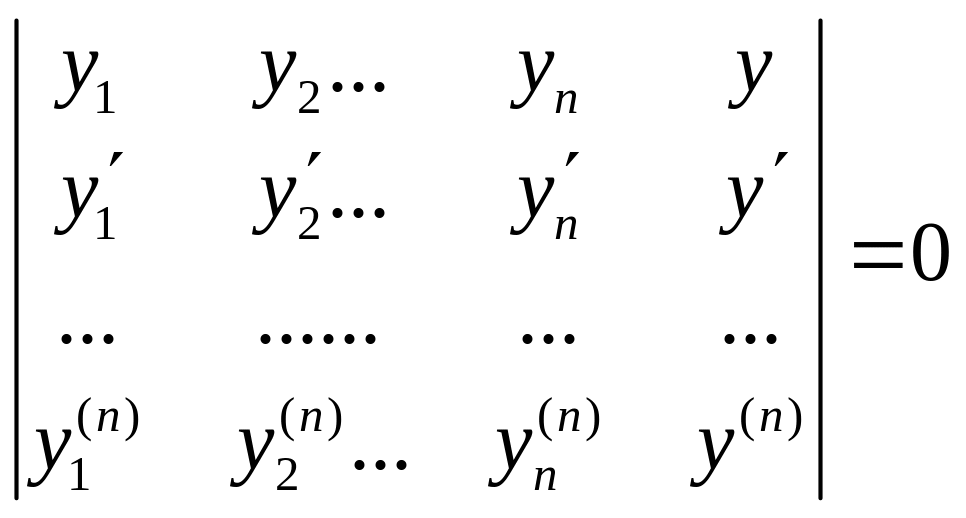Тогда (4), или (5).

Разлагая определитель (5) по элементам последнего столбца и деля все члены на W(x), мы получим искомое уравнение.

Пример.

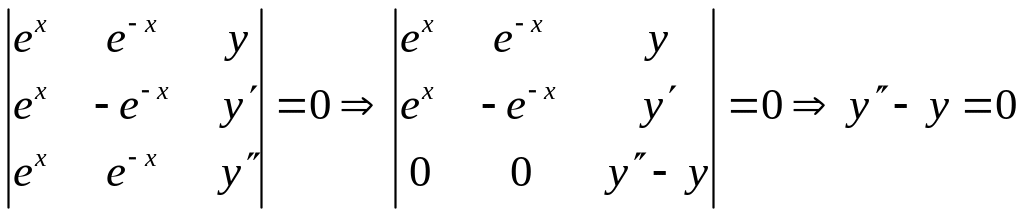
ЛЕКЦИЯ 3:

8. Понижение порядка однородного линейного уравнения.

Знание одного частного решения уравнения L[y]=0 позволяет понизить порядок уравнения на единицу.

y₁ – частное решение уравнения L[y]=0.

Введём новую неизвестную функцию U по формуле:

(1)

(2)

……

Подставляя формулы (1), (2) в уравнение L[y]=0, получим:

(3)

(4)

Коэффициенты этого уравнения непрерывны в интервале (a,b), за исключением точек, где у₁ обращается в нуль.

Решая уравнение (4), находим ФСР – U₁, U₂, …, U_n.

Тогда уравнение L[y]=0 имеет решения

, , , … , (5)

Покажем, что решения (5) являются ФСР для уравнения L[y]=0. Предположим, что решения (5) зависимы. Тогда существует соотношение:

₁ +₂ +…+ ₃ =0 (6)

Сокращая на у₁ и дифференцируя, получим:

₁ U₁ + ₂ U₂ + …+ _n U_n=0 (7)

что противоречит линейной независимости U₁, U₂, …, U_n.

Если известно k линейно независимых частных решений уравнения L[y]=0, то порядок этого уравнения можно понизить k на единиц.

9. Линейное неоднородное уравнение n-ого порядка.

(1)

и непрерывны в интервале (a,b).

Введем новую неизвестную функцию z по формуле y = y₁ + z, где у₁ – частное решение уравнения (1), т.е.

 (2)

Общее решение уравнения (2) даётся формулой:

, где z₁, z₂, …, z_n – ФСР уравнения (2),

а C₁, C₂, …, C_n – произвольные постоянные.

Таким образом,

(3)

Эта формула представляет общее решение уравнения (1) в области (a,b), |y|, |y^|, …, |y^{( n-1)}|.

Замечание 1:

Если правая часть уравнения (1) представляет собой сумму n слагаемых, т.е. , и если для i=1,2..n, то y = y₁ + y₂ +…+ y_n есть частное решение уравнения

.

Замечание 2:

Если известно m частных решений неоднородного уравнения (1)

y₁, y₂,…, y_m, то соответствующее однородное уравнение имеет m-1 частных решений z_k = y_k – y₁, k=2,3…m. Если эти решения линейно независимы в (a,b), то порядок соответствующего однородного уравнения можно понизить на m-1 единиц.

10. Метод вариации произвольных постоянных (метод Лагранжа).

Теорема:

Общее решение неоднородного уравнения (1) можно найти в квадратурах, если известно общее решение соответствующего однородного уравнения (2)

 Будем искать общее решение уравнения (1) в виде (3), где {z_i} i=1,2..n – ФСР уравнения (2).

Найдём производные выражения (3), подчиняя их n-1 условиям:

, второе слагаемое равно нулю,

, второе слагаемое равно нулю,

…… (4)

, второе слагаемое равно нулю,

Подставляя (3) и (4) в уравнение (1), получим:

(5)

Так как , то окончательно получим

(6)

Итак, для определения С_i(x) получаем следующую систему из n дифференциальных уравнений:

,

,

…… (7)

Система (7) является линейной неоднородной относительно С_i ^/ (x) с определителем равным W(x)0 в интервале (a,b).

Решая систему (4) по правилу Крамера получаем:

, i=1,2…n; (8)

где W_{n i} – алгебраические дополнения к элементам n–ой строки определителя W(x).

Из , i=1,2…n; (9)

где C_i– произвольные постоянные, а  x₀  (a,b).

Подставляем (9) в выражение (3), получим:

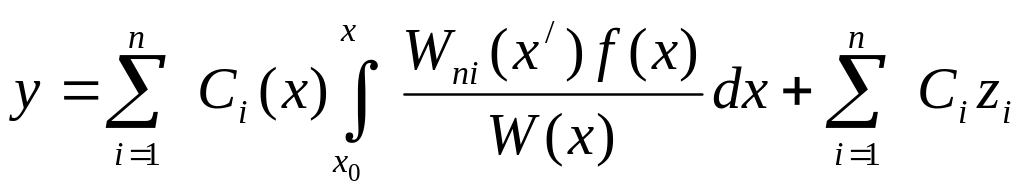, (10)

Пример:

– общее решение однородного уравнения.

Решение неоднородного уравнения ищем в виде:

Составим систему для нахождения и :

 ,

.

.