41. Уравнение Эйлера.

Исследуем на экстремум функционал

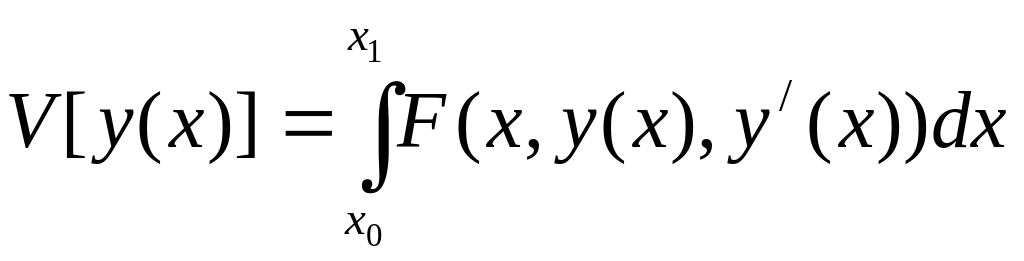(1)

трижды дифференцируема.

Предположим, что экстремум функционалом достигается не дважды дифференцируемой кривой .

(2)

при получим кривую ,

при получим кривую , где вариация функции .

и аналогично

и так далее.

Тогда (3) содержит при кривую, на которой достигается экстремум, а при некоторую близкую допустимую кривую.

Будем рассматривать значение функционала 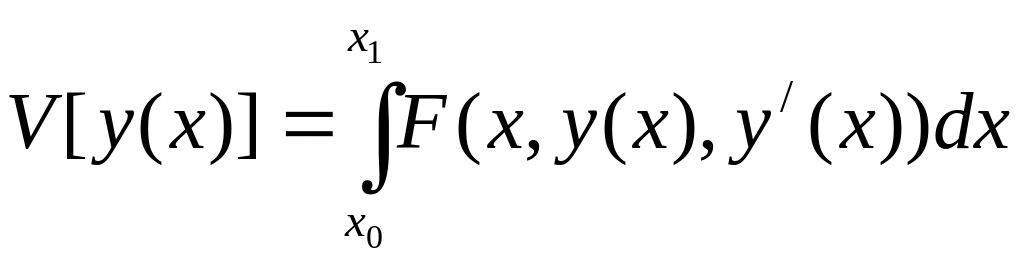на кривых семейства

Функционал превращается в функцию от , т.е. .

Эта функция достигает экстремума при . Необходимое условие этого .

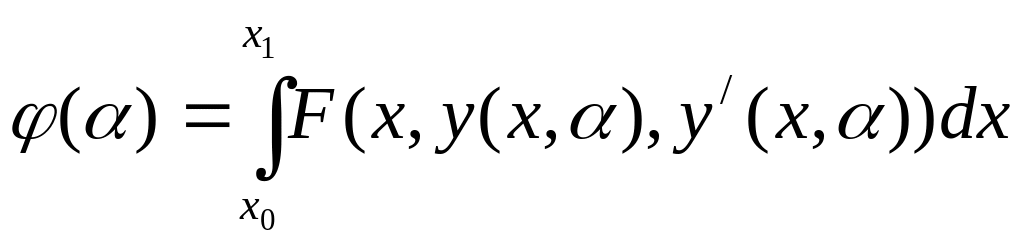(4)

Найдём :

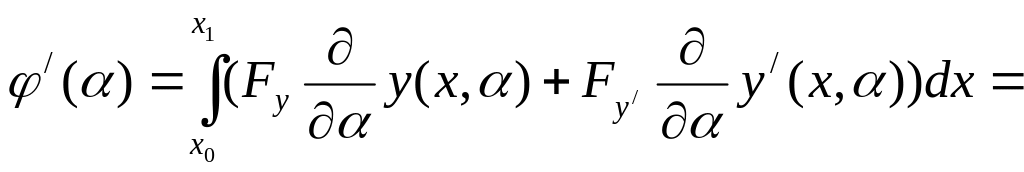
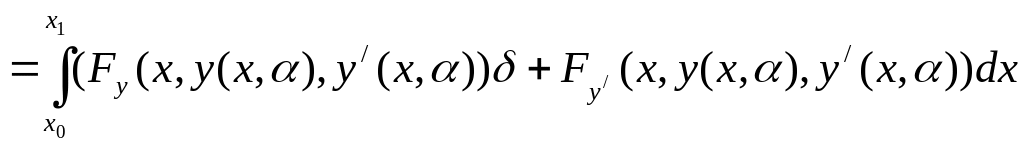
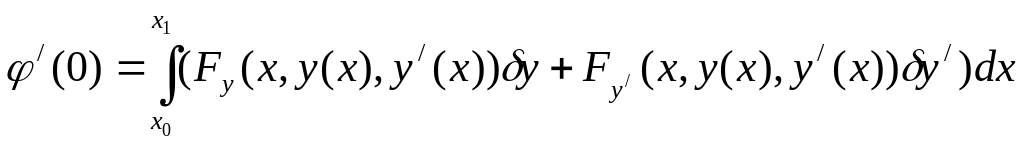(5)

является вариацией функционала и необходимое условие экстремума функционала является условие .

Итак, 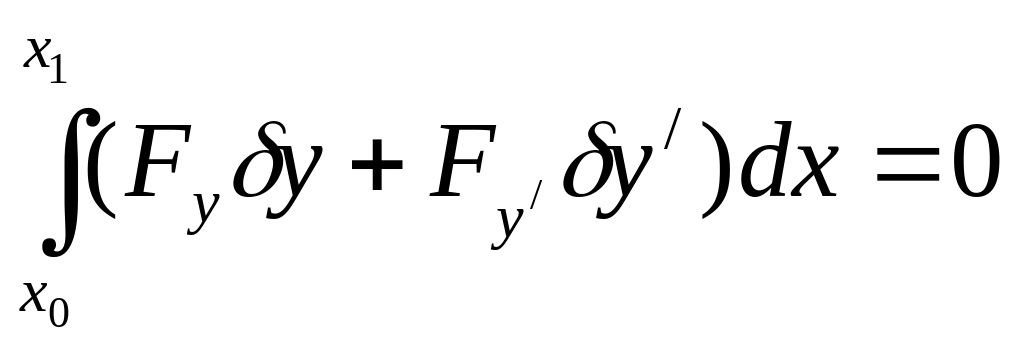(5^/)

Интегрируя второе слагаемое по частям, получим:

, так как

,

.

Все допустимые кривые проходят через фиксированные граничные точки.

(6)

Применяя основную лемму вариационного исчисления к интегралу (6), где произвольная функция, а непрерывная функция, получим, что или в развёрнутом виде:

(7)

Это уравнение называется уравнением Эйлера, а интегральные кривые уравнения Эйлера называются экстремалями.

Только на экстремалях может достигаться экстремум функционала .

С₁ и С₂ находим из условий _, .

Это только необходимое условие достижения экстремума.

Замечание:

Краевая задача не всегда имеет решение, или оно не единственно.

Пример: Задача о брахистохроне.

Определить кривую, соединяющую точки А и В, при движении по которой материальная точка скатится из точки А в точку В в кратчайшее время? (трением и сопротивлением среды пренебречь).

Поместим начало координат в точку А, а ось направим горизонтально, ось 0у – вертикально вниз. Скорость движения материальной точки .

Тогда ; , .

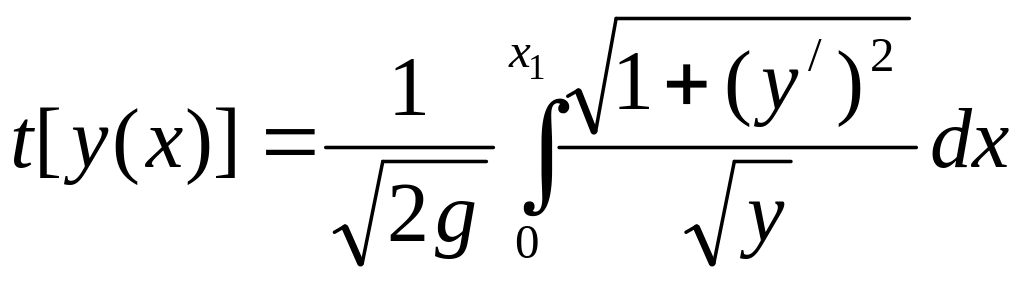Уравнение Эйлера для данного функционала имеет вид:

или

или

.

Введём параметр , полагая, что .

Тогда ,

_,

_,

обозначим , , так как ,

_,

где радиус катящегося круга, который определяется из условия прохождения циклоиды через точку . Брохистохроной является циклоида.