36. Интегральное уравнение Фредгольма 2-го рода с вырожденным ядром.
(1),
где
(2).
-
линейно независимы попарно между собой.
(3).
Обозначим
(4), тогда:
(5). Здесь (k=
= 1,2,...,n).
Пусть
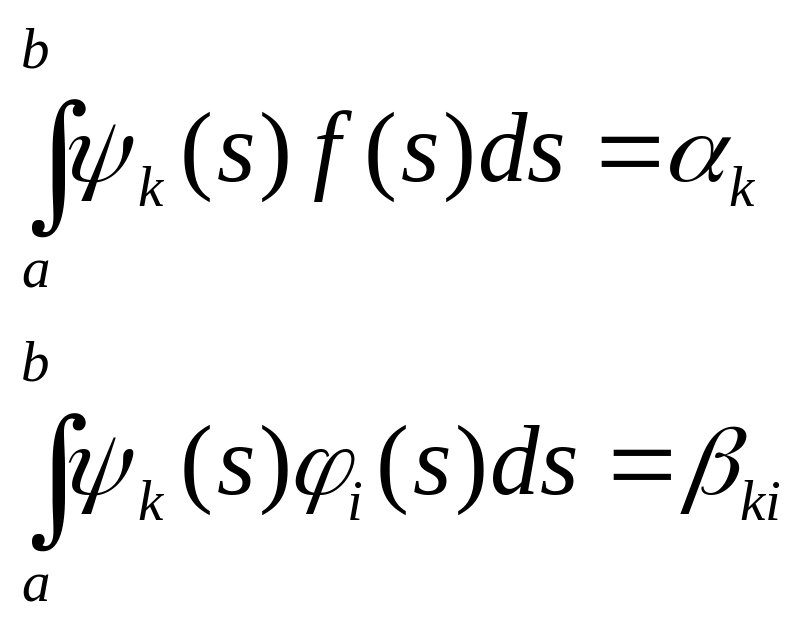(6), 
,
(k
= 1,2,...,n)
(7).
Определитель системы (7) имеет вид:
(8).
Отметим,
что
.
Следовательно,
для достаточно малых значений
существует
единственное решение.
-
многочлен от λ степени n,
имеет не более n
различных корней.
Корни
уравнения
называются характеристическими числами
ядра k(t,s).
Если
уравнение однородное, т.е. f(t)=0,
или
,
то
корень
является собственным значением
однородного уравнения.
Для
неоднородного уравнения при
возможны два случая: существует либо
бесконечное множество решений, либо ни
одного.
37. Теорема Фредгольма для уравнения (1).
Если λ не является характеристическим (собственным) числом, то интегральное уравнение (1) имеет единственное решение при любом свободном члене f(t).
Это первая теорема Фредгольма для уравнения (1).
(9)
называется присоединённым или союзным
к однородному уравнению
.
Вторая теорема Фредгольма.
Если λ является собственным числом интегрального уравнения и этому числу соответствует k линейно независимых решений однородного уравнения (1) {f(t)=0}, то союзное уравнение (9) имеет столько же, т.е. k, линейно независимых решений.
Для
определения
получают систему, сопряжённую с системой
(7). Эти системы имеют одинаковое число
линейно независимых решений.
Третья теорема Фредгольма.
Неоднородное интегральное уравнение с вырожденным ядром (1) при собственном значении λ будет разрешаемо тогда и только тогда, когда свободный член f(t) будет ортогонален ко всем решениям союзного однородного уравнения (9).
Т.е.
,
(k
= 1,2,...,n),
где
-
решения союзного уравнения (9).
Пример. 
Обозначим:
.
ЛЕКЦИЯ 14:
38. Вариационное исчисление. Метод вариации в задачах с неподвижными границами.
В задачах физики иногда возникает необходимость найти максимальные и минимальные значения величин, которые зависят от одной или нескольких функций.
Определение 1:
Функционалом
называют переменную величину
,
зависящую от функции
,
если
из некоторого класса функций соответствует
значение
,
т.е. имеет место соответствие: функции
соответствует число
.
Аналогично определяются и функционалы, зависящие от нескольких функций или зависящие от функций нескольких независимых переменных.
Простейшим
примером является длина
дуги
кривой, соединяющей две заданные точки
и
.
Площадь
некоторой поверхности также является
функционалом, так как она определяется
выбором
:
,
где
проекция
поверхности на плоскость
.
Моменты инерции, статические моменты, координаты центра тяжести некоторой однородной кривой или поверхности также являются функционалами, так как определяются выбором функций, которые определяют кривые или поверхности.
Вариационное исчисление изучает методы, которые позволяют находить максимальные и минимальные значения функционалов.
На развитие вариационного исчисления как самостоятельной математической дисциплины оказали влияние три задачи:
Задача о брахистохроне: задача о линии наибыстрейшего ската, которая называется брахистохроной (Иоганн Бернулли, 1689). Эта линия, соединяющая две заданные точки, не лежащие на одной вертикальной прямой, и по которой материальная точка скатится за кратчайшее время. Оказалось, что линией быстрейшего ската является циклоида.
Задача о геодезических линиях.
Найти
линию наименьшей длины, соединяющая
две заданные точки на некоторой
поверхности
.
Такие линии называются геодезическими.
Найдём минимум функционала:
,
где
и
удовлетворяют условию
.
Изопериметрическая задача:
Требуется найти линию заданной длины, ограничивающую максимальную площадь .
Чаще всего рассматривают следующие основные вариационные задачи:
,
,
,
.
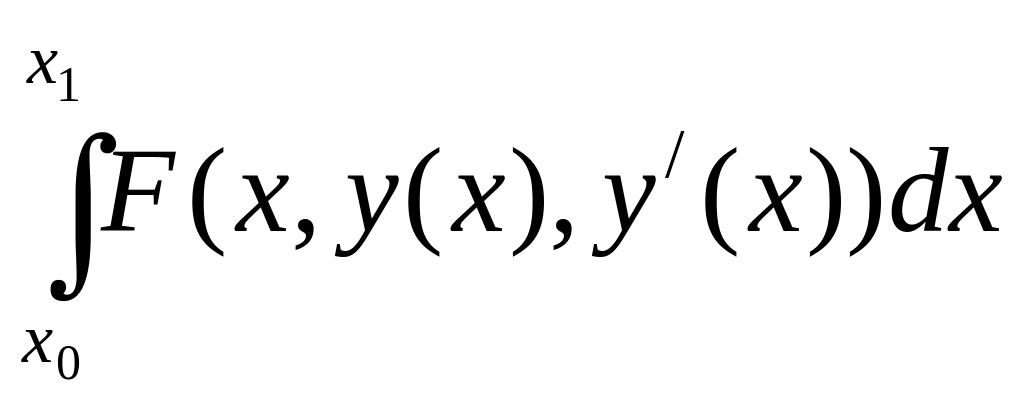
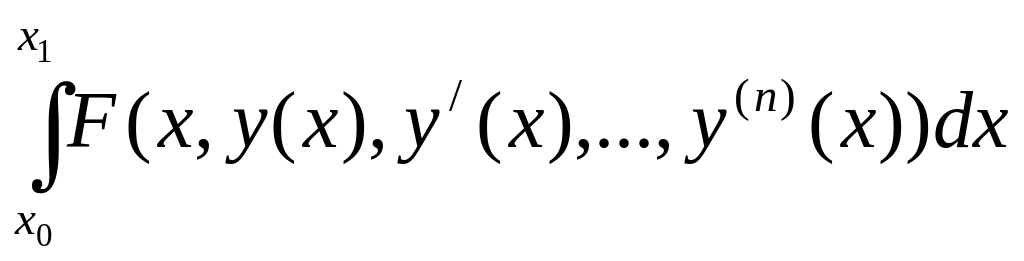
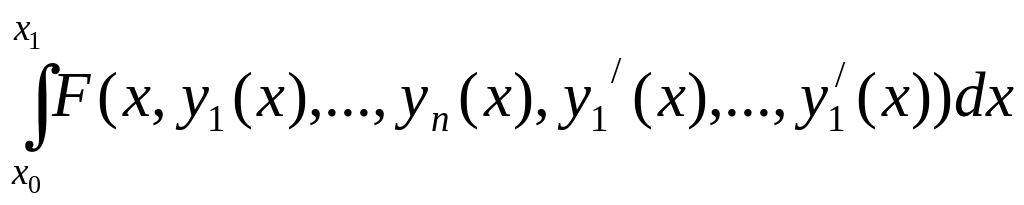
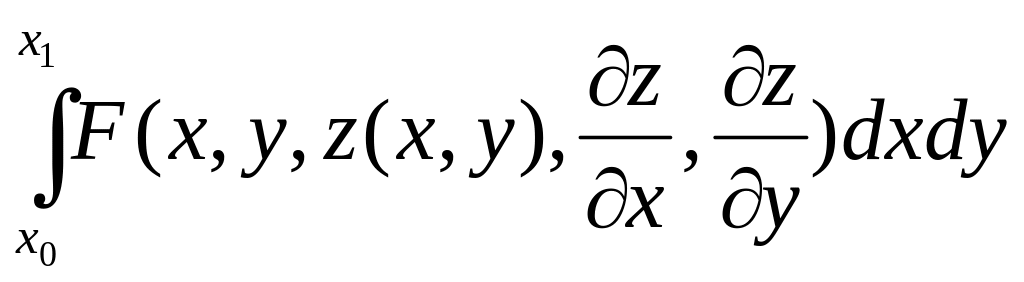