32. Второй метод Лагранжа.
Рассматривается
система
(1)
Теорема 1:
Если
существует дифференцируемая функция
,
называемая функцией Ляпунова,
удовлетворяющая в окрестности начала
координат следующим условиям:
1) 
,
причём
лишь при
,
.
2) 
,
при
,
то точка покоя
системы (1) устойчива.
Производная
в условии 2) взята вдоль интегральных
кривых системы (1).
Доказательство:
Поверхности уровня в окрестности точки покоя, которая является точкой строгого минимума, являются замкнутыми и окружают точку покоя.
Рассмотрим
поверхность уровня
, которая целиком лежит в
окрестности,
т.е.
,
но не проходит через начало координат.
Выберем
окрестность
так, чтобы
окрестность
целиком лежала внутри поверхности
.
Если начальная точка с координатами
,
находилась в
окрестности,
то
,
то при
точка траектории, которая проходит
через точку
не выйдет за пределы
окрестности
начала координат в силу условия 2)
теоремы.
Теорема 2: (т. Ляпунова для ассимптотичной устойчивости)
Если существует дифференцируемая функция Ляпунова , удовлетворяющая следующим условиям:
1) 
имеет строгий минимум в начале координат
.
2) производная
функция
,
вычисляемая вдоль интегральных кривых
системы (1):
,
причём вне сколь угодно малой окрестности
начала координат, т.е. при
,
производная
,
где
постоянная, то точка покоя
,
системы (1) асимптотически устойчива.
Доказательство:
Условия
теоремы выполнены, то если
можно выбрать
,
что траектория, начальная точка которой
не выйдет из
окрестности
начала координат.
Вдоль
траектории функция
монотонно убывает с возрастанием
.
Следовательно, существует 
Надо
показать, что
.
Откуда будет следовать, что
,
.
Первое условие теоремы только в начале координат.
Допустим,
что
.
Тогда
возьмём за
окрестность,
но здесь
,
проинтегрируем это неравенство от
до
:
или
При
достаточно большом
правая часть отрицательна и , следовательно,
,
что противоречит условию 1).
Пример 1:
,
1) 
,
2) 
Решение , асимптотически устойчиво.
Пример 2:
,
1) ,
2) 
Решение , асимптотически устойчиво.
Исследование проблемы устойчивости по первому приближению.
При
исследовании на устойчивость точки
покоя
,
системы
(1), где
дифференцируемая окрестности начала
координат функция.
Применяется следующий метод:
Систему (1) представляют в окрестности начала координат:
,
(2)
Система
,
(3)
Называется системой первого приближения для системы (1).
Теорема 3:
Если
система (2) стационарна в первом
приближении, все числа
,
в достаточно малой окрестности начала
координат при
удовлетворяют неравенствам:
,
где
и
постоянные.
и
все корни характеристического уравнения:
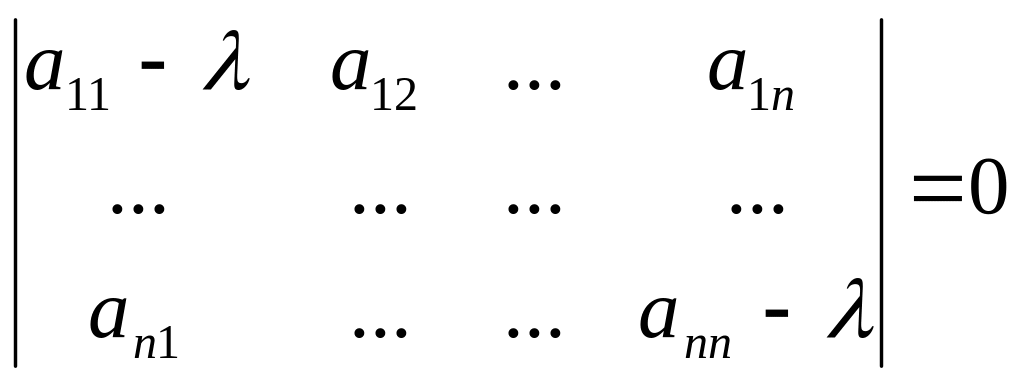(4)
имеют отрицательные действительные части, то тривиальное решение , системы (1) асимптотически устойчиво.
Теорема 4:
Если система (2) стационарна в первом приближении, все функции , удовлетворяют условиям предыдущей теоремы, и хотя бы один корень характеристического уравнения (4) имеет положительную действительную часть, то точка покоя , системы (2) неустойчива.
В критическом случае, когда действительная часть и хотя бы одного корня равна нулю, на устойчивость начинают влиять нелинейные члены и исследование на устойчивость по первому приближению невозможно.
Пример 1:
Нелинейные члены удовлетворяют условиям теорем 3. и 4. Исследуем на устойчивость точку покоя , .
,
, 
Решение , неустойчиво.
Пример 2:
Разлагая
по формулам Тейлора, получим:
, 
,
где
удовлетворяют
теоремам 4. и 5.
, 
Решение , асимптотически устойчиво.