Обыкновенные дифференциальные уравнения.

Глава 1. Линейные дифференциальные уравнения n-го порядка.

ЛЕКЦИИ 1-2.

1. Введение.

Линейные уравнения – это наиболее разработанная часть теории диф. уравнений, так как они либо описывают реальные процессы, либо дают первое приближение и во многих случаях по этому приближению можно судить о характере изучаемого явления.

Линейным дифференциальным уравнением называется уравнение вида

, (1)

где р_i(х), f(x) определены и непрерывны в интервале (а,b).

Тогда уравнение (1) имеет единственное решение у = у(х), удовлетворяющее начальным условиям:

при х = х₀, где а - любые заданные числа. Это решение определено и n раз дифференцируемо для .

Особых решений уравнение (1) не имеет. Если f(x)≡0, то уравнение (1) называется однородным:

, (2).

Для сокращения записи введём линейный дифференциальный оператор:

, (3).

Тогда уравнение (1)можно записать в виде:

L[y] = f(x) (1), а однородное уравнение L[y] = 0 (2).

Запишем очевидные свойства оператора L:

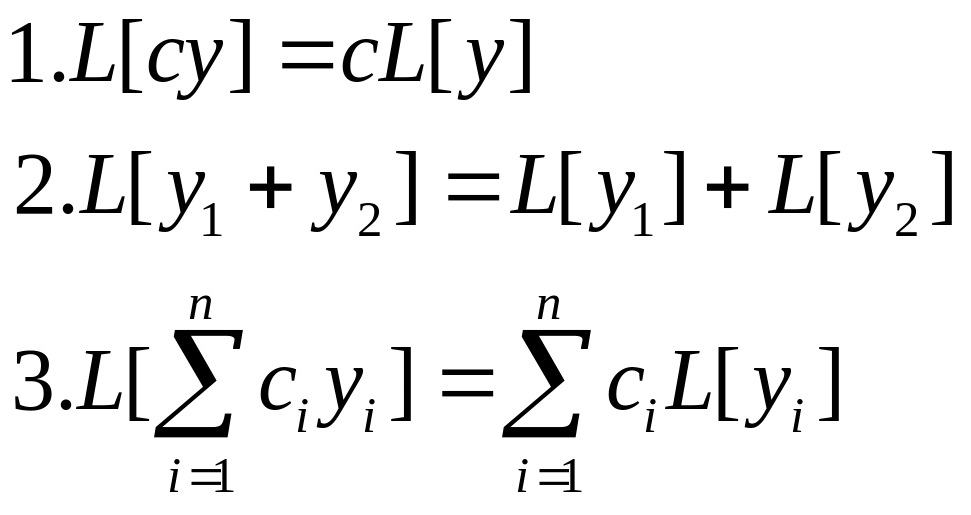
Определение. Функцию Z(x) = U(x) + iV(x) будем называть комплексной функцией от вещественной переменной х. U(x) u V(x) называются соответственно действительной и мнимой частями комплексной функции Z(x).

Теорема. Если комплексная функция у(х) является решением однородного уравнения (2), то её вещественная и мнимая части являются вещественными решениями этого уравнения.

Доказательство. y(x)=y₁(x)+i y₂(x) является решением уравнения (2).

. Тогда .

Пример.

2. Понятие о линейной независимости функций.

Определение. Функции y₁, y₂,…, y_n называются линейно независимыми в интервале (a,b), если между ними не существует соотношения вида: (1), где - постоянные числа, не равные нулю одновременно. В противном случае функции называются линейно зависимыми.

Очевидно, что если одна из функций тождественно равна нулю в интервале (a,b), то эти функции линейно зависимы в (a,b).

Пример 1. Функции (2) линейно независимы в интервале . Соотношение в котором не все равны нулю, не может выполняться тождественно, так как уравнение n-1 степени не может иметь более чем n-1 корней.

Пример 2. Пусть - различные числа. Тогда функции

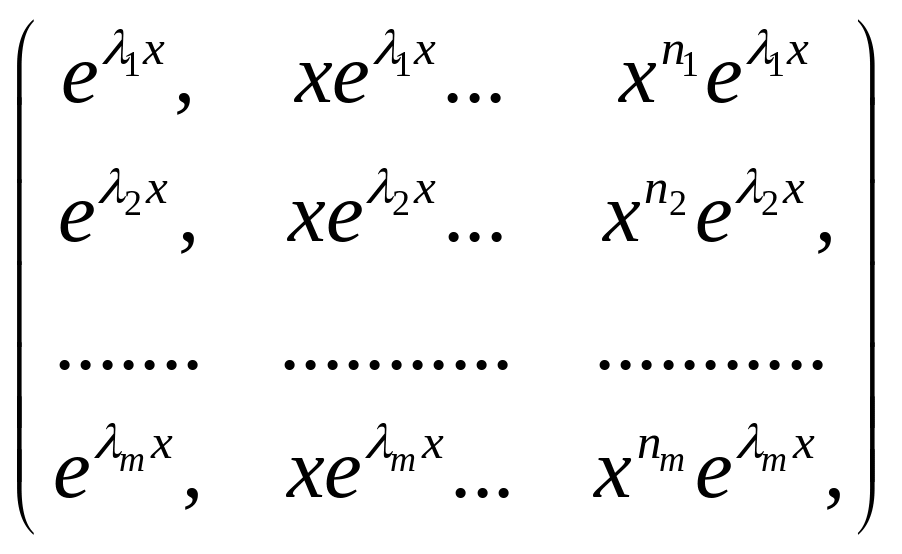(3), где n₁, n₂,…, n_m – целые неотрицательные числа, линейно независимы в интервале .

Пример 3. Пусть - различные числа. Тогда функции

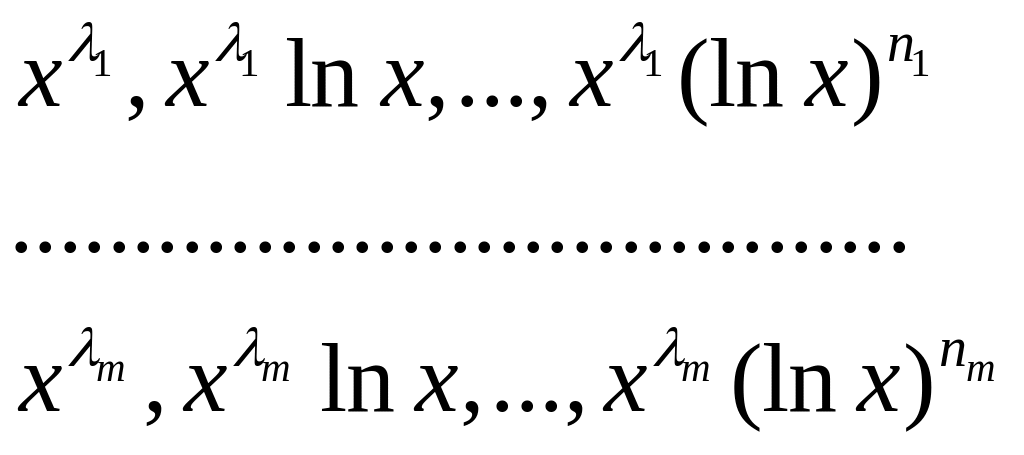(4), где n₁, n₂,…, n_m – целые неотрицательные числа, линейно

независимы в интервале .

Пример 4. Функции линейно зависимы в интервале , так как при всех х справедливо соотношение .

Пример 5. Функции линейно зависимы в интервале , так как справедливо при всех х.

3. Необходимое условие линейной зависимости n функций.

Пусть функции , имеют производные предела (n-1).

Рассмотрим определитель: 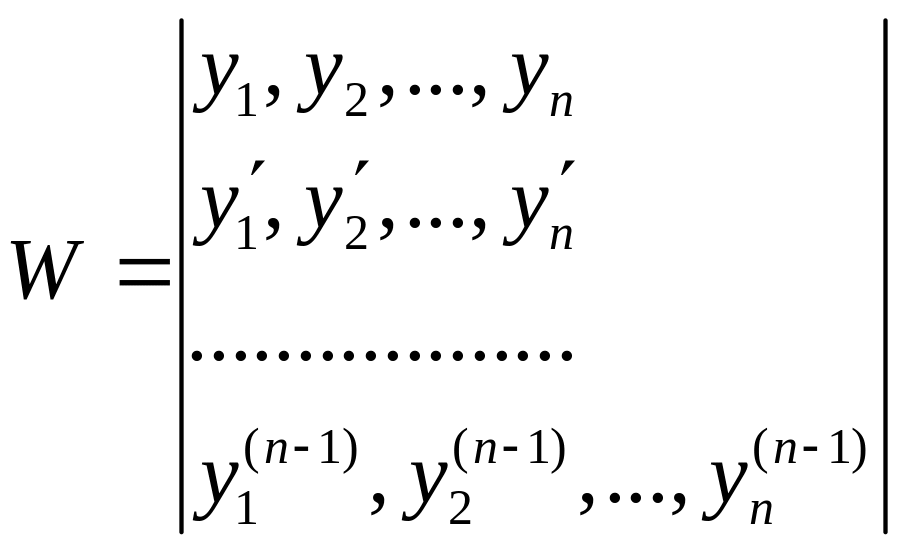(1)

W(x) называется определителем Вронского для функций .

Теорема 1. Если функции линейно зависимы в интервале (a,b), то их вронскиан W(x) тождественно равен нулю в этом интервале.

Доказательство. По условию теоремы выполняется соотношение

, (2) где не все равны нулю. Пусть . Тогда

(3). Дифференцируем это тождество n-1 раз и,

подставляя вместо их полученные значения в определитель Вронского,

получаем:

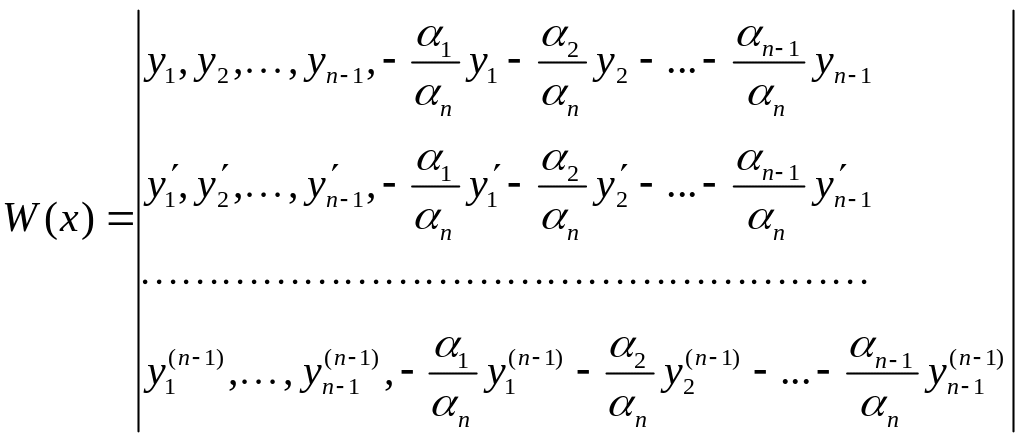(4).

В определителе Вронского последний столбец является линейной комбинацией предыдущих n-1 столбцов и поэтому равен нулю во всех точках интервала (a,b).

Теорема 2. Если функции y₁,..., y_n являются линейно независимыми решениями уравнения L[y] = 0, все коэффициенты которого непрерывны в интервале (a,b), то вронскиан этих решений отличен от нуля в каждой точке интервала (a,b).

Доказательство. Допустим противное. Существует Х₀, где W(Х₀)=0. Составим систему n уравнений

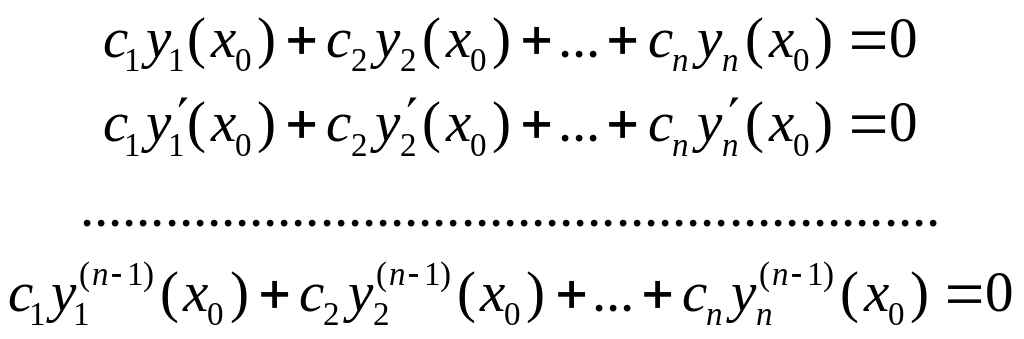(5).

Очевидно, что система (5) имеет ненулевое решение. Пусть (6).

Составим линейную комбинацию решений y₁,..., y_n.

(7).

У(х) является решением уравнения L[y] = 0. Кроме этого . В силу теоремы единственности решения уравнения L[y] = 0 с нулевыми начальными условиями может быть только нулевым, т.е. .

Мы получаем тождество , где не все равны нулю, а это означает, что y₁,..., y_n линейно зависимы, что противоречит условию теоремы. Следовательно, нет такой точки где W(Х₀)=0.

На основе теоремы 1 и теоремы 2 можно сформулировать следующее утверждение. Для того, чтобы n решений уравнения L[y] = 0 были линейно независимы в интервале (a,b), необходимо и достаточно, чтобы их вронскиан не обращался в нуль ни в одной точке этого интервала.

Из доказанных теорем также следуют такие очевидные свойства вронскиана.

1. Если вронскиан n решений уравнения L[y] = 0 равен нулю в одной точке х = х₀ из интервала (a,b), в котором все коэффициенты р_i(x) непрерывны, то он равен нулю во всех точках этого интервала.

2. Если вронскиан n решений уравнения L[y] = 0 отличен от нуля в одной точке х = х₀ из интервала (a,b), то он отличен от нуля во всех точках этого интервала.

Таким образом, для линейности n независимых решений уравнения L[y] = 0 в интервале (a,b), в котором коэффициенты уравнения р_i(x) непрерывны, необходимо и достаточно, чтобы их вронскиан был отличен от нуля хоть в одной точке этого интервала.