8.3.2. Модель бп

Для цієї моделі характерні умови:

; , а ,

тобто дефект і приймальний перетворювач містяться в трубці випромінювання перетворювача (рис. 8.18).

Відповідно до розглядуваних умов акустичний тиск прийнятого сигналу для бездефектного «чистому» тракту становить

.

Акустичний тиск в області дефекту відповідно до формули (8.6)

.

Тепер можна визначити тиск в області приймача, який створювався б вторинним випромінювачем, розміщеним замість дефекту

.

Тиск у приймачі за наявності непрозорого дефекту

. (8.21)

У загальному випадку з урахуванням прозорості дефекту вираз (8.21) матиме вигляд

.

Як було зазначено в п. п. 8.2.1 , тому

,

де

– коефіцієнт тіні, який містить всю амплітудну інформацію про дефект (сукупна інформація про розмір і прозорість дефекту).

8.3.3. Модель вп

Для цієї моделі характерні умови: , і .

Усі ультразвукові процеси випромінювання-приймання відбуваються у ближніх зонах, тобто у своїх трубках випромінювання. Для розрахунку коефіцієнта акустичного тракту використаємо енергетичний підхід, використовуваний в п.8.2.6. У цьому разі енергетичний підхід доречний, оскільки розрахунок на базі характеристик напрямленості випромінювання досить ускладнений і не наочний, а точність результатів є умовною у зв'язку з безліччю обмежень і усереднень.

Згідно з енергетичним підходом і попередніми умовами випромінювана в трубку випромінювання ультразвукова потужність

. (8.22)

Вважаючи, що ультразвукова хвиля плоска і перетинає межу поділу двічі, потужність прийнятого сигналу при «чистому» тракті визначаємо за формулою

.

Тепер можна вичислити потужність акустичної енергії в приймачі, яку передав би в приймач вторинний випромінювач в розмірі

.

Ця енергія (потужність) вилучається з . Дефект може бути частково прозорим, тобто мати ненульову прозорість , тоді в приймачі за рахунок прозорості дефекту додасться потужність

.

У результаті отримаємо

.

З виразу (8.22) визначаємо коефіцієнт акустичного тракту

, (8.23)

або, якщо розкласти вираз під коренем в біном Ньютона, то

де

– коефіцієнт тіні, який містить усю амплітудну інформацію про дефект (сукупну інформацію про розмір і прозорість дефекту).

8.3.4. Модель гп

Це модель акустичного тракту методу проходження в імерсійному середовищі. Складність розрахунку цього акустичного тракту порівняно з попередніми полягає в побудові його еквівалентної схеми (або схеми заміщення). Тут ОК з дефектом, що міститься в ньому, розміщений в іншому середовищі. Типовим представником такого тракту є тракт тіньового методу контролю в імерсійному середовищі (рис. 8.19).

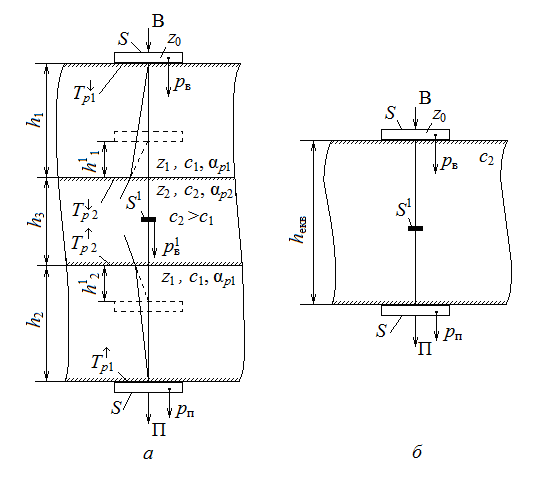
Рис. 8.19. Акустичний тракт імерсійного методу проходження (а)

і його еквівалентна схема (б)

Застосуємо випробуваний раніше спосіб перетворення складної схеми тракту в просту, зручну для розрахунку (див. п.8.2.2). Відповідно до рис. 8.19, а можна обчислити еквівалентні параметри тракту

; .

Утворилася нова схема акустичного тракту (рис. 8.19, б) з параметрами

, і .

Тепер залишається тільки з'ясувати, до якої розрахункової моделі належить одержано еквівалентна схема акустичного тракту.

1. Якщо всі процеси випромінювання і приймання відбуваються в дальніх зонах, тобто коли і , тоді

.

.

2. Якщо всі процеси випромінювання і приймання відбуваються у різних зонах, тобто коли і , тоді

.

3. Якщо ж усі процеси випромінювання і приймання відбуваються у ближніх зонах, тобто коли і , тоді

.