7.2.5. Еквівалентна схема п′єзоелемента
Резонансна і антирезонансна частоти. Оборотність п’єзоелектричних перетворювачів дозволяє подати п’єзоелемент у вигляді двополюсника, що об'єднує системи електричного збудження механічних коливань і зняття електричного сигналу, пропорційного їх амплітуді.
Як і всяке тверде пружне тіло п’єзоелемент має власну частоту механічних коливань. Спектр власних частот визначається розмірами і конструктивним формами п’єзоелемента, способом кріплення, пружними властивостями п'зоматеріалу і типом деформацій в процесі коливань (типом п′єзоефекту, наприклад, подовжнім, поперечним або зсувним).
Для того щоб заданий тип коливань міг бути збуджений, необхідно, щоб електричне поле, створюване підведенням електричного сигналу, спричинило на основі зворотного п’єзоефекту відповідний тип деформацій в тілі п’єзоелемента.
Увімкнемо
п’єзоелемент, в якому збуджуються
товщинні коливання, як двополюсник в
електричне коло зі змінною напругою
(рис.7.20, а).
Амплітудно-частотна характеристика
(АЧХ) в області механічного резонансу
має явно виражені нуль і полюс (рис.7.20,
б),
між якими реактивна провідність має
індуктивний характер. У решті частини
спектра (за межами резонансного проміжку
)
провідність має ємнісний характер.
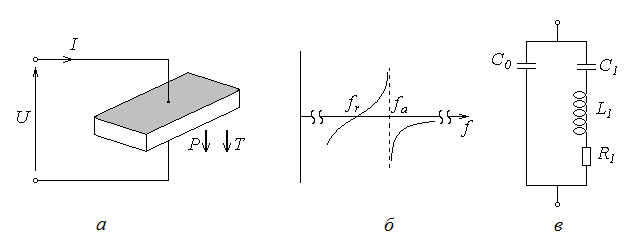
Рис.7.20. Побудова еквівалентної схеми п’єзоелемента: п’єзоелемент (а) як двополюсник і його частотна характеристика (б), еквівалентна схема ненавантаженого п’єзоелемента (в)
Такому стану АЧХ
двополюсника відповідає електрична
схема (рис.7.20, в).
Очевидно, що для цієї схеми частота
послідовного резонансу
визначається виразом
,
а частота паралельного резонансу (антирезонансу)
.
Розглянемо тепер
співвідношення між коефіцієнтом
електромеханічного зв'язку
,
величиною п’єзоелемента (його геометричною
ємністю
)
і частотами резонансного проміжку (
і
).
Співвідношення
ємностей
і
еквівалентної схеми залежить від
величини коефіцієнта електромеханічного
зв'язку і рівне
.
Тоді
,
звідки
.
Для малих значень коефіцієнта зв'язку
.
Таким чином,
визначивши резонансний проміжок
,
можна обчислити коефіцієнт електромеханічного
зв'язку
.
Тепер розглянемо, як формується амплітудне значення деформації товщини п′єзоелемента на парних і непарних гармоніках (рис.7.21).
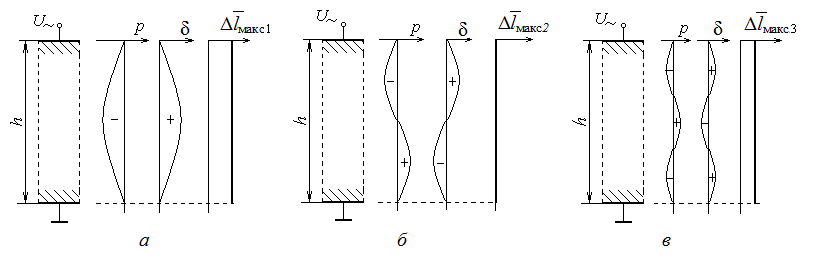
Рис.7.21. Утворення товщинних деформацій в п’єзоелементі на вищих
гармоніках при безперервному збудженні
На непарних
гармоніках
уздовж товщини зразка укладається
непарна кількість півхвиль, наприклад,
акустичного тиску (рис.21, а,
в).
У результаті виникає інтегральна
деформація
.
Таким чином, на непарних гармоніках
може настати резонанс.
На парних гармоніках
інтегральна деформація дорівнює нулю
.
Резонанс на парних гармоніках не виникає.
Ці міркування стосуються випадку безперервного збудження. Під час імпульсного (ударного) збудження не виключено виникнення коливань і на парних гармоніках.
Приєднана до п’єзоелемента маса знижує його резонансну частоту.
Добротність
перетворювача. Значущим
параметром п′єзоперетворювача є
добротність
як оцінювання його резонансних
властивостей монокристалічних
перетворювачів (наприклад кварцу)
.
Добротність керамічних перетворювачів
можна змінювати в широких межах через
зміну хімічного складу або введенням
наповнювачів. Зазвичай промислові марки
п’єзокераміки мають добротність в
межах 15…1000.
За частоти збудження нижчої за резонансну амплітуда зсуву дорівнює статичній зміні товщини
.
За резонансу амплітуда зсуву підвищується і визначається добротністю
.
Добротність
пов'язана з коефіцієнтом
загасання (див. разд.4)
де
логарифмічний декремент загасання в
п′єзоматеріалі.
Динамічний опір
,
який визначає механічні втрати, можна
визначити з добротності коливальної
системи
.
Оскільки
,
а
,
то
.
Чим гірша добротність коливальної системи, тим нижча її резонансна частота (з теорії лінійних електричних кіл).