Пар. Испарение. Объяснение испарения. Температура испаряющейся жидкости. Скорость испарения. Конденсация. Точка росы. Скорость конденсации. Насыщенный пар. Свойства насыщенного пара.
Пар – одно из агрегатных состояний вещества (газообразное)
Испарение – процесс перехода вещества из жидкого состояния в газообразное.
Испаре́ние — это процесс, при котором с поверхности жидкости или твёрдого тела вылетают (отрываются) частицы (молекулы, атомы), при этом Ek > Eп.
Температура испаряющейся жидкости:
Если жидкость изолирована от окружающих тел
Жидкость не изолирована
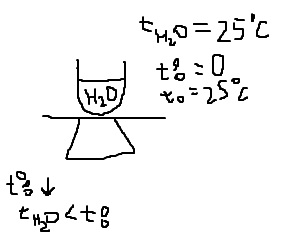
Скорость испарения зависит:
А) от рода вещества
Б) от температуры
В) От площади поверхности
Vисп = Nвылет : t
Vисп = 1:сек
Конденсация – переход молекул из парообразного состояния в жидкость.
Виды конденсации:
А) на более холодных предметах (центрах конденсации)
Б) идущая параллельно испарению
Точкой росы при данном давлении называется температура, до которой должен охладиться воздух, чтобы содержащийся в нём водяной пар достиг состояния насыщения и начал конденсироваться в росу
. Точка росы определяется относительной влажностью воздуха. Чем выше относительная влажность, тем точка росы выше и ближе к фактической температуре воздуха. Чем ниже относительная влажность, тем точка росы ниже фактической температуры. Если относительная влажность составляет 100 %, то точка росы совпадает с фактической температурой.
Формула для приблизительного расчёта точки росы в градусах Цельсия:
где
Tp = точка росы,
a = 17.27,
b = 237,7 °C,
,
T = температура в градусах Цельсия,
RH = относительная влажность в объёмных долях (0 < RH < 1.0),
ln — натуральный логарифм.
Формула обладает погрешностью ±0.4 °C в следующем диапазоне значений:
0 °C < T < 60 °C
0.01 < RH < 1.0
0 °C < Tр < 50 °C
Скорость конденсации:
Vк = Nвлет : t
Vк = 1: сек
Vк = m : t
Зависит от:
А) температуры
Б) площади поверхности
Насыщенный пар – это пар, который находится в динамическом равновесии со своей жидкостью
При данной температура давление и плотность максимальны
При повышении температуры давление и плотность увеличиваются, но не по линейному закону.
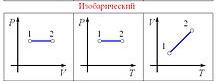
Изобарный процесс. Метод реализации процессов. Уравнение изобарного процесса. Закон Гей-Люсака. Изобара в координатах pV;pT;VT.
Изобарный процесс -это процесс, происходящий в физической системе при постоянном давлении (p = const). При этом изменяются объем и температура, следовательно, совершается работа dA = pdV и изменяется внутренняя энергия dU.
Для осуществления изобарного процесса к системе надо подводить или отводить теплоту, которая расходуется на работу расширения и изменение внутренней энергии.
Изобарный процесс можно описать уравнением:
V = VoaT, где V – объем газа при абсолютной температуре Т; Vo — объем газа при температуре 0оС; a — температурный коэффициент объемного расширения газа, равный 1/273 К-1.
Закон теплового расширения газов
Это один из основных газовых законов, описывает изобарные процессы в идеальных газах. Закон открыт независимо Ж. Л. Гей-Люссаком в 1802 г. и Дж. Дальтоном в 1801 г.
Согласно закону теплового расширения газов: объем V данной массы газа при постоянном давлении газа прямо пропорционален изменению температуры:
V = Vo(1+t),
Vo — начальный объем газа;
t — разность начальной и конечной температур;
- коэффициент теплового расширения газов, = (1/273,15)К-1.
Коэффициент одинаков для всех газов.
В термодинамической шкале температур закон Гей-Люссака можно записать следующим образом:
При постоянном давлении для постоянной массы газа (p = const, m = const):
V1/V2 = T1/T2 = const.
Закон справедлив только для идеальных газов, реальные газы подчиняются ему при температурах и давлениях, далеких от критических значений. Является частным случаем уравнения Клайперона.
