4. Расчет скорости псевдоожижения.

Критерий Архимеда рассчитывается по формуле

Где Аr – критерий Архимеда;

d_экв – эквивалентный диаметр, м;

ρ_ч – кажущаяся плотность частиц, кг/м³ ;

ρ – плотность среды, кг/м³;

g =9,81 – ускорение свободного падения, м/с²;

μ – вязкость среды, Па*с.

Рассчитаем значение числа Архимеда для различных значений эквивалентного диаметра:

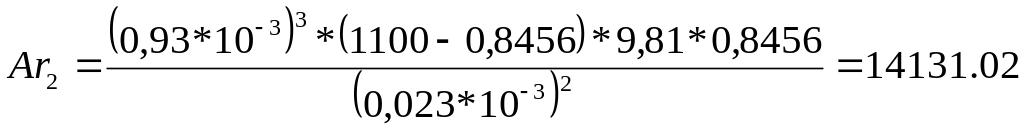
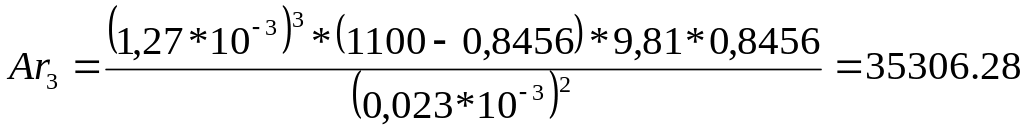
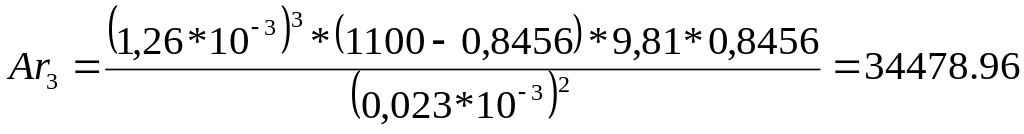
По данным значениям числа Архимеда находим первое критическое значение числа Рейнольдса по:

Где Re_кр1 – первое критическое значение числа Рейнольдса;

Ar – число Архимеда.

Рассчитаем первое критическое значение числа Рейнольдса:

По рассчитанному значению числа Рейнольдса рассчитывают значение первой критической скорости – начало псевдоожижения:

Где w_кр1 – первая критическая скорость, м/с;

μ – вязкость среды, Па*с;

Re_кр1 – первое критическое значение числа Рейнольдса;

d_экв – эквивалентный диаметр, м;

ρ – плотность среды, кг/м³.

Рассчитаем значения первой критической скорости для всех значений эквивалентного диаметра:

м/с

м/с

м/с

м/с

5. Расчет второй критической скорости.

Вторая критическая скорость (конец псевдоожижения) рассчитывается аналогично, в выражении для числа Архимеда и критической скорости вместо эквивалентного диаметра берётся минимальный. Т.к. для всех четырёх вариантов значение минимального диаметра одинаково (d_min = 0.25 мм), то и значения чисел Архимеда и Рейнольдса, а также вторая критическая скорость для всех случаев будет одинакова. Число Рейнольдса рассчитывают по:

Где Re_кр2 – второе критическое значение числа Рейнольдса;

Ar – число Архимеда для минимального диаметра.

Число Архимеда для минимального диаметра равно:

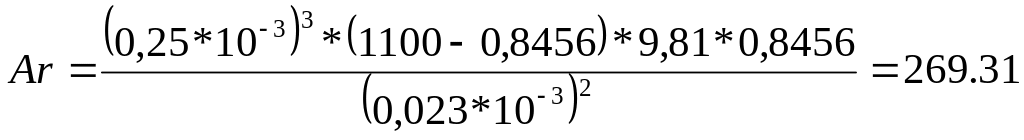
Число Рейнольдса равно

Вторая критическая скорость равна

м/с.

Найдем наибольшее значение числа псевдоожижения K_W по

Где K_wmax – максимальное число псевдоожижения;

W_кр2 – вторая критическая скорость, м/с;

W_кр1max – максимальная из четырёх значений первой критической скорости, м/с.

Максимальное значение числа псевдоожижения равно:

.

6. Расчет рабочей скорости псевдоожижения.

Т.к. число псевдоожижения не может быть больше 3,41, а в задании указано 5,2, то принимаем K_w = 3,3 для всех расчетов. Находим рабочие скорости по

Где w_раб – рабочая скорость, м/с;

K_w – число псевдоожижения;

W_кр1 – первая критическая скорость, м/с.

м/с

м/с

м/с

м/с

7. Определение диаметра аппарата.

Диаметр аппарата рассчитывают по:

Где D – диаметр аппарата, м;

S – площадь сечения аппарата, м².

Площадь сечения аппарата находят по:

S = Vc/Wраб

Где S – площадь сечения аппарата, м²;

V_c – секундный расход, м³;

W_раб – рабочая скорость, м/с.

Найдем секундный расход воздуха:

V_c – 5000/3600=1,389 м³/с;

Найдем площадь сечения аппарата для всех четырёх случаев:

S₁ = 1.389/ 0.7052 = 1.9697 м²;

S₂ = 1.389/ 0.6861=2.0245м²;

S₃ = 1.389/1.06664 =0.З022 м²;

S₄ = 1.389/ 1.05391=1.3179 м².

Sср=(1.9697+2.0245+1.3022+1.3179)/4=1.65358 м²

Диаметр аппарата для четырёх случаев равен:

Для всех случаев принимаем аппарат с диаметром 1800 мм.