Модуль №2

“Методи чисельного інтегрування і розв’язку диференціальних рівнянь”

Лекція №9 Чисельне диференціювання та інтегрування функцій.

Чисельне диференціювання. Наближення похідної формулами лівої, правої та центральної різниць другого-четвертого порядків. Аналіз похибок. Диференціювання поліномами Лагранжа і Ньютона.

Формули чисельного диференціювання важливі при обчисленні граничних значень у задачах із звичайними диференціальними рівняннями і диференціальними рівняннями в частинних похідних.

Основним принципом обчислення похідних є диференціювання інтерполяційного полінома. Для обчислення похідної першого порядку можна використовувати формули лівої, правої або центральної різниці.

(9.1)

де h – шаг або прирощення аргументу; f(x) – значення функції в точці x.

Розглянемо чисельний процес наближення похідної

де h_k – прирощення аргументу, параметр, якому будемо надавати значення 0.1; 0.01; 0.001; 10^-4, … , k = 1 …n...

Якщо функцію f(x) у точці x₀ = 0 обчислювати з точністю до 10 знаків, то точність обчислення похідної спочатку збільшується при зміні h_k до 1е-5 , а потім зменшується.

Формули центральної різниці

Якщо функцію f(x) можна обчислювати праворуч і ліворуч від x, то найкраща двоточкова формула I-го порядку для f’(x) має вигляд

, (9.2)

де - похибки усікання, що мають другий порядок малості.

Центрована формула O(h⁴).

Припустимо, що і що x - 2h, x – h, x + h, x + 2h [a, b], тоді

, (9.3)

де , c = c(x) [a, b].

Аналіз похибок і вибір оптимального кроку

При обчисленні на ПЕВМ існують похибки округлення E_окр(f, h), такі, що

f(x₀ – h) = y_-1 + e_-1 f(x₀ + h) = y₁ + e₁.

У формулі для центральної різниці

загальний залишковий член E(f, h) має частину обумовлену похибкою округлення і частину обумовлену похибкою усікання

. (9.4)

Оптимальна величина кроку h, при якому мінімальна загальна похибка дорівнює

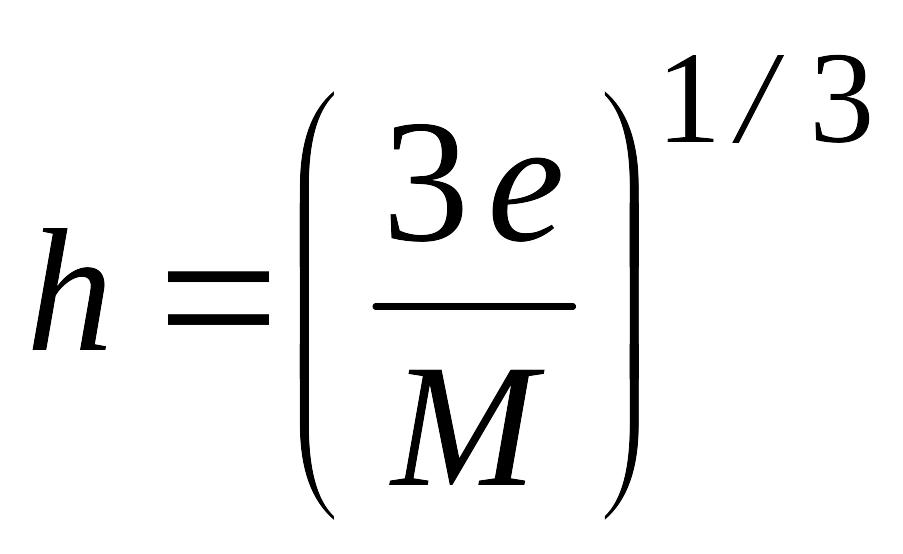, (9.5)

де ;

Графіки залежності похибки від величини кроку h для функції cos(x) для цих формул мають вигляд

1. Г

   h_опт=0,00114

   O(h²)

   4₁₀^-6 -

   

   2₁₀^-6

   

   4₁₀^-7

   

   2₁₀^-7

   

   h

   раниця похибок Границя похибок

O(h⁴)

h_опт= 0,0223

h

0.001 0,002 0,004 0,02 0,04 0,06

Формули центральної різниці для похідних вищого порядку

Щоб одержати формули центральної різниці для похідних вищих порядків, можна скористатися розкладанням функцій та в ряд Тейлора.

Підсумовуючи і виділяючи далі з отриманого виразу відповідні похідні, одержимо:

для

,

, (9.7)

;

для формул центральної різниці порядку :

,

, (9.8)

.

Оптимальне значення кроку для порядку задається формулою

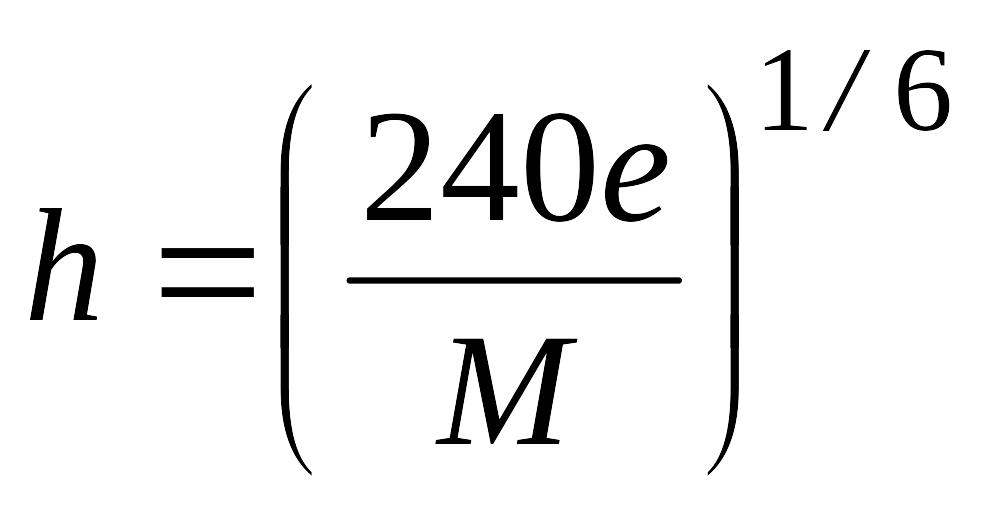, де .

Взагалі, при виконанні чисельного диференціювання точність обчислень складає тільки половину точності, яку допускає комп'ютер.

Диференціювання поліномами Лагранжа і Ньютона

Якщо чисельне значення похідної одержано за спостереженнями у вигляді табличної функції, то можна скористатися методами побудови кривої за точками із застосуванням техніки найменших квадратів і формул диференціювання отриманих функцій.

Для чисельного диференціювання використовують при цьому інтерполяційні формули Лагранжа і Ньютона. Кінцеві формули для центральних різниць співпадають з формулами, які отримані при розкладанні функції в ряд Тейлора [див. 5.7, 5.8]. Деякі кінцеві формули для правої і лівої різниці порядку отримані диференціюванням інтерполяційного полінома Лагранжа або Ньютона мають вигляд:

- права різниця;

- ліва різниця;

- права різниця; (9.9)

- ліва різниця.

- права різниця;

- права різниця;

У всіх формулах сума коефіцієнтів з урахуванням знаків дорівнює нулю.

Лекція №10 Чисельне інтегрування.

Квадратурні формули трапецій, Симпсона і Буля. Складені формули трапецій, Симпсона і Буля. Рекурентні і адаптивні процедури чисельного інтегрування. Інтегрування по Гаусу-Лагранжу з оптимальним вибором вузлів інтегрування.

Чисельне інтегрування є основним методом, який використовується інженером для обчислення означених інтегралів, які неможливо обчислити аналітично.

Введення в квадратуру

Завдання полягає в тім, щоб знайти наближення означеного інтеграла від на інтервалі [a; b], обчислюючи функцію в кінцевому числі обраних точок.

Припустимо, що

формула виду

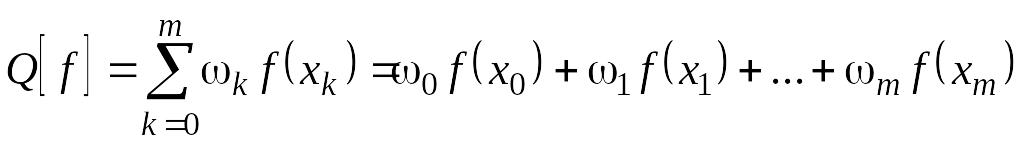, (10.10)

що має властивість

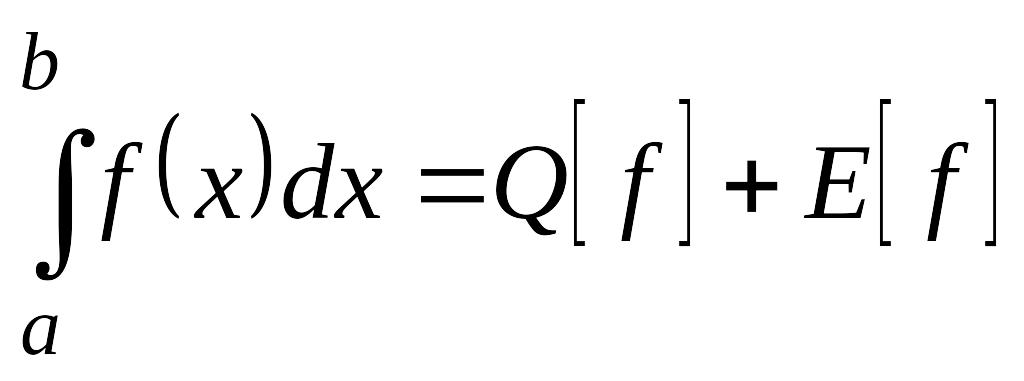(10.11)

називається формулою чисельного інтегрування або формулою квадратури. Член - називається похибкою усікання для інтегрування. Значення називаються вузлами квадратури, а - вагами. У залежності від застосування вузли вибираються різними способами. Для формул трапецій, Симпсона і Буля вибираються рівностоячі вузли. Для квадратури Гауса-Лежандра обрані вузли повинні бути нулями поліномів Лежандра.