Методи мінімізації функції багатьох змінних

Методи які відносяться до задач безумовної оптимізації багатьох змінних можна поділити на три класи:

1. методи нульового порядку (прямі методи), які базуються на обчисленні тільки цільової функції;

2. методи першого порядку, в яких використовується значення частинних похідних першого порядку;

3. методи другого порядку, які використовують значення частинних похідних другого порядку.

Прямі методи

Прямі методи або методи нульового порядку не вимагають знання цільової функції в явному вигляді. Вони не вимагають регулярності і безперервності цільової функції й існування похідних. Це є істотною перевагою при вирішенні складних технічних і економічних задач. При реалізації прямих методів істотно скорочується етап підготовки рішення задачі, тому що немає необхідності у визначенні перших і других похідних. Прямі методи в основному носять евристичний характер. До прямих методів відноситься цілий ряд алгоритмів, що відрізняються по своїй ефективності: метод Гауса, метод Хука і Дживса і його модифікація – метод Розенброка, метод Нелдера-Міда, метод сполучених напрямків Пауэлла, методи випадкового пошуку. Методи призначені для рішення безумовних задач оптимізації

.

Алгоритм Хука і Дживса

Метод Хука — Дживса (англ. Hooke — Jeeves), также как и алгоритм Нелдера-Мида, служит для поиска безусловного локального экстремума функции и относится к прямым методам, то есть опирается непосредственно на значения функции. Алгоритм делится на две фазы: исследующий поиск и поиск по образцу.

На начальном этапе задается стартовая точка (обозначим её 1) и шаги h_i по координатам. Затем замораживаем значения всех координат кроме 1-й, вычисляем значения функции в точках x₀+h₀ и x₀-h₀ (где x₀ — первая координата точки, а h₀ — соответственно значение шага по этой координате) и переходим в точку с наименьшим значением функции. В этой точке замораживаем значения всех координат кроме 2-й, вычисляем значения функции в точках x₁+h₁ и x₁-h₁, переходим в точку с наименьшим значением функции и т. д. для всех координат. В случае, если для какой-нибудь координаты значение в исходной точке меньше, чем значения для обоих направлений шага, то шаг по этой координате уменьшается. Когда шаги по всем координатам h_i станут меньше соответствующих значений e_i, алгоритм завершается и точка 1 признаётся точкой минимума.

Иллюстрация первого этапа для двух координат:

Таким образом, проведя исследующий поиск по всем координатам, мы получим новую точку, с наименьшим значением функции в окрестности (обозначим ее 2). Теперь можно осуществлять переход ко 2 фазе алгоритма.

На этапе поиска по образцу откладывается точка 3 в направлении от 1 к 2 на том же расстоянии. Её координаты получаются по формуле  , где x_i — точка с номером i, λ — параметр алгоритма, обычно выбирающийся равным 2. Затем в новой точке 3 проводится исследующий поиск, как на 1 фазе алгоритма, за исключением того, что шаг на этой фазе не уменьшается. Если на этой фазе, в результате исследующего поиска, удалось получить точку 4, отличную от точки 3, то точку 2 переобозначим на 1, а 4 на 2 и повторим поиск по образцу. В случае если не удаётся найти точку 4, отличную от точки 3, то точку 2 переобозначим на точку 1 и повторим 1-ю фазу алгоритма — исследующий поиск.

Иллюстрация второго этапа для двух координат:

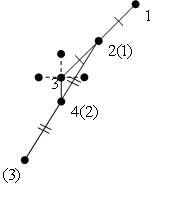
В скобках отмечены имена точек после переобозначения. На иллюстрации хорошо заметно, как алгоритм корректирует своё направление в зависимости от найденных значений функции.