Лекція №5 Екстремальні задачі. Методи мінімізації функцій однієї змінної.	23
Лекція №6 Числові методи мінімізація функцій багатьох змінних.	28
Лекція №7 Методи інтерполяції таблично заданих функцій.	32
Лекція №8 Методи апроксимації і наближення функцій.	36
Лекція №9 Чисельне диференціювання.	40
Лекція №10 Чисельне інтегрування.	43

Лекція №5 Екстремальні задачі. Методи мінімізації функцій однієї змінної

Цілі і задачі оптимізації. Методи знаходження мінімуму функцій однієї змінної. Методи дихотомії, золотого перетину, Фібоначі, квадратичної і кубічної інтерполяції.

Основні поняття

Оптимізація – це пошук найкращого (найбільш ефективного) рішення.

Критерій оптимізації – це показник, який дозволяє визначити якість отриманого розв’язку задачі.

Керовані змінні – це такі параметри задачі, значення яких можна змінювати, підвищуючи при цьому якість розв’язку задачі.

Цільова функція – це функція, що пов’язує керовані змінні та критерії оптимізації таким чином, що дозволяє обчислити значення критерію при довільних значеннях керованих змінних.

Ограничения – математические соотношения, отражающие условия, накладываемые на аргументы или значения целевой функции.

Наприклад, для задач апроксимації найбільш часто використовуваними цільовими функціями є функції засновані на квадратичному, мінімаксному або абсолютному критеріях: , , , де - відхилення значень функції обчислених в точках x_i від емпіричних.

Оптимізація при обмеженнях (лінійна)

Цільова функція

Q(X) =P₁ X₁ +Р₂Х₂ + . . . +Р_nХ_n → Признак оптимальности

Основные ограничения

a11x1 +a12Х2 +...+a1nXn < / > / = b1,

...

am1x1 +am2Х2 +...+amnXn < / > / = bm,

Дополнительные ограничения:

Условие целочисленности

Условие, что Х может принимать значения 0 и 1

Приклад: Задача о диете

цель - стоит задача минимизации стоимости набора продуктов

где c- стоимость единицы продукта; х - искомое количество продукта; n - количество продуктов в списке

Назначение - составить оптимальный набор продуктов

Условия решения - Имеется набор продуктов Х, необходимых для жизни человека. Каждый і-продукт при цене с_і имеет калорийность q_і и его количество в рационе не должно быть ниже х_імин. и не больше х_імакс –

Внеш. ограничения отсутсвуют

Внутр ограничения

-x_imin<=х_i<=х_імax.

Cуммарная калорийность не ниже заданной

Пример задача о диете из двух составляющих - жиров (сало) Х и углеводов (сахар)У. Человек должен потреблять:

- не менее 8 ед. жиров и 5 ед. углеводов.

- не более 18 ед. жиров и 31 ед. углеводов:

8<=X<=18

5<=Y<=31 (1)_

Калорийность жиров 11, углеводов 12

Суммарная калорийность не менее 220

Q =11X + 12Y >=220 (2)_

Цена жиров 2.5, углеводов 6

Z=2.5 X + 6Y (3)_

Найти Х и У

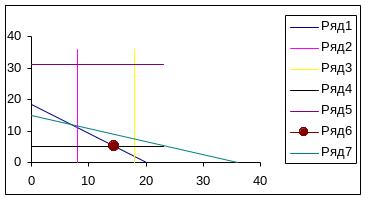
Вначале проводятся границы диапазонов изменения Х и У

Чтобы получить точки, удовлетворяющие условию (2), проведем прямую (например, положив сначала Х=0 - У=18,3, а затем У=0 - Х=20. Для того чтобы найти полуплоскость, удовлетворяющую неравенству 2, возьмем, например, произвольную точку, не лежащую на прямой, и проверим, удов­летворяет она условию или нет. Если удовлетворяет, то вся полуплоскость, в которой находится эта точка, является допустимой (по отношению к этому условию). В противном случае полуплоскость является недопустимой и за­штриховывается. Таким же образом поступим с условием 1 и снова исключим точки, не входящие в допустимую область. Графическое изображение этих неравенств воспроизведено на рис. 6.1. Все точки плоскости, не исключенные условиями, образуют допустимую область. Вследствие условий, налагаемых на знаки, она всегда лежит в первом квадранте плоскости.

Все точки, в которых целевая функция принимает значение 120, лежат на прямой 2,5 Х +6 У =120 — линии уровня Q == 120, принадлежащей числу 120. Все линии уровня, принадлежащие каким-либо другим значениям, также являются прямыми, причем параллельными прямой Q == 120. Если сместить прямую Q == 120 параллельно самой себе в одном направлении, то значения, принадлежащие линиям уровня, уменьшаются; при параллельном переносе в другом направлении они увеличиваются. В каж­дой точке допустимой области целевая функция принимает значение, принад­лежащее линии уровня, на которой лежит эта точка.

Направление, в котором следует осуществлять сдвиг, чтобы достичь меньших значений целевой функции, можно найти построением другой линии уровня, например Q=100. Путем параллельного переноса прямой в направле­нии меньшиx значений целевой функции в допустимой области достигают того, что параллельная прямая будет пересекать допустимую область только в одной точке. (В общем случае параллельная прямая может проходить по отрезку, лучу или прямой.) В примере точка Р, лежащая на линии уровня, принадлежащей числу 66 (см. рис. 6.2). Все другие допустимые точки лежат на линиях уровня, принадлежащих большим значениям. Все точки, лежащие на линиях уровня с меньшими значениями, являются недопустимыми. Таким об­разом, точка Р есть искомая оптимальная точка.

Заметим, что оптимальная точка является угловой точкой допустимой области. Точка Р не есть относительный минимум целевой функции, так как она вообще не имеет относительных экстремумов, т. е. Р не может быть найдена методом дифференциального исчисления.

Все задачи линейного программирова­ния с двумя переменными можно решить с помощью графического метода, объяснен­ного на этом примере.

Множество всех оптимальных решений задачи линейного программирования выпукло.

Если задача имеет решение, то всегда имеется по меньшей мере одна вершина, где достигается опти­мальное значение целевой функции.

Вся­кая допустимая область имеет конечное число вер­шин. Допустимая область в ЗЛП (если она не пуста) всегда имеет по меньшей мере одну вершину.

Для решения задач ЛП применяется различные модификации симплекс-метода.

В настоящее время разработано значительное количество программных продуктов, реализующих алгоритмы ЛП. - начиная от экселя и заканчивая специализироваными прикладными пакетами программ.