5 Варіант модульного контролю та зразок його виконання
Варіант МК
Частина перша (тестова)
1 Яка з даних функцій є явно заданою в декартовій системі координат хОу?
А) у
=
+ 1;
Б) y
=
+3;
В) r
= 5
;
Г)
.
2
Обчисліть
.
А) 8; Б) µ ; В) 0; Г) 4.
3
Функція
в точці
х
= 2
А) терпить усувний Б) терпить неусувний
розрив I роду; розрив I роду;
В) терпить розрив Г) є неперервною
I I роду;
4 Похідною функції y = f(x) у точці х є
А)
;
Б)
;
В)
;
Г)
(якщо
границя існує).
5
Обчисліть
,
якщо
.
А) 2х
+3; Б)
;
В)
;
Г) 2.
6 Якщо
в D
(f), то
функція f(x)
в D
(f)
А) монотонна;
Б) має точки розриву;
В) має екстремуми;
Г) стала.
7
Графік
функції
є:
А) всюди опуклим; Б) всюди угнутим;
В)
Г)
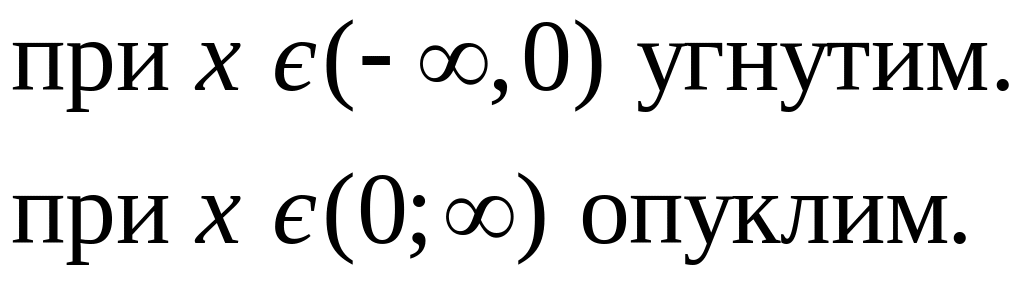
Частина друга
1
Достатня
умова зростання функції
на
проміжку(з доведенням).
2
Знайти
.
3 Знайти екстремуми функції:
Розв’язання:
Частина перша (тестова)
1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Б |
Б |
Г |
Г |
В |
А |
А |
2
(за
правилом Лопіталя)
=
.
3
, тобто
за означенням функція неперервна в
точці х = 2 .
4
(якщо границя існує).
5
.
6
Функція
f(x)
не
є сталою, оскільки її похідна залежить
від аргументу
.
>0
для
всіх
,
тобто
функція зростає в
і не має екстремуму.
7 .
,
;
>
0 при
,
тобто
графік функції
є
всюди опуклим.
Частина друга
1 Достатня умова зростання функції на проміжку.
Теорема.
Якщо
похідна диференційованої на проміжку
функції,
додатна
для
<
<
,
то
функція зростає на цьому проміжку.
Доведення.
Нехай
>
0, де
<
<
.
Розглянемо
будь-які значення
та
такі,
що
<
. За
теоремою Лагранжа про скінченні прирости
маємо:
де
За
умовою
>
0, звідси
випливає, що
>
0, а
це означає, що
–
зростаюча
функція.
Теорему доведено.
2 Знайти .
Перший спосіб:
=
.
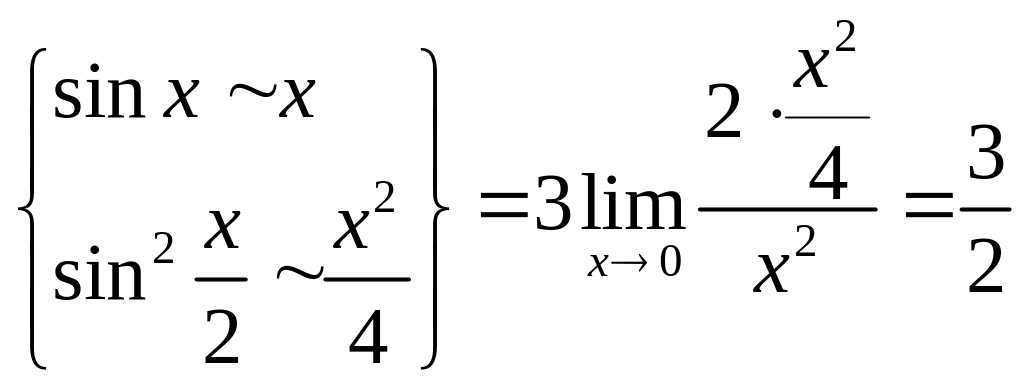Другий спосіб:
(
за правилом Лопіталя)
= =
=
.
3 Знайти екстремуми функції
>
0
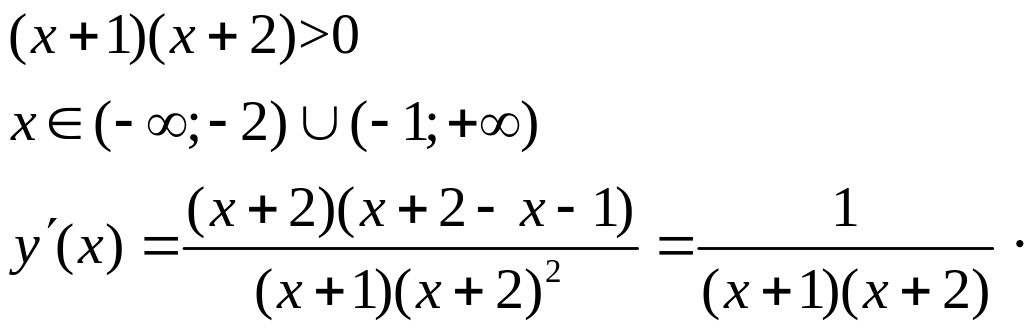
Критичних
точок функція не має, оскільки
>
0 при
,
тобто
функція скрізь зростає в області
визначення. Екстремумів функція не
має.
Для маємо:
Ох
6 Перелік тестових завдань
Варіант 1
1.1 Яка з даних функцій є явно заданою в декартовій системі координат хОу?
А) у = sin(xy) + 1; Б) y = +3; В) r = 5 cos ; Г) .
1.2 Яка з даних функцій є неявно заданою в декартовій системі координат хОу?
А) у
= cos(x+2y)
- 3;
Б) y
= x
+2;
В) r
= 3 cos
;
Г)
.
1.3 Яка з даних функцій є параметрично заданою?
А) у
= 3x
+ 1;
Б) y
=
+2; В)
r
=
; Г)
.
1.4.
Дано
функцію
. Знайдіть
f
(0).
А) 3; Б) -3; В) 0; Г) 4.
1.5 Визначте, які з наданих функцій є парними
А)
;
Б)
;
В)
;
Г)
.
1.6 Визначте, які з наданих функцій є не парними
А)
;
Б)
;
В)
;
Г)
.
1.7
Назвіть
координати точки перетину графіка
функції
з
віссю абсцис?
А) (0;1); Б) (1; 0); В) (1;1); Г) (0;0).
1.8
Назвіть координати точки перетину
графіка функції
з
віссю ординат?
А) (0;0); Б) (5; 0); В) (0;5); Г) (5;5).
1.9
Знайдіть
область визначення функції
.
А) (3; ); Б) 3; ); В) (-3; ); Г) (-; 3.
1.10
Знайдіть
область визначення функції
.
А) (2; );
Б)
2;
);
В)
(-;
2)
(2;
);
Г)
(-;
2.
2.1 Обчисліть .
А) 8; Б) ; В) 0; Г) 4.
2.2
Обчисліть
.
А)
2; Б)
; В)
; Г)
0.
2.3
Обчисліть
.
А) 8; Б) +µ ; В) 3; Г) 4.
2.4
Обчисліть
.
А)
3; Б)
; В)
; Г)
1.
2.5
Обчисліть
.
А)
; Б)
; В)
3; Г)
.
2.6
Обчисліть
.
А) 8; Б) ; В) 0; Г) 3.
2.7
Обчисліть
.
А) 3; Б) ; В) 0; Г) 5.
2.8
Обчисліть
.
А) 3; Б) ; В) 0; Г) 3.
2.9
Обчисліть
.
А) 8; Б) ; В) 0; Г) 4.
2.10
Обчисліть
.
А) 5; Б) +µ ; В) 2; Г) 0.
3.1 Функція у точці х = 2
А) терпить усувний Б) терпить неусувний
розрив I роду; розрив I роду;
В) терпить розрив Г) є неперервною.
I I роду;
3.2
Функція
у
точці
х = 3
А) терпить усувний Б) терпить неусувний
розрив I роду; розрив I роду;
В) терпить розрив Г) є неперервною.
I I роду;
3.3
Функція
в точке х =
0
А) терпить усувний Б) терпить неусувний
розрив I роду; розрив I роду;
В) терпить розрив Г) є неперервною.
I I роду;
3.4
Функція
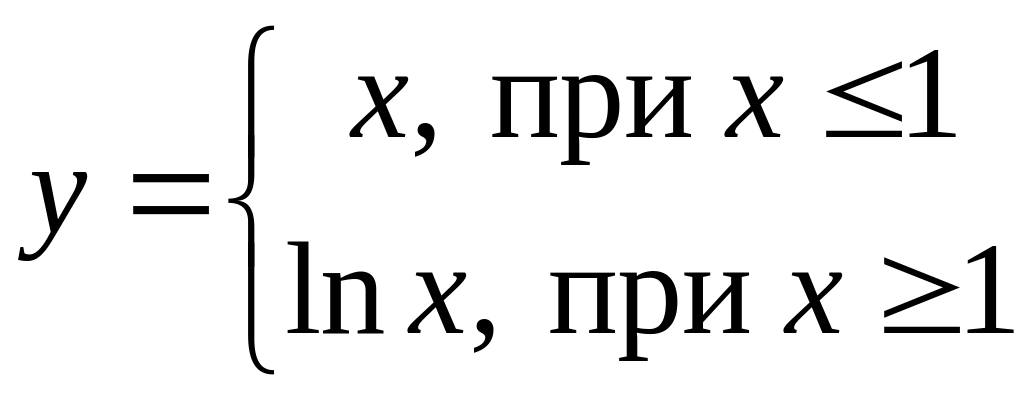в точці
х = 1
А) терпить усувний Б) терпить неусувний
розрив I роду; розрив I роду;
В) терпить розрив Г) є неперервною;
I I роду;
3.5 З наданих функцій
1)
; 2)
; 3)
; 4)
; 5)
неперервними в точці х = 3 є:
А) 1; 2; 5; Б) 1;2;3; В) 1;3;4; Г) 1; 3;5.
3.6 З наданих функцій
1)
; 2)
; 3)
; 4)
; 5)
.
еквівалентними
нескінченно малими при
є:
А) 1 і 3; Б) 2 і 4; В) 3 і 5; Г) 1 і 4.
3.7
Якщо
, то
функція у
= f(x)
у
точці х
= а є:
А) нескінченно великою; Б) нескінченно малою;
В) обмеженою; Г) сталою.
3.8
Якщо
, то
функція у
= f(x)
у
точці х
= а є:
А) нескінченно великою; Б) нескінченно малою;
В) необмеженою; Г) обов'язково неперервною.
3.9 Які з пар функцій f(x) і g(x) є еквівалентними нескінченно малими
при ?
А)
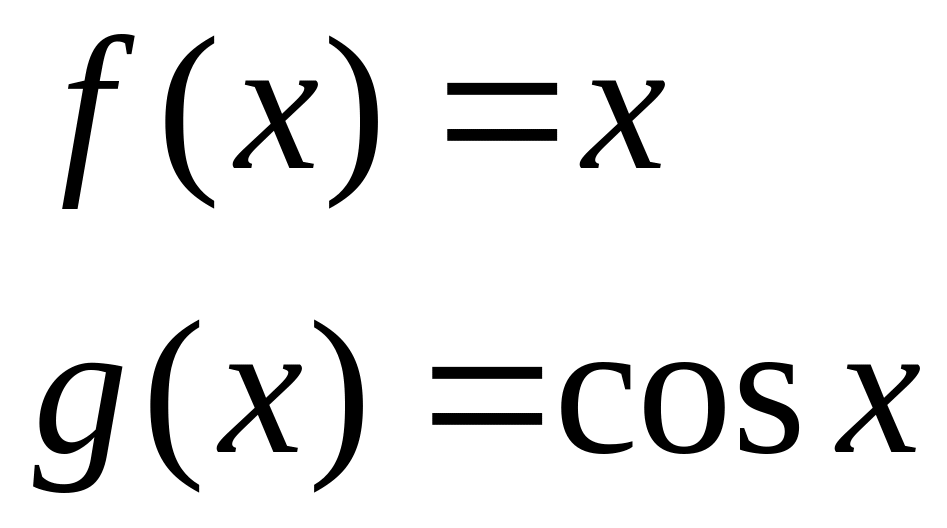; Б)
; В)
; Г)
.
3.10 Будь-яка неперервна на [a; b ] функція f(x) :
А) диференційована на [a; b ] ; В) обмежена на [a; b ] ;
Б) має корінь на [a; b ] ; Г) монотонна на [a; b ]
4.1 Похідною функції y = f(x) у точці х є:
А) ; В) ;
Б) ; Г) ( якщо границя існує).
4.2 Якщо u(x) і v(x) - диференційовані в точці х, то похідна їх добутку обчислюється за формулою:
А)
; Б)
;
В)
; Г)
.
4.3 Якщо u(x) та v(x) - диференційовані в точці х, то похідна їх частки обчислюється за формулою:
А)
; В)
;
Б)
; Г)
.
4.4
Кутовий
коефіцієнт дотичної до графіка функції
в
точці
х
= 0 дорівнює:
А) 1; Б)
; В)
5; Г) 0.
4.5 Шлях,
пройдений тілом, заданий рівнянням
(м).
Знайдіть
швидкість тіла через 2 секунди після
початку руху.
А) 2 м/с; Б) 28 м/с; В) 14 м/с; Г) 10 м/с.
5.1
Обчисліть
,
якщо
.
А) 2х
+3; Б)
; В)
; Г)
2.
5.2
Обчисліть
,
якщо
.
А) 2х
+3; Б)
; В)
; Г)
2.
5.3
Обчисліть
,
якщо
.
А) 3х
+3; Б)
; В)
; Г)
2х-7.
5.4
Обчисліть
,
якщо
.
А)
2х; Б)
3х; В)
3
; Г)
1.
5.5
Обчисліть
диференціал
функції
.
А) 15х
; Б)
; В)
; Г)
0.
6.1
Якого
найменшого значення набуває функція
на
відрізку -1; 1?
А) 0; Б) 1; В) –1; Г) –2.
6.2
Якого
найбільшого значення набуває функція
на
відрізку -1; 1?
А) 0; Б) 1; В) –1; Г) –2.
6.3 Якщо в D (f), то функція f(x) в D (f):
А) монотонна; В) має екстремуми;
Б) має точки розриву; Г) стала.
6.4
Для
функції
точка
х
= 0
є:
А) точкою максимуму; Б) точкою мінімуму;
В) точкою розриву; Г) критичною, але не екстремальною .
6.5
Функція
для всіх дійсних
чисел є:
А) сталою; Б) зростаючою;
В) спадаючою; Г) незростаючою.
6.6
Функція
для всіх дійсних
чисел
є:
А) сталою; Б) зростаючою;
В) спадаючою; Г) неспадаючою.
6.7 Для
функції
точка х
= 0
є:
А) точкою максимуму; Б) точкою мінімуму;
В) точкою розриву; Г) критичною, але не екстремальною .
6.8
Функція
на
проміжку (0;)
є:
А) сталою; Б) зростаючою в О.В.;
В) спадаючою в О.В.; Г) неспадаючою в О.В.
6.9
Для функції
точка х
= 0
є:
А) точкою максимуму; Б) точкою мінімуму;
В) точкою розриву; Г) критичною, але не екстремальною .
6.10
Знайдіть критичні точки функції
.
А) х = 1; Б) х = 0;
В) х = -2; Г) критичних точок не має.
7.1 Графік функції є:
А) скрізь опуклим; Б) скрізь угнутим;
В)
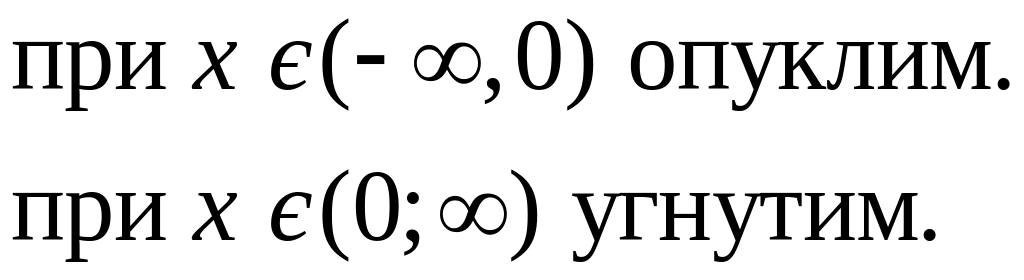Г)
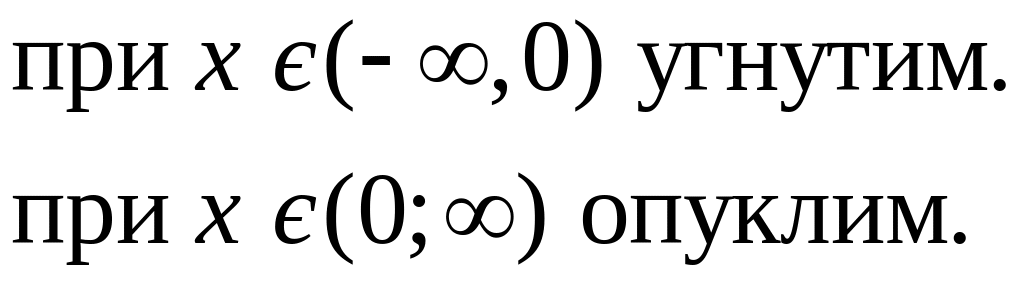
7.2 Графік
функції
є:
А) скрізь опуклим; Б) скрізь угнутим;
В)
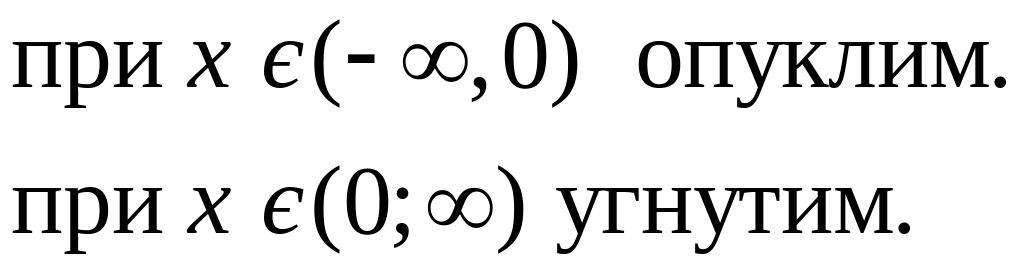Г)
.
7.3 Для функції точка х = 0 є:
А) точкою перегину; Б) точкою мінімуму;
В) точкою розриву; Г) точкою максимуму.
7.4 Для якої з даних функцій пряма х = 2 є вертикальною асимптотою?
А)
; Б)
; В)
; Г
)
.
7.5 Яка з даних функцій не має вертикальних асимптот?
А)
; Б)
; В)
; Г)
.