
- •1 Програма модуля
- •Введення в математичний аналіз
- •Диференціальне числення функції однієї змінної
- •1.3 Дослідження функцій за допомогою похідних
- •2 Варіанти індивідуальних домашніх завдань
- •3 Варіанти підсумкового завдання
- •4 Зразок виконання підсумкового завдання
- •5 Варіант модульного контролю та зразок його виконання
- •6 Перелік тестових завдань
- •7 Питання для самопідготовки
- •7.1 Введення в аналіз
- •7.2 Диференціальне числення функції однієї змінної
- •7.3 Дослідження функції за допомогою похідної
- •Список джерел інформації
- •1 Програма модуля…………………………………………………………………3
- •Навчальне видання
Міністерство освіти і науки
України
Х АРКІВСЬКИЙ
ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
БУДІВНИЦТВА І АРХІТЕКТУРИ
АРКІВСЬКИЙ
ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ
БУДІВНИЦТВА І АРХІТЕКТУРИ
Спеціальності: 6.060101
6.060103
6.050503
6.050202
6.040106
МЕТОДИЧНІ ВКАЗІВКИ
ДО ВИКОНАННЯ ЗАВДАНЬ МОДУЛЯ
“ВВЕДЕННЯ В АНАЛІЗ. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ”
з курсу “Вища математика”
Харків 2008
ВСТУП
Пропоновані методичні вказівки призначені для надання допомоги студентам в організації самостійної роботи за темами “ Введення в аналіз і диференціальне числення функції однієї змінної ”.
Результативність самостійної роботи забезпечується системою контролю, яка включає наступні етапи:
виконання індивідуальних домашніх завдань;
виконання контрольної роботи на тему “ Похідна функції ”;
виконання і складання підсумкового завдання на тему “ Дослідження
функції за допомогою похідної ”;
виконання модульної контрольної роботи з усієї теми модуля.
Методичні вказівки містять робочу програму модуля, індивідуальні домашні завдання, варіанти підсумкового завдання і зразок його виконання, а також варіанти тестових завдань, зразок виконання модульного контролю і питання для підготовки до його складання.
1 Програма модуля
Введення в математичний аналіз
Поняття функції, способи її задання. Основні елементарні функції.
Границя змінної величини, границя функції в точці. Властивості
функцій, що мають границю.
3 Нескінченно малі і нескінченно великі, їх властивості і зв'язок між ними.
4 Порівняння нескінченно малих. Еквівалентні нескінченно малі. Їх використання під час обчисленні границь.
5 Перша та друга чудові границі.
6 Неперервність функції в точці та на відрізку. Властивості функцій неперервних на відрізку.
7 Односторонні границі. Точки розриву функції і їх класифікація.
Диференціальне числення функції однієї змінної
1 Задачі, що приводять до поняття похідної. Похідна функції, її геометричний та механічний сенс. Похідні суми, добутку та відношення функцій .
2 Похідна складної функції. Похідна оберної функції. Таблиця похідних.
3 Похідна неявної функції і функції, заданої параметрично. Правило логарифмічного диференціювання.
4 Диференційованість функції. Диференціал функції. Зв'язок диференціала з похідною. Геометричний сенс диференціала.
Похідні та диференціали вищих порядків.
Теореми Ролля, Лагранжа та Коші. Правило Лопіталя.
7 Дотична і нормаль до кривої; кривизна кривої.
1.3 Дослідження функцій за допомогою похідних
1 Умови зростання та спадання функції. Точки екстремуму. Необхідні і достатні ознаки існування екстремуму. Знаходження найбільшого і найменшого значень неперервної на відрізку функції.
2 Дослідження функцій на екстремум за допомогою похідних вищих порядків.
3 Необхідні і достатні умови опуклості й угнутості функції та точок перегину.
4 Асимптоти кривої та загальна схема побудови графіків.
2 Варіанти індивідуальних домашніх завдань
Завдання 1. Знайти границі, використовуючи еквівалентні нескінченно малі
функції
(![]() -
номер варіанта).
-
номер варіанта).
1.
![]() 4.
4.
![]()
2.
![]() 5.
5.
![]() 7.
7.
![]()
3.
![]() 6.
6.
![]()
Завдання 2. Знайти границі функцій ( - номер варіанта).
1.
![]() 6.
6.
![]()
2.
![]() 7.
7.
![]()
3.
![]() 8.
8.
![]()
4.
![]() 9.
9.
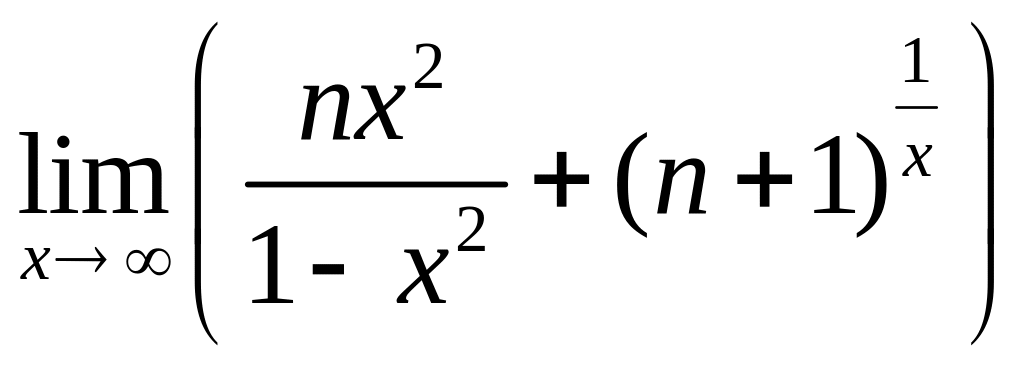
5.
![]() 10.
10.
![]()
Завдання 3. а) Дослідити на неперервність функції та побудувати їх графіки.
б) Дослідити на неперервність функцію в точках х1, х2.
Варіант № 1 Варіант № 2
а)
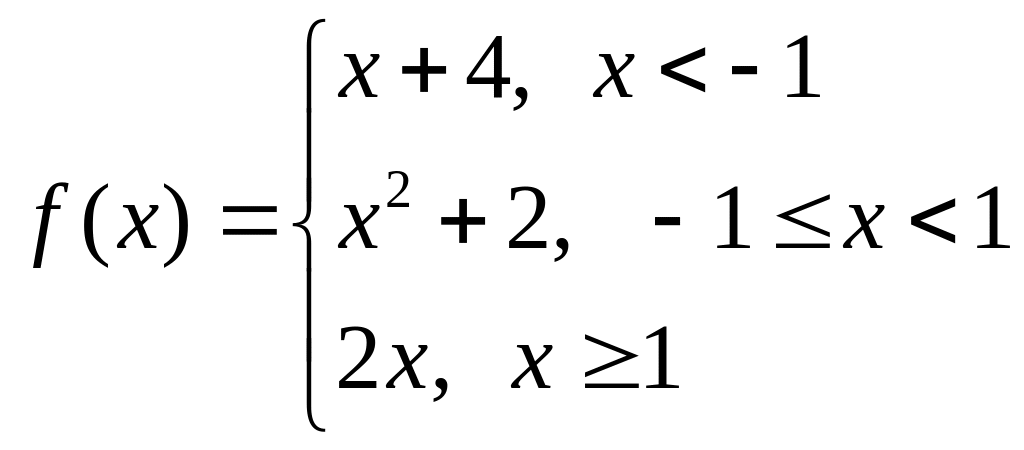 а)
а)
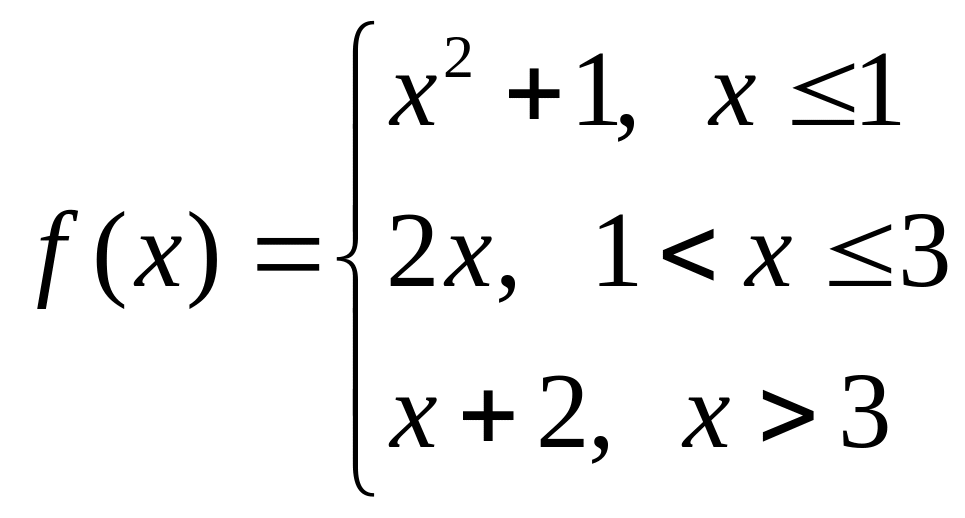
б)
![]() б)
б)
![]()
Варіант № 3 Варіант № 4
а)
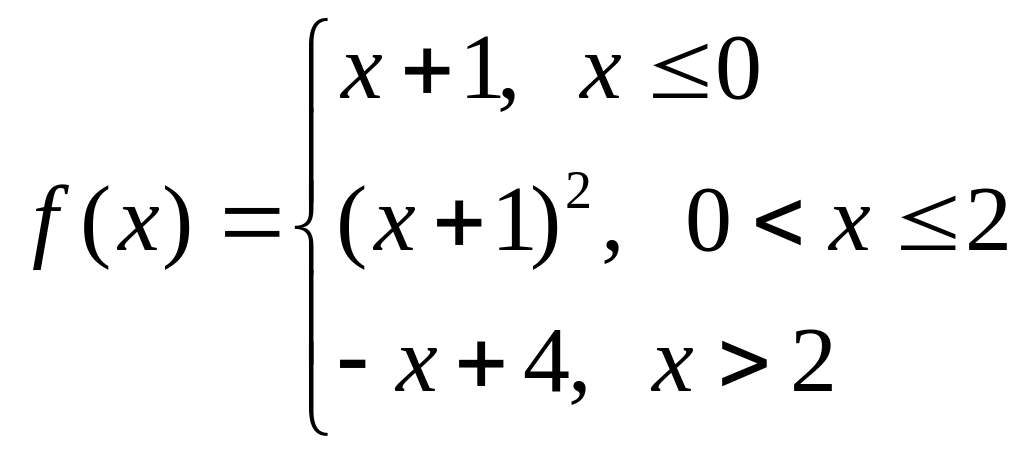 а)
а)
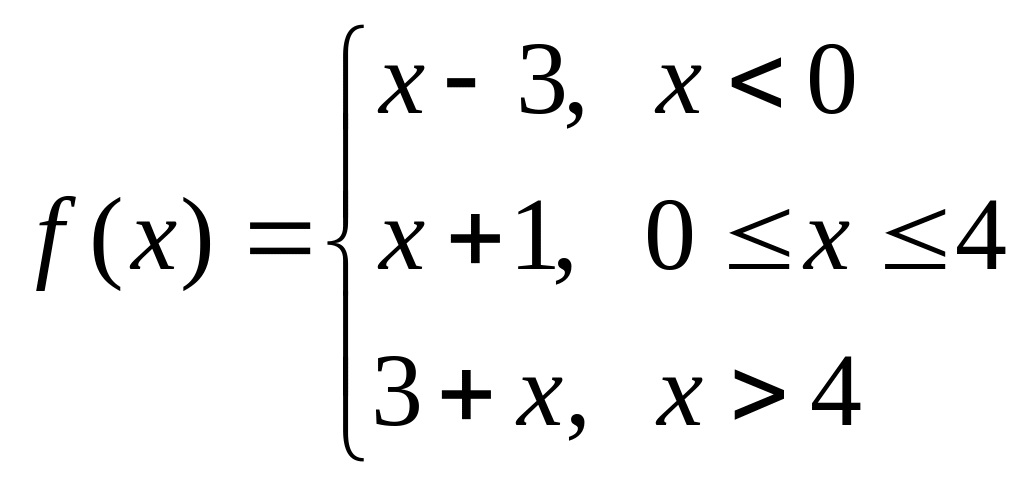
б)
![]() б)
б)
![]()
Варіант № 5 Варіант № 6
а)
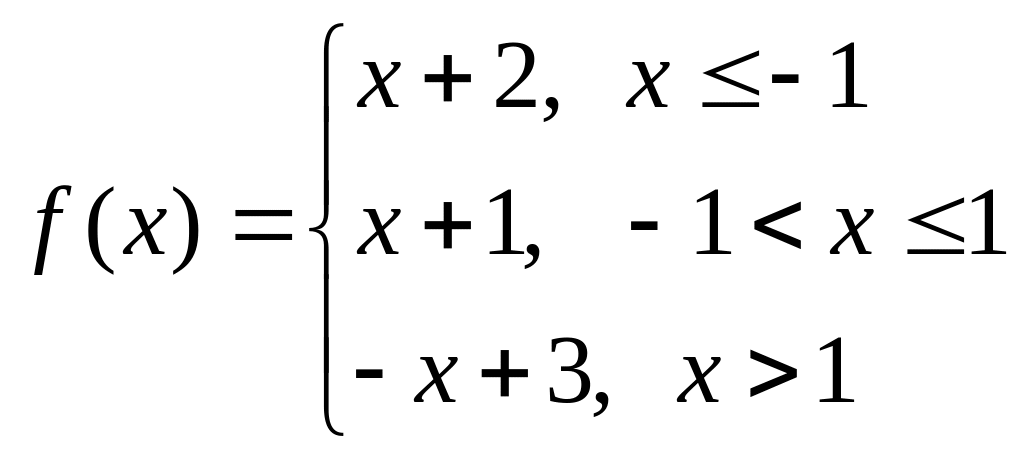 а)
а)
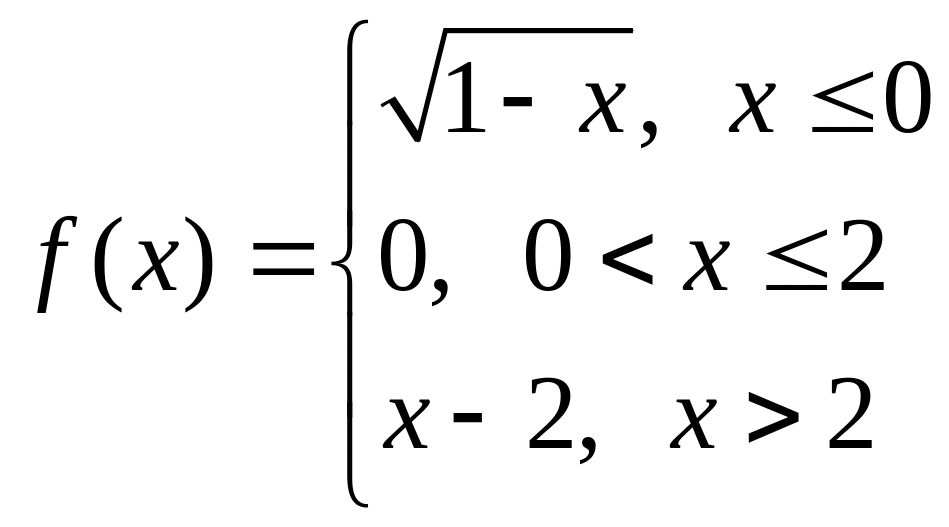
б)
![]() б)
б)
![]()
Варіант № 7 Варіант № 8
а)
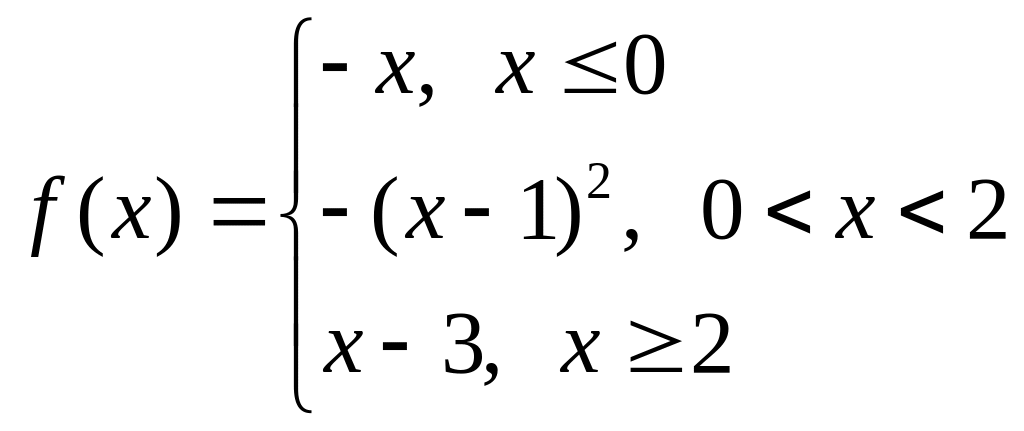 а)
а)
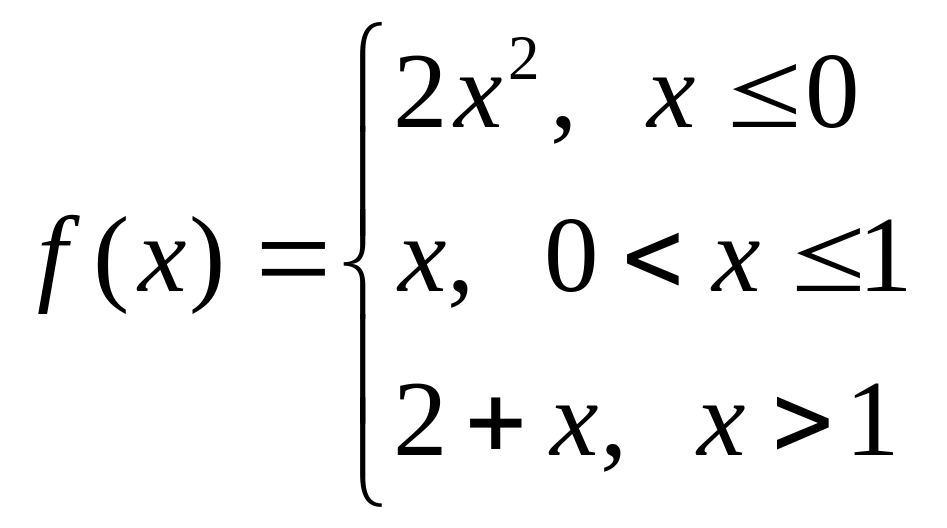
б)
![]() б)
б)
![]()
Варіант № 9 Варіант № 10
а)
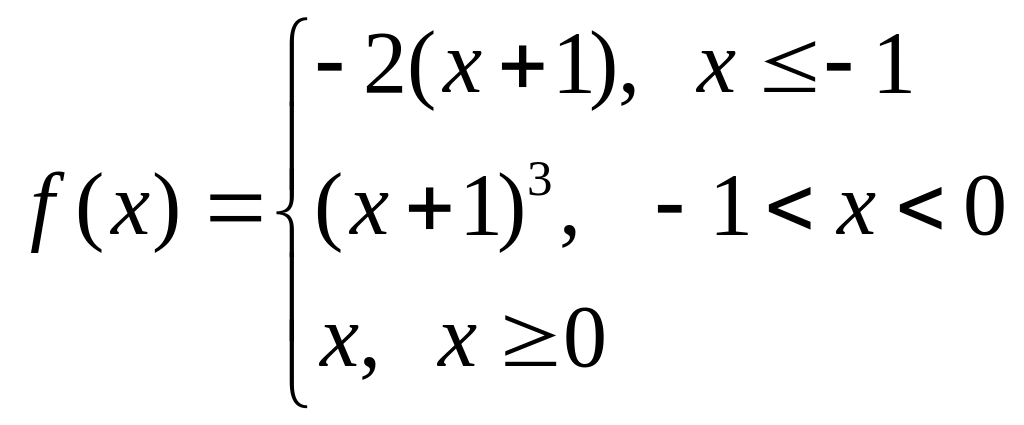 а)
а)
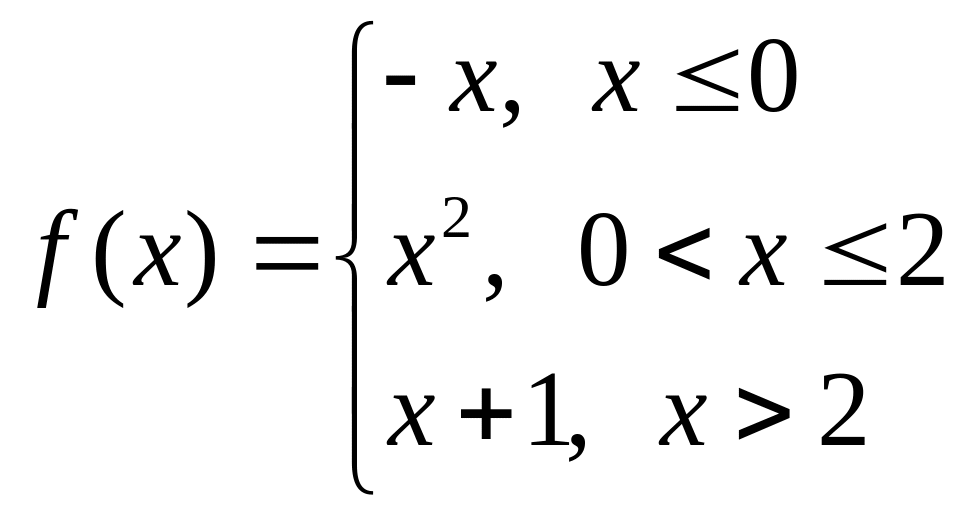
б)
![]() б)
б)
![]()
Варіант № 11 Варіант № 12
а)
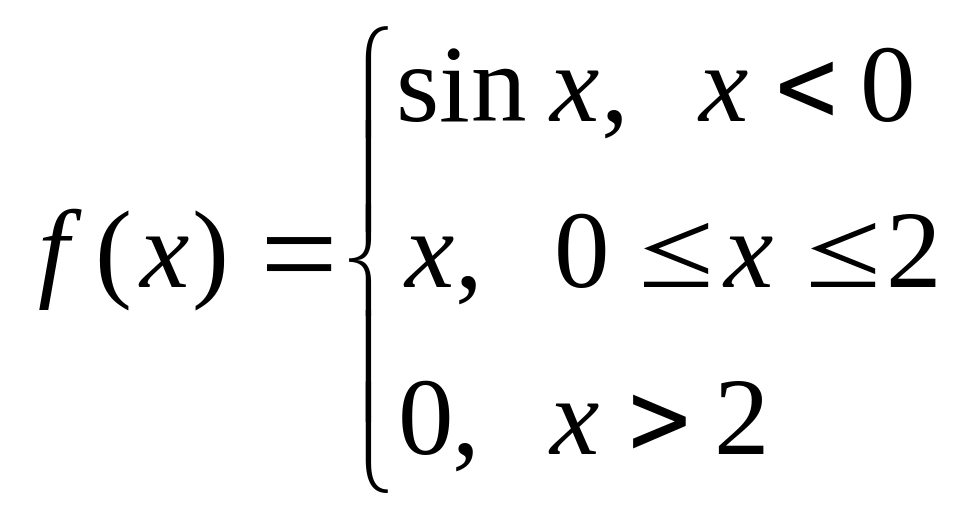 а)
а)
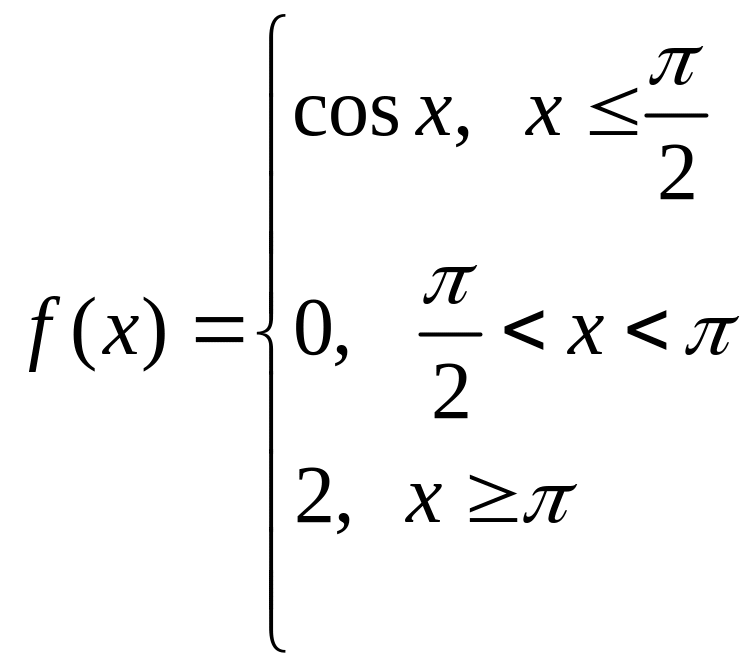
б)
![]() б)
б)
![]()
Варіант № 13 Варіант № 14
а)
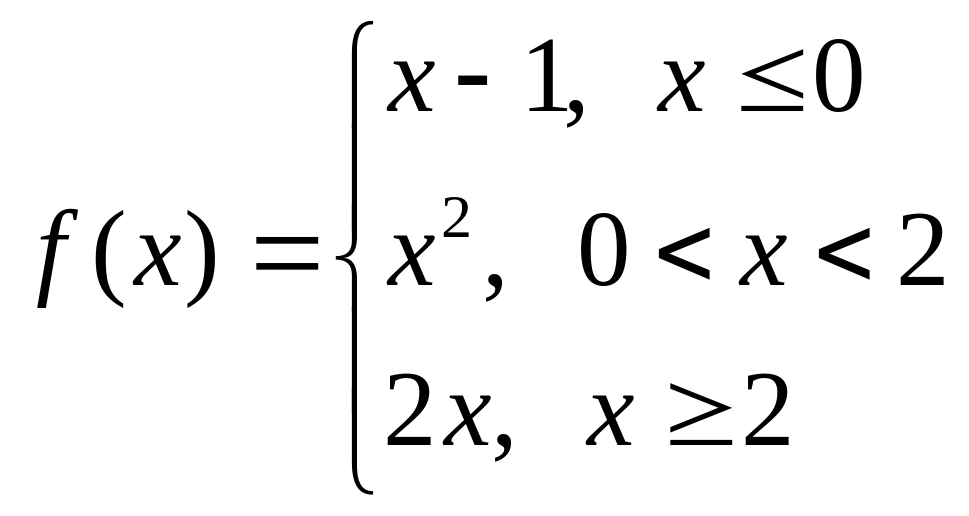 а)
а)
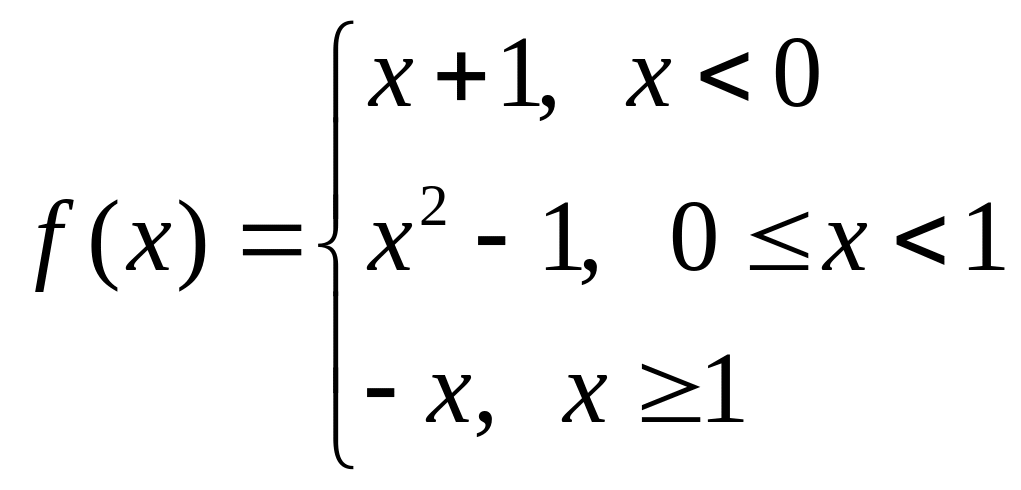
б)
![]() б)
б)
![]()
Варіант № 15 Варіант № 16
а)
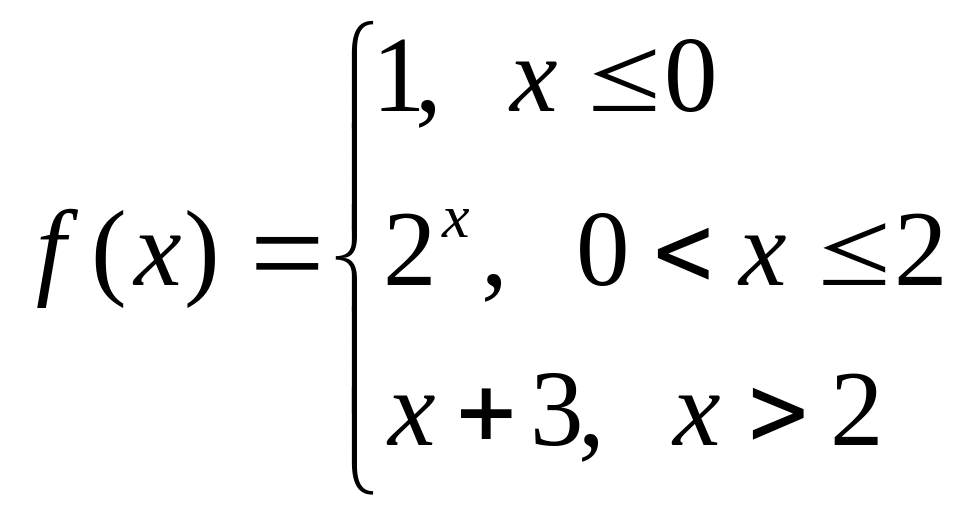 а)
а)
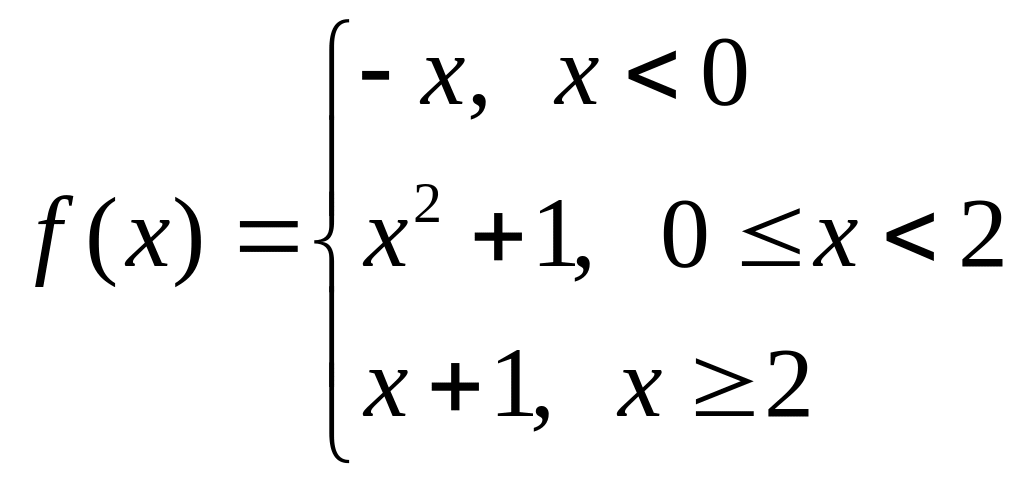
б)
![]() б)
б)
![]()
Варіант № 17 Варіант № 18
а)
 а)
а)
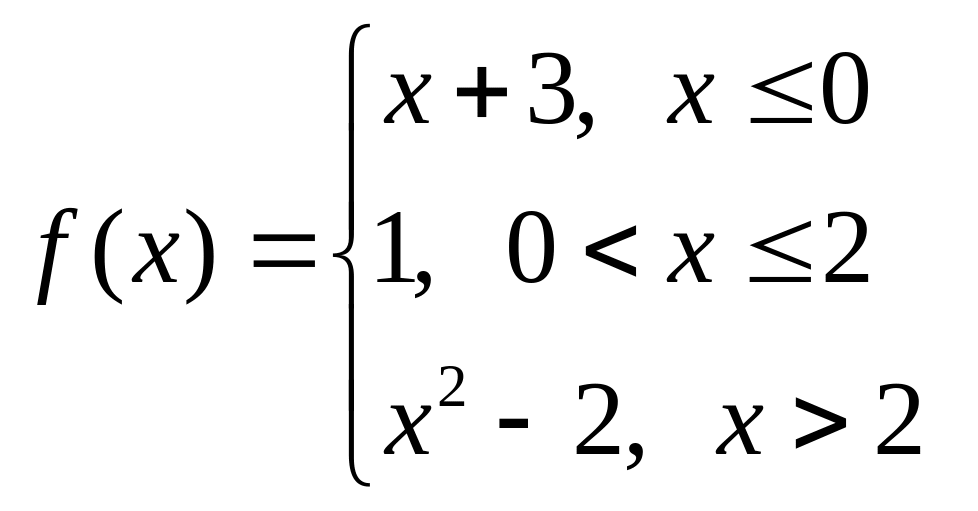
б)
![]() б)
б)
![]()
Варіант № 19 Варіант № 20
а)
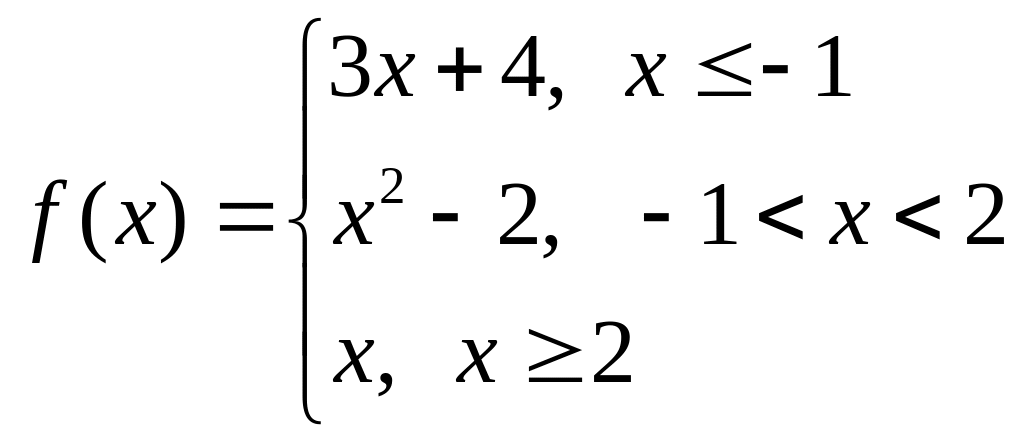 а)
а)
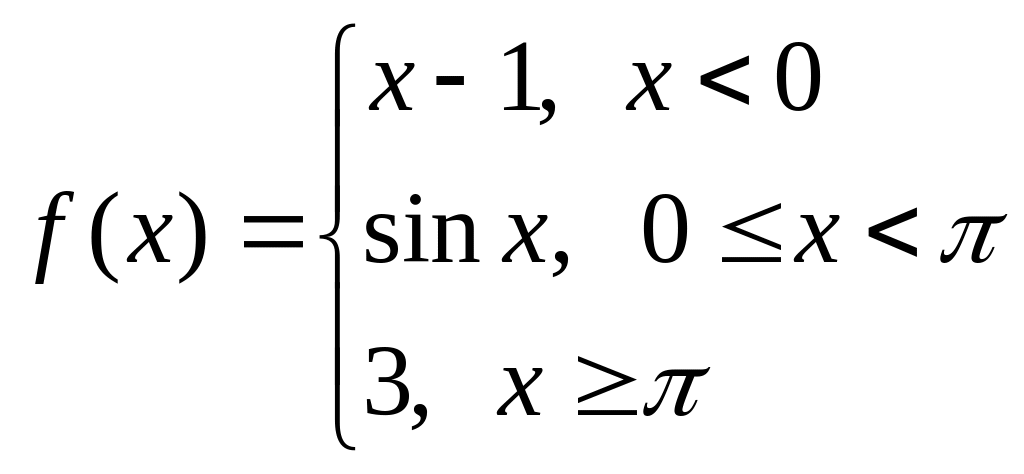
б)
![]() б)
б)
![]()
Варіант № 21 Варіант № 22
а)
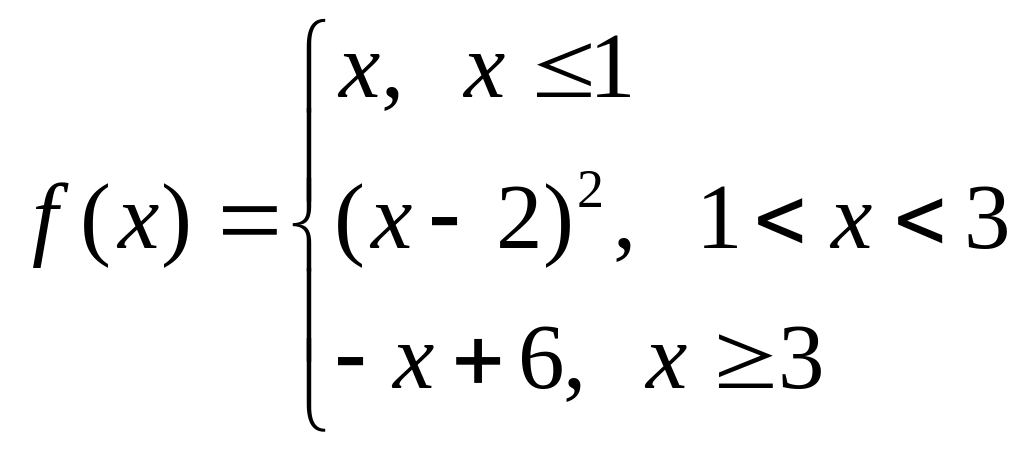 а)
а)
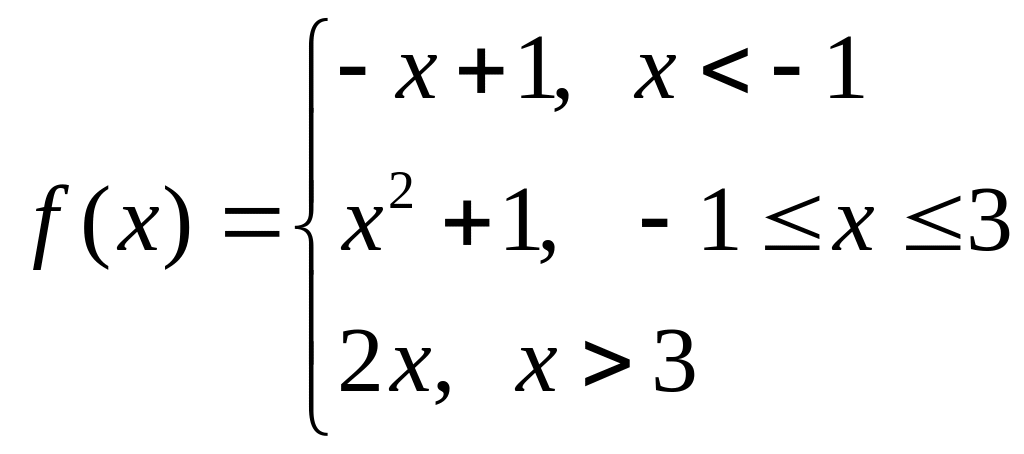
б)
![]() б)
б)
![]()
Варіант № 23 Варіант № 24
а)
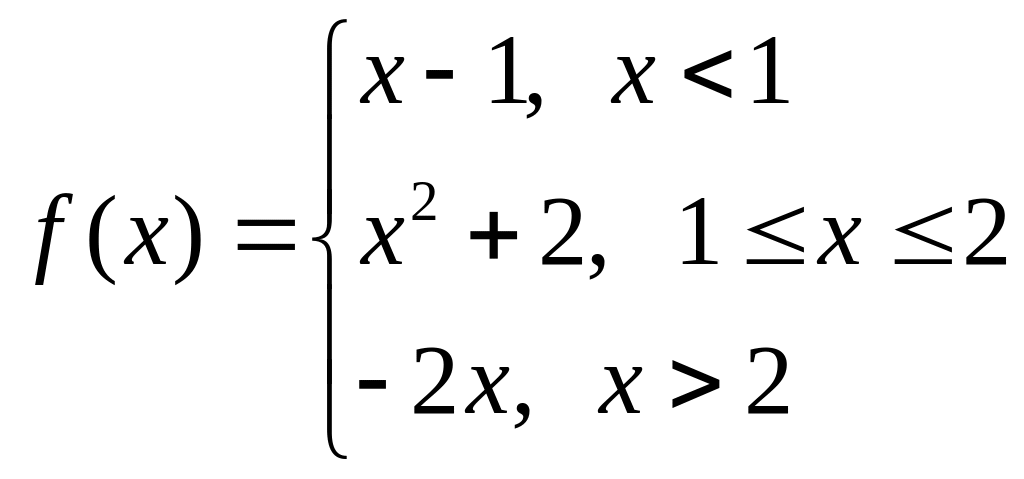 а)
а)
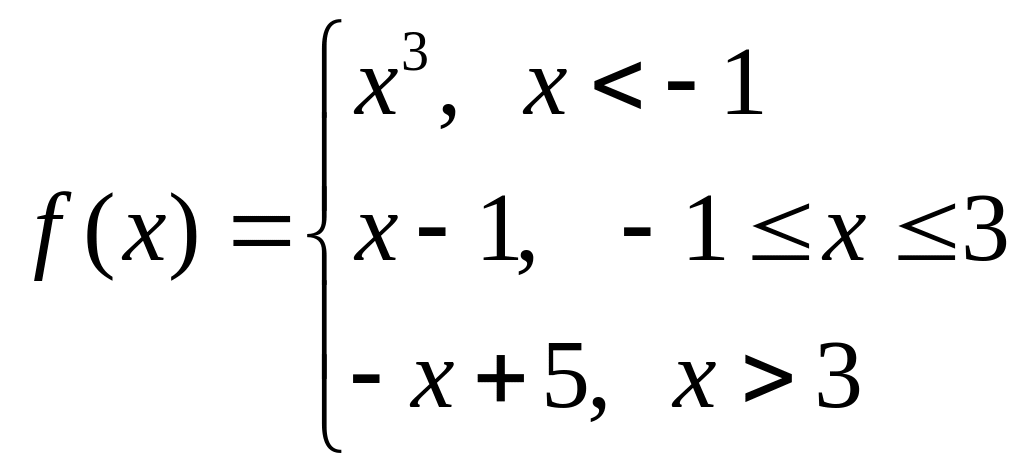
б)
![]() б)
б)
![]()
Варіант № 25 Варіант № 26
а)
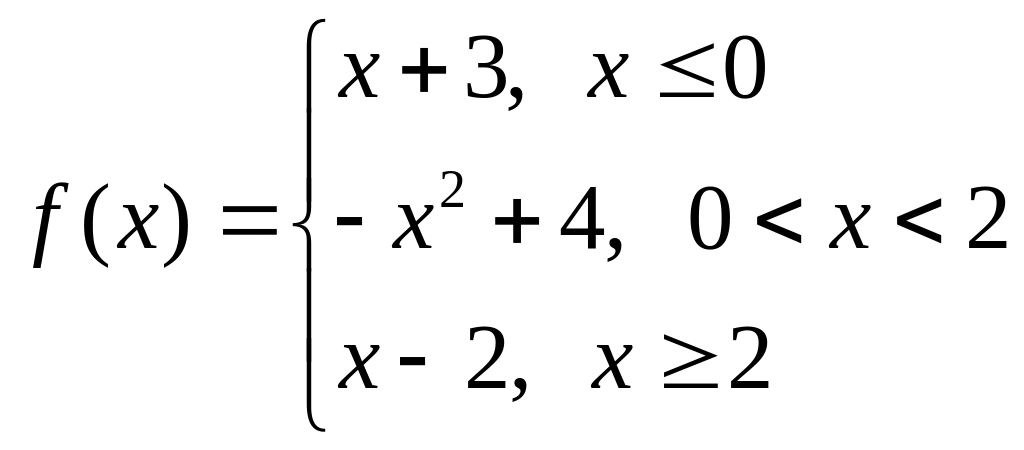 а)
а)
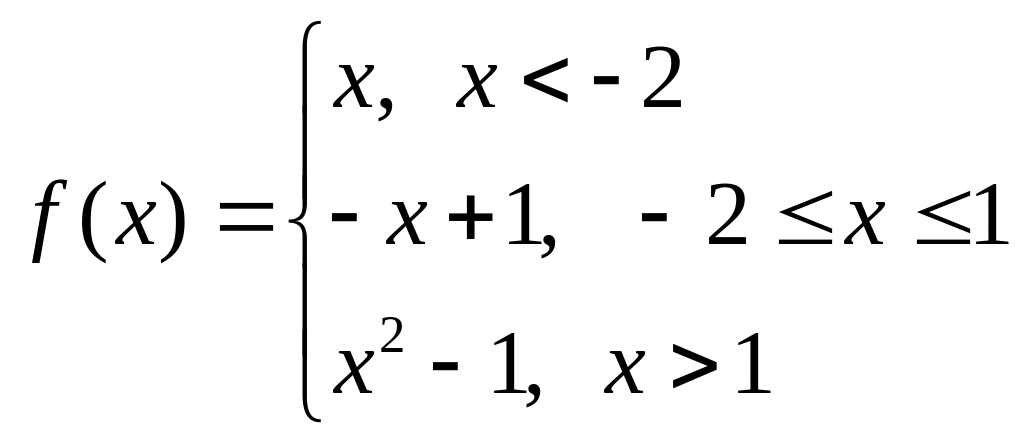
б)
![]() б)
б)
![]()
Варіант № 27 Варіант № 28
а)
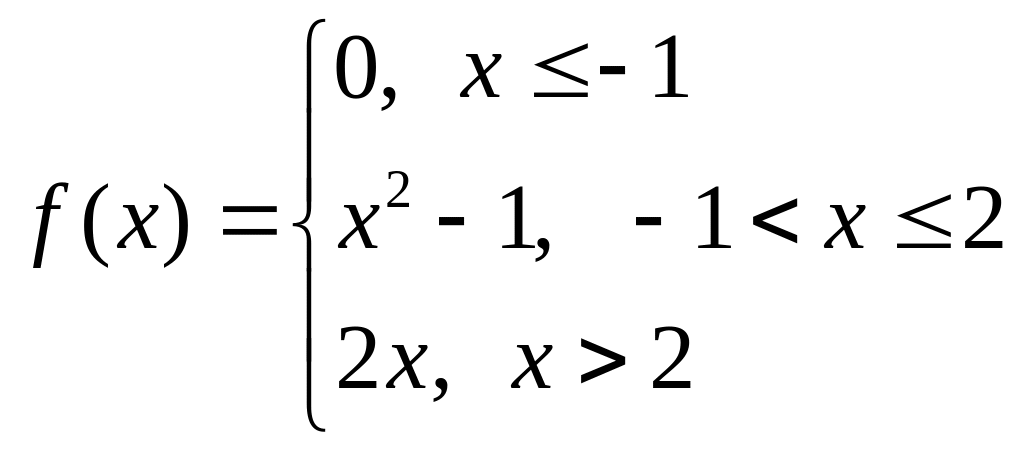 а)
а)
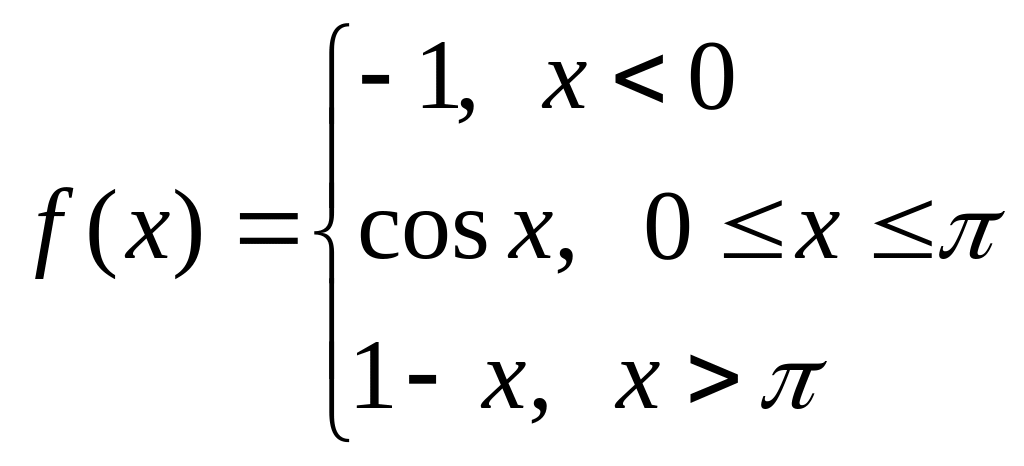
б)
![]() б)
б)
![]()
Варіант № 29 Варіант № 30
а)
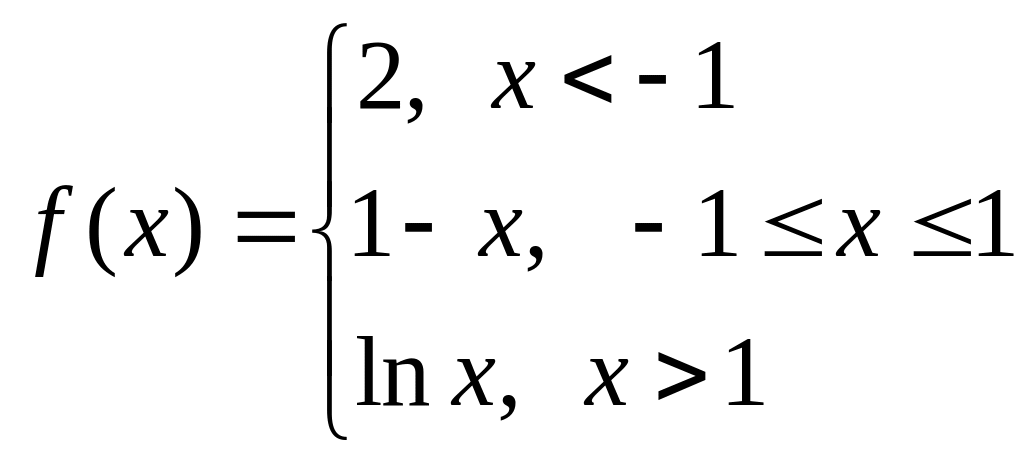 а)
а)
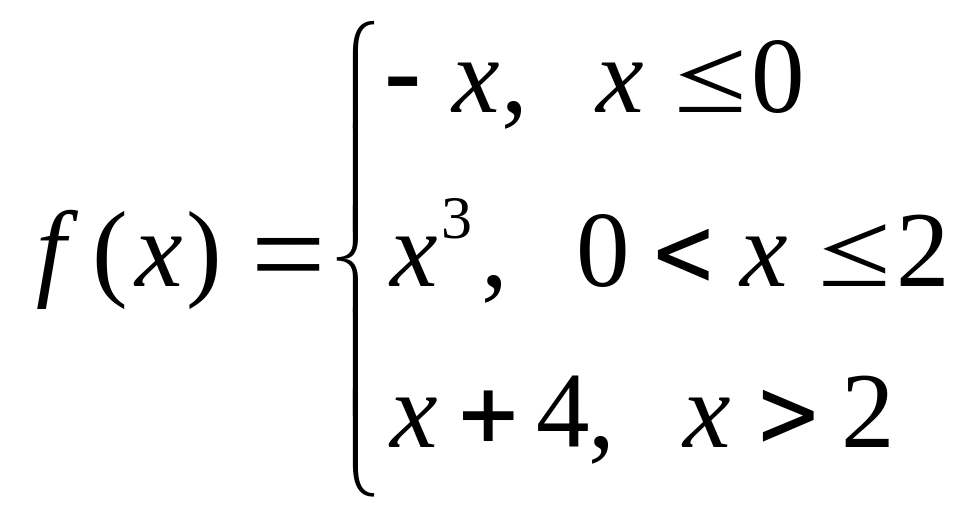
б)
![]() б)
б)
![]()
Завдання 4. Знайти похідні від заданих функцій.
Варіант № 1
1. S(t)
=
![]() 6.
y
=
6.
y
=
![]()
2.
![]() =
=![]() 7.
y
=
7.
y
=
![]()
3. y
=
![]() 8.
y
=
8.
y
=
![]()
4. y
=
![]() 9.
y
=
9.
y
=
![]()
5. y
= (![]() )
)![]() 10.
f(t)
=
10.
f(t)
=![]()
Варіант № 2
1. y
=
![]() 6.
y
= 5
6.
y
= 5![]()
2. y
=
![]() 7.
y
=
7.
y
=
![]()
3. y
=
![]() 8.
S(t)
=
8.
S(t)
=
![]()
4. y
=
![]() 9.
y
= 3
9.
y
= 3![]()
5. y
=
![]() 10.
y
=
10.
y
=
![]()
Варіант № 3
1. y
=
![]() 6.
y
=
6.
y
=
![]()
2. y
=
![]() 7.
y
=
7.
y
=
![]()
3. y
=
![]() 8.
y
=
8.
y
=
![]()
4. y
=
![]() 9.
y
=
9.
y
=
![]()
5. y
=
![]() 10.
S(t)
= 3
10.
S(t)
= 3![]()
Варіант № 4
y =
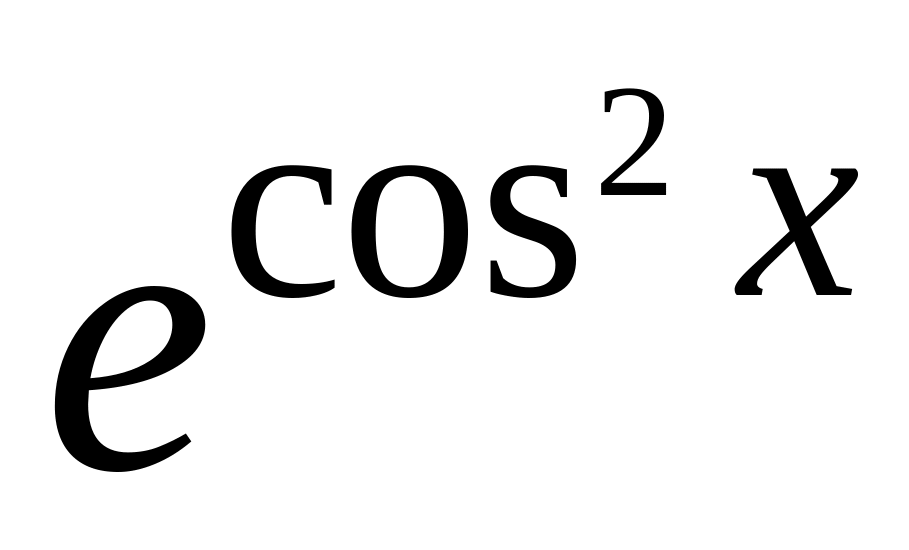 6.
f(t)
=
6.
f(t)
=
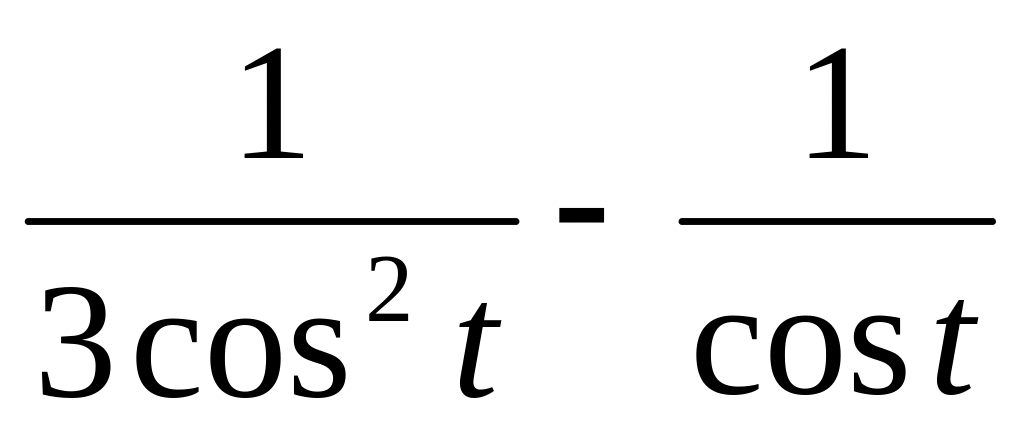
y =
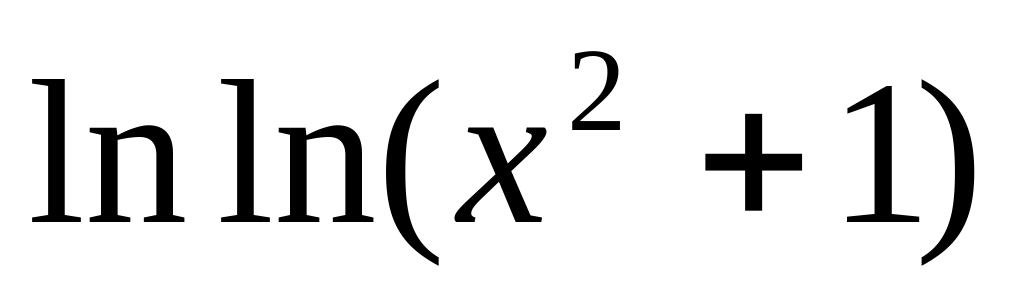 7.
y
=
7.
y
=
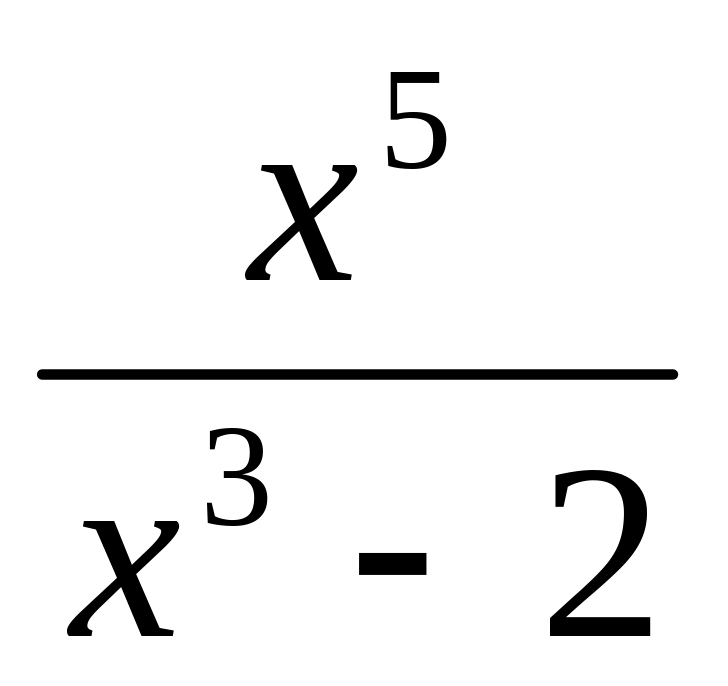
y =
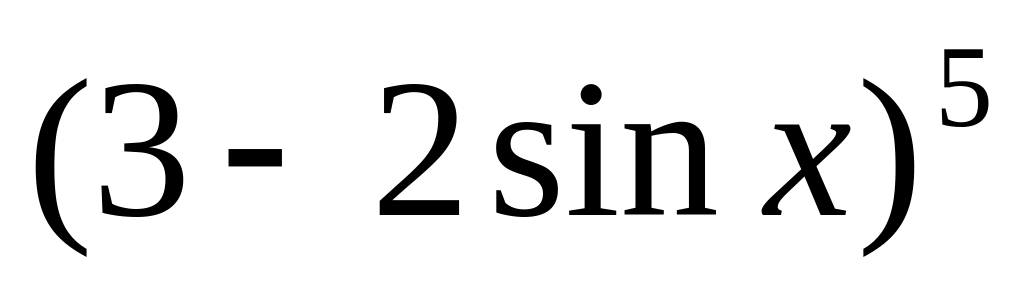 8.
z(t)
=
8.
z(t)
=

y =
 9.
y
=
9.
y
=
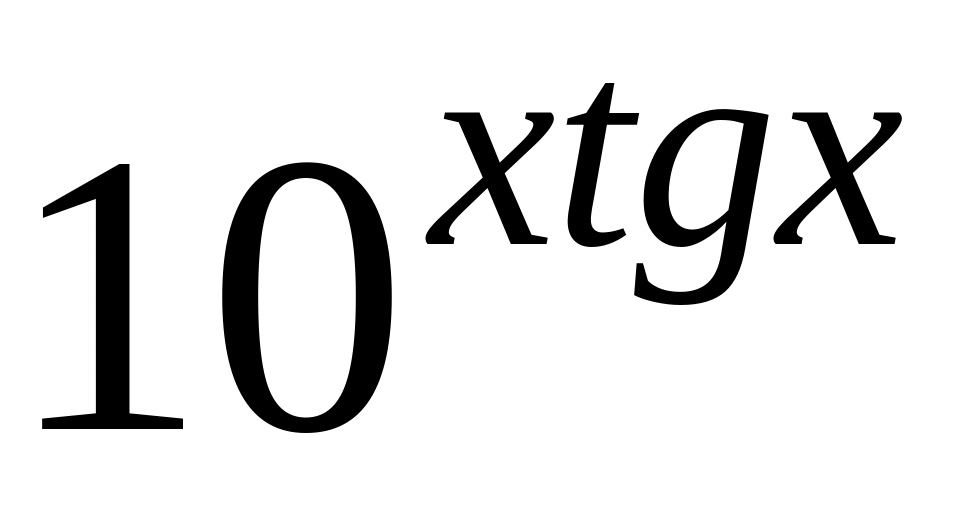
y =
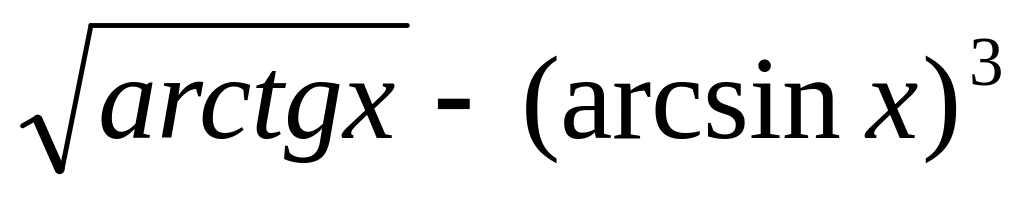 10.
y
= 5
10.
y
= 5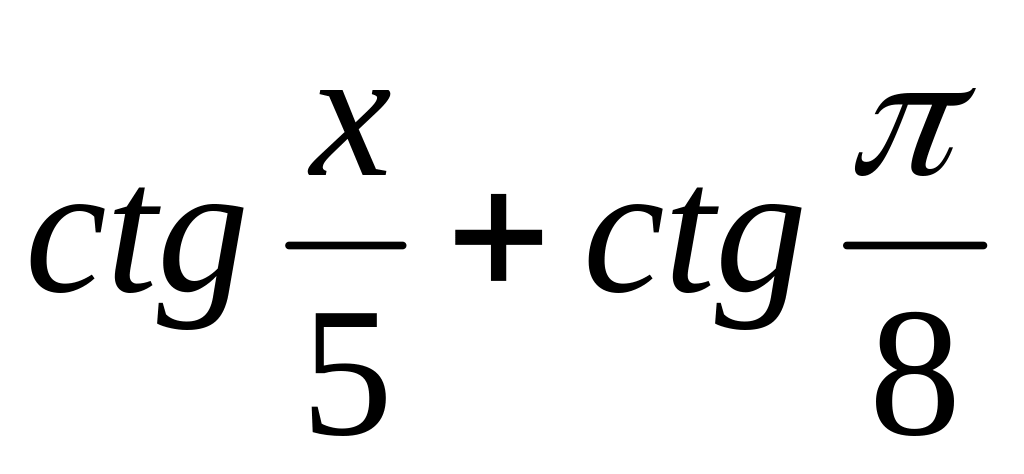
Варіант № 5
S(t) =
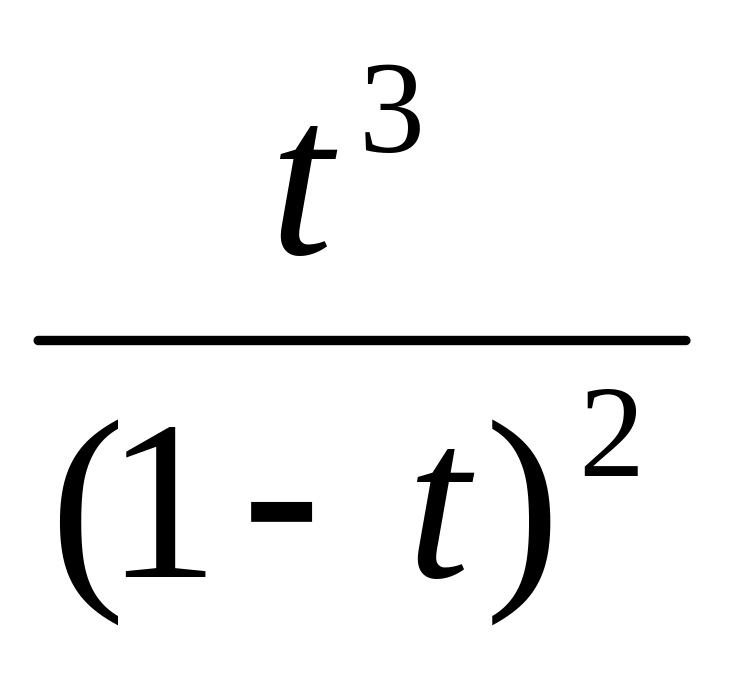 6.
y
=
6.
y
=

y = 3
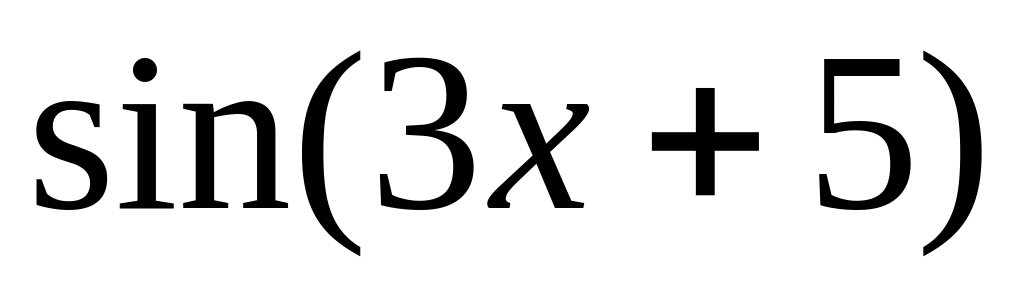 7.
y
=
7.
y
=

y =
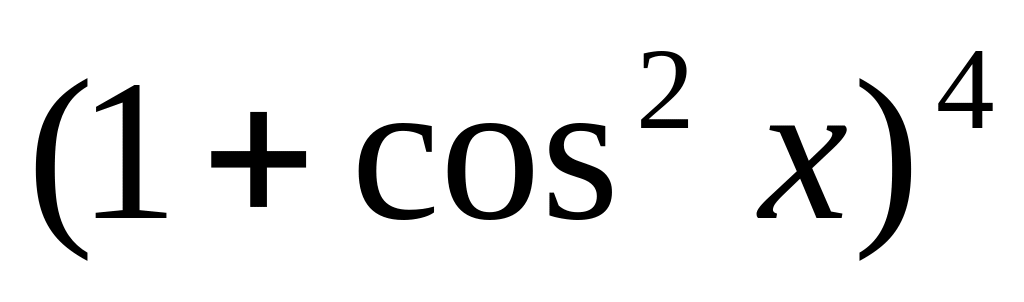 8.
y
=
8.
y
=
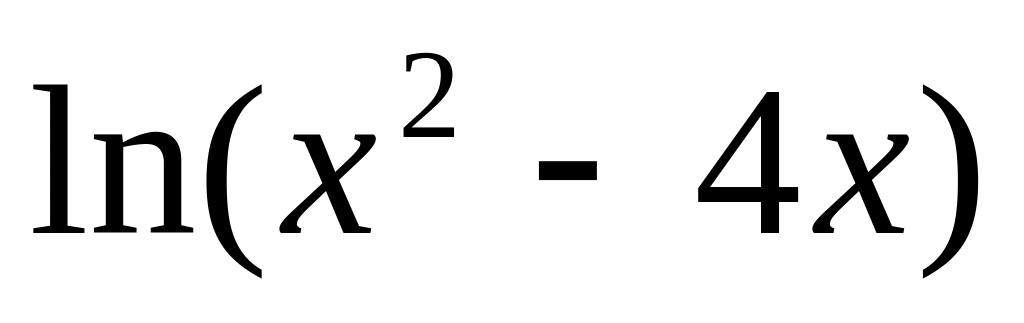
y =
 9.
y
=
9.
y
=

y =
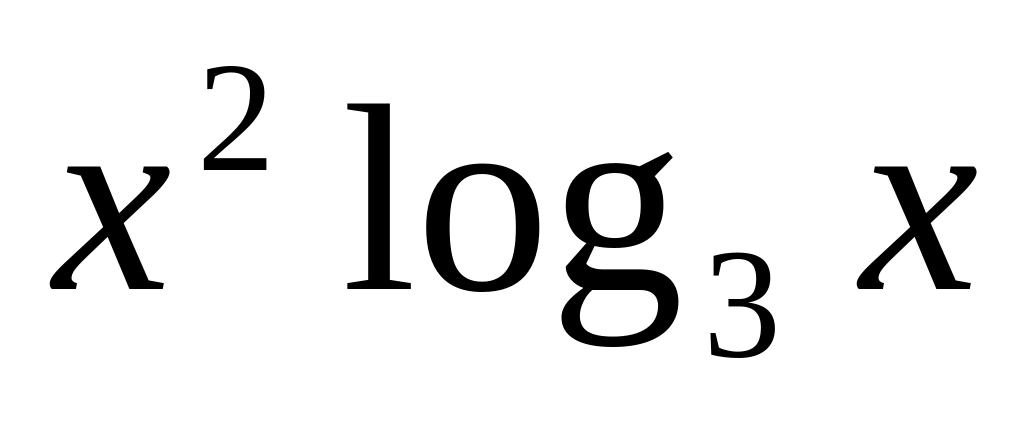 10.
y
= 5
10.
y
= 5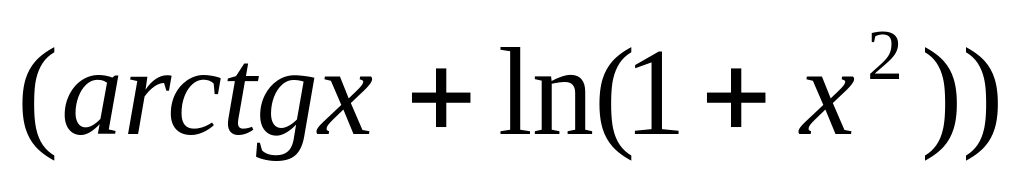
Варіант № 6
y = 5
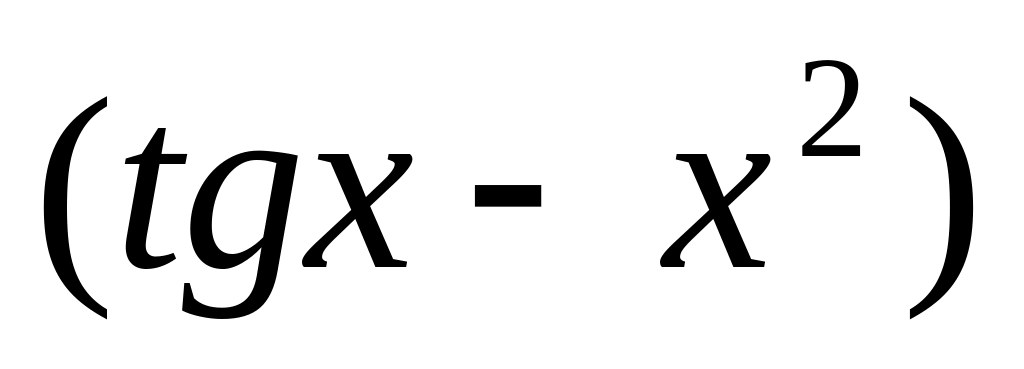 6.
y
=
6.
y
=
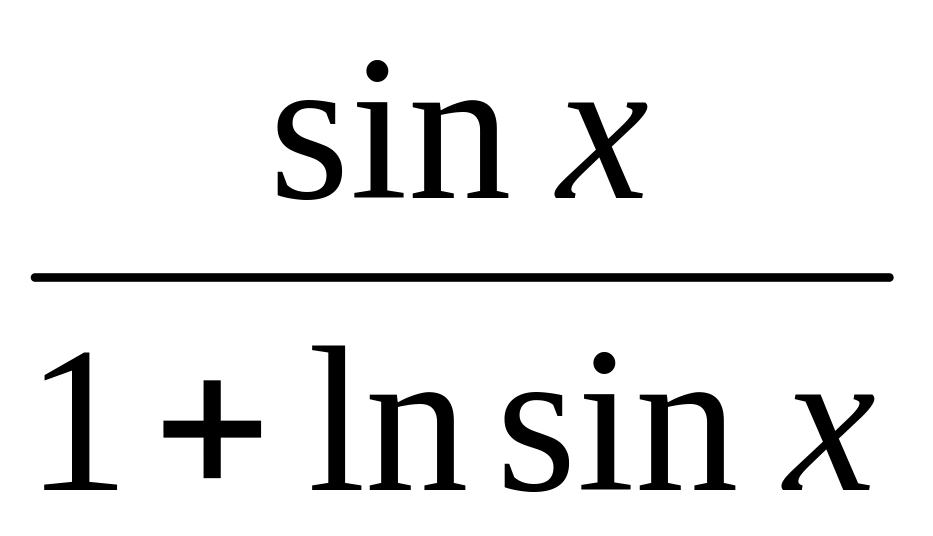
y =
 7.
y
=
7.
y
=
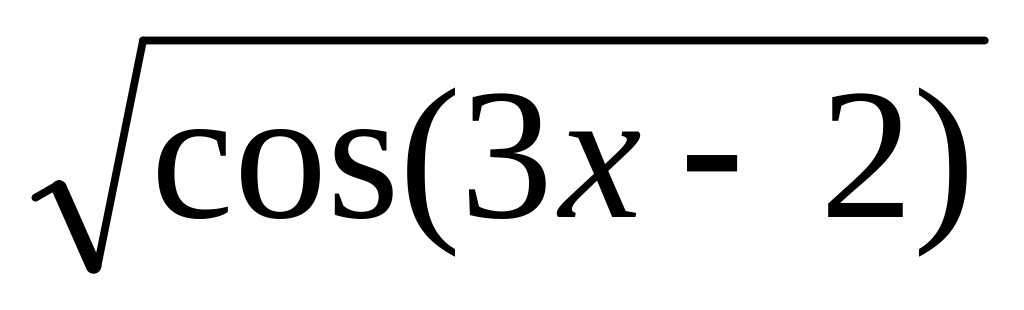
y =
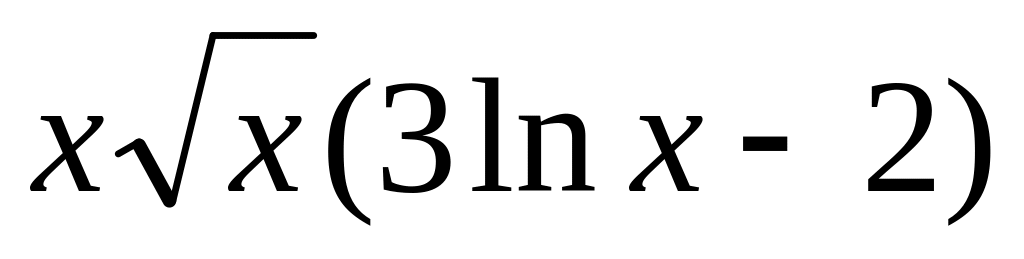 8.
S(t)
=
8.
S(t)
=
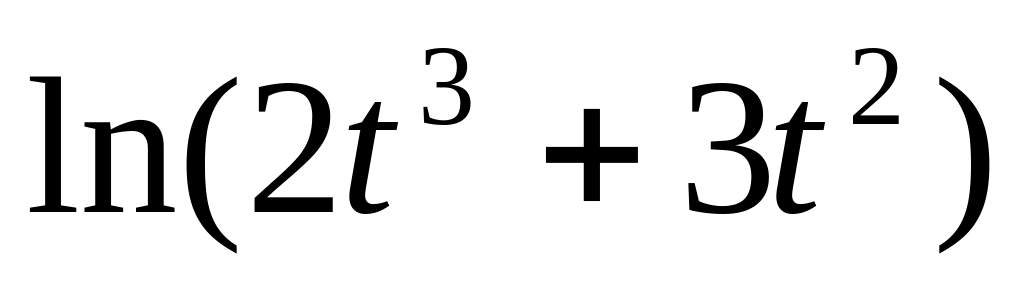
y =
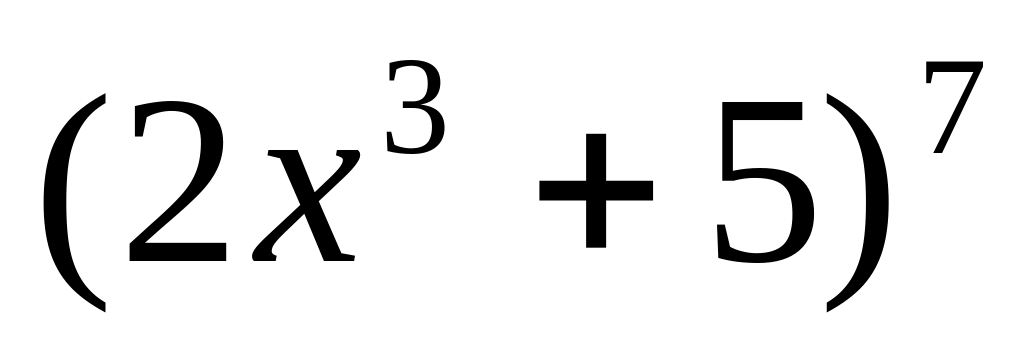 9.
y
=
9.
y
=
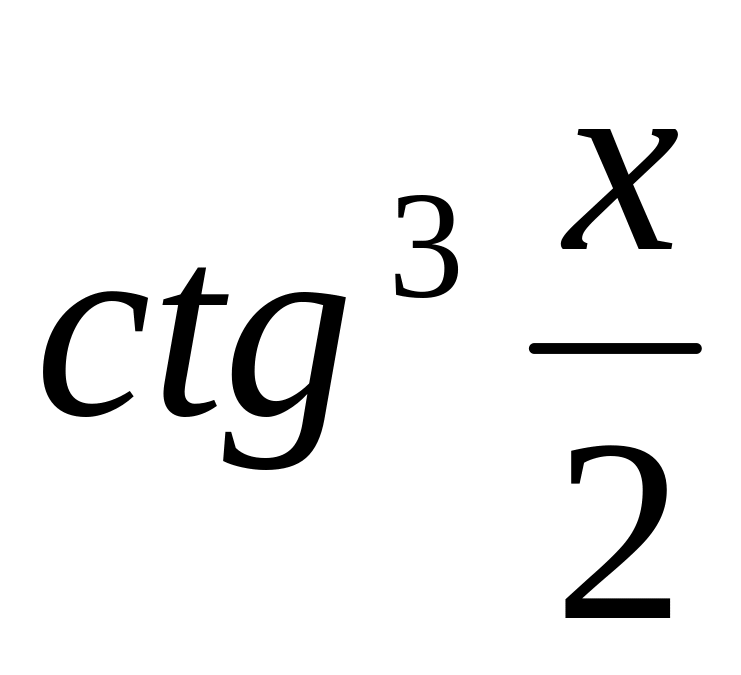
y =
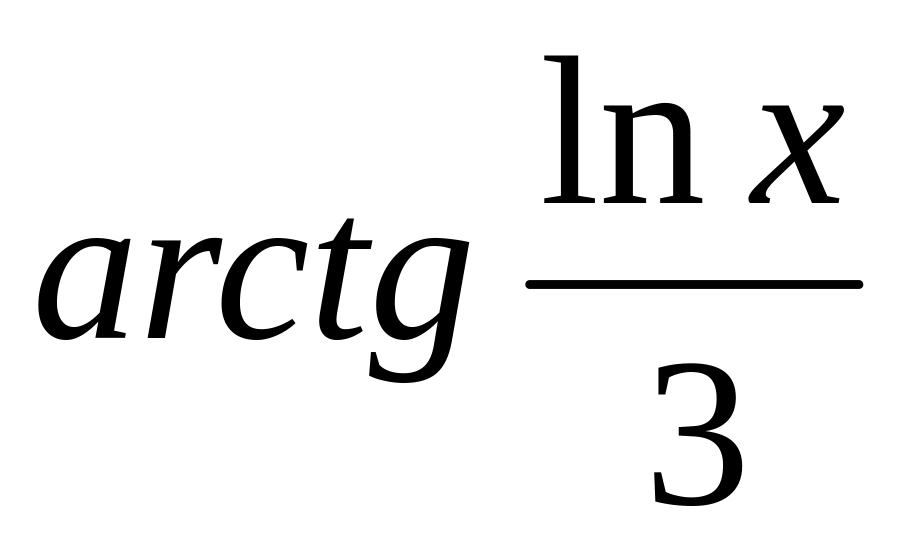 10.
y
=
10.
y
=
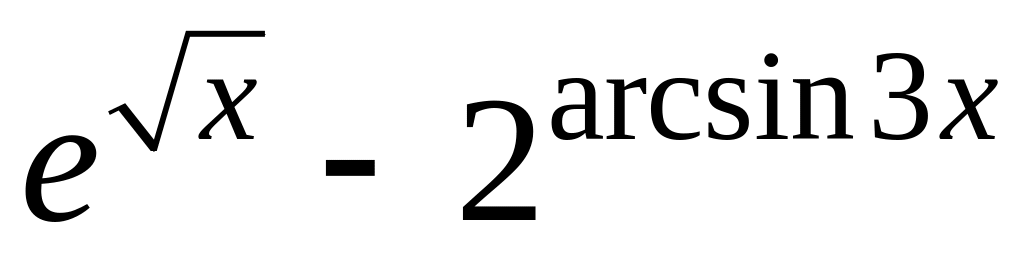
Варіант № 7
1.
![]() 6.
y
=
6.
y
=
![]()
2. y
=
![]() 7.
y
=
7.
y
=
![]()
3. z
=
![]() 8.
y
=
8.
y
=
![]()
4. S(t)
=
![]() 9.
y
=
9.
y
=
![]()
5. y
=
![]() 10.
y
=
10.
y
=
![]()
Варіант № 8
S(t) =
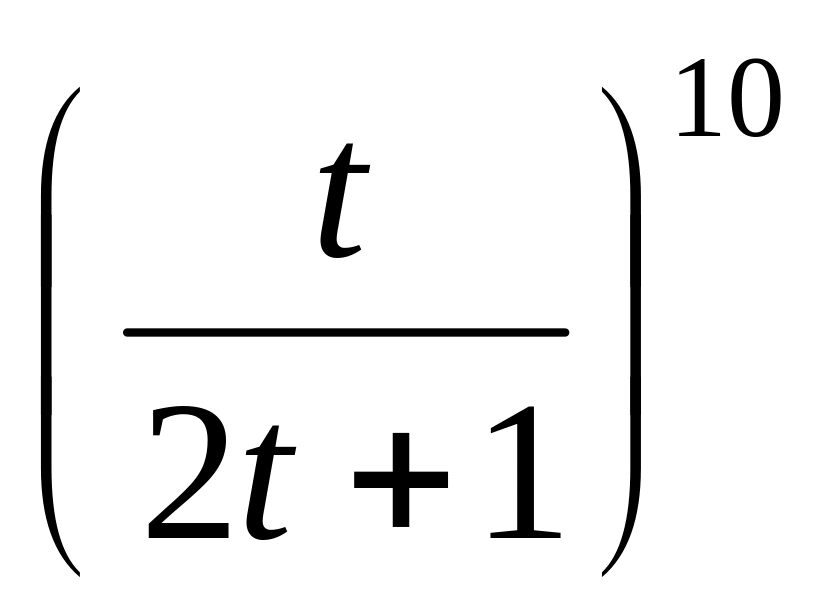
 6.
y
=
6.
y
=
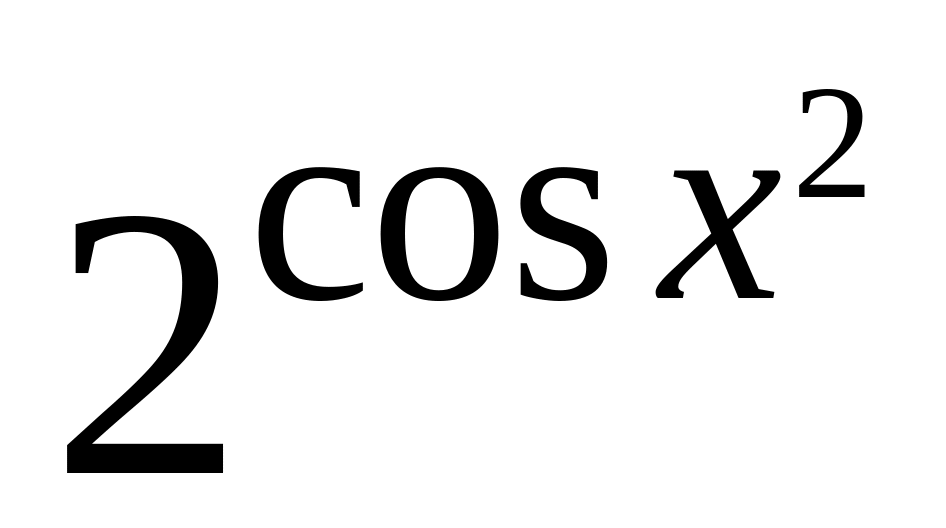
y =
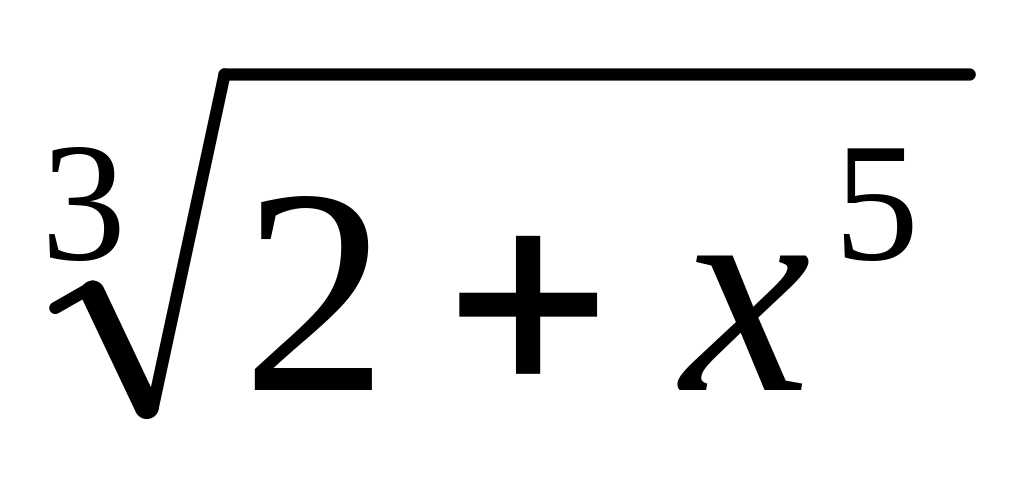 7.
y
=
7.
y
=
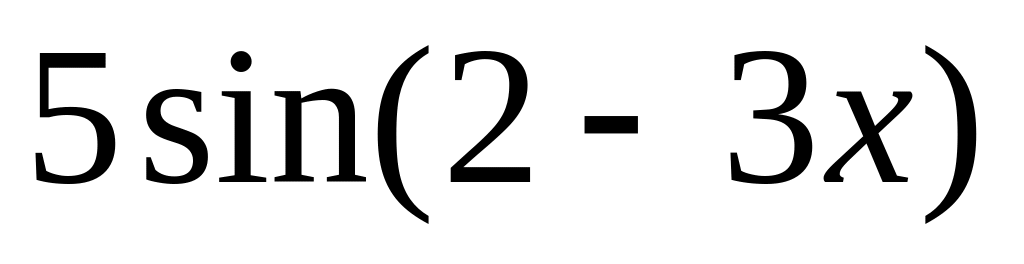
y =
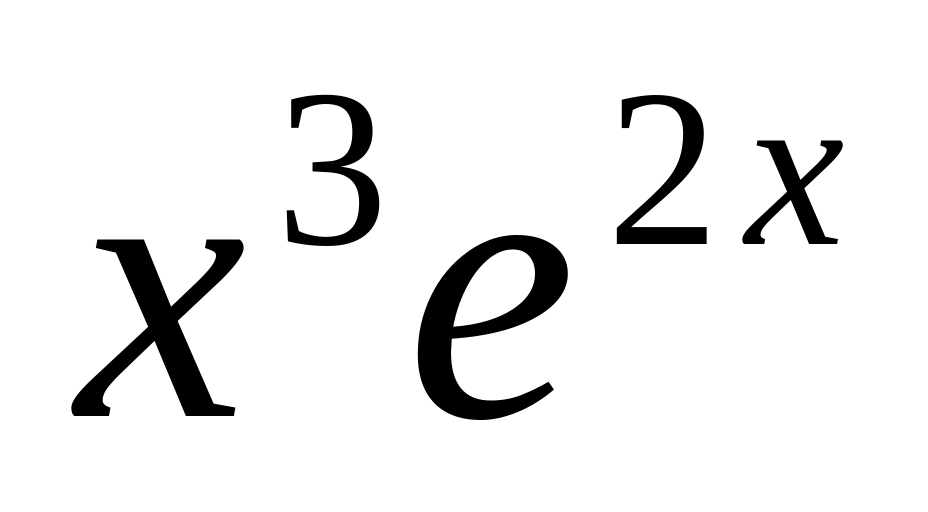 8.
y
=
8.
y
=

y =
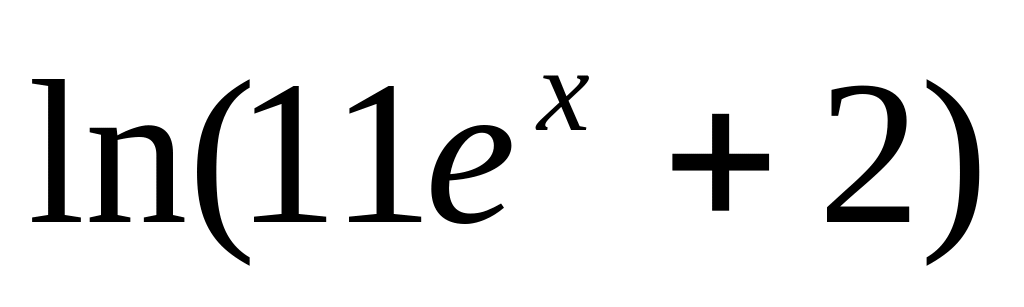 9.
z(
9.
z( )
=
)
=
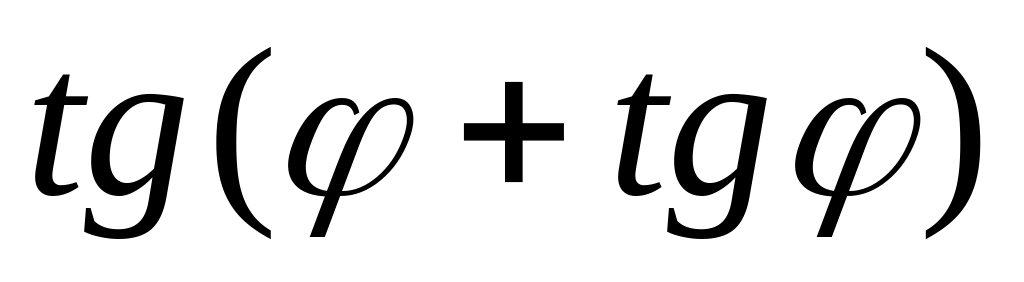
y =
 10.
y
=
10.
y
=
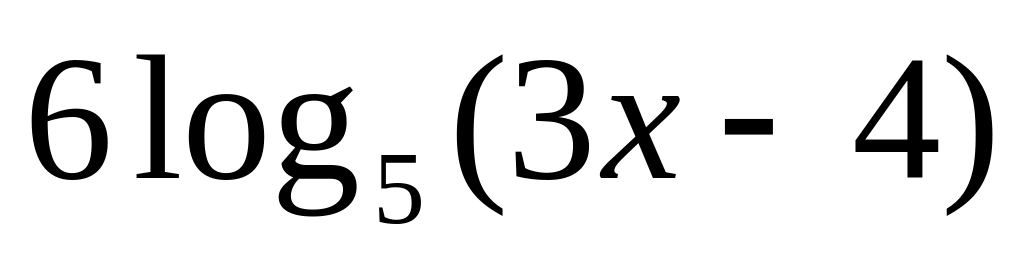
Варіант № 9
z( ) =
 6.
y
=
6.
y
=
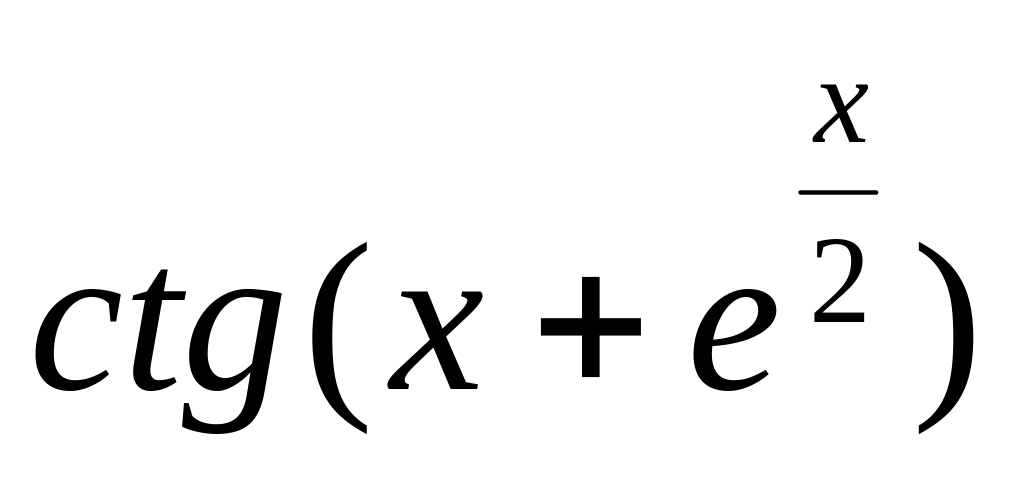
y =
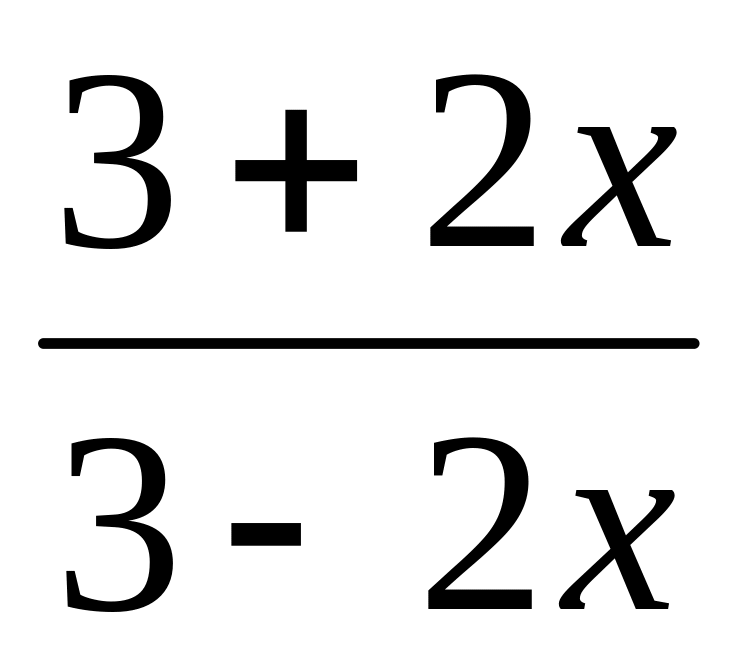 7.
y
=
7.
y
=
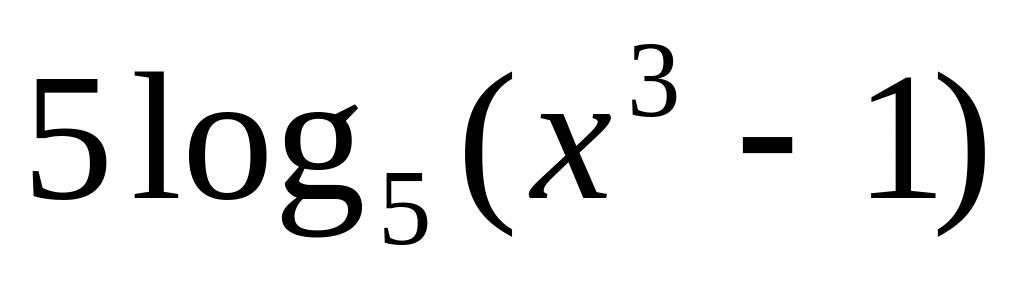
y =
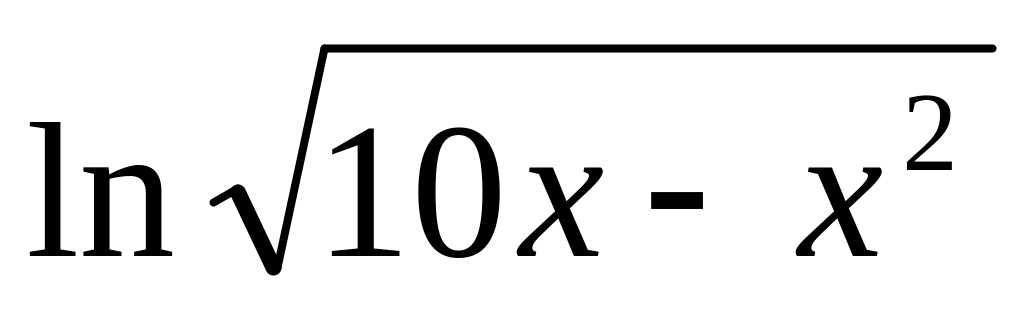 8.
y
=
8.
y
=
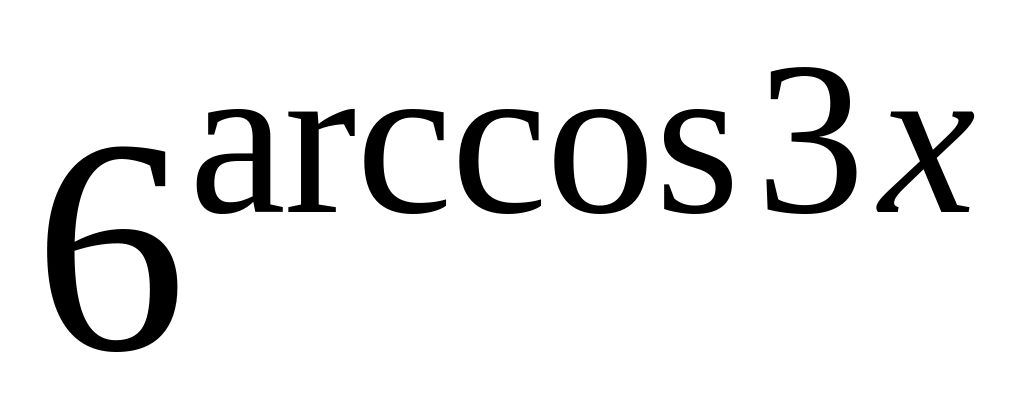
y =
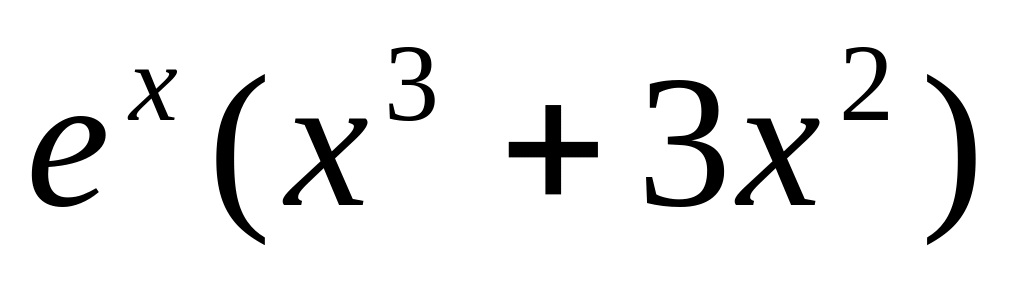 9.
y
=
9.
y
=

y =
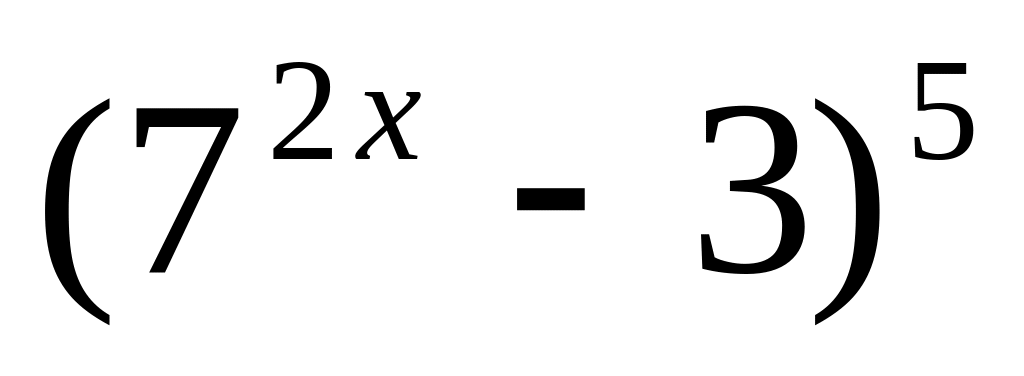 10.
y
=
10.
y
=
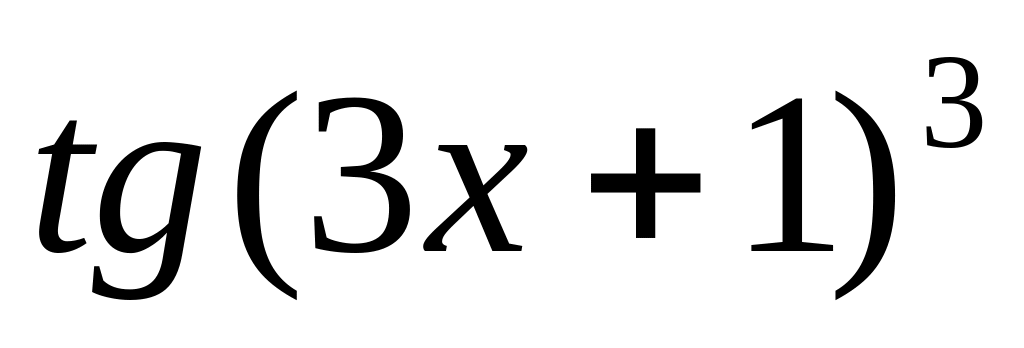
Варіант № 10
y =
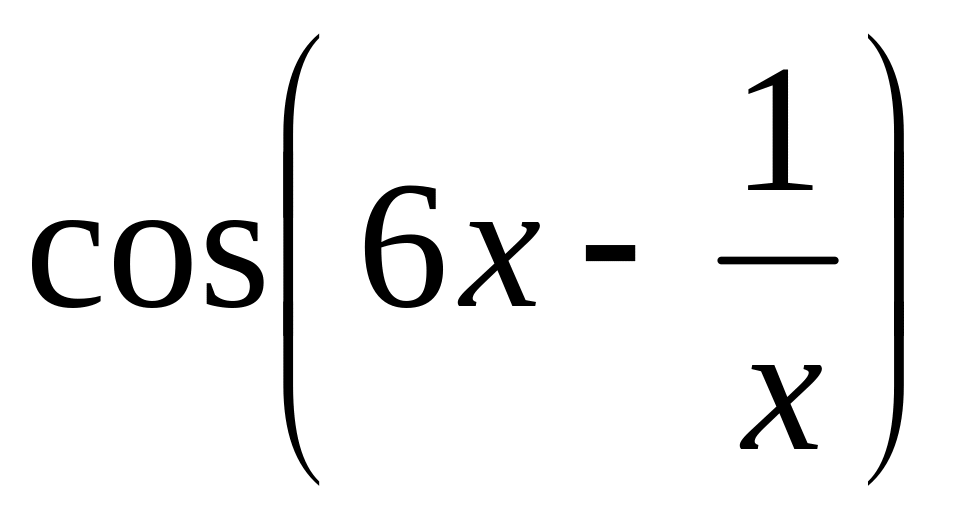 6.
y
=
6.
y
=
y =
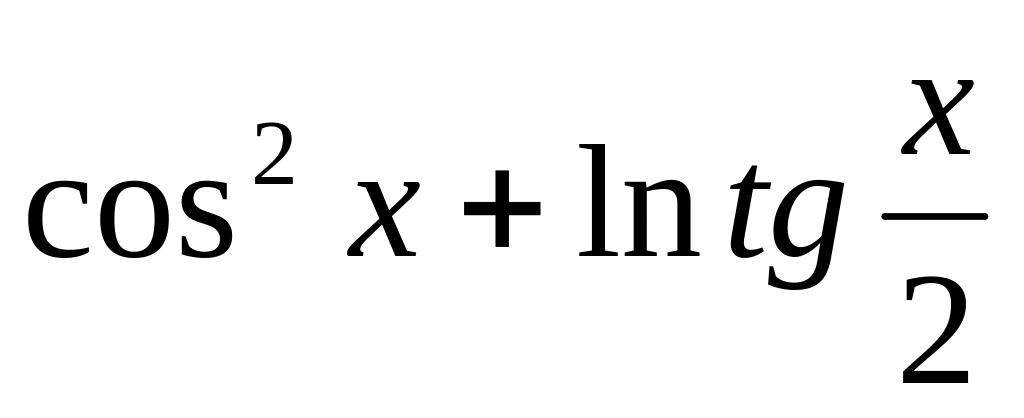 7.
y
=
7.
y
=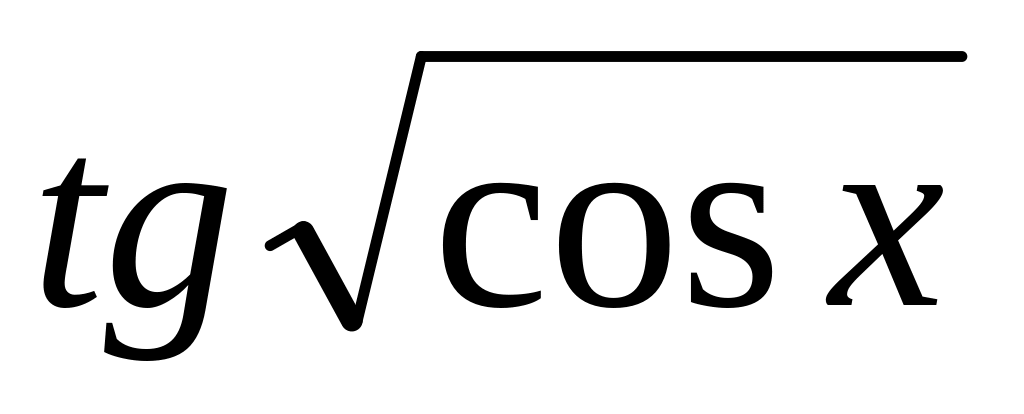
y =
 8.
y
=
8.
y
=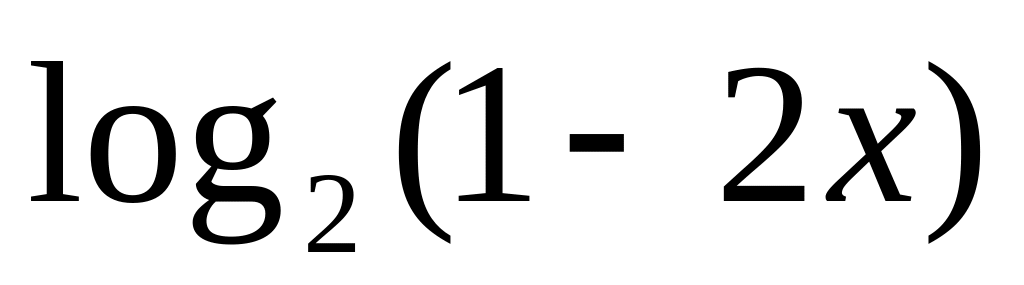
y =
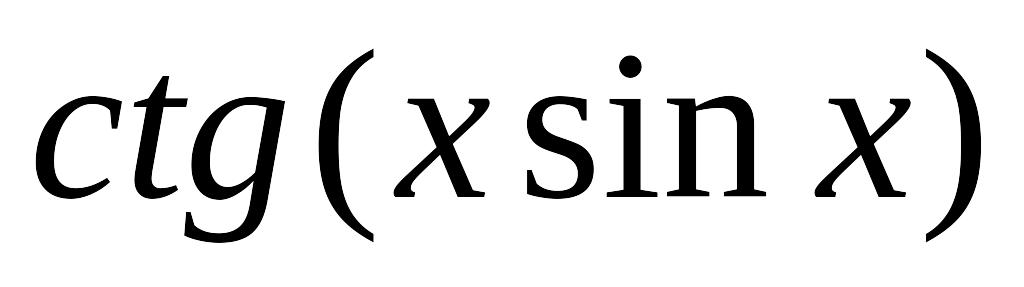 9.
y
=
9.
y
=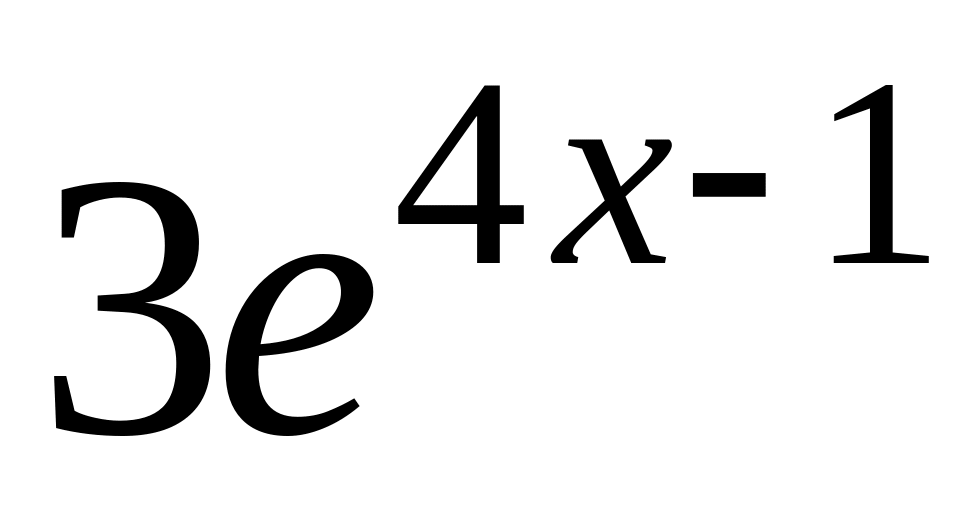
z(t) =
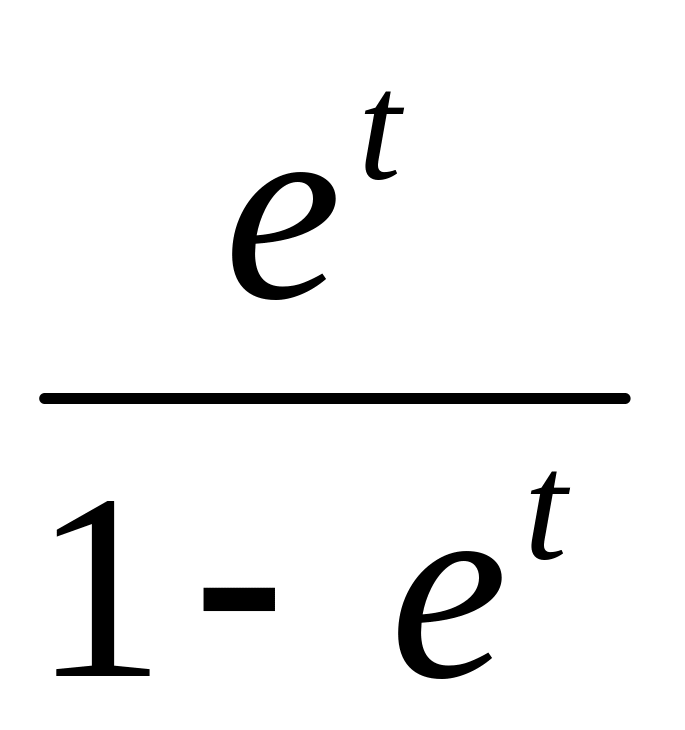 10.
y
=
10.
y
=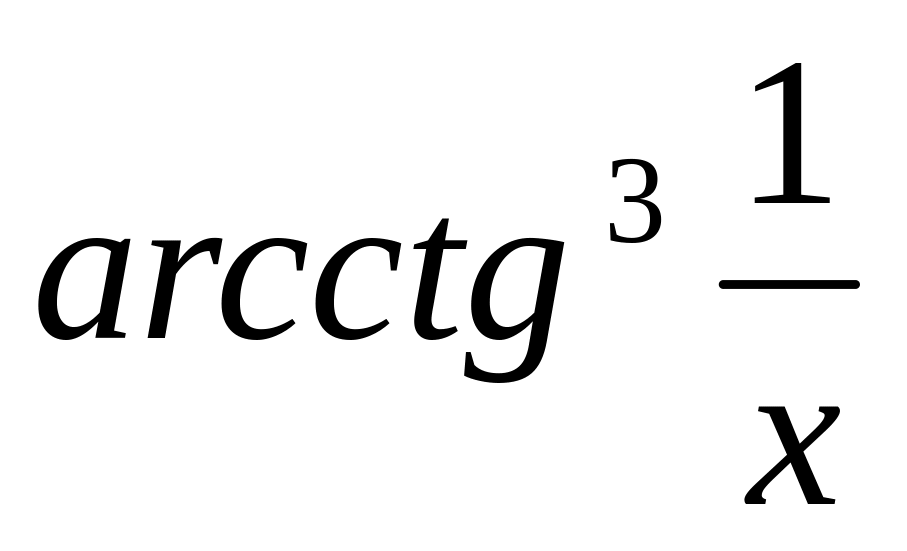
Варіант № 11
y =
 6.
y
=
6.
y
=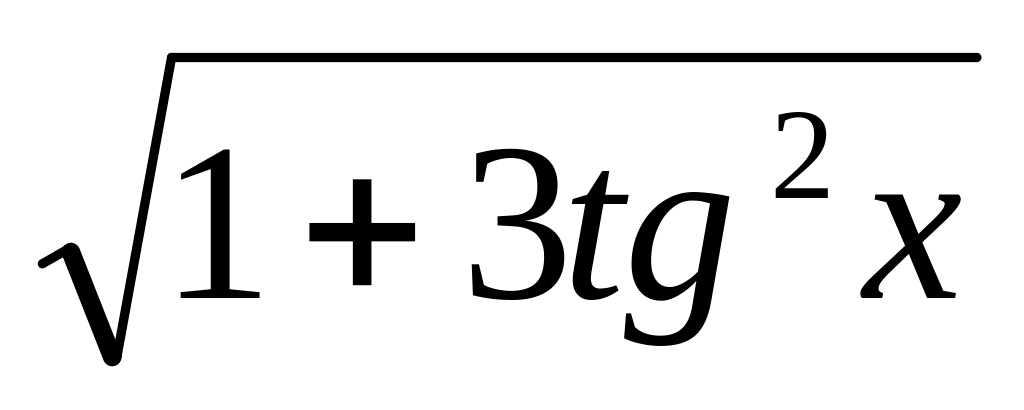
y =
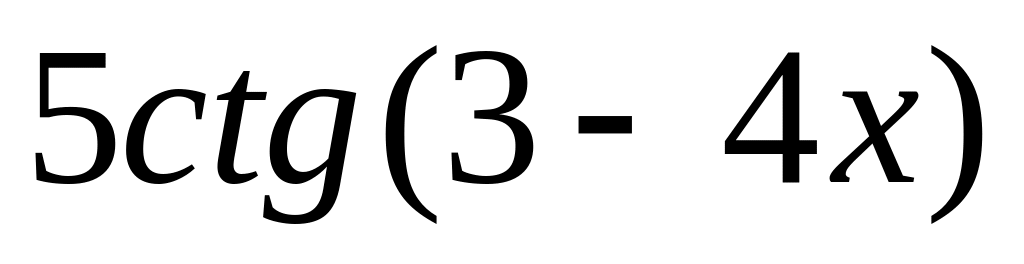 7.
y
=
7.
y
=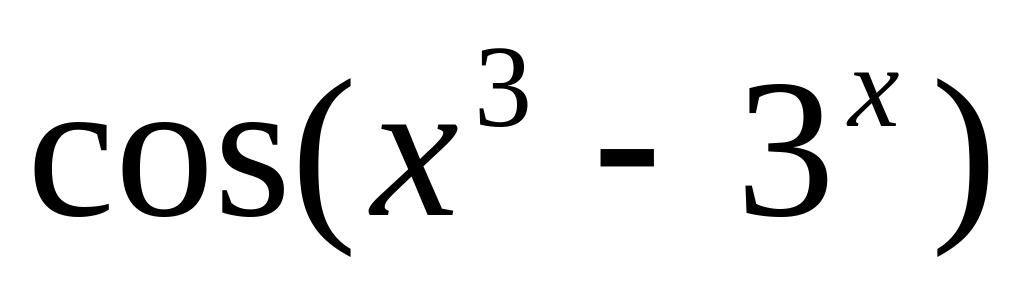
y =
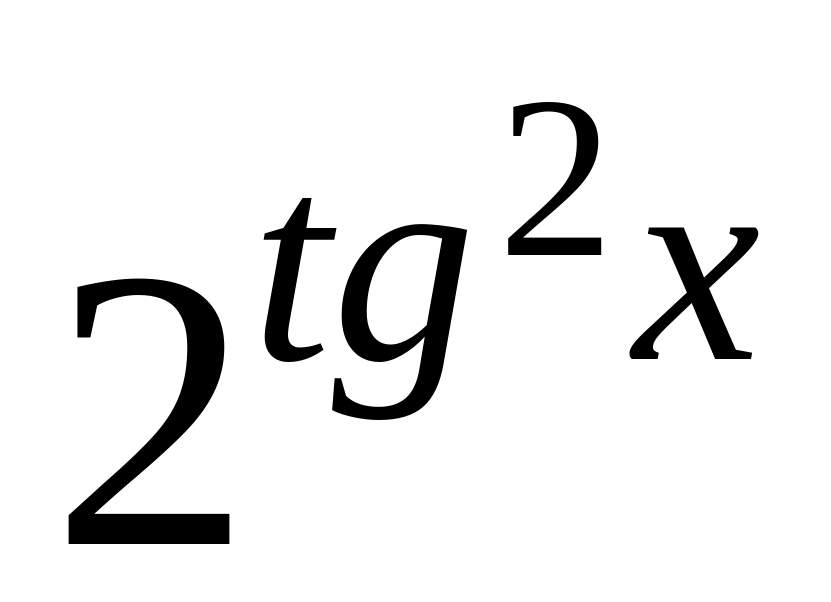 8.
y
=
8.
y
=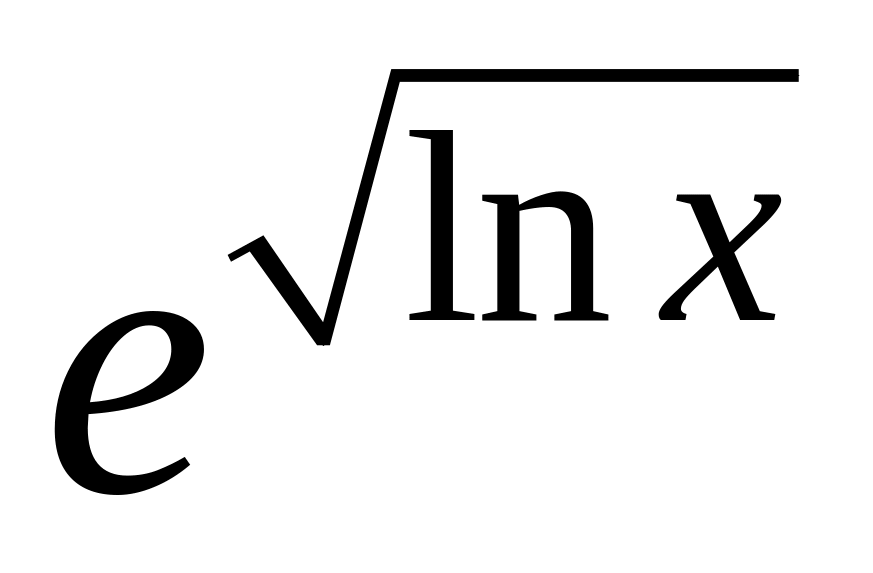
y =
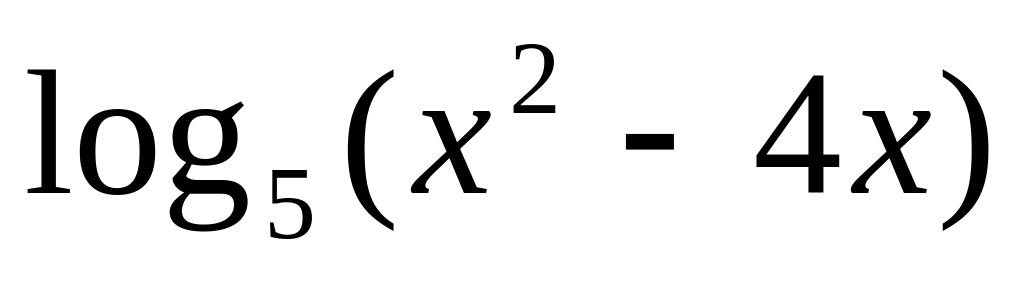 9.
y
=
9.
y
=
y =
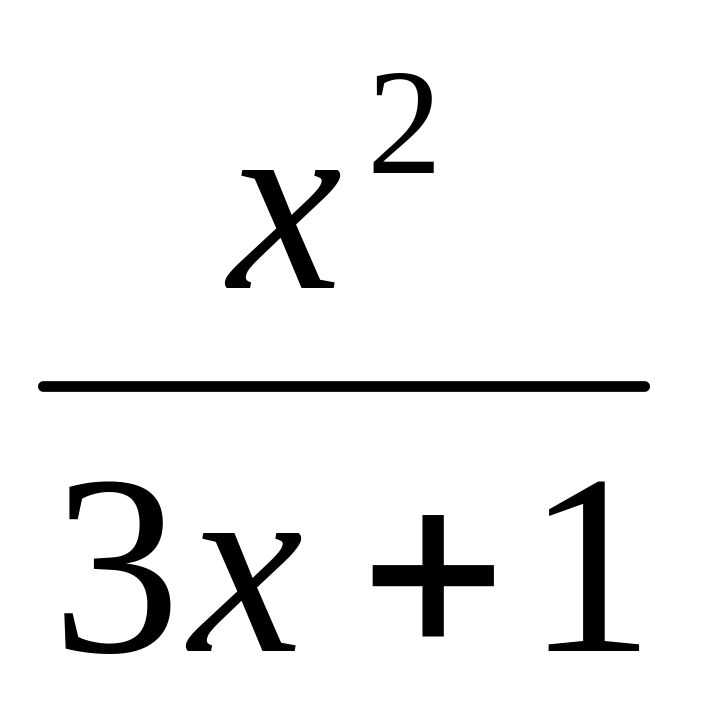 10.
y
=
10.
y
=
Варіант № 12
y =
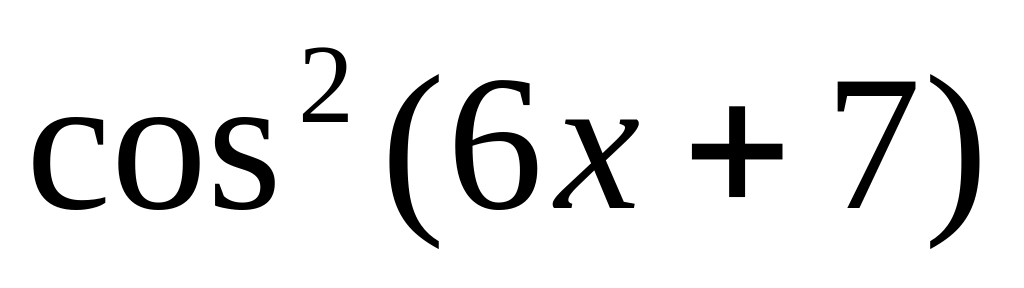 6.
y
=
6.
y
=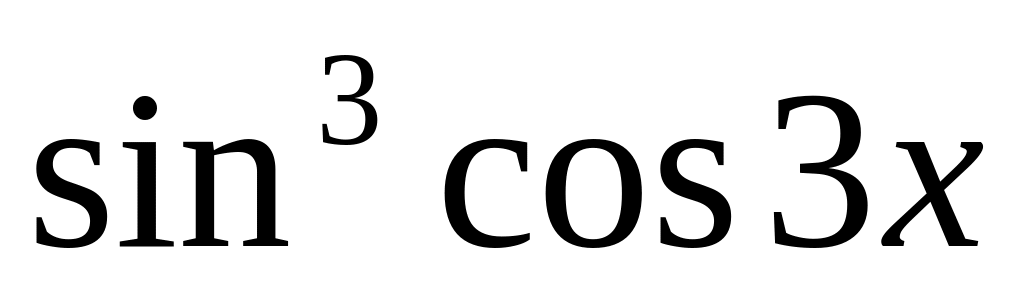
y =
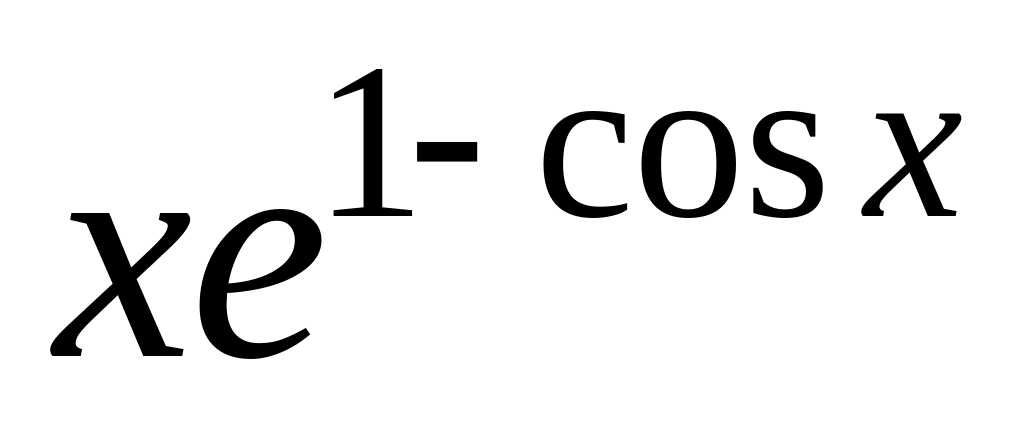 7.
y
=
7.
y
=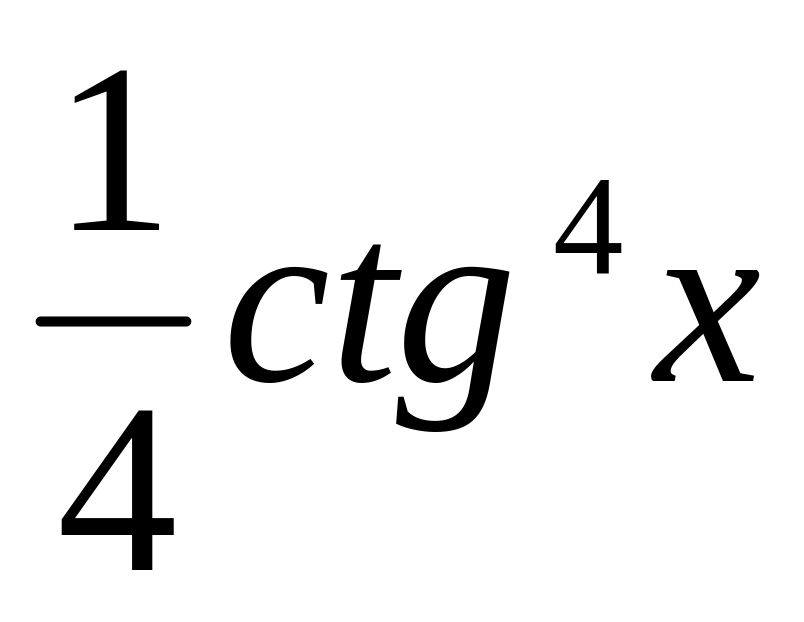
y =
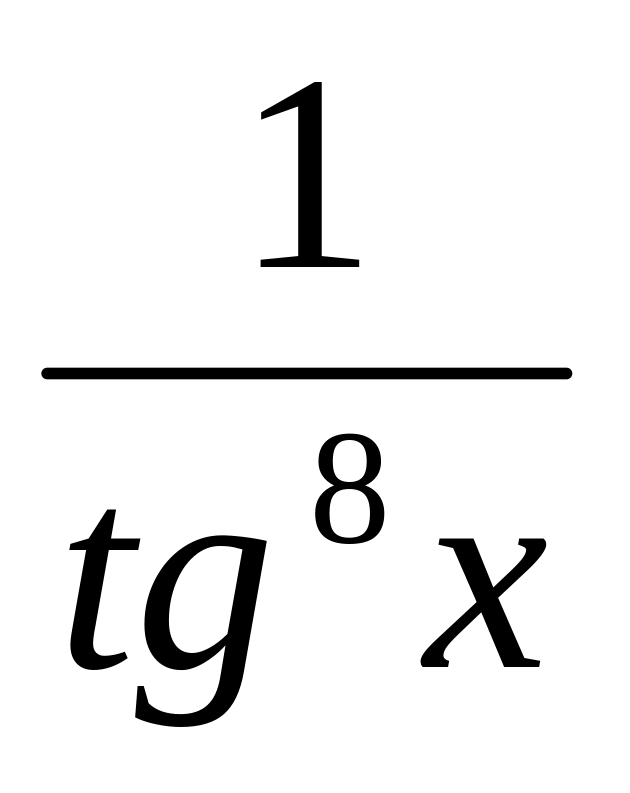 8.
y
=
8.
y
=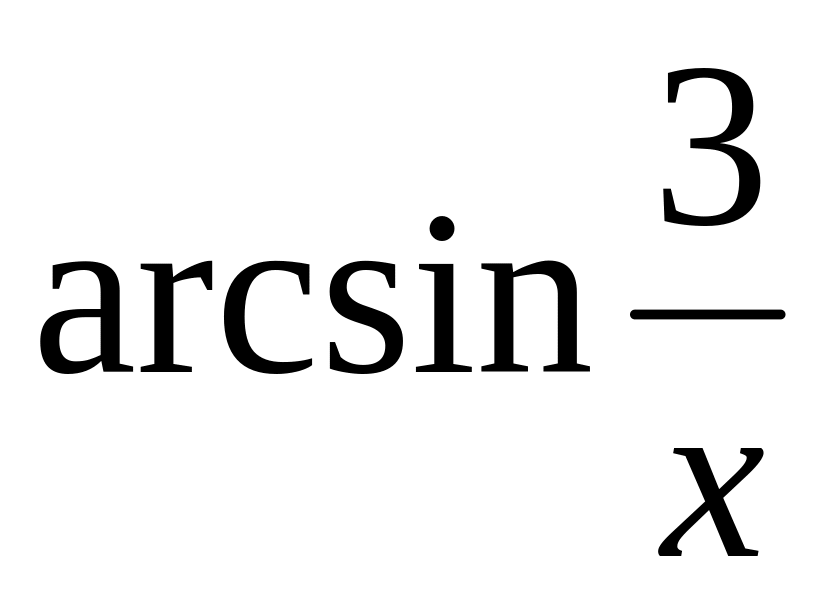
f(t) =
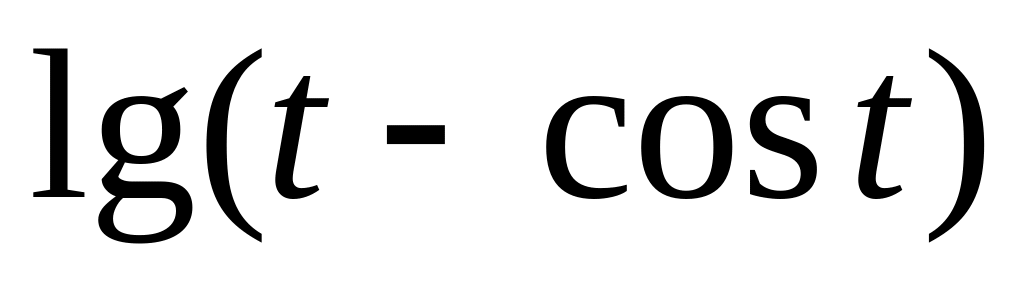 9.
y
=
9.
y
=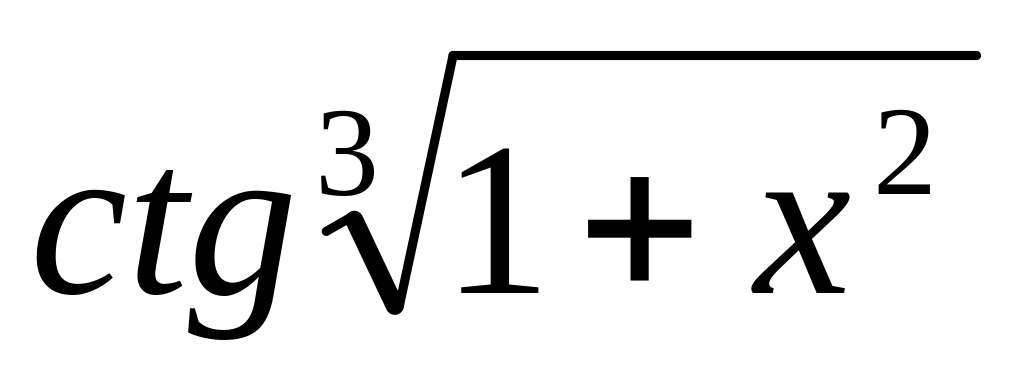
r( ) =
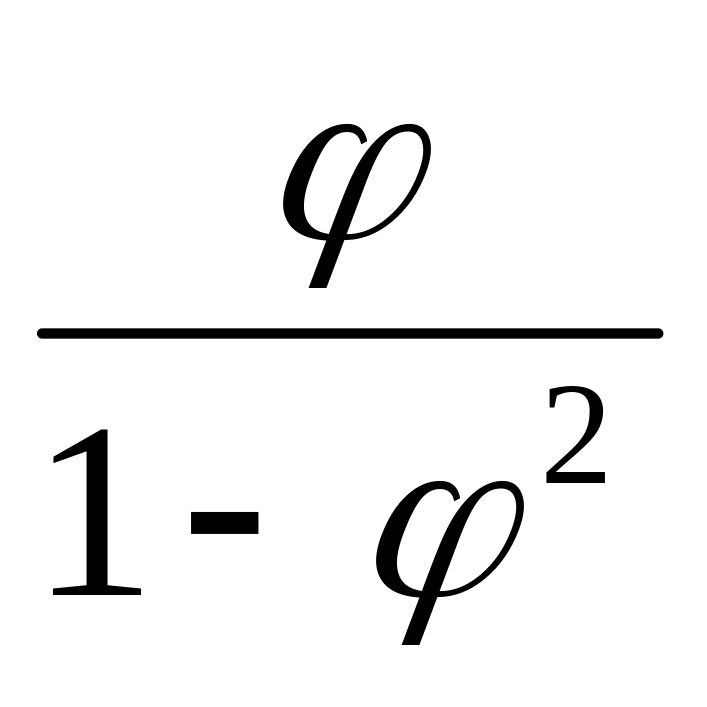 10.
y
=
10.
y
=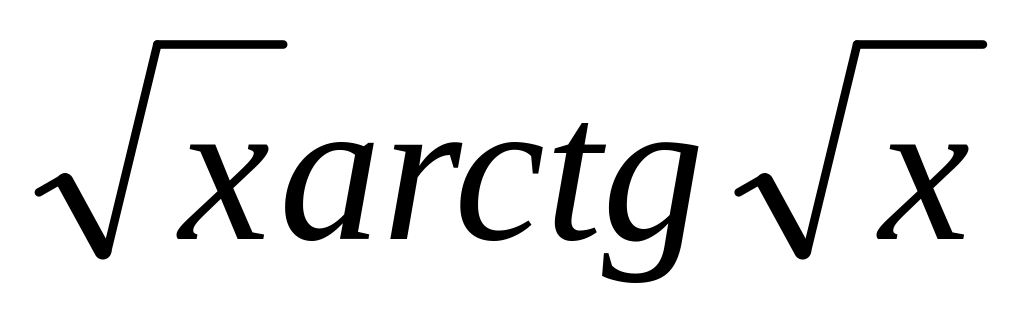
Варіант № 13
S(t) =
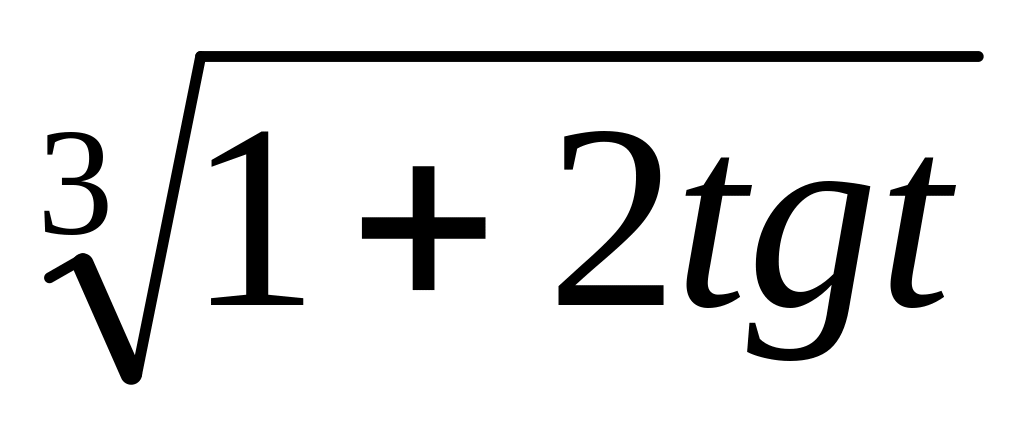 6.
y
=
6.
y
=
y =
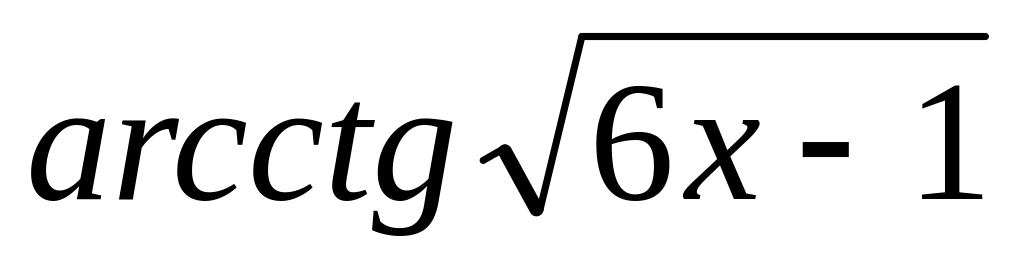 7.
y
=
7.
y
=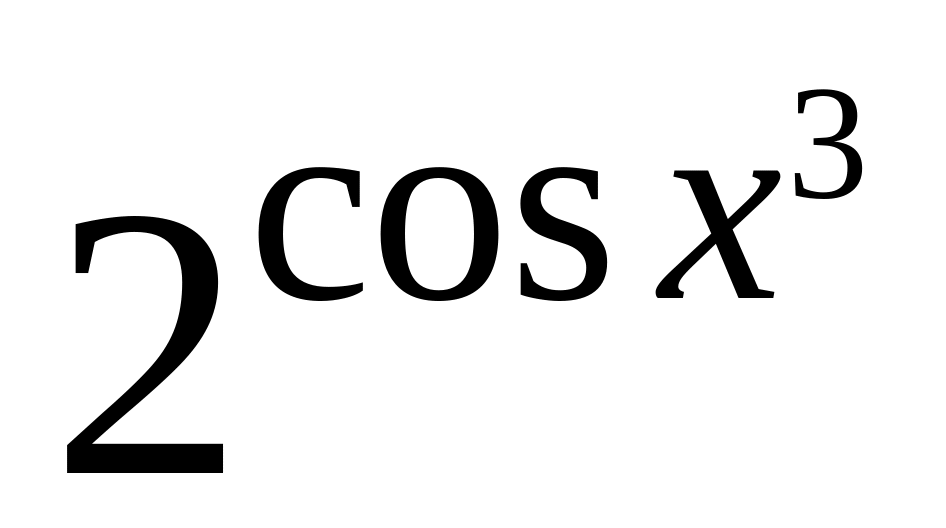
y =
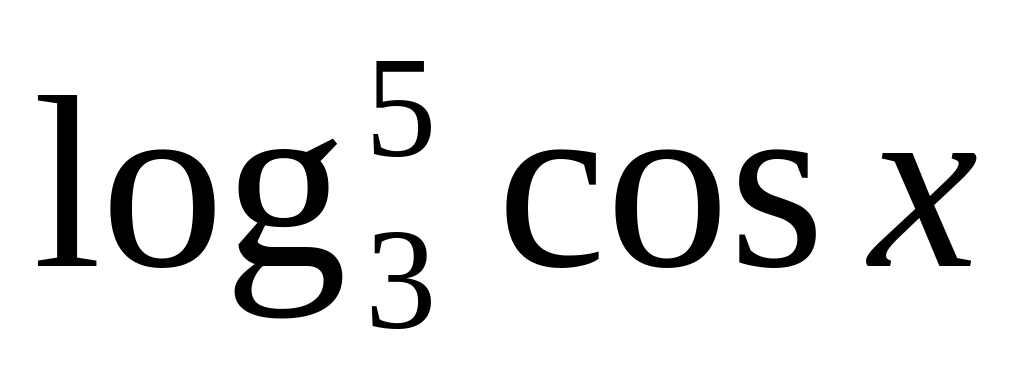 8.
y
=
8.
y
=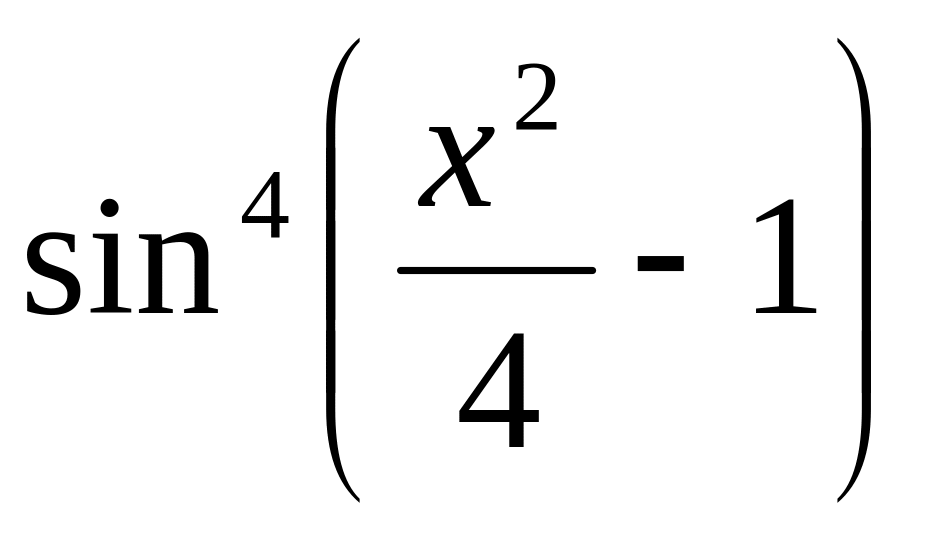
y =
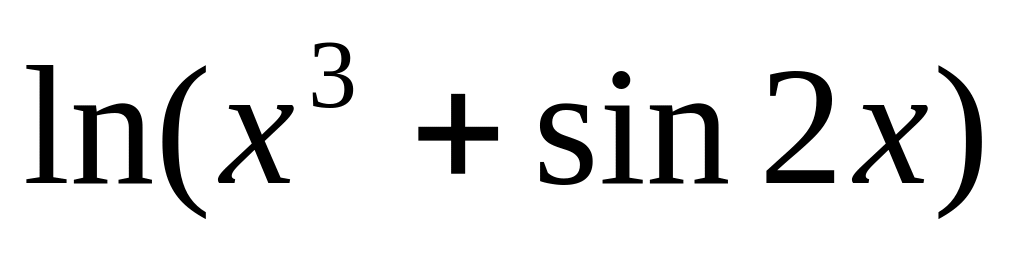 9.
y
=
9.
y
=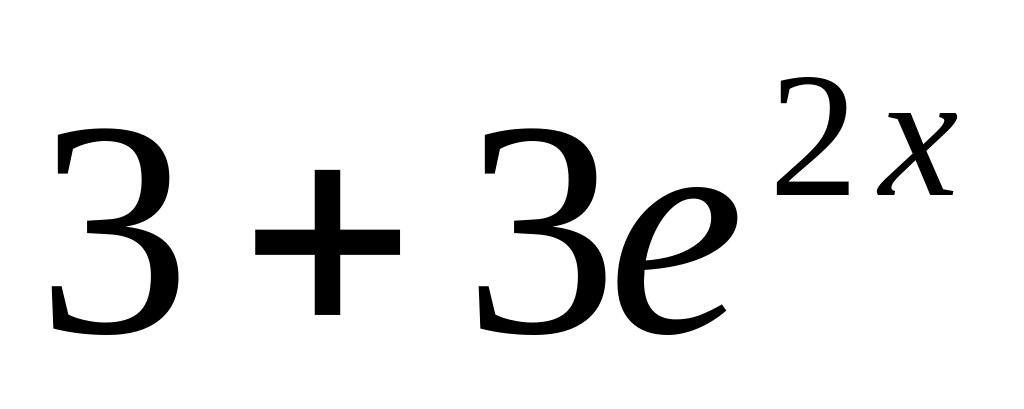
y =
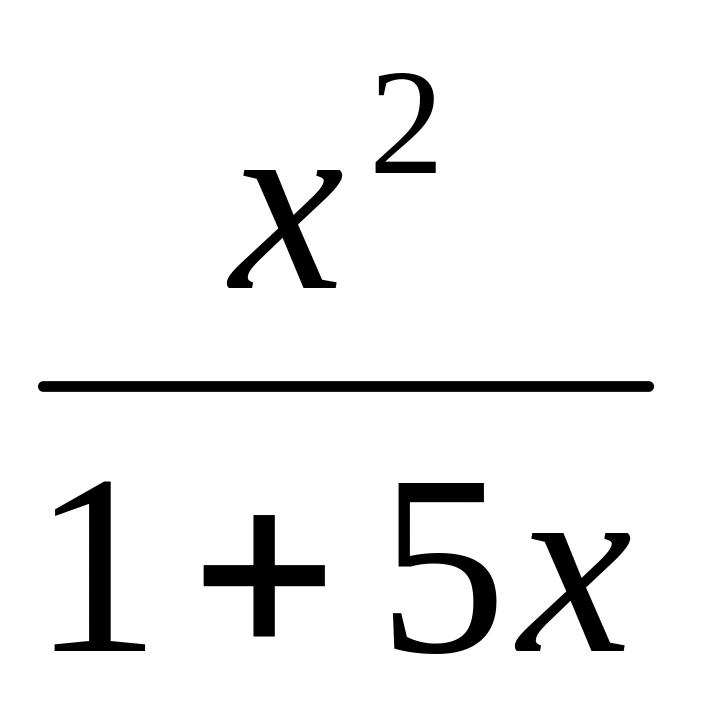 10.
y
=
10.
y
=
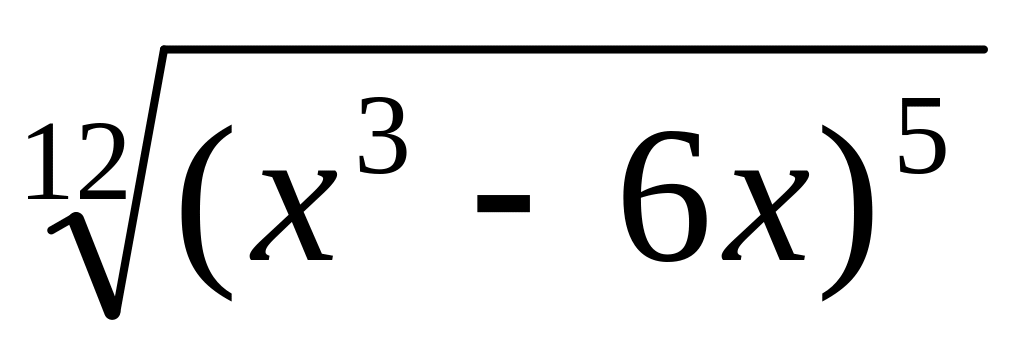
Варіант № 14
S(t) =
 6.
y
=
6.
y
=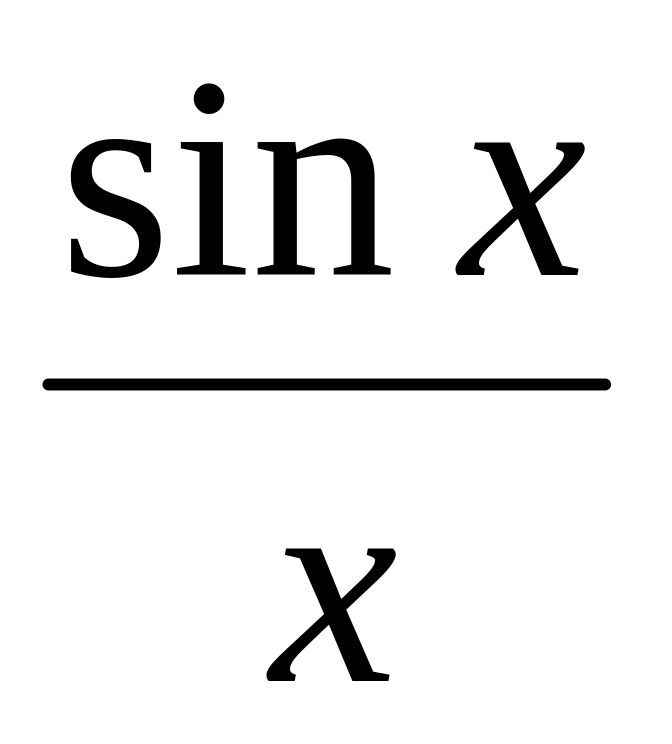
y =
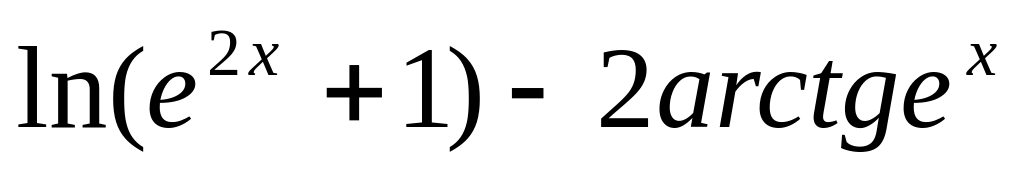 7.
y
=
7.
y
=
y =
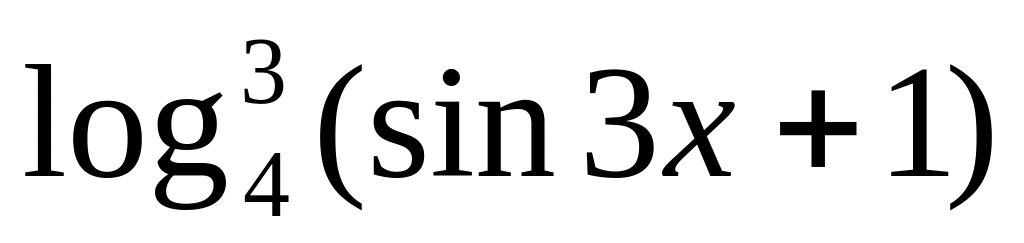 8.
r(
)
=
8.
r(
)
=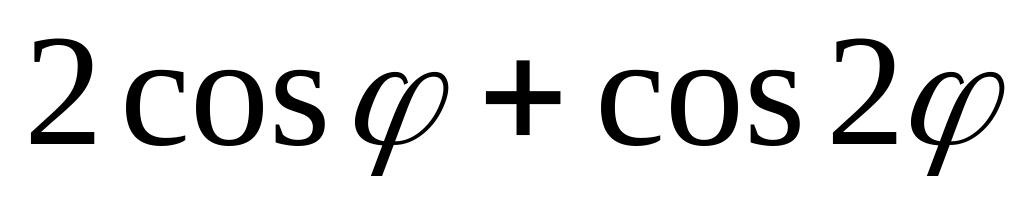
y =
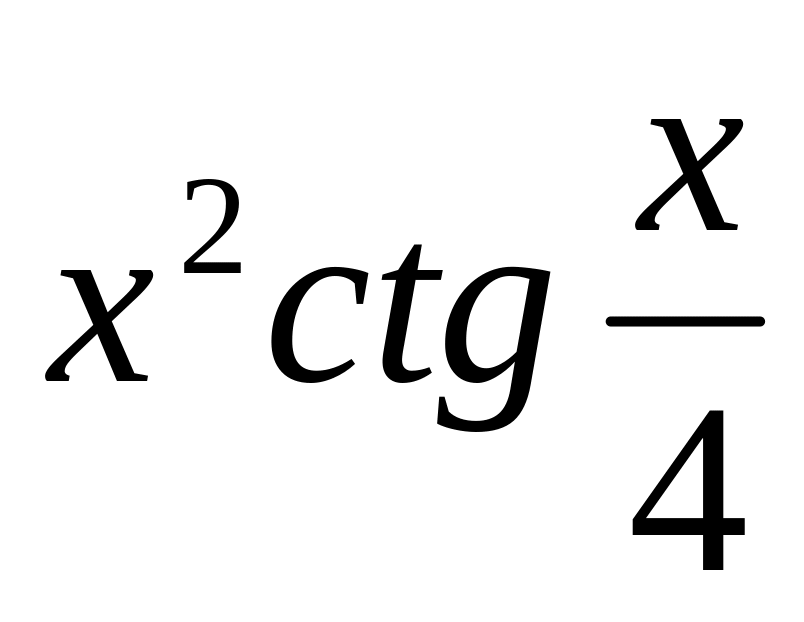 9.
y
=
9.
y
=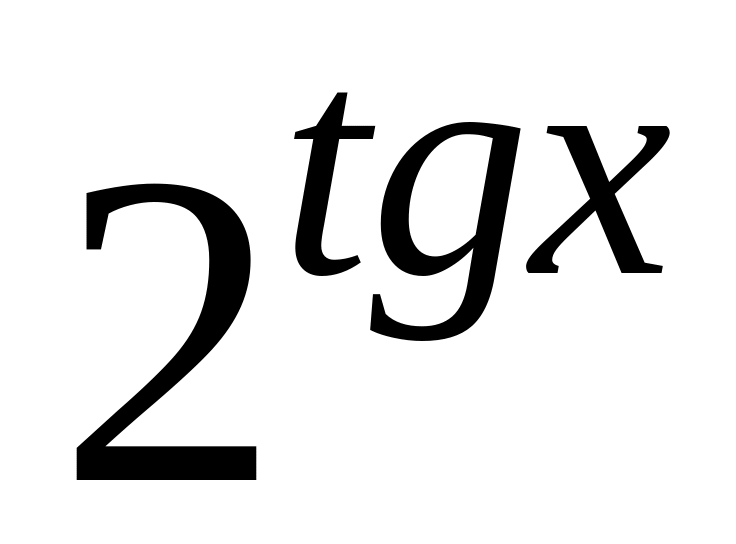
y =
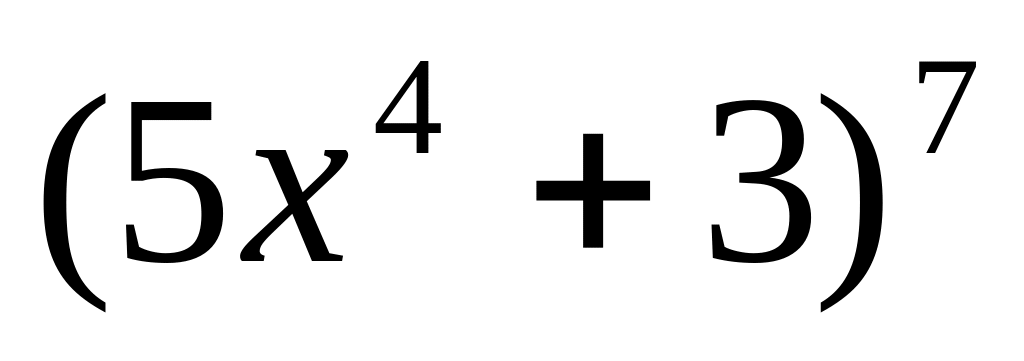 10.
y
=
10.
y
=
Варіант № 15
y =
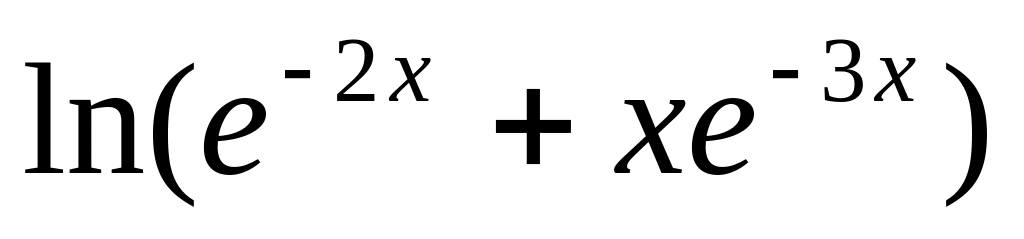 6.
S(t)
=
6.
S(t)
=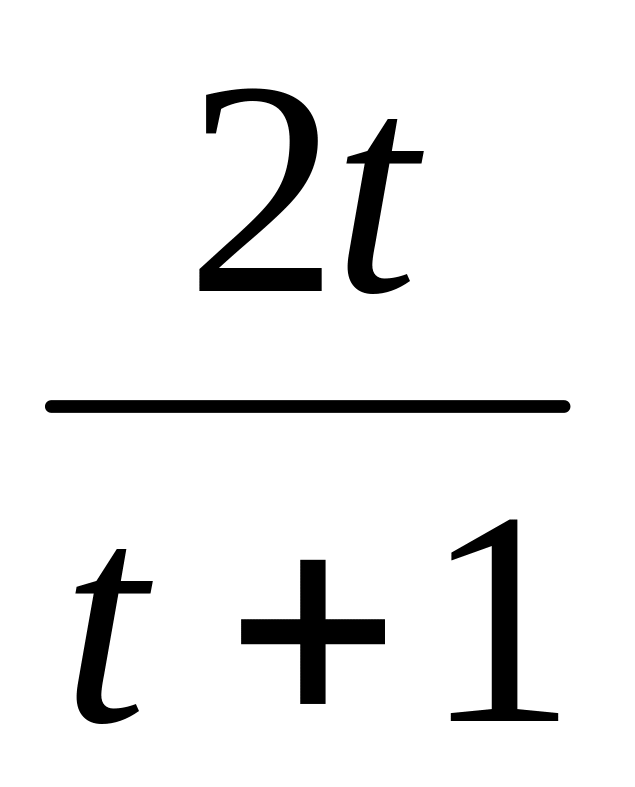
y =
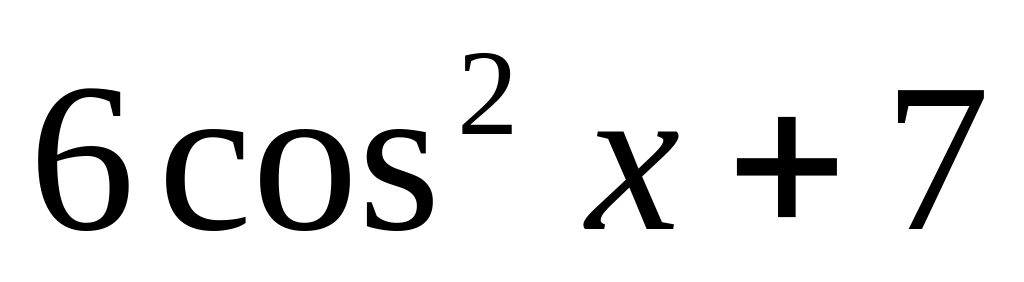 7.
y
=
7.
y
=
y =
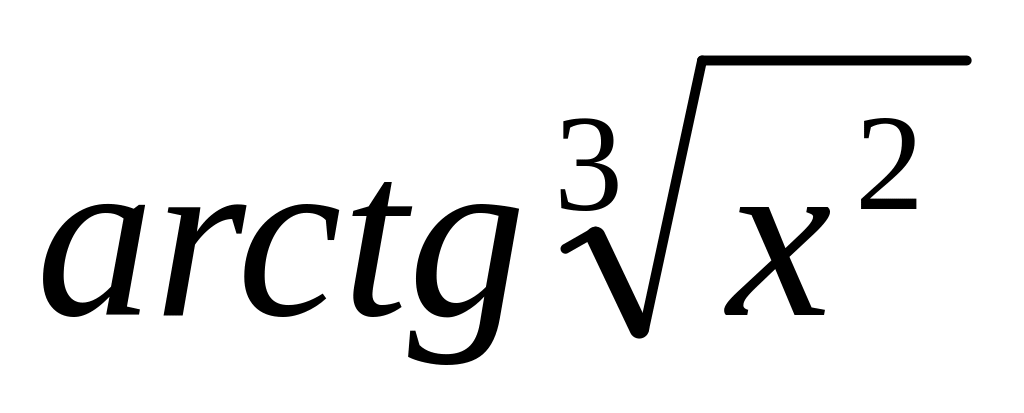 8.
y
=
8.
y
=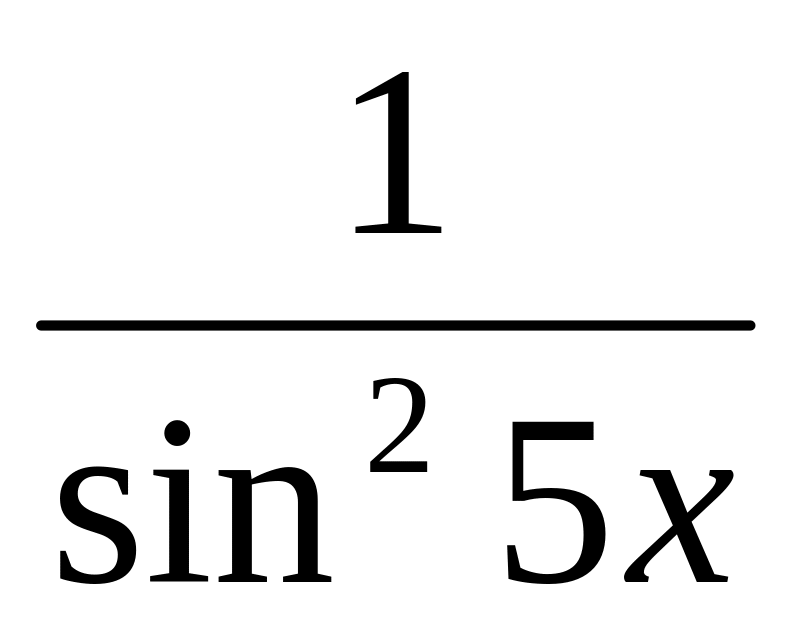
y =
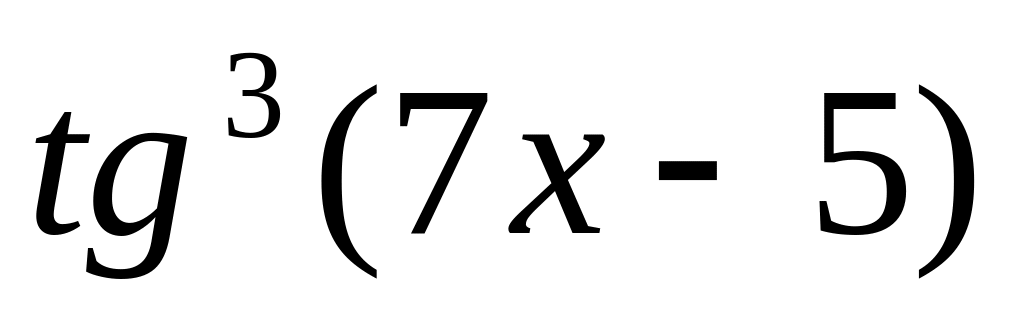 9.
y
=
9.
y
=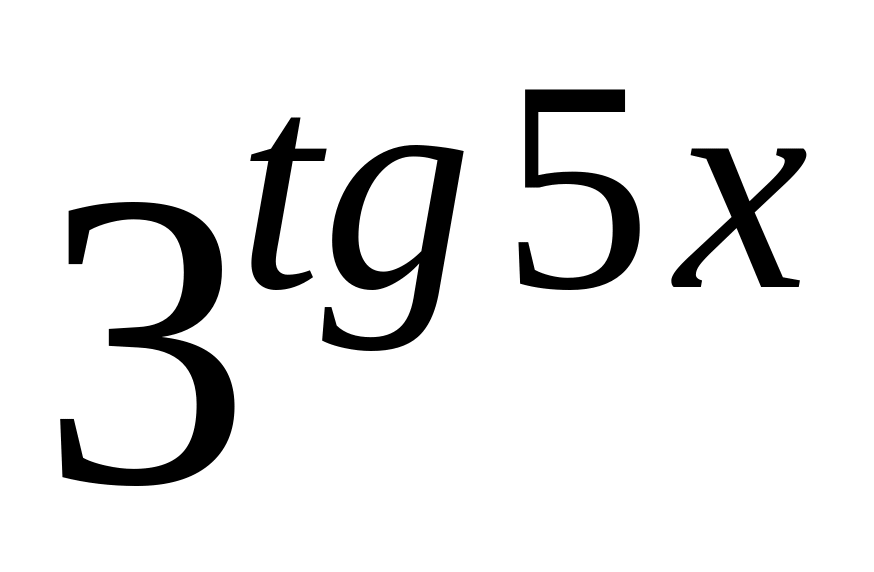
r( ) =
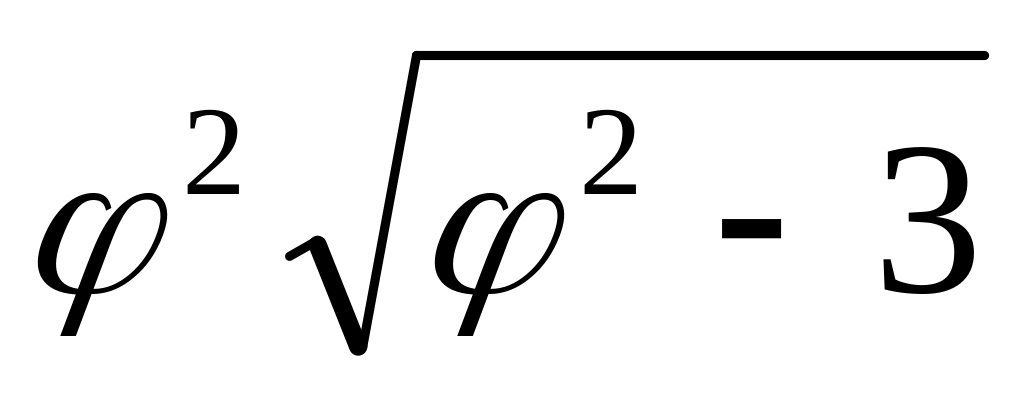 10.
y
=3
10.
y
=3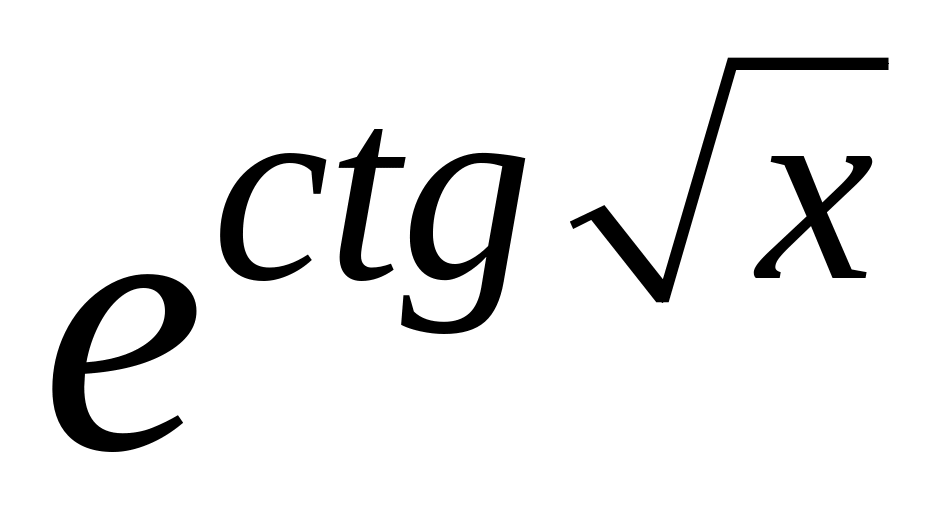
Варіант № 16
y =
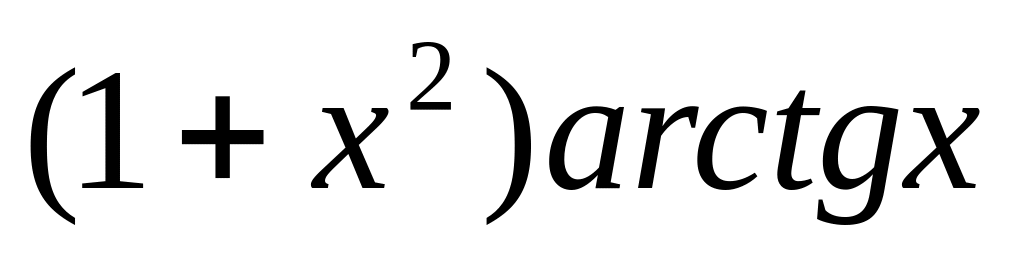 6.
y
=
6.
y
=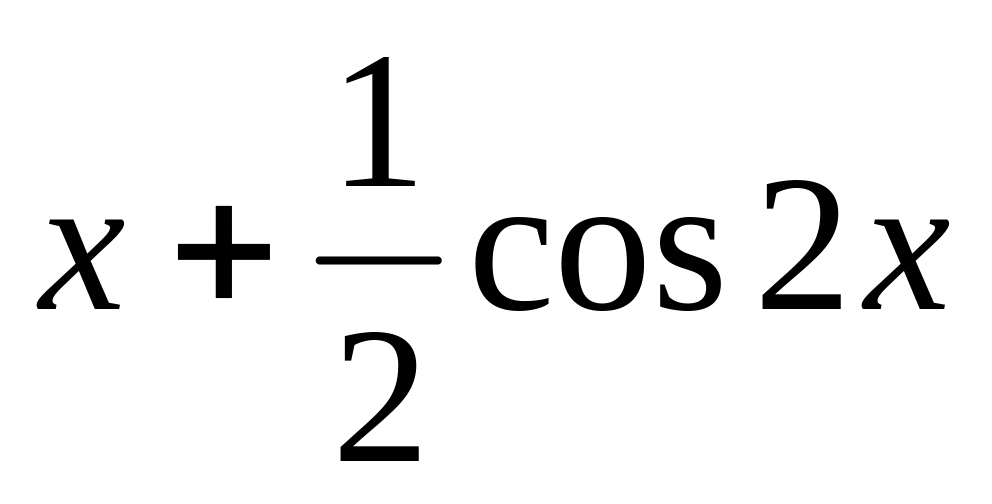
y =
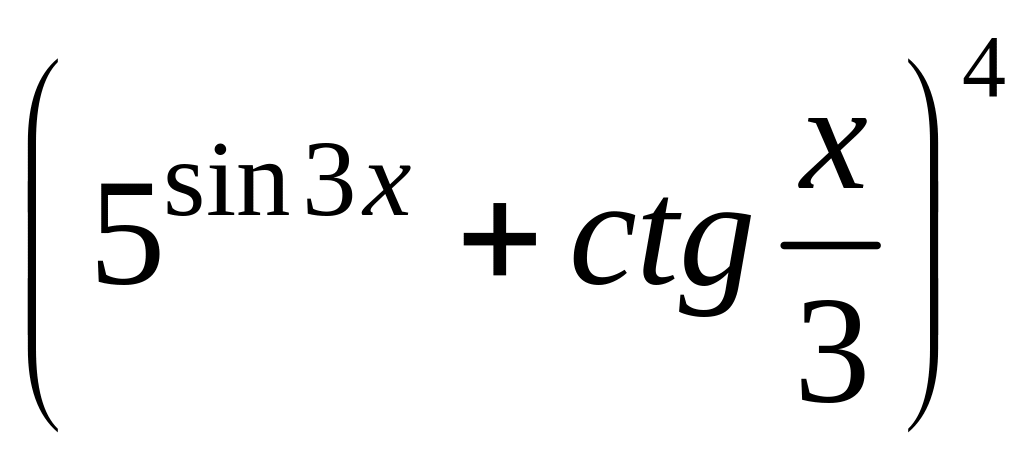 7.
y
=
7.
y
=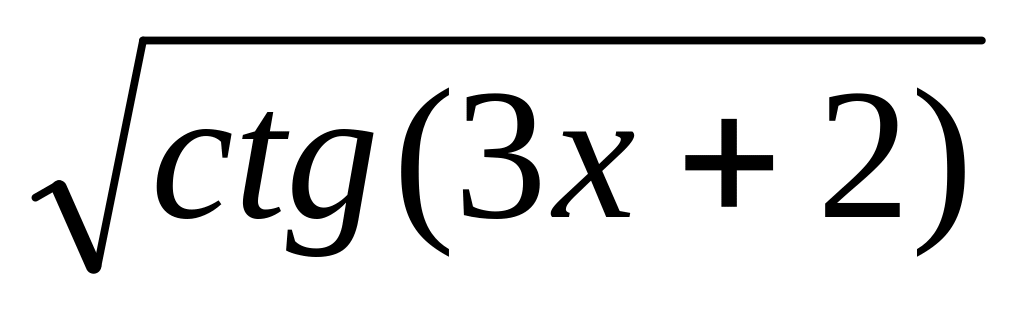
y =
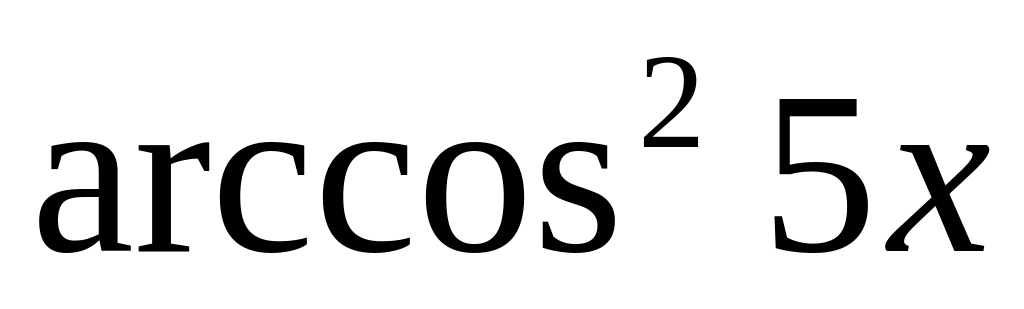 8.
y
=
8.
y
=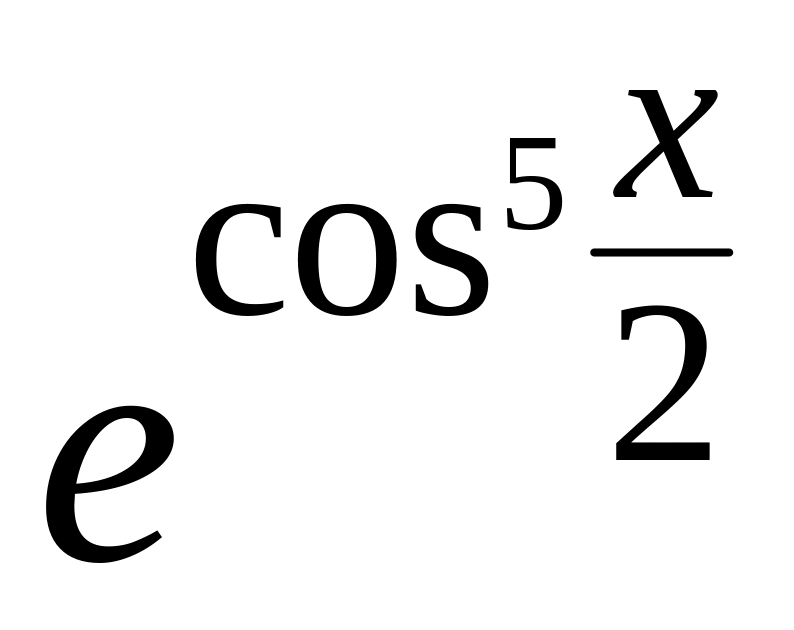
S(t) =
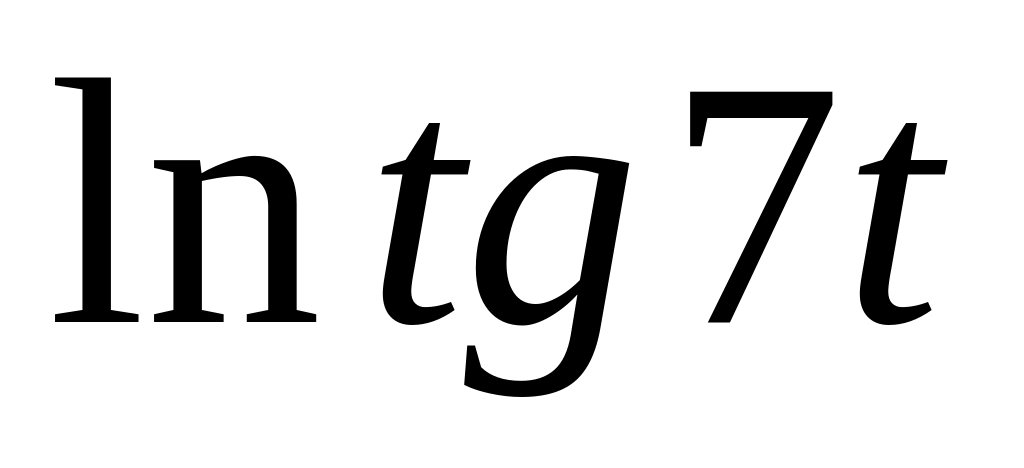 9.
f(t)
=
9.
f(t)
=
y =
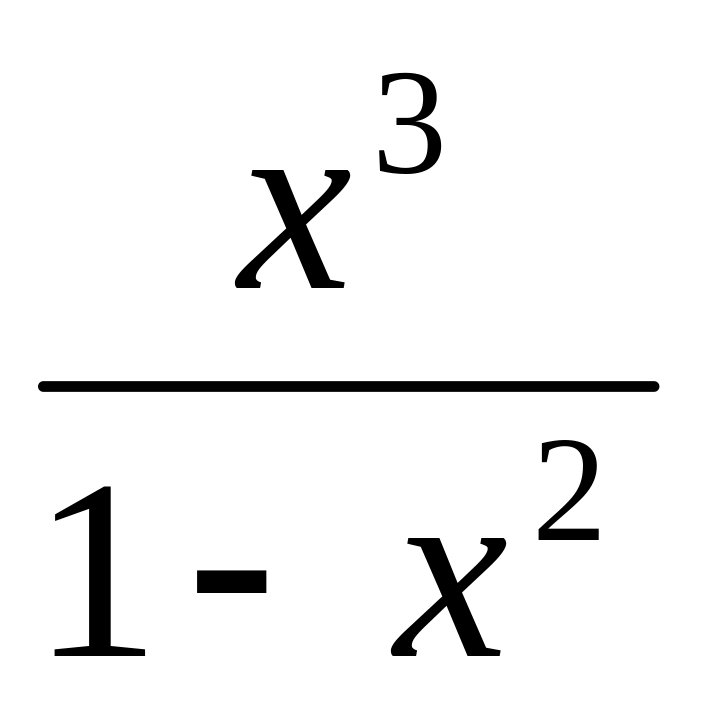 10.
y
=
10.
y
=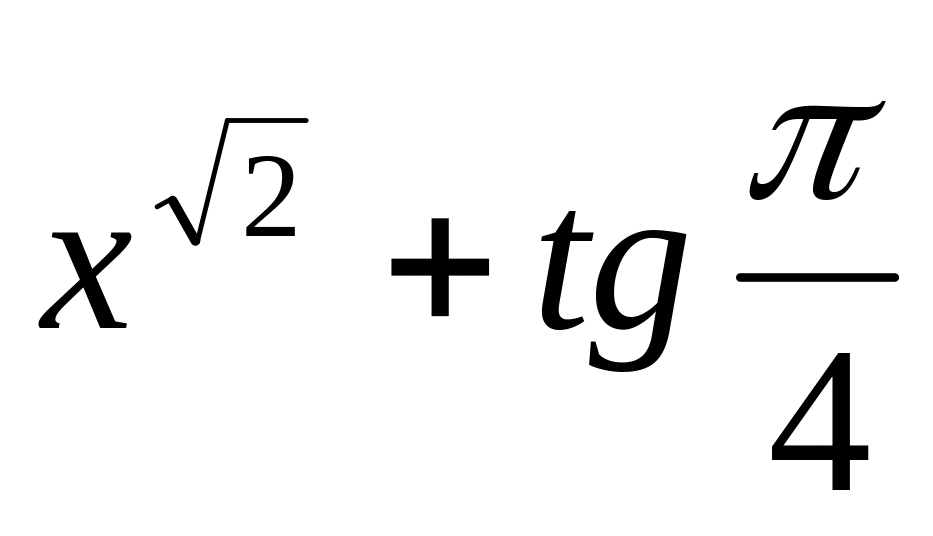
Варіант № 17
y =
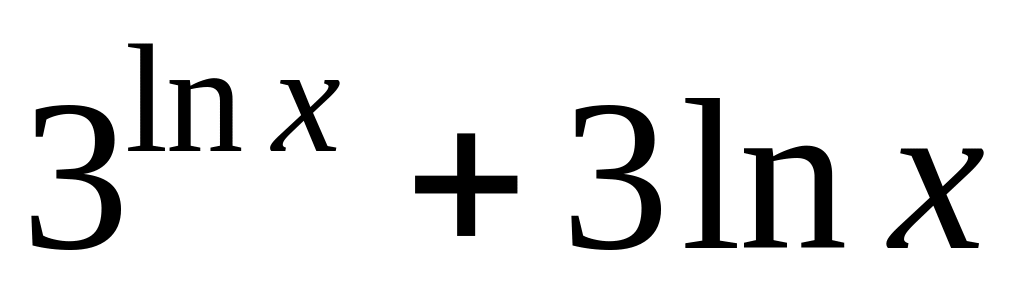 6.
y
=
6.
y
=
S(t) =
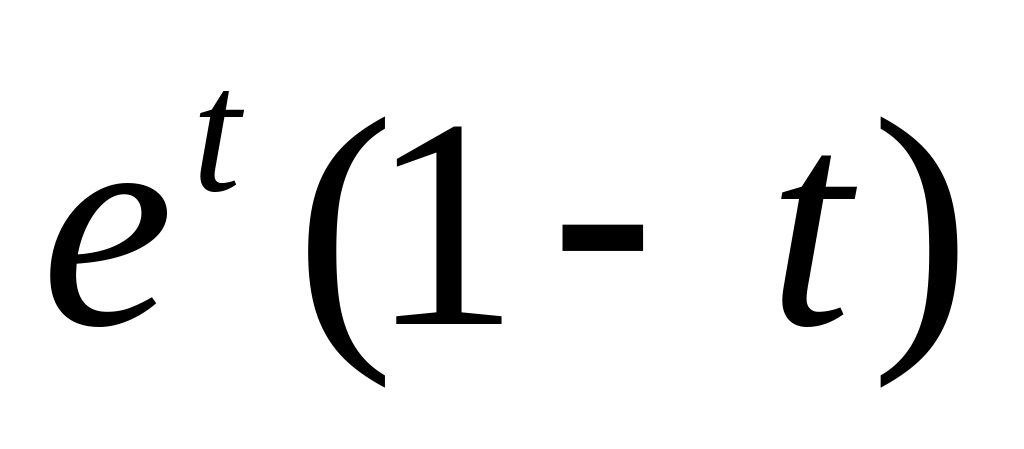 7.
y
=
7.
y
=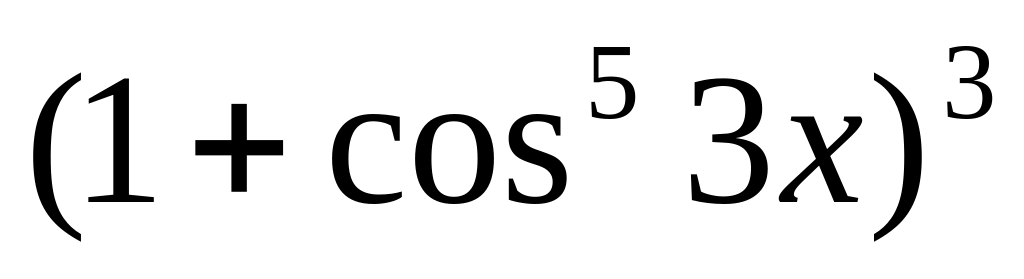
y =
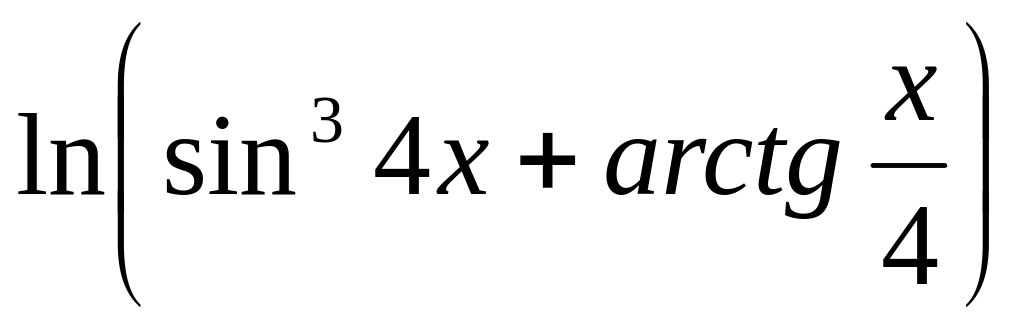 8.
y
=
8.
y
=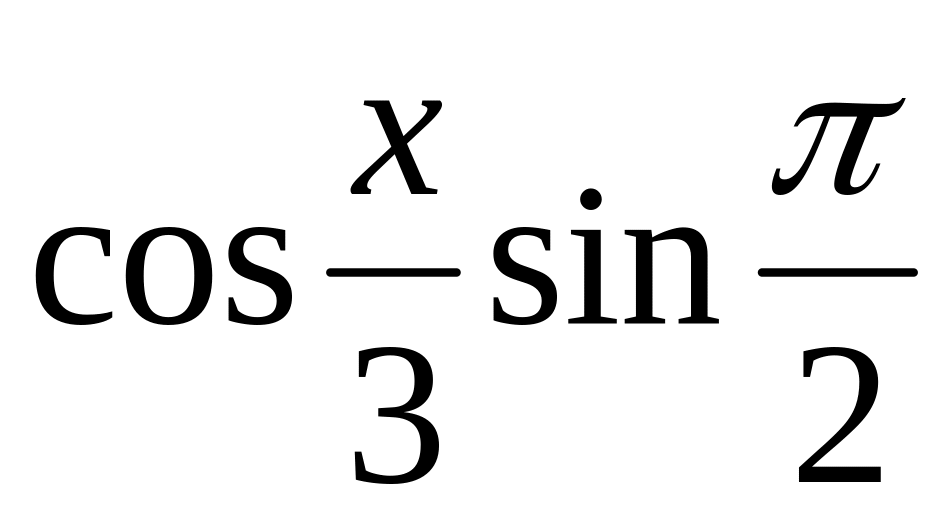
y =
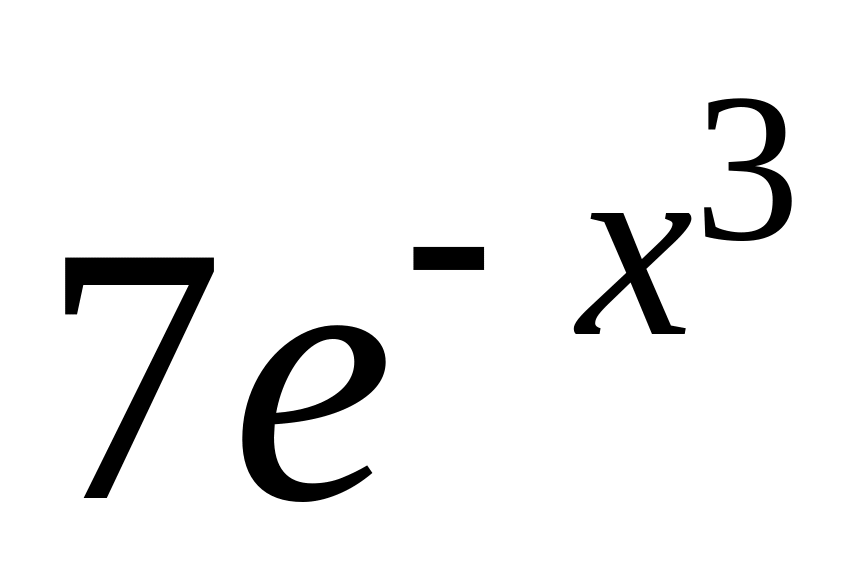 9.
r(
)
=
9.
r(
)
=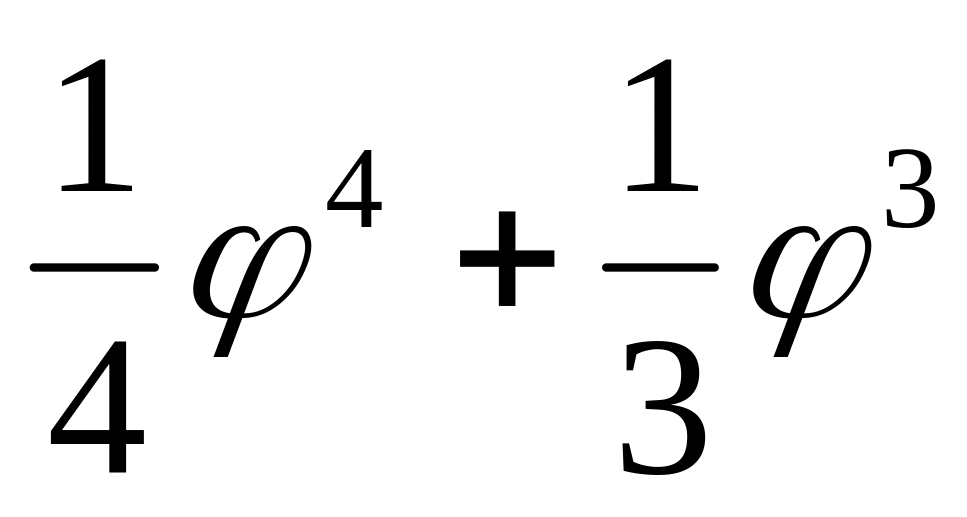
y =
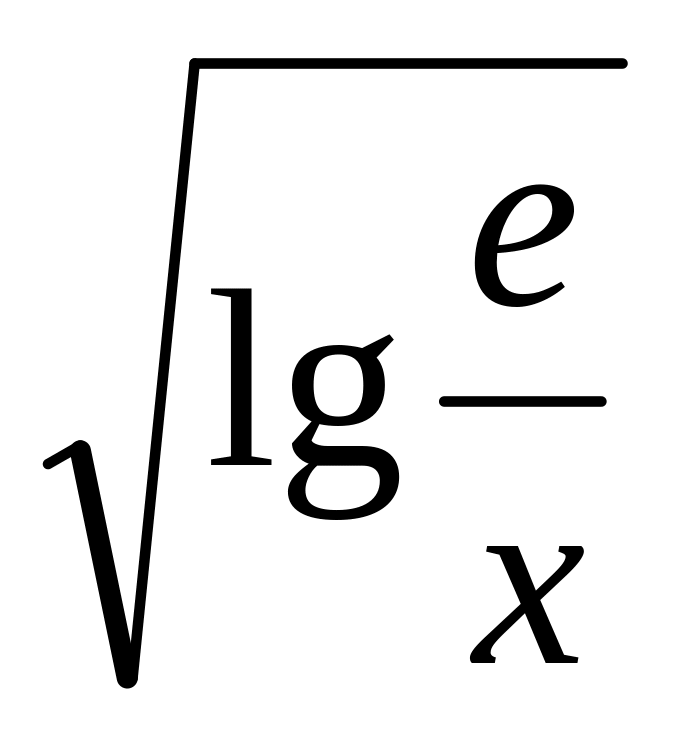 10.
y
=
10.
y
=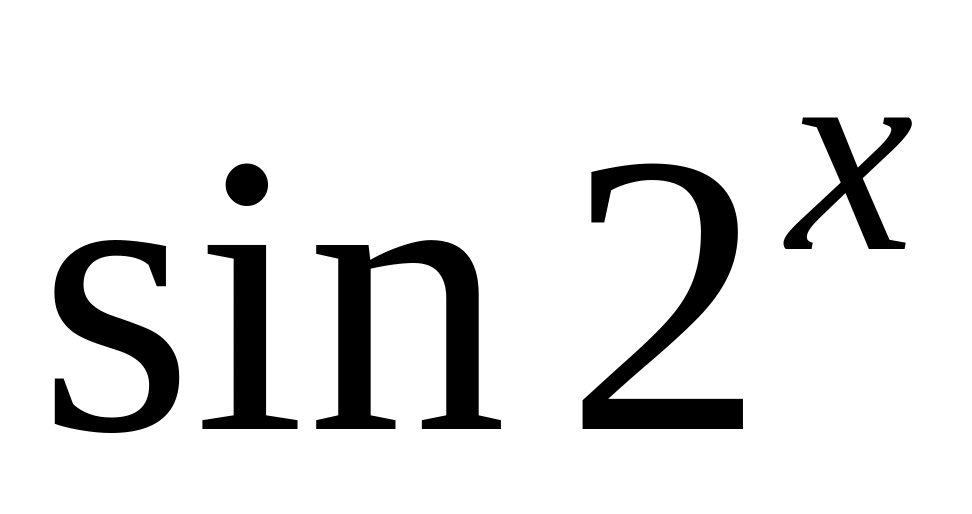
Варіант № 18
y =
 6.
y
=
6.
y
=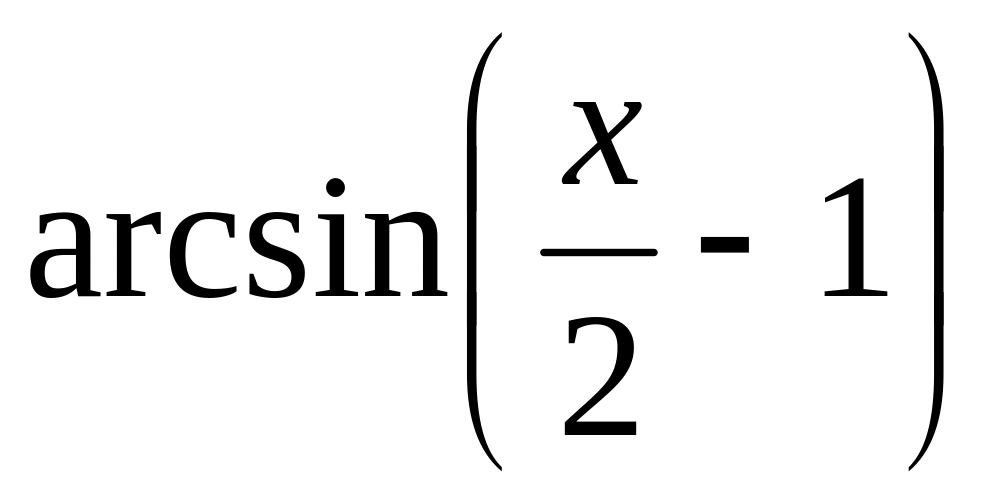
y =
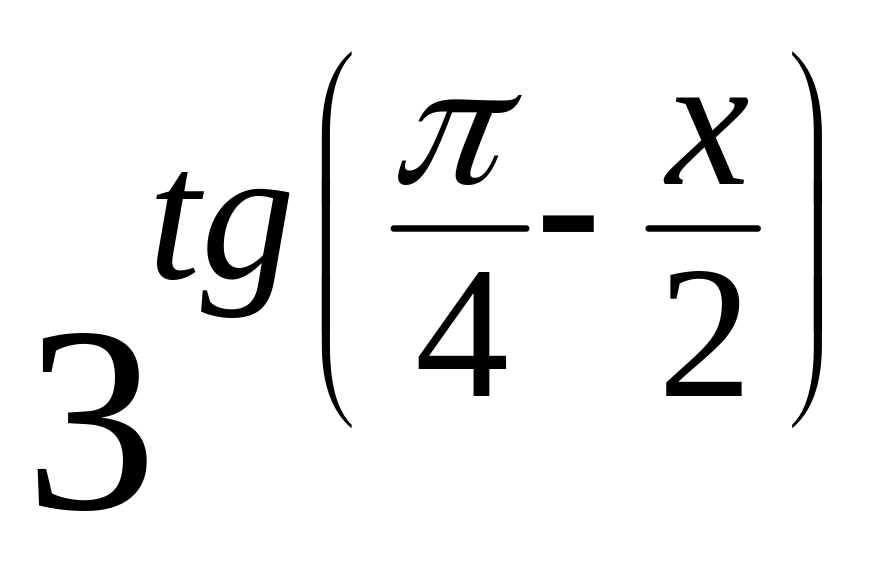 7.
S(t)
=
7.
S(t)
=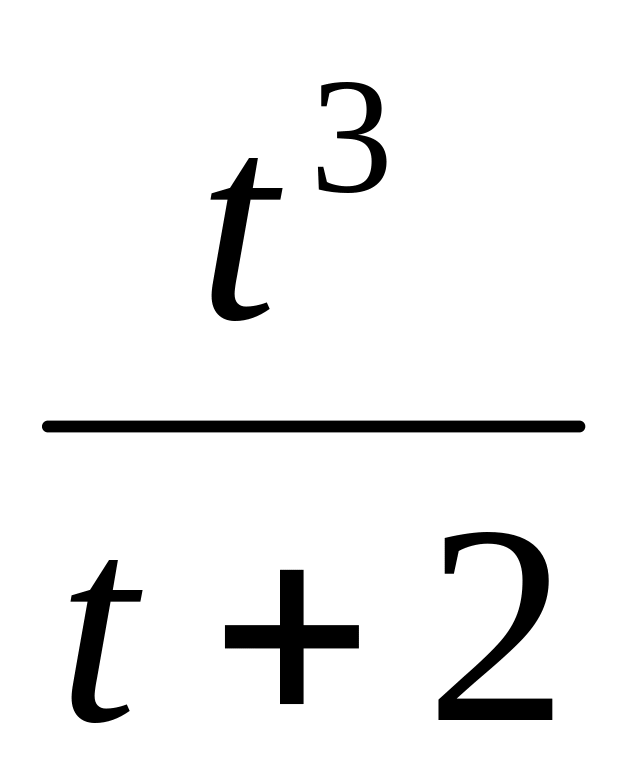
y =
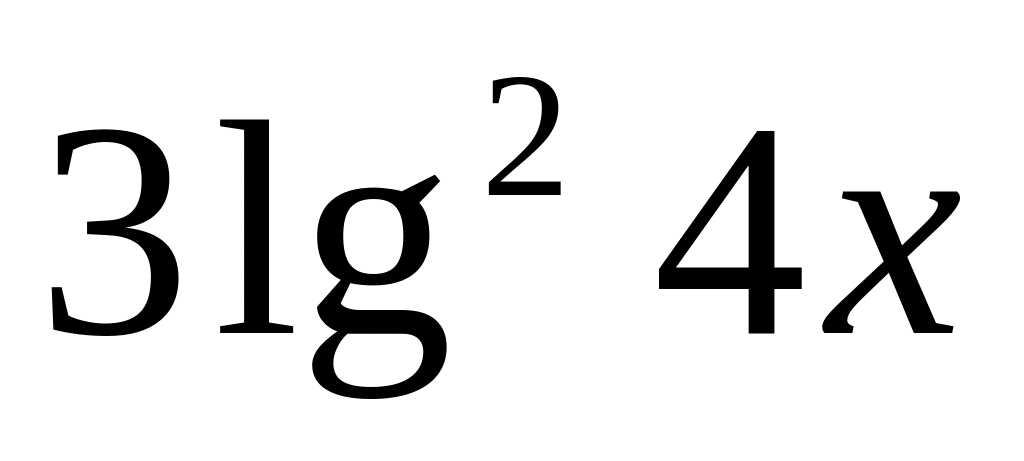 8.
y
=
8.
y
=
y =
 9.
y
= ( 6cos7x+5 )3
9.
y
= ( 6cos7x+5 )3y =
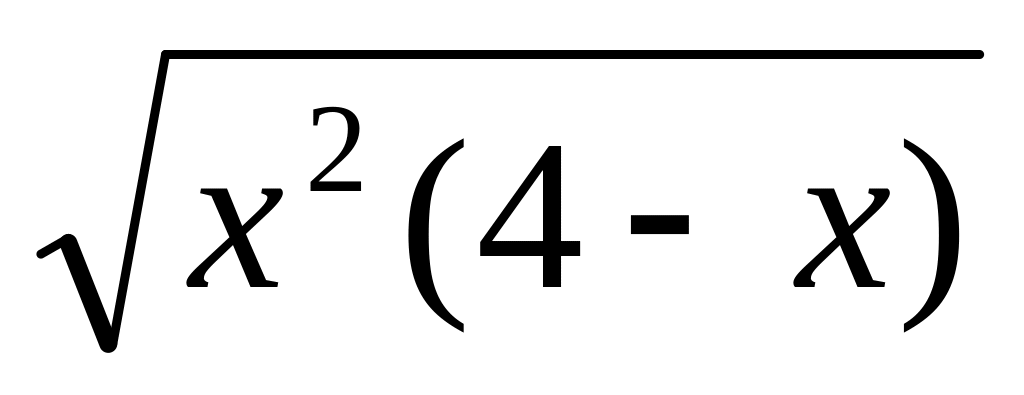 10.
y
=
10.
y
=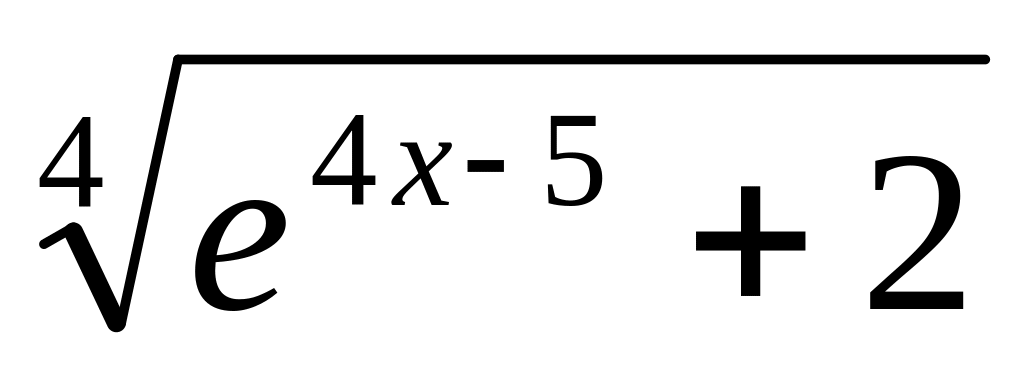
Варіант № 19
y =
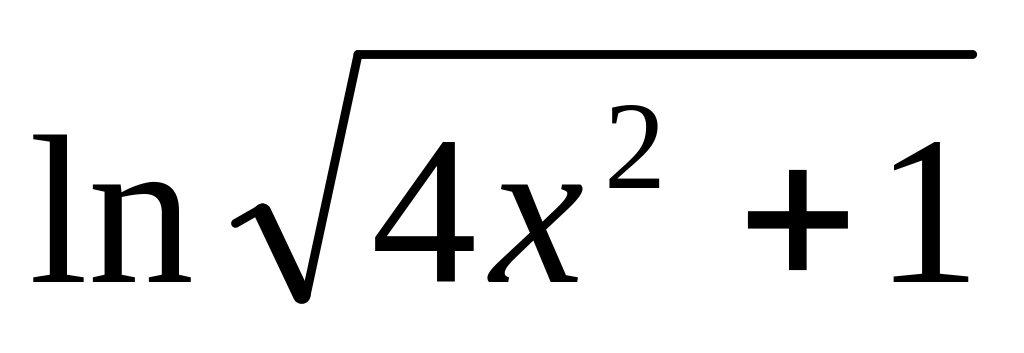 6.
y
=
6.
y
=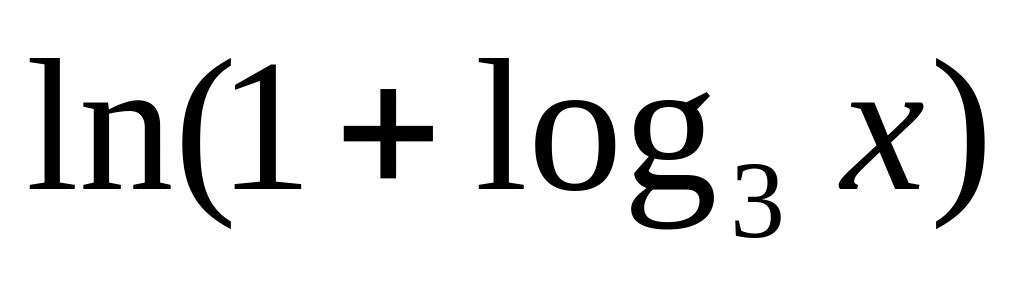
y =
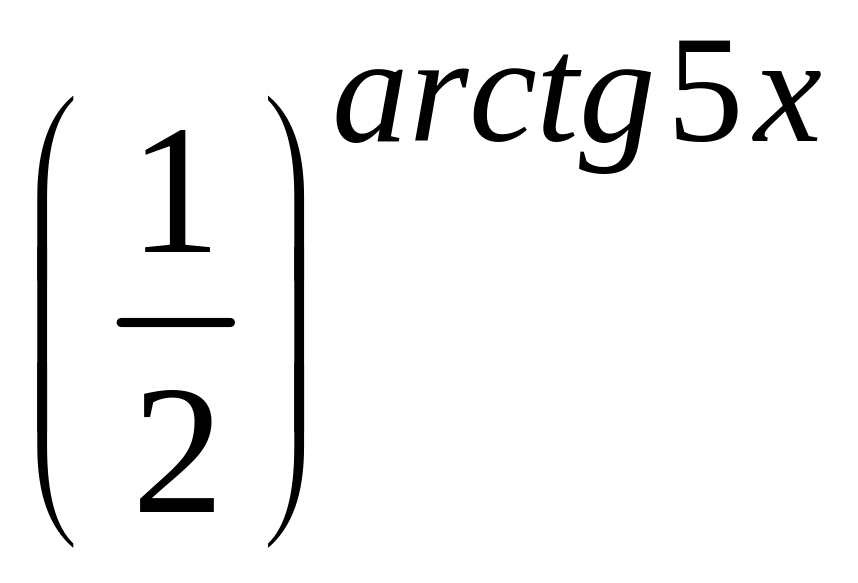 7.
y
=
7.
y
=
y =
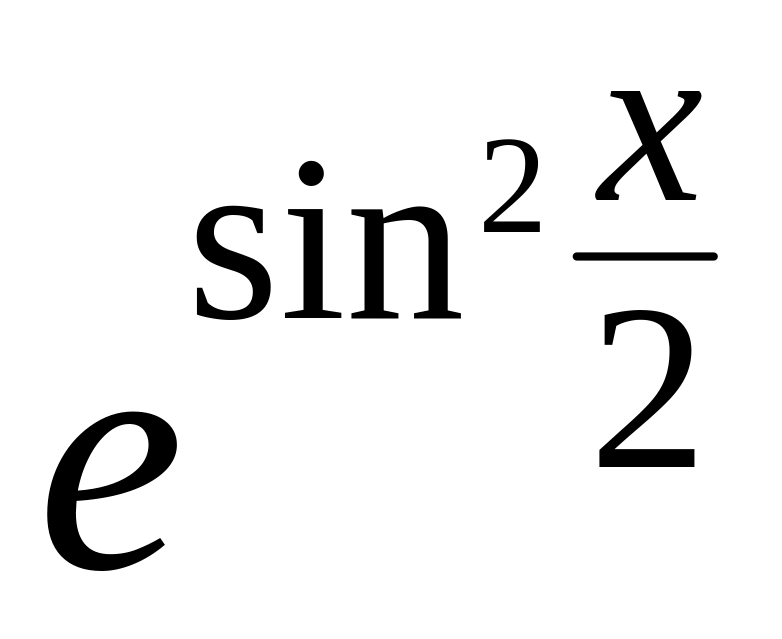 8.
y
=
8.
y
=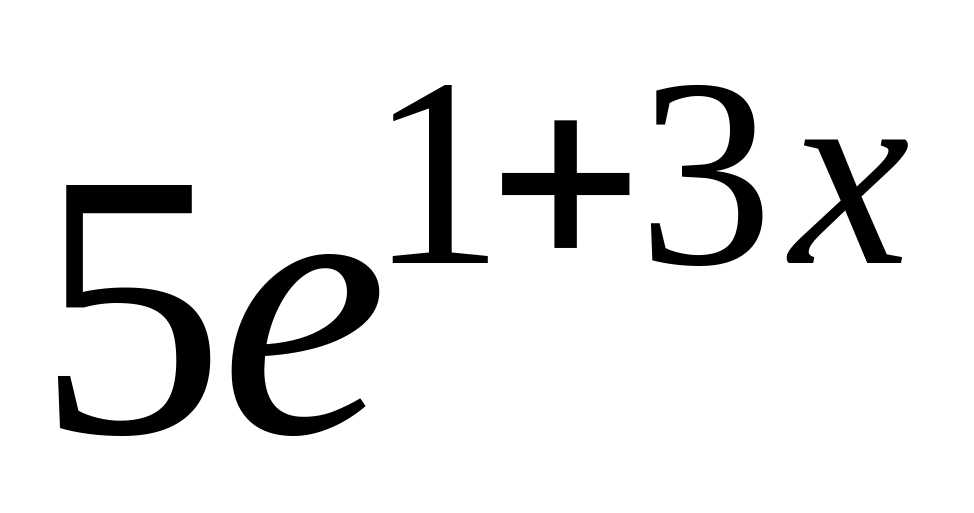
y =
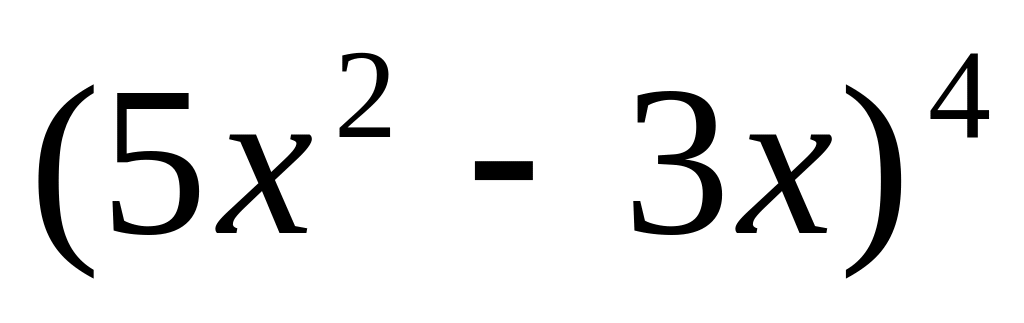 9.
y
=
9.
y
=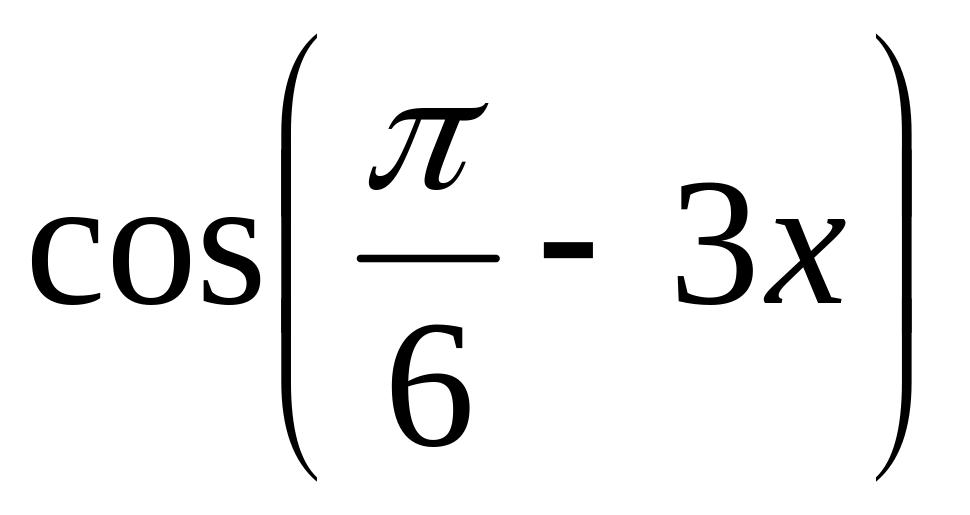
y =3
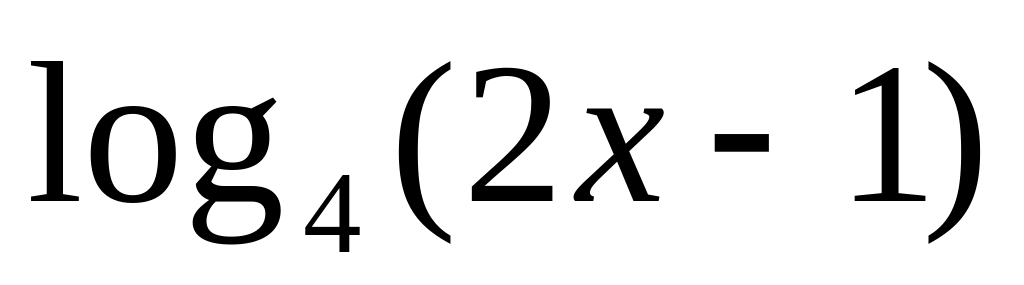 10.
S(t)
=
10.
S(t)
=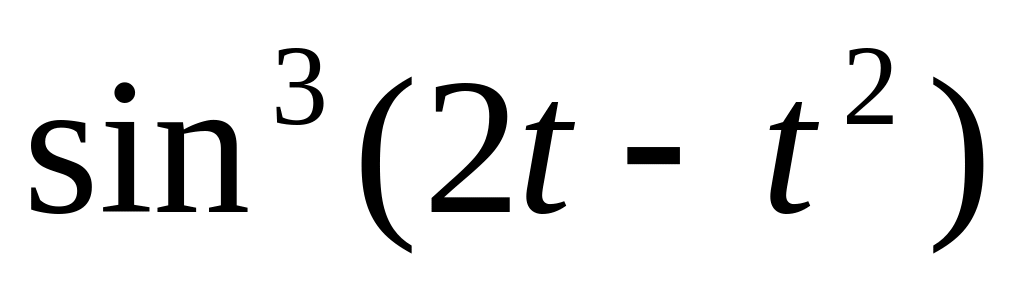
Варіант № 20
y = 6. y =
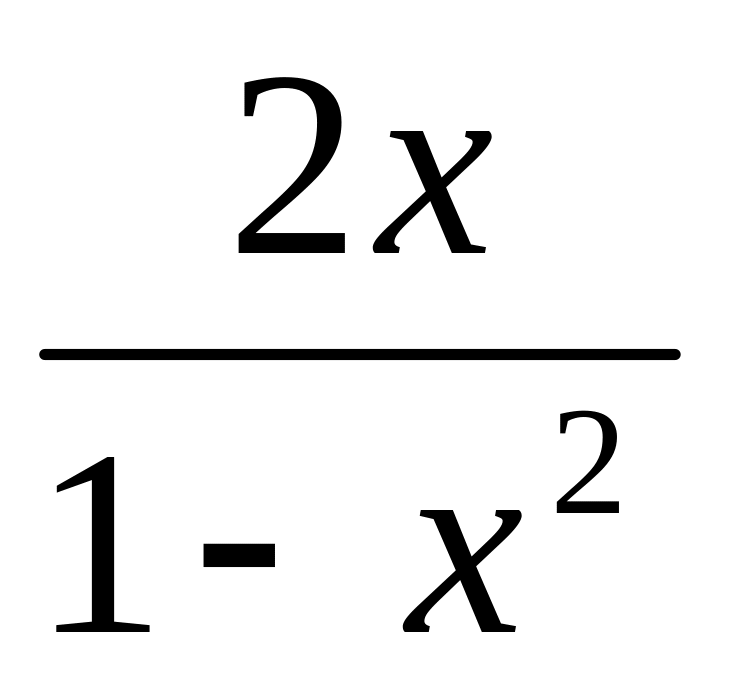
y =
 7.
y
=
7.
y
=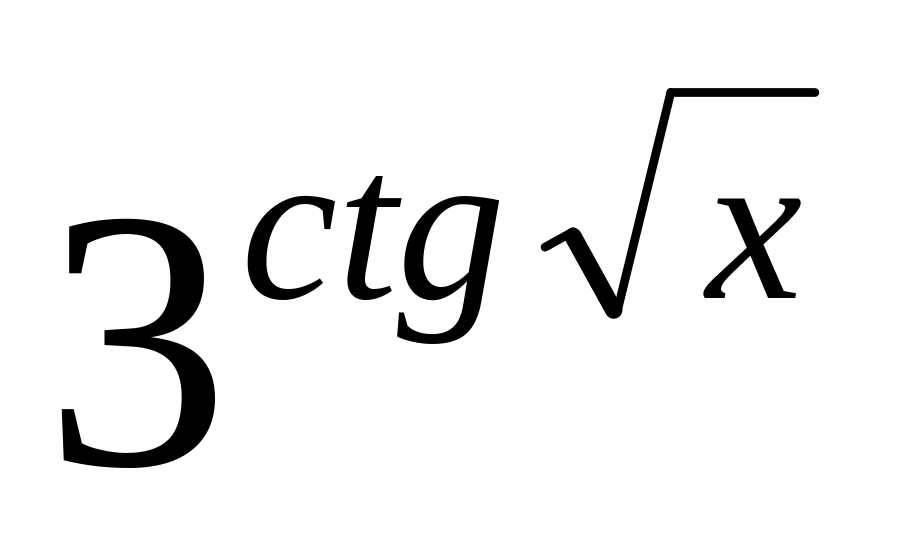
y =
 8.
S(t)
=
8.
S(t)
=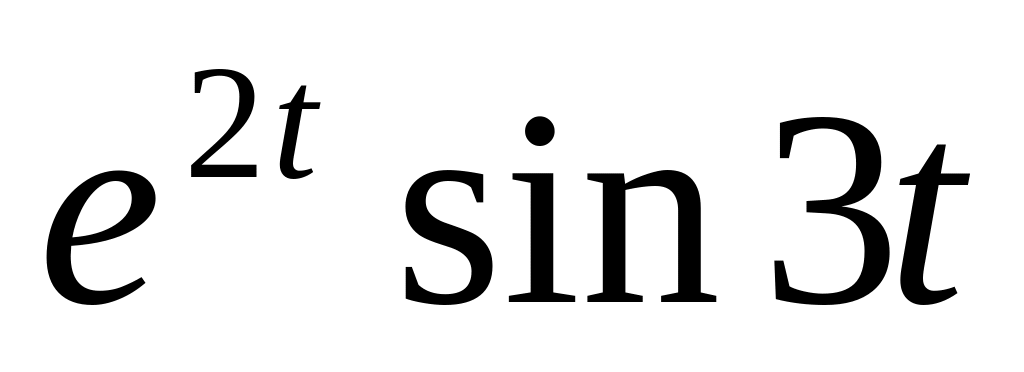
r( ) =
 9.
y
=
9.
y
=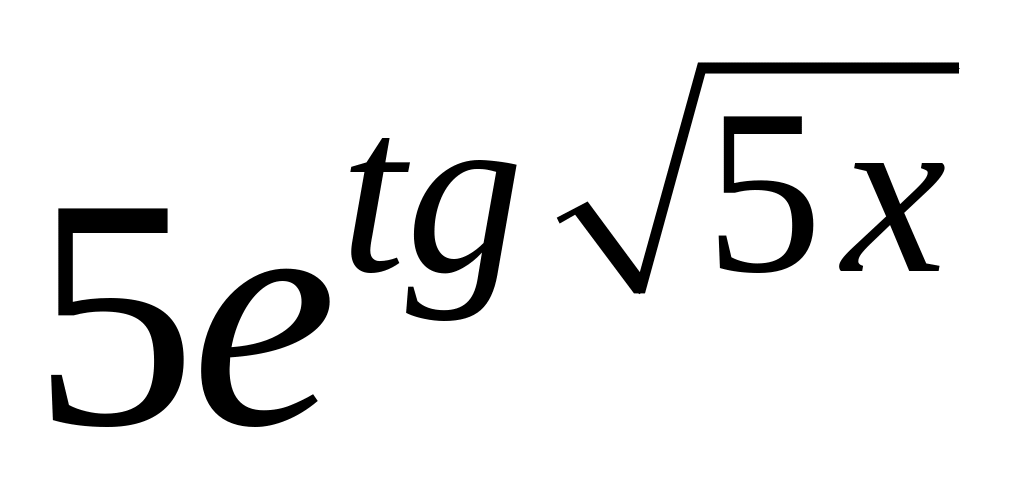
y =
 10.
y
=
10.
y
=
Варіант № 21
y =
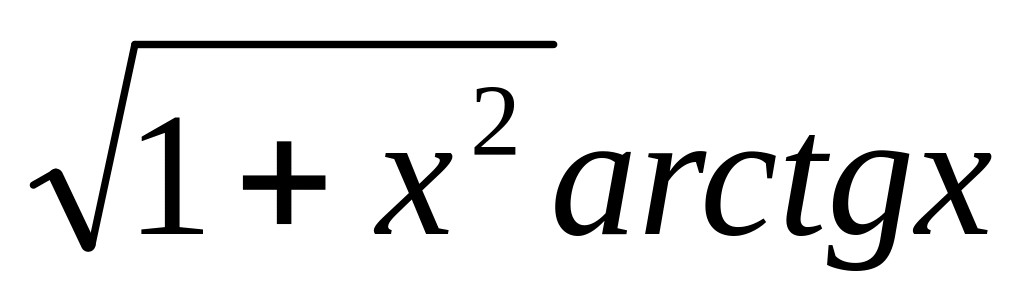 6.
y
=
6.
y
=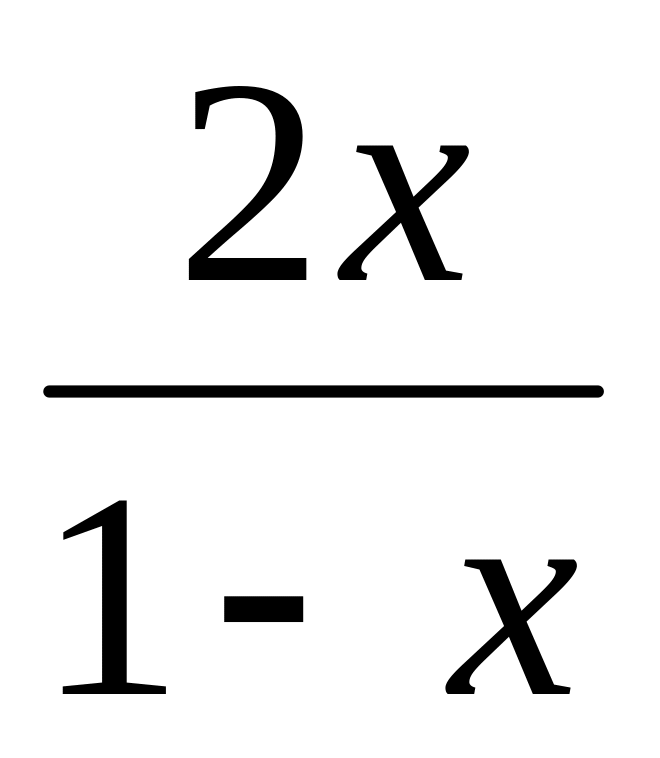
y =
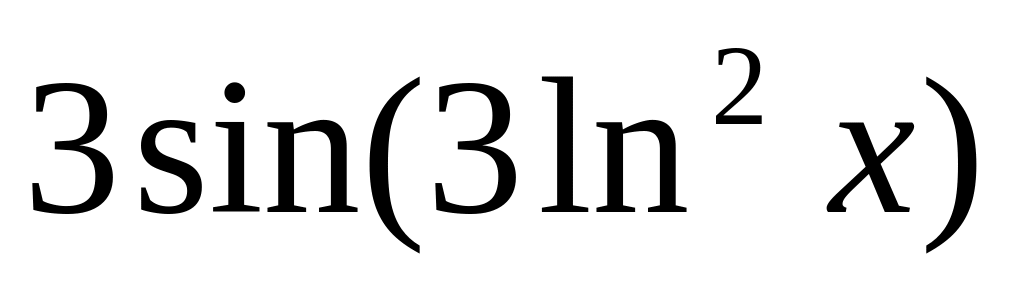 7.
y
=
7.
y
=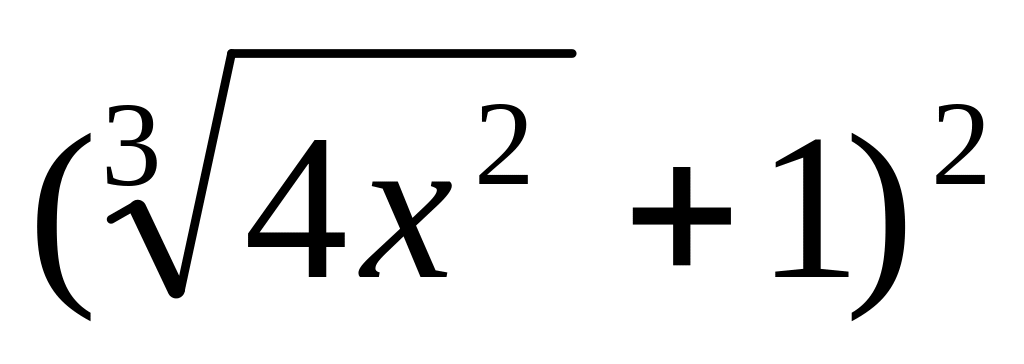
y =
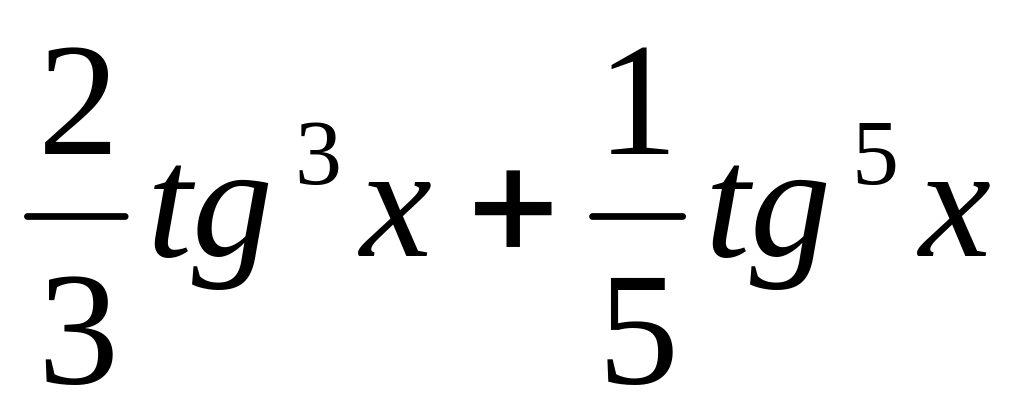 8.
y
=
8.
y
=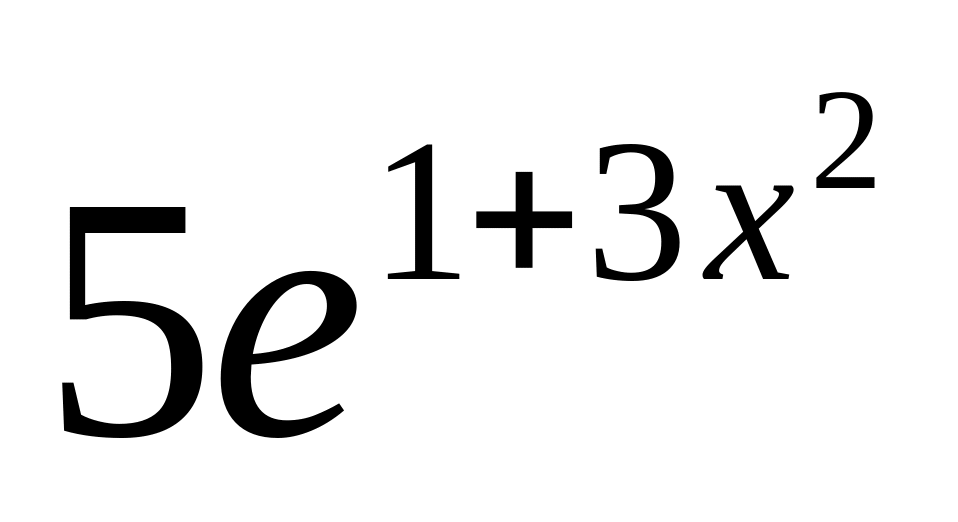
y =
 9.
y
=
9.
y
=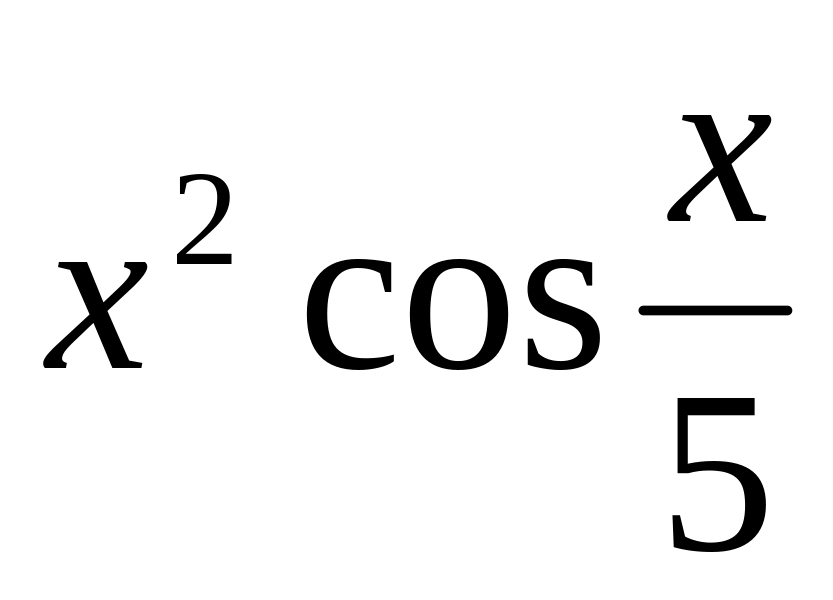
S(t) =
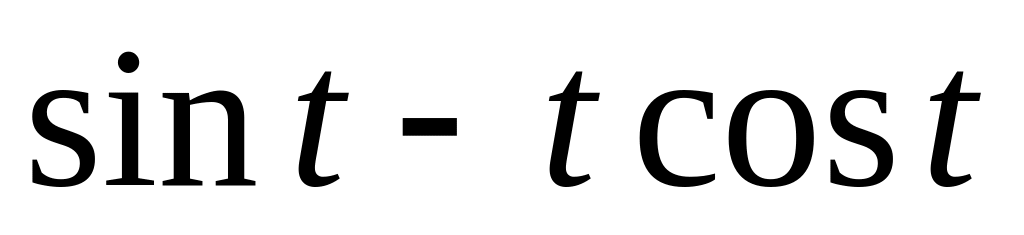 10.
y
=
10.
y
=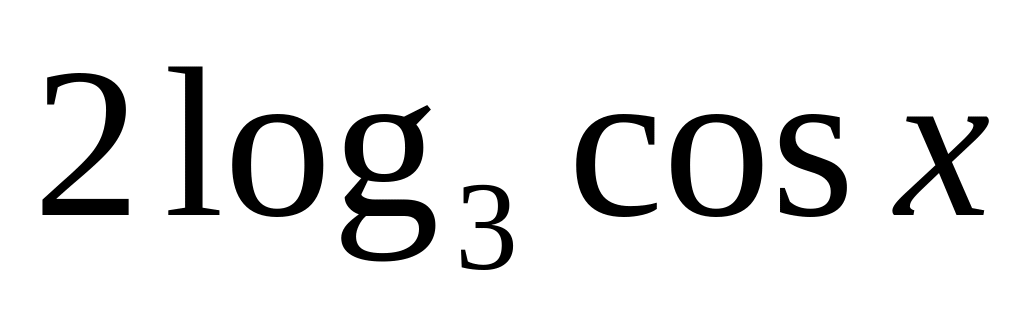
Варіант № 22
r( ) =
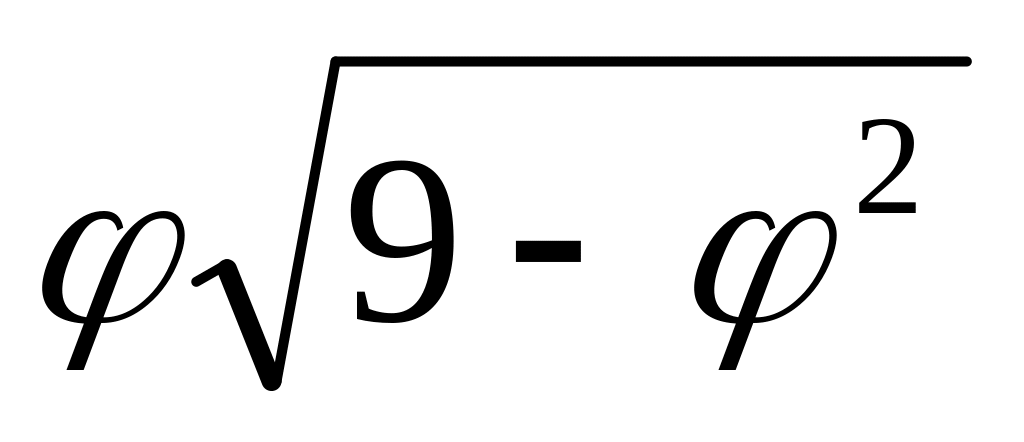 6.
y
=
6.
y
=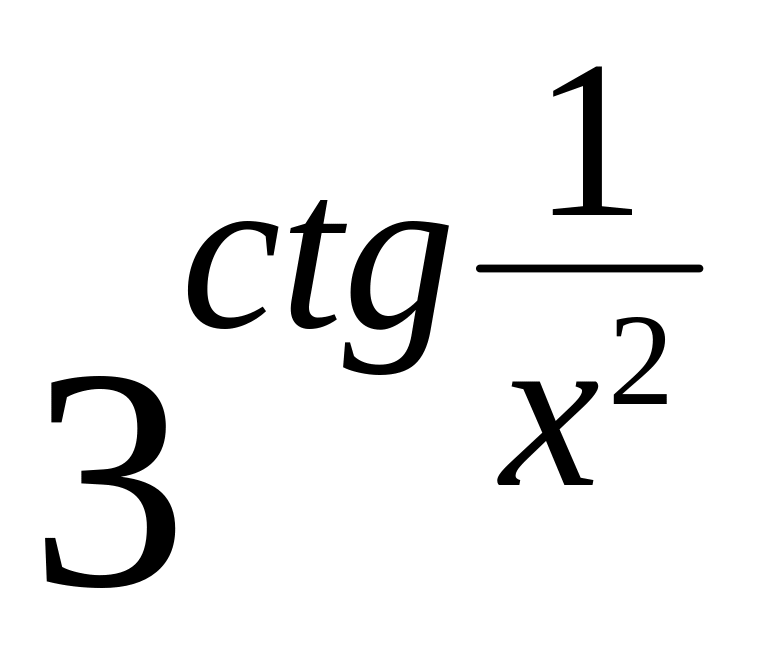
y =
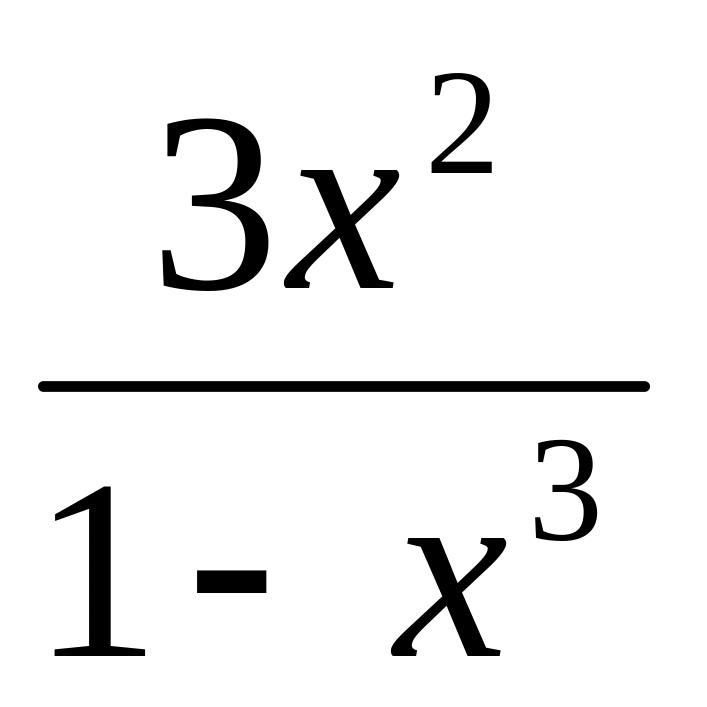 7.
y
=
7.
y
=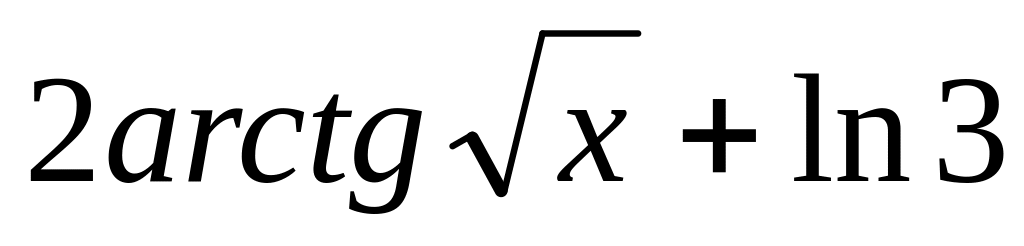
y =
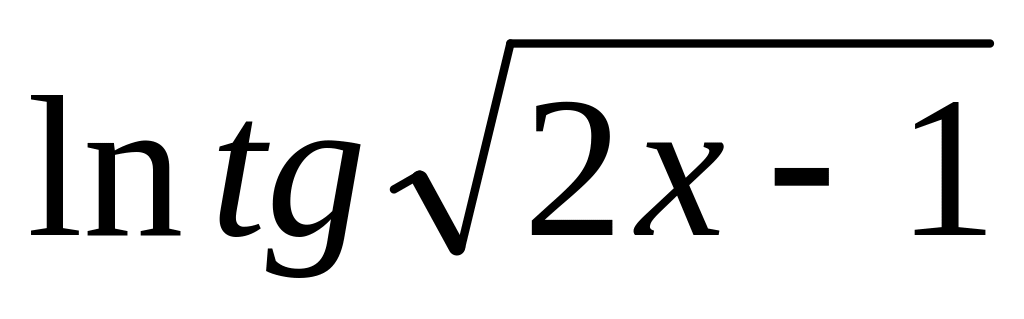 8.
y
=
8.
y
=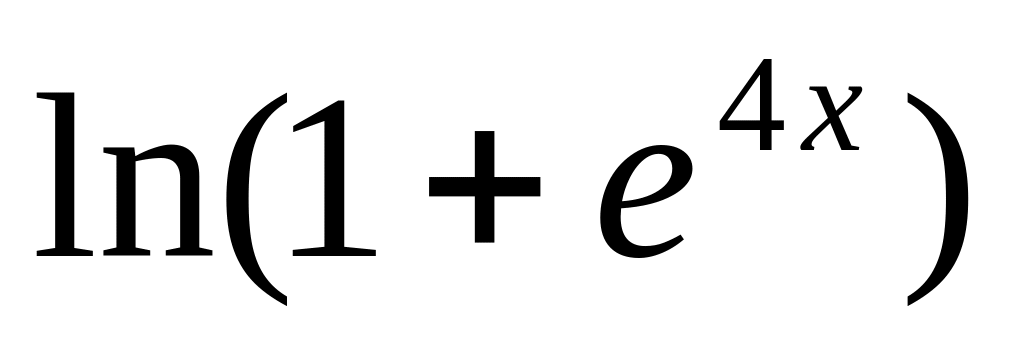
y =
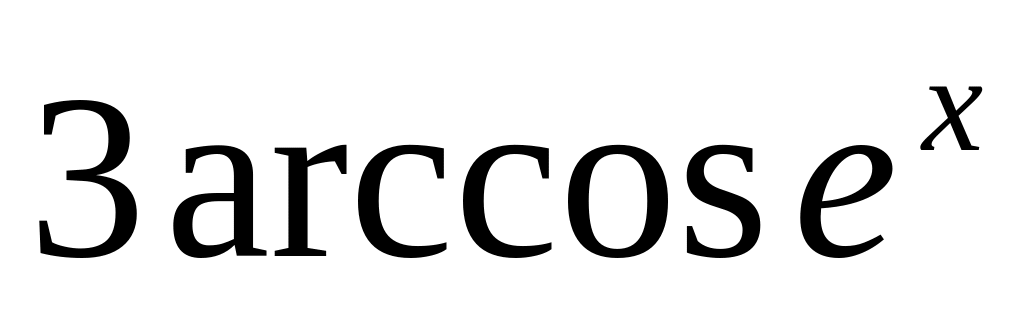 9.
y
=
9.
y
=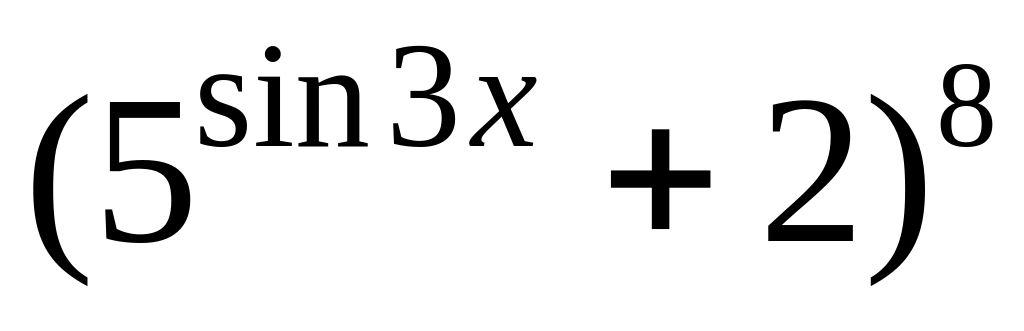
S(t) =
 10.
y
=
10.
y
=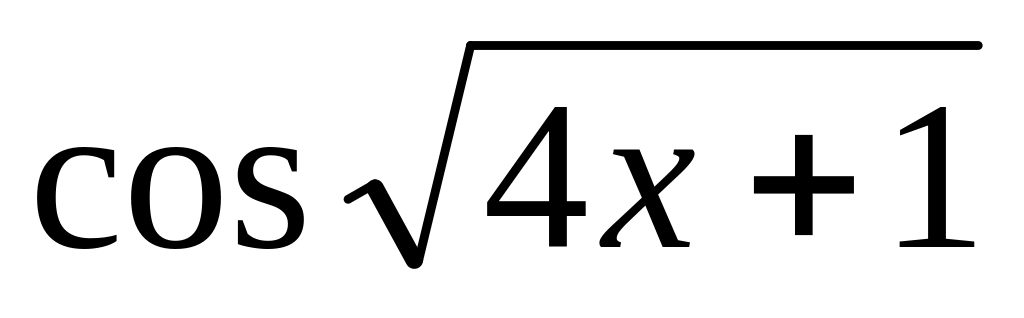
Варіант № 23
y =
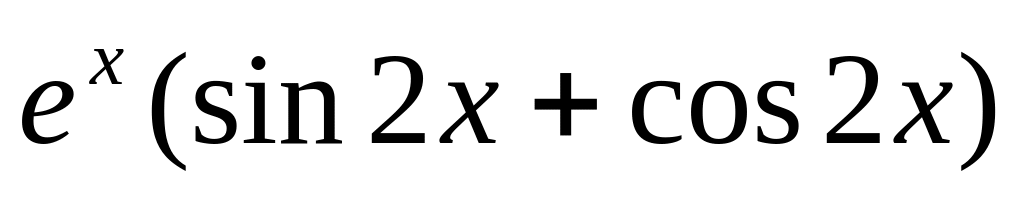 6.
y
=
6.
y
=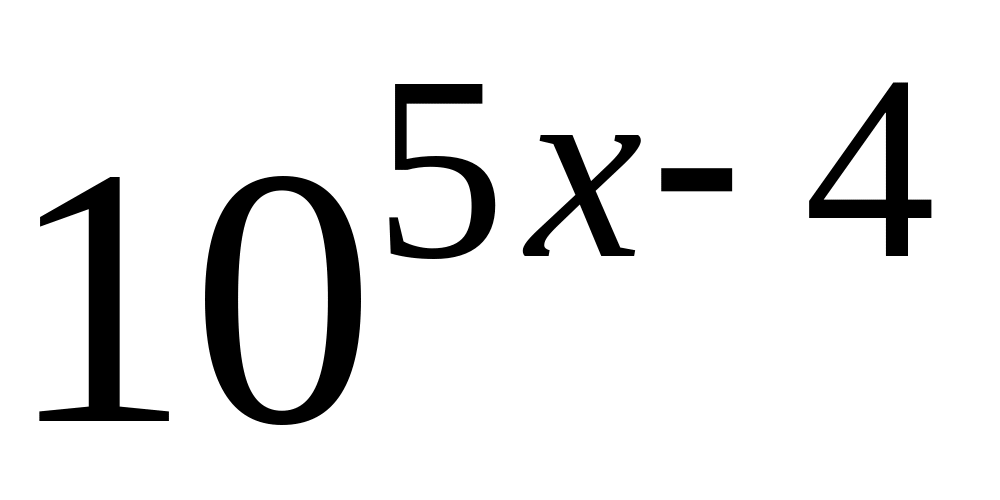
S(t) =
 7.
y
=
7.
y
=
y =
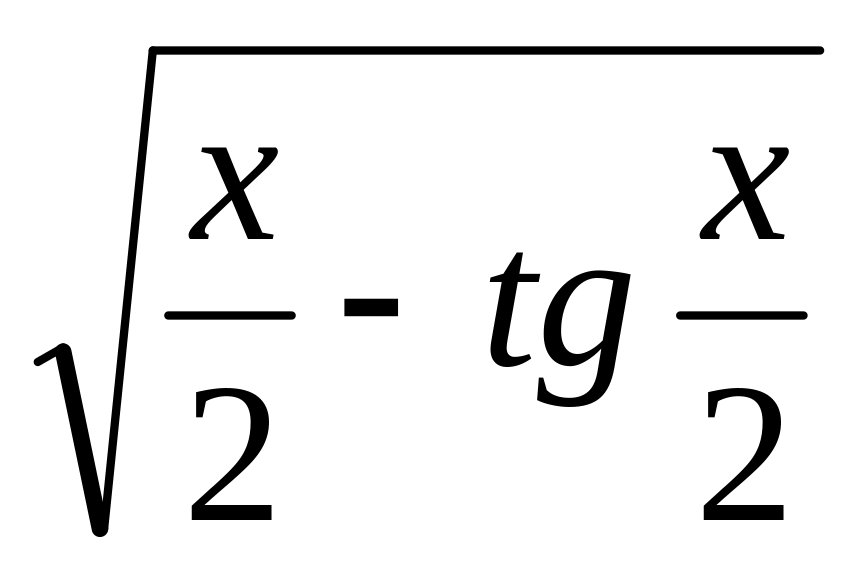 8.
r(
)
=
8.
r(
)
=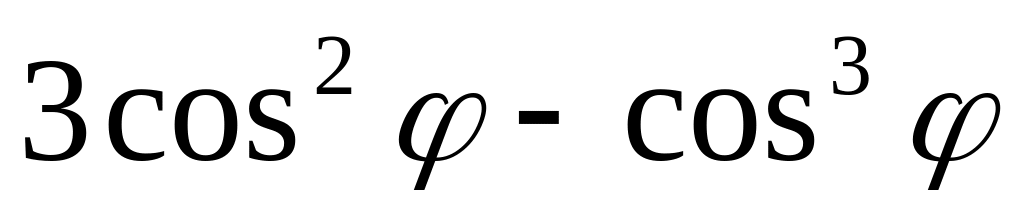
y =
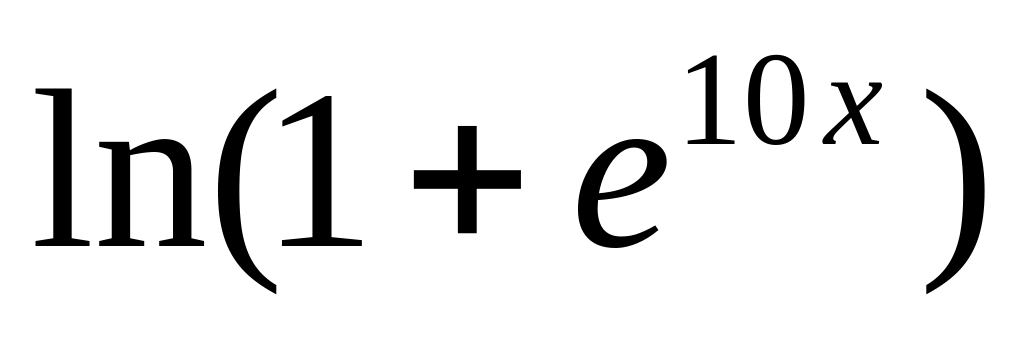 9.
y
=
9.
y
=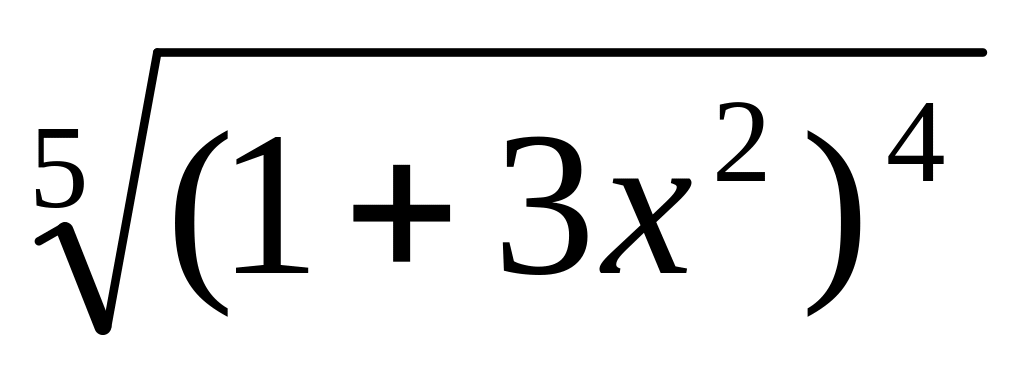
y =
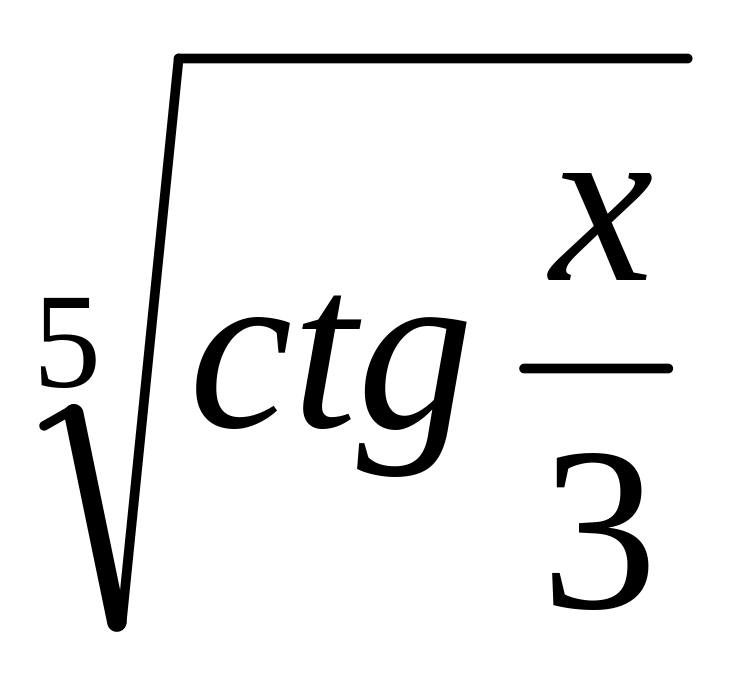 10.
y
=
10.
y
=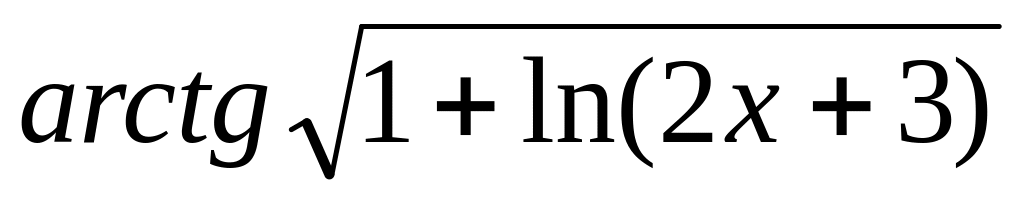
Варіант № 24
S(t) =
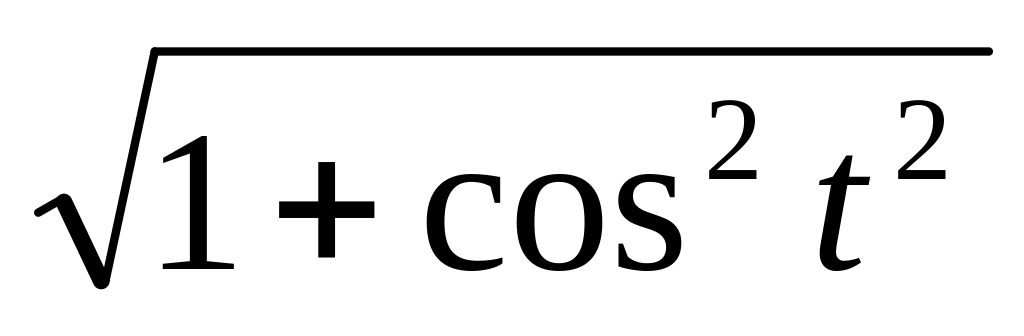 6.
y
=
6.
y
=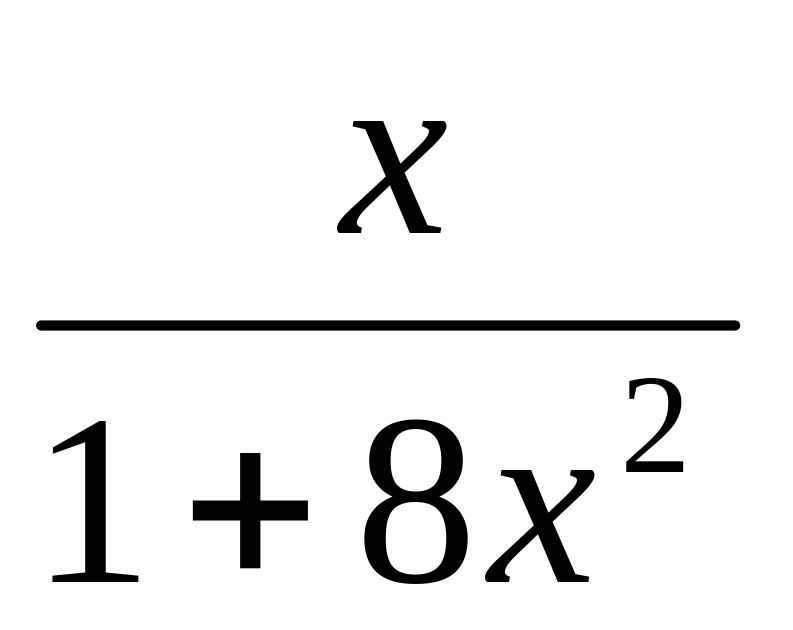
y =
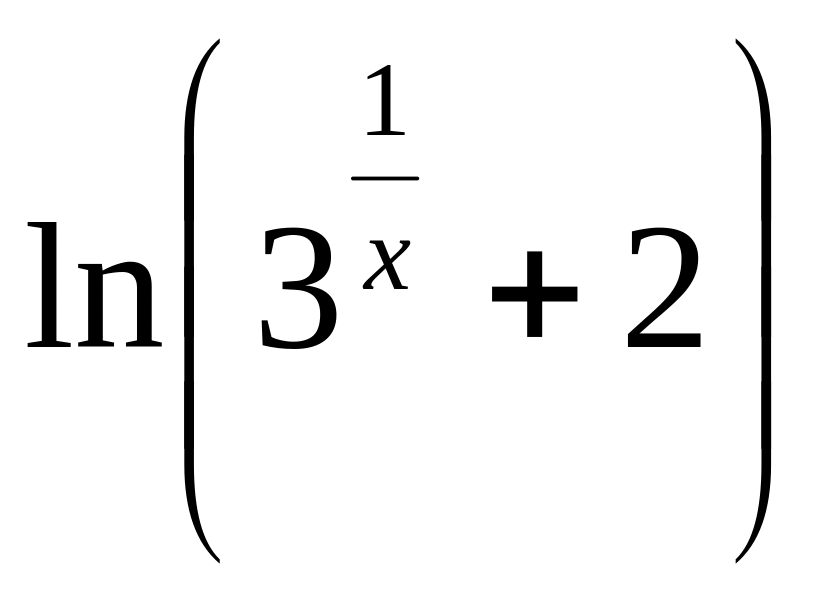 7.
y
=
7.
y
=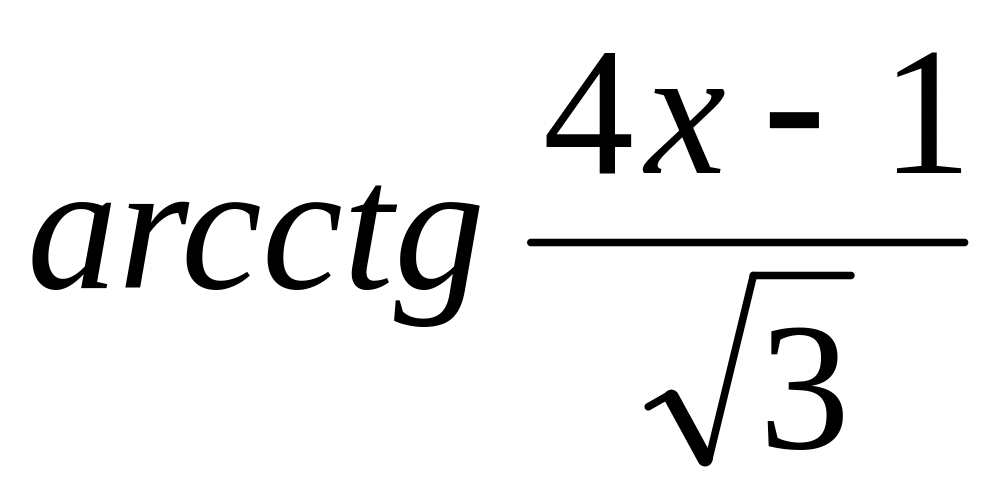
y =
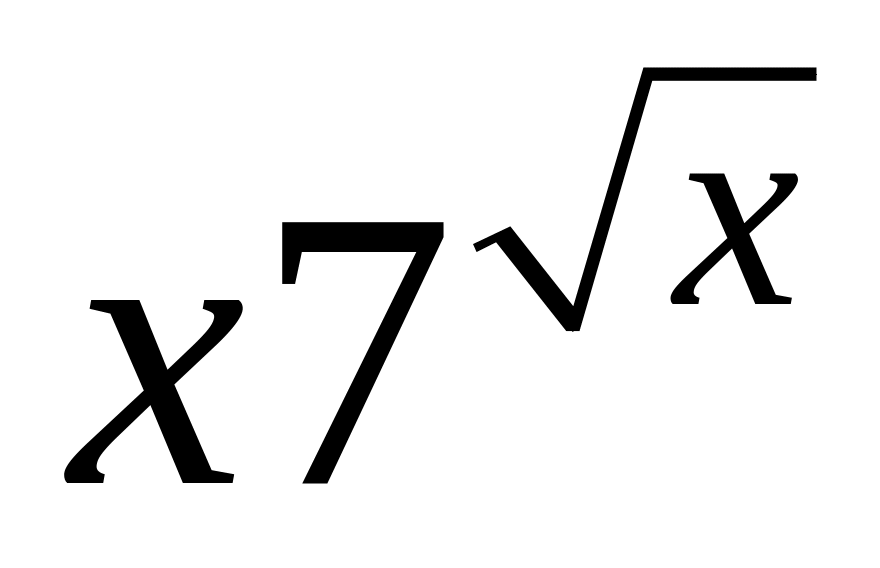 8.
y
=
8.
y
=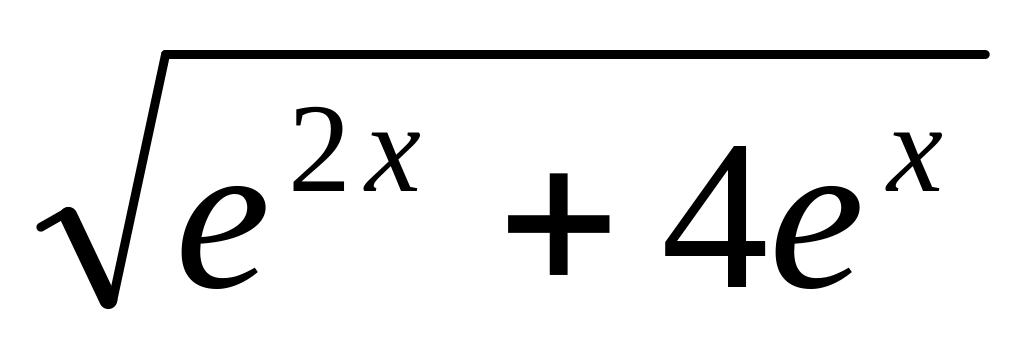
y =
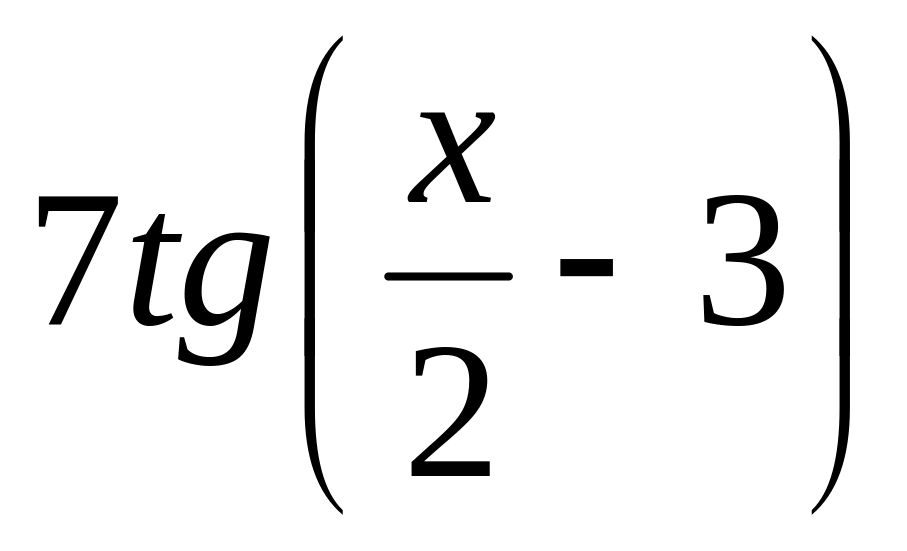 9.
y
=
9.
y
=
y =
 10.
y
=
10.
y
=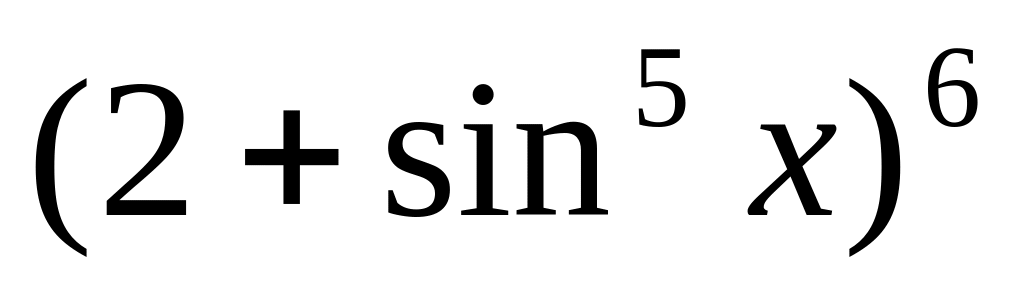
Варіант № 25
y =
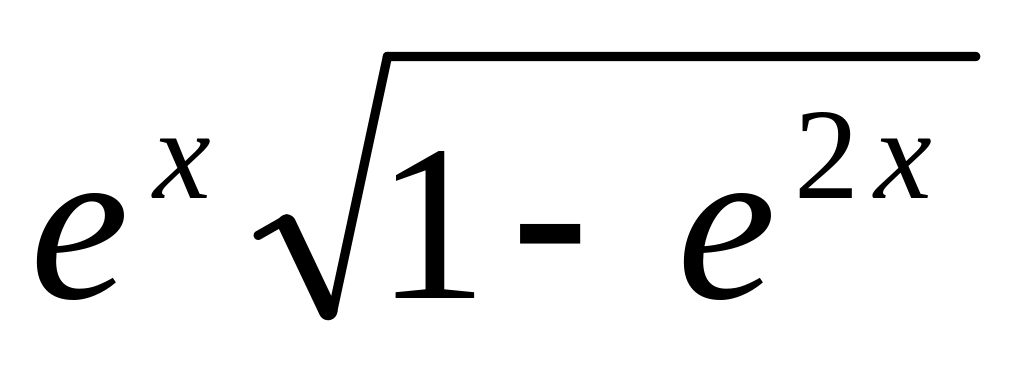 6.
f(t)
=
6.
f(t)
=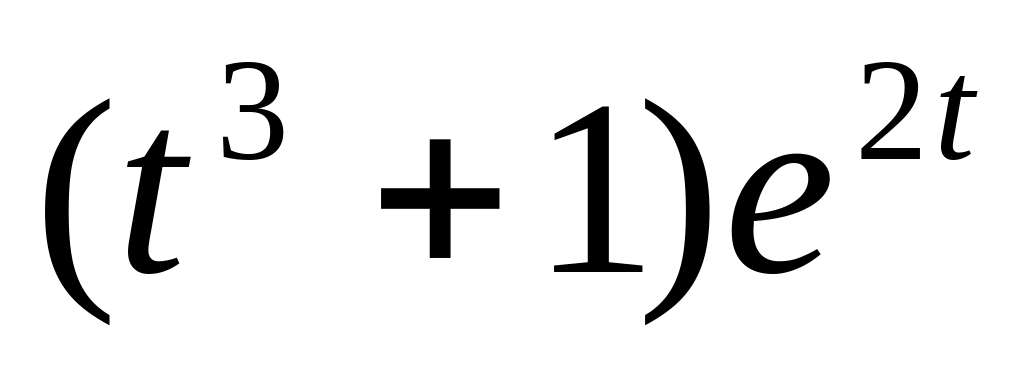
y =
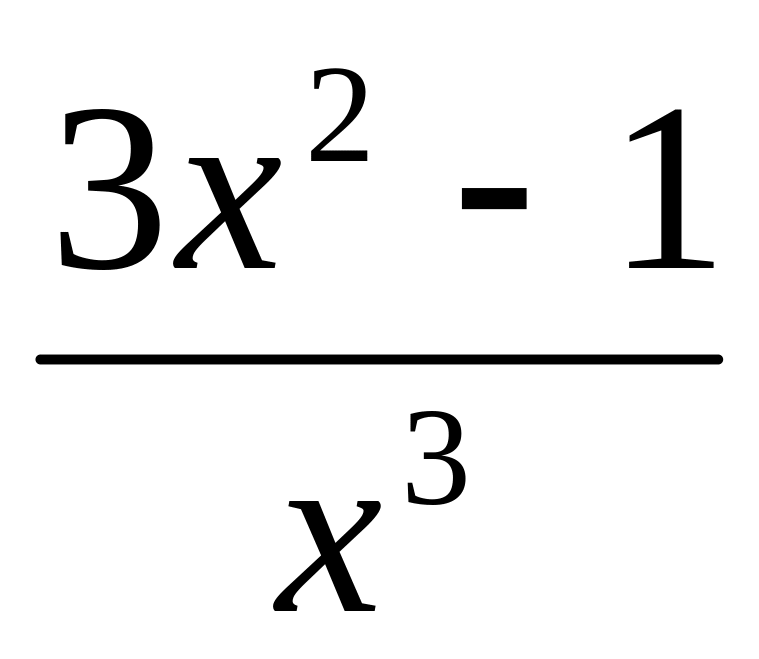 7.
y
=
7.
y
=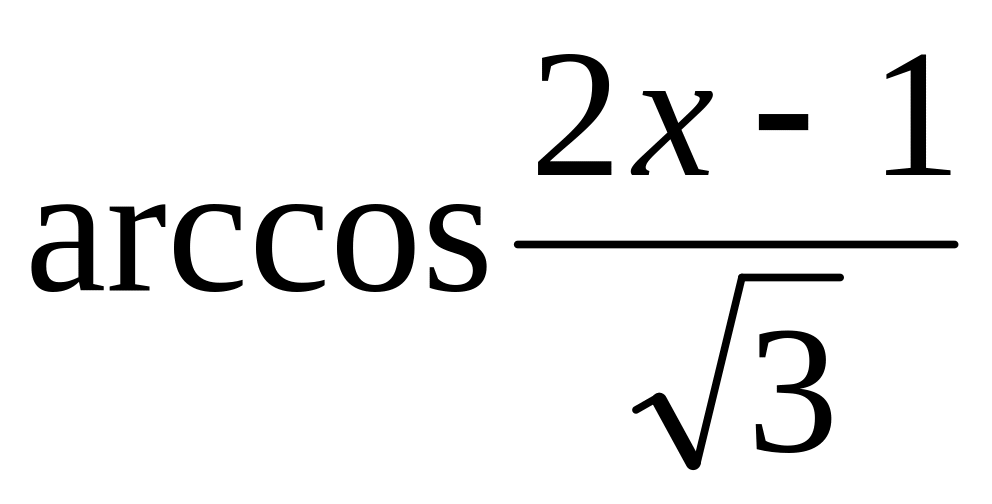
y =
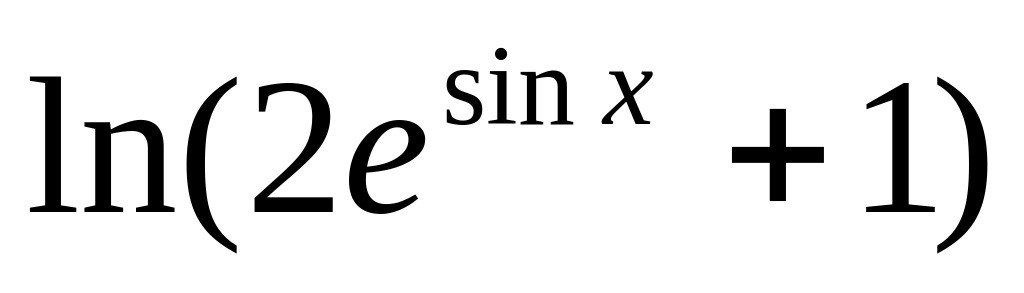 8.
r(
)
=
8.
r(
)
=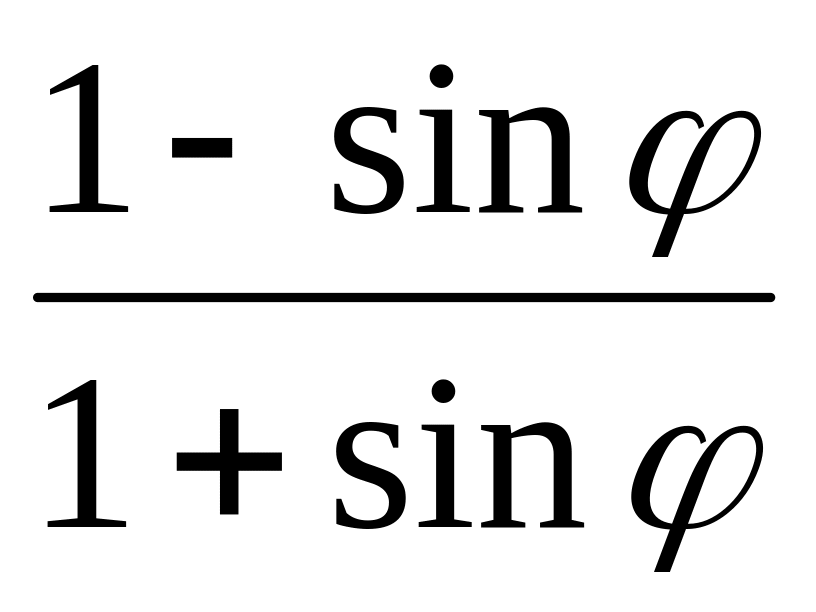
S(t) =
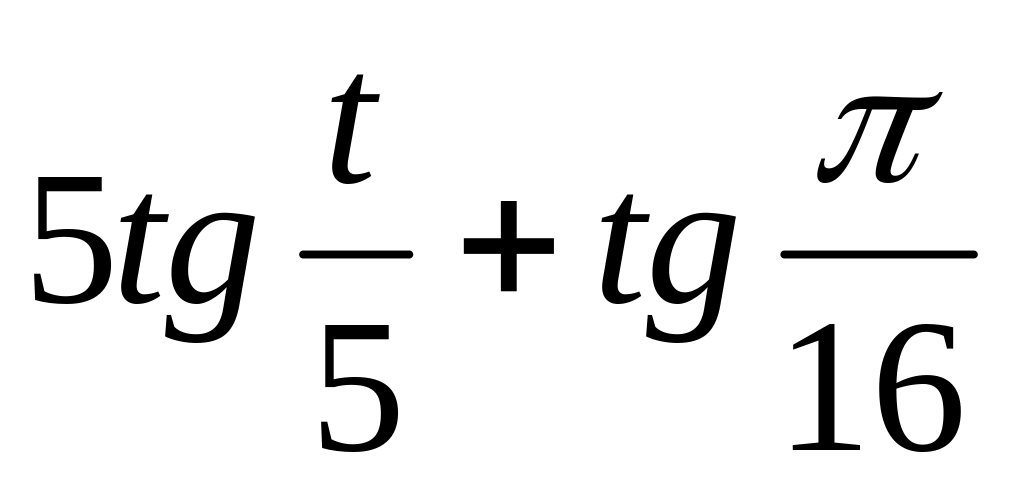 9.
y
=
9.
y
=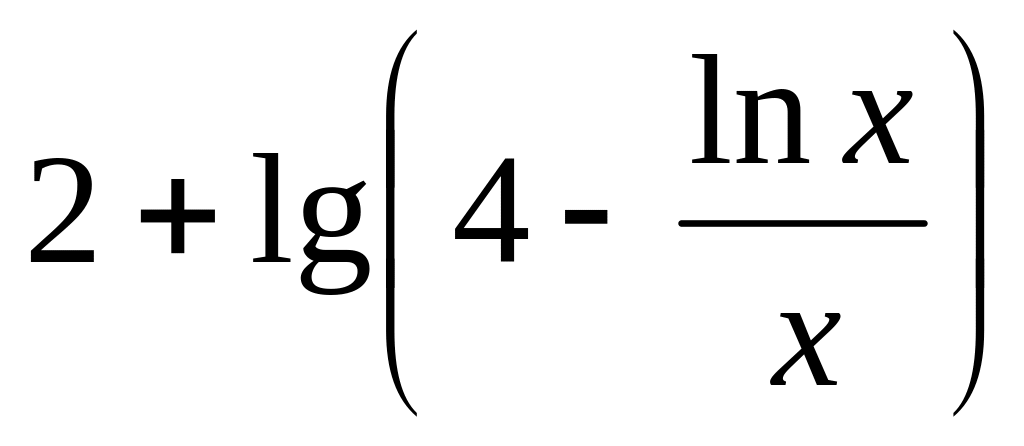
y =
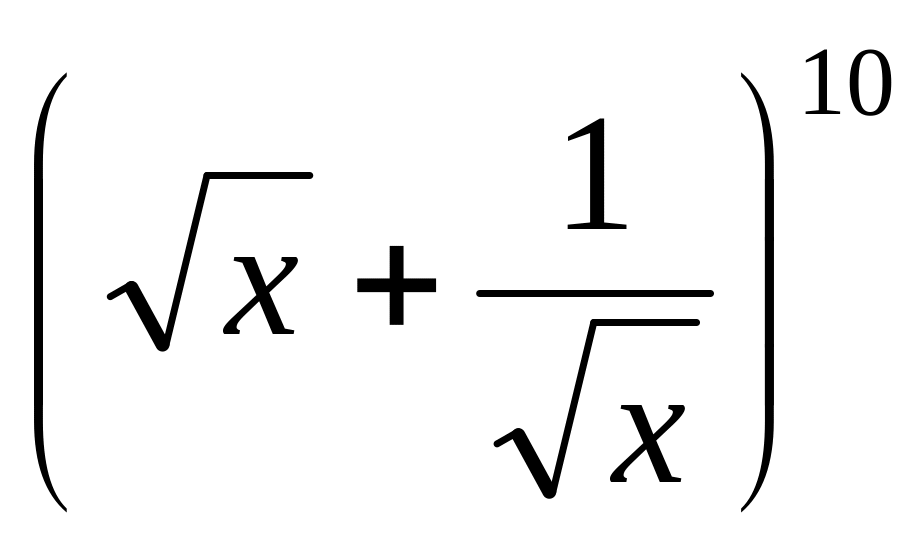 10.
y
=
10.
y
=
Варіант № 26
y =
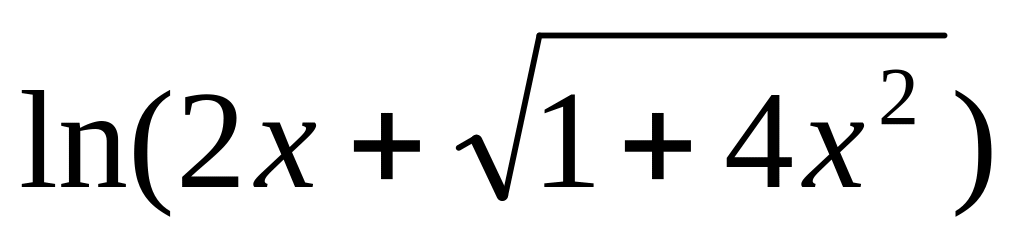 6.
f(t)
=
6.
f(t)
=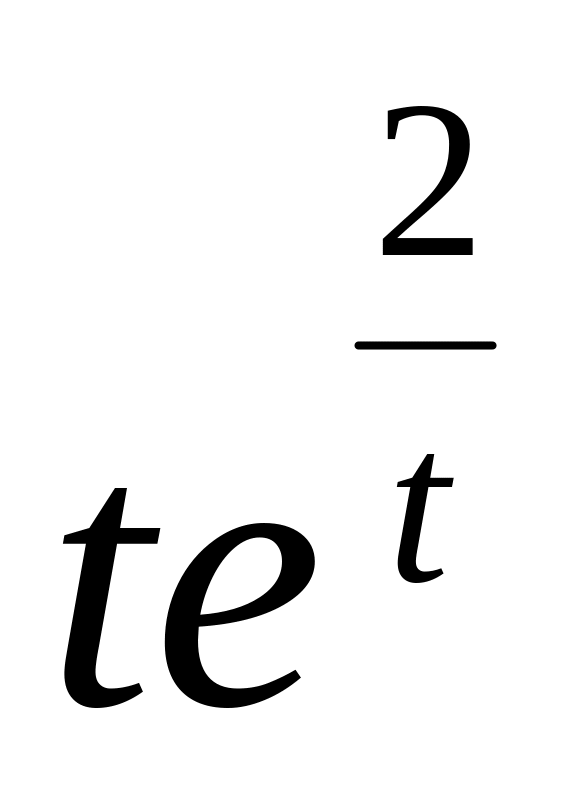
y =
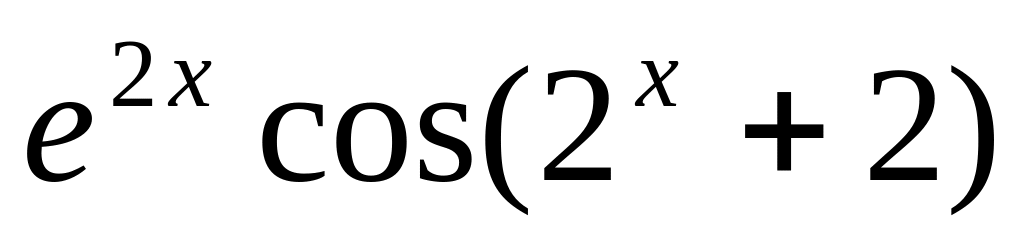 7.
y
=
7.
y
=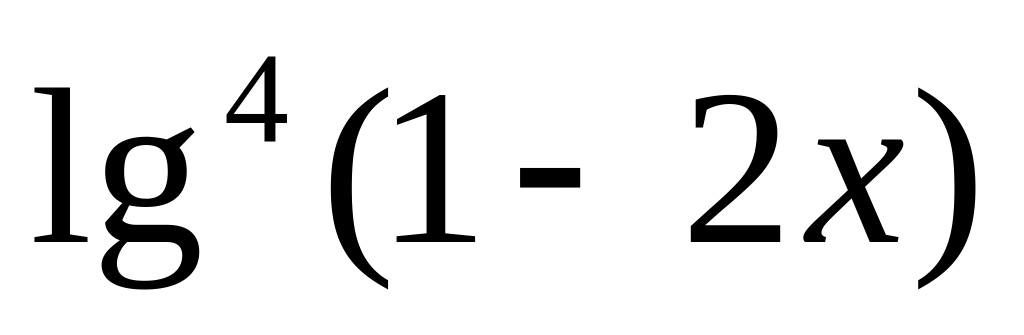
y =
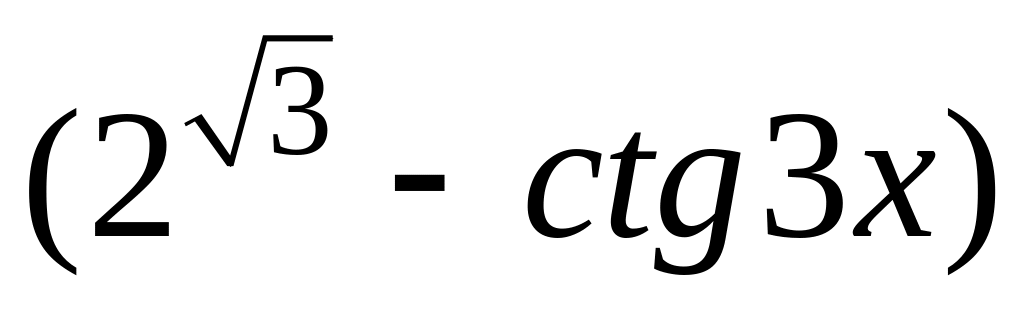 8.
r(
)
=
8.
r(
)
=
S(t) =
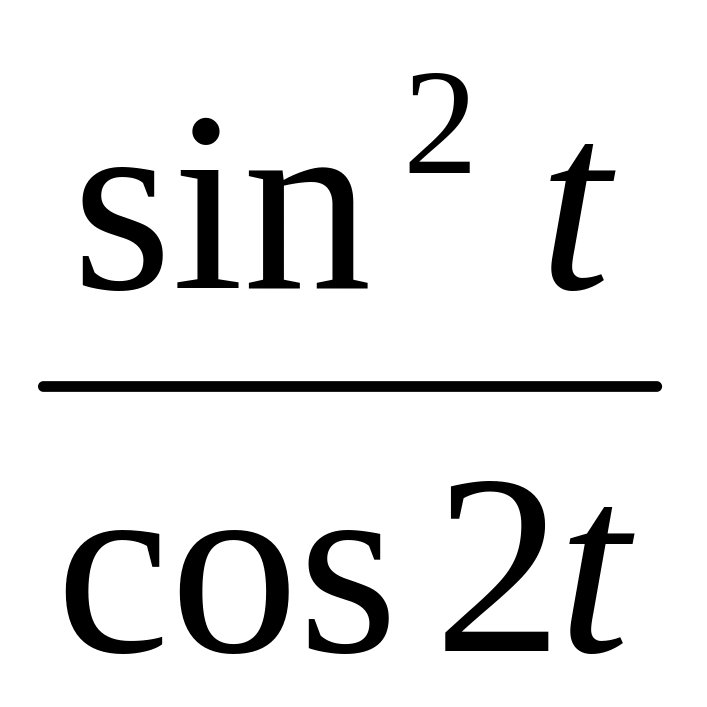 9.
y
=
9.
y
=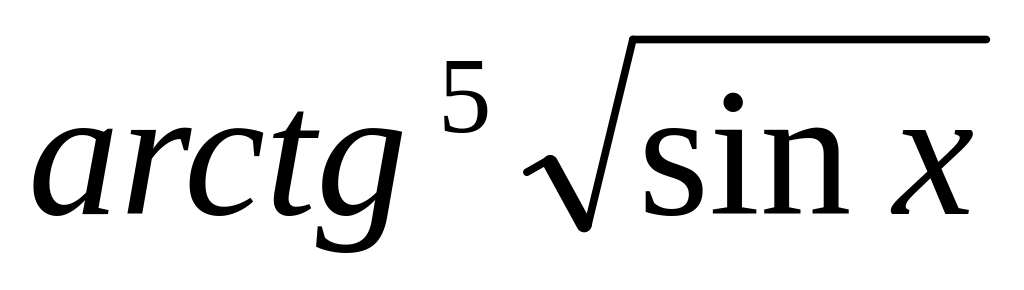
y =
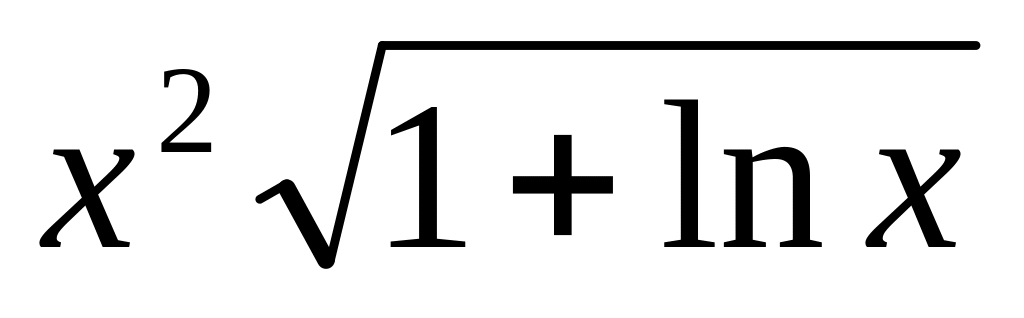 10.
y
=
10.
y
=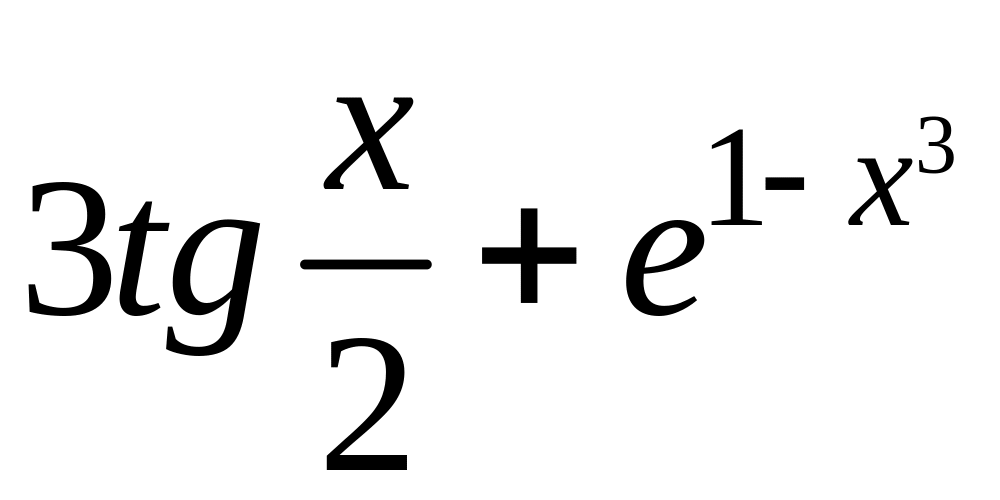
Варіант № 27
y =
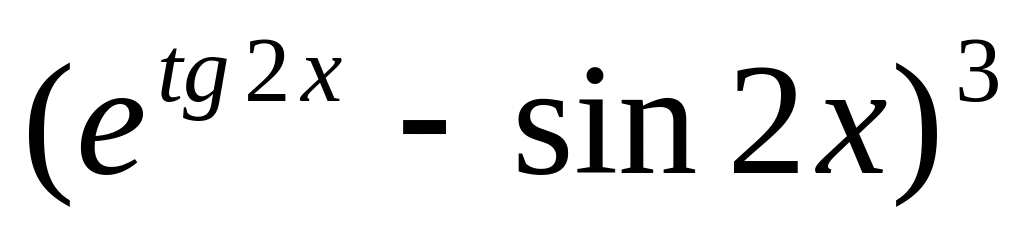 6.
y
=
6.
y
=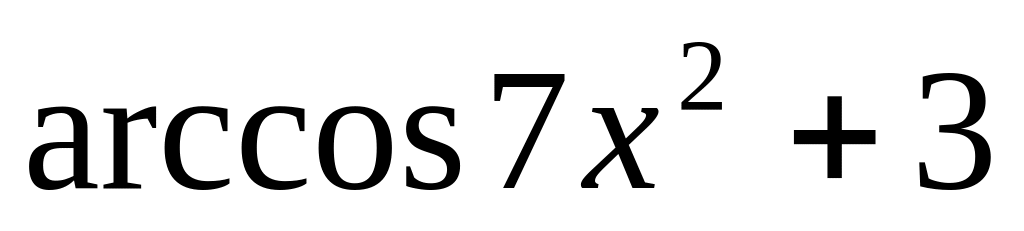
y =
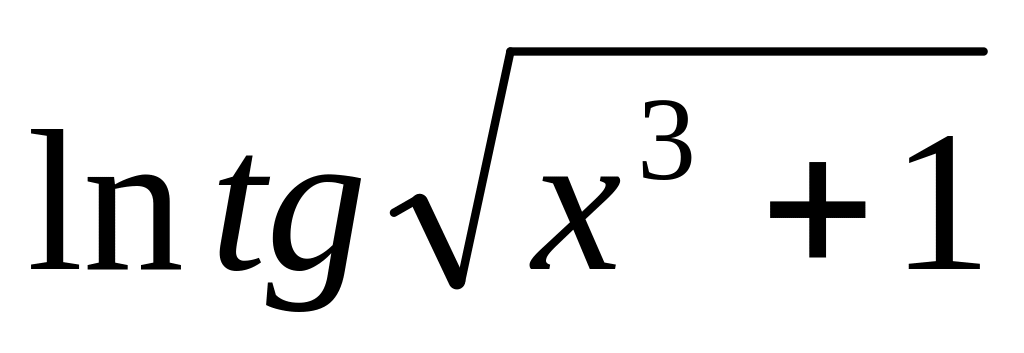 7.
r(
)
=
7.
r(
)
=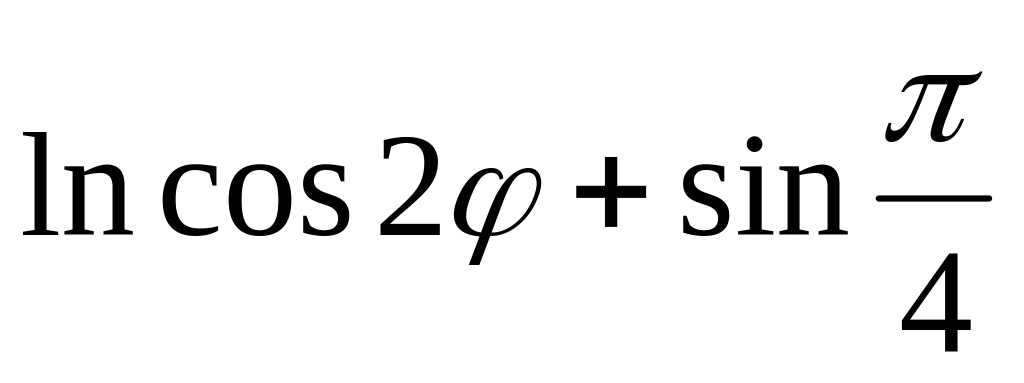
y =
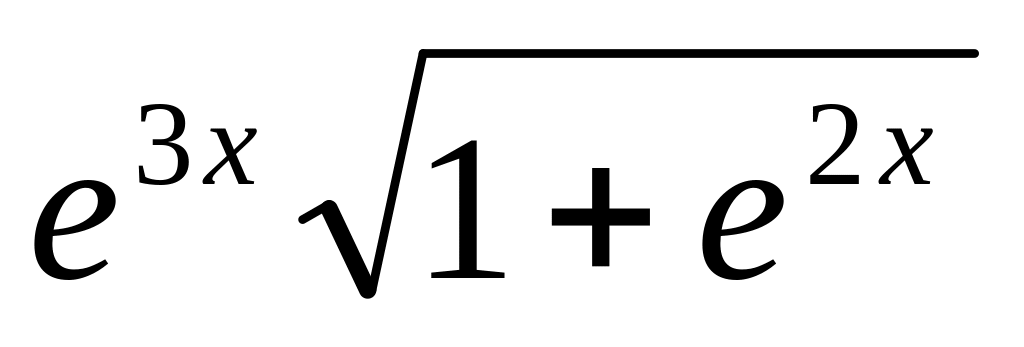 8.
y
=
8.
y
=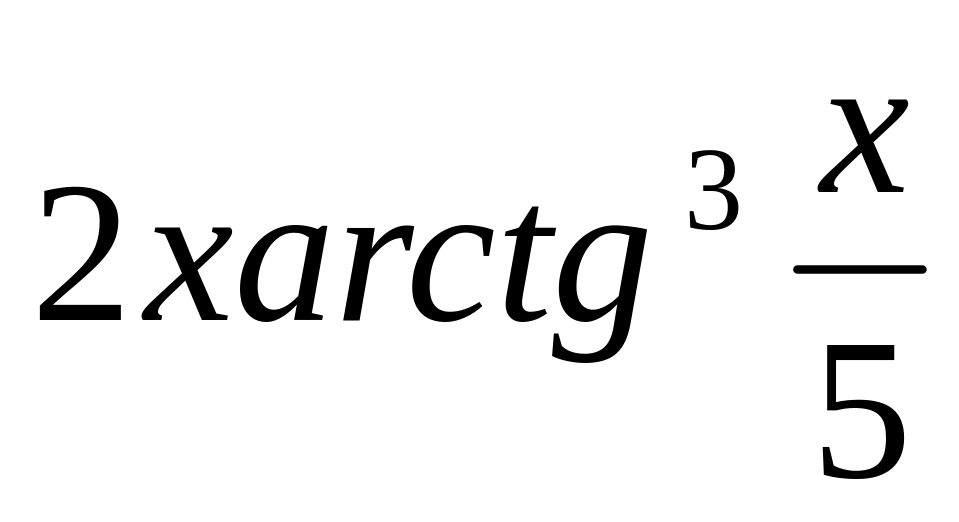
S(t) =
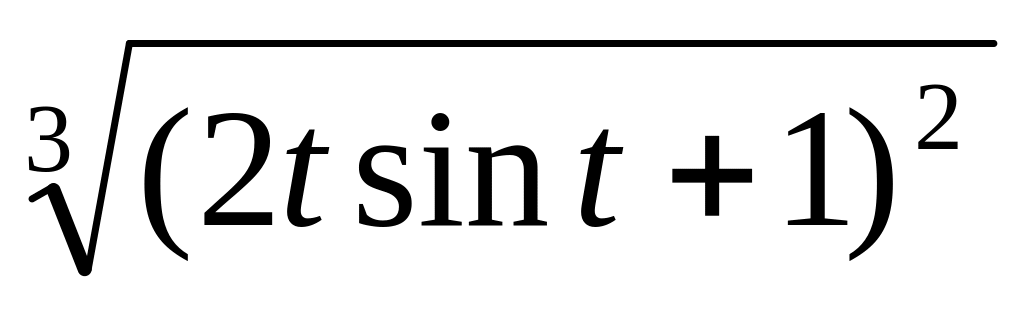 9.
y
=
9.
y
=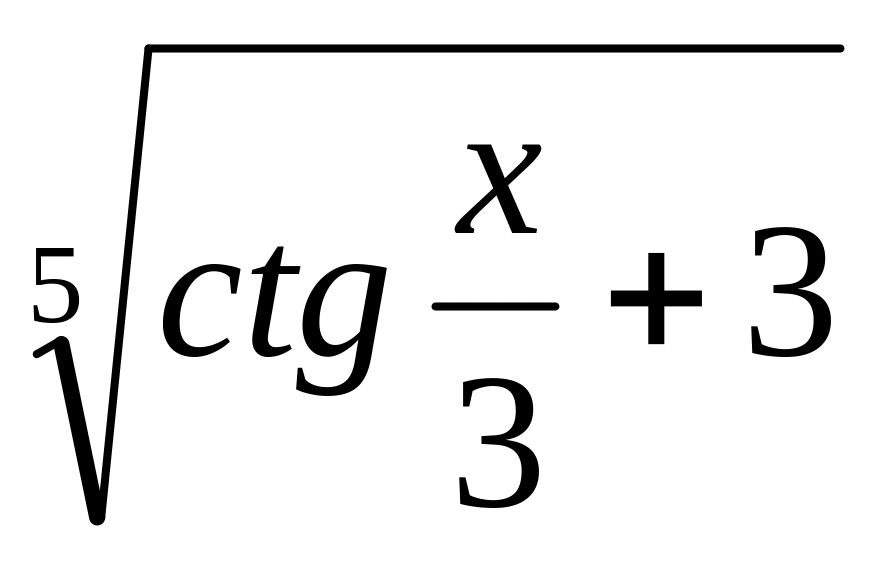
y =
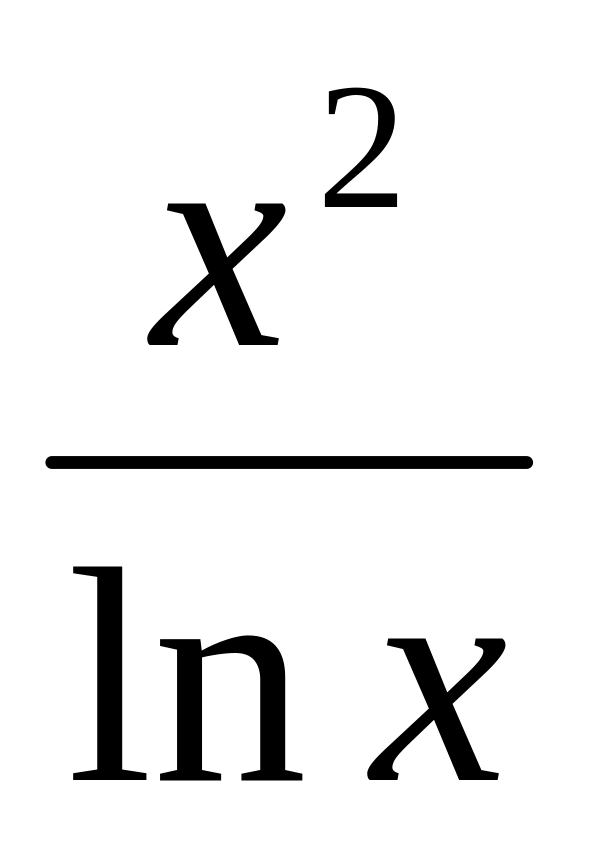 10.
f(t)
=
10.
f(t)
=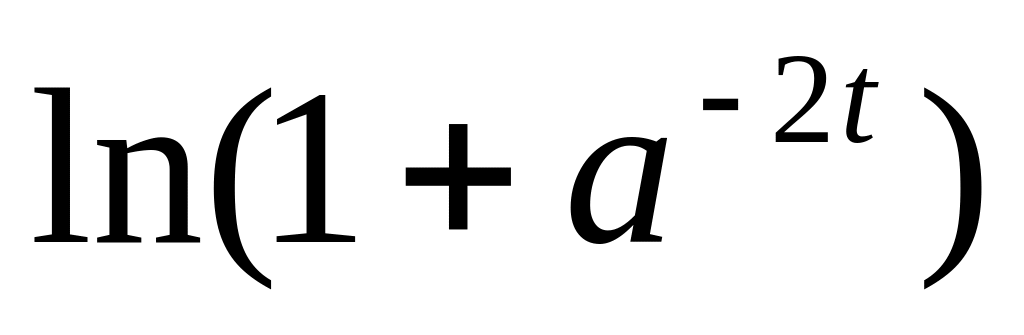
Варіант № 28
y =
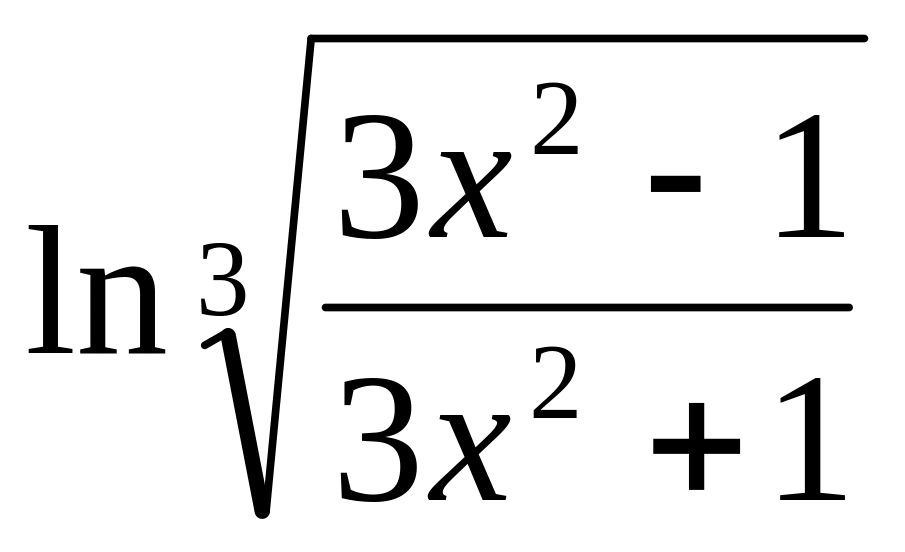 6.
y
=
6.
y
=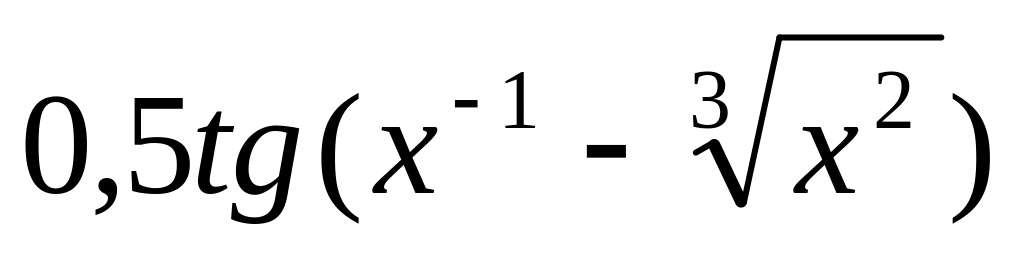
y =
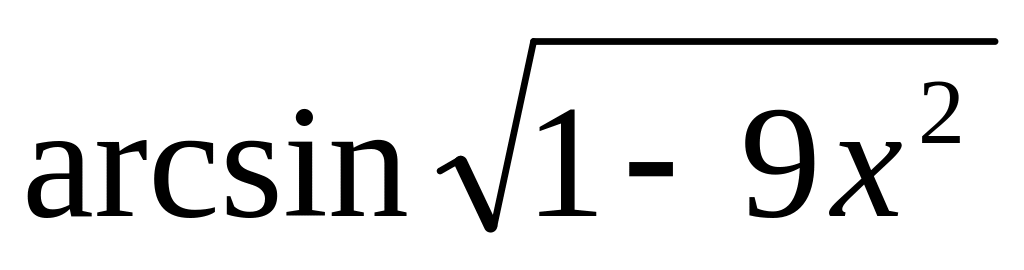 7.
f(t)
=
7.
f(t)
=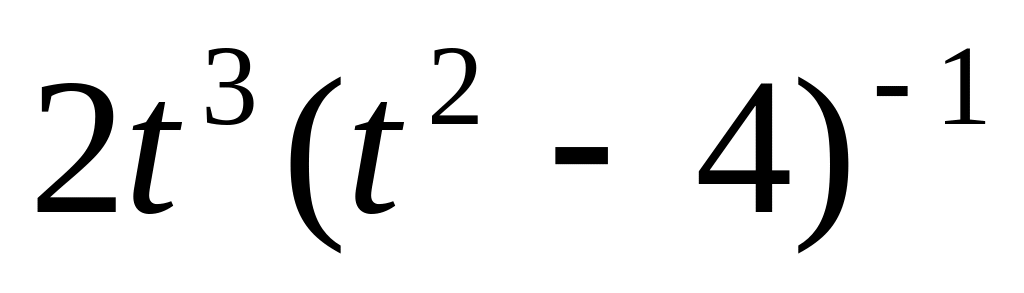
S(t) =
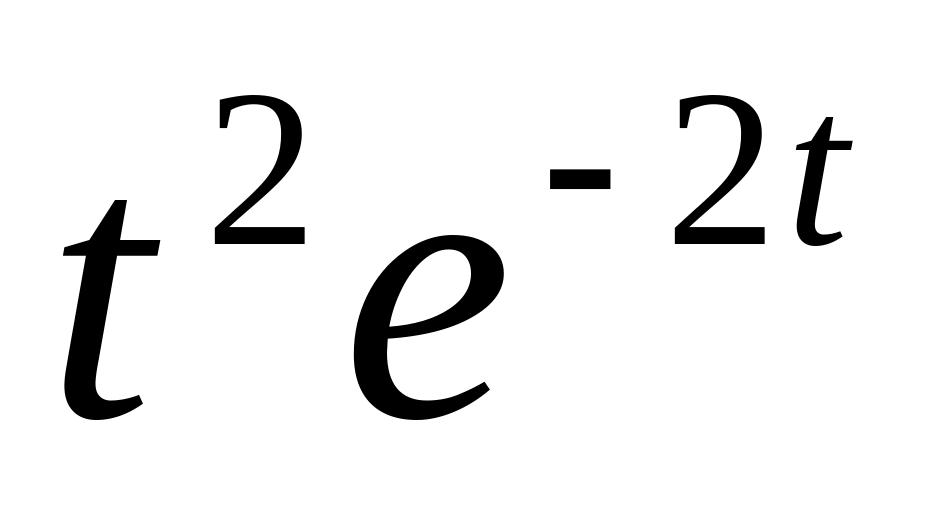 8.
y
=
8.
y
=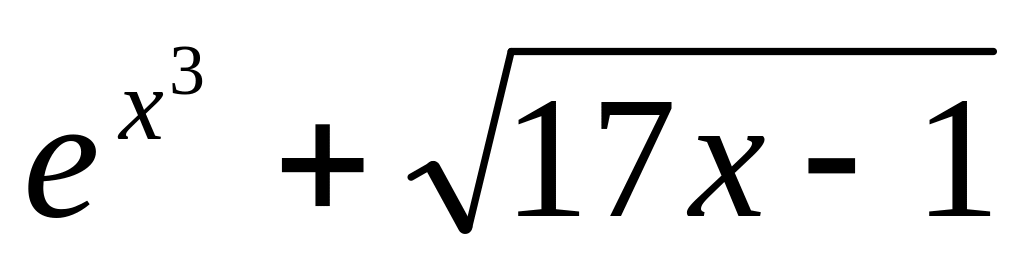
y =
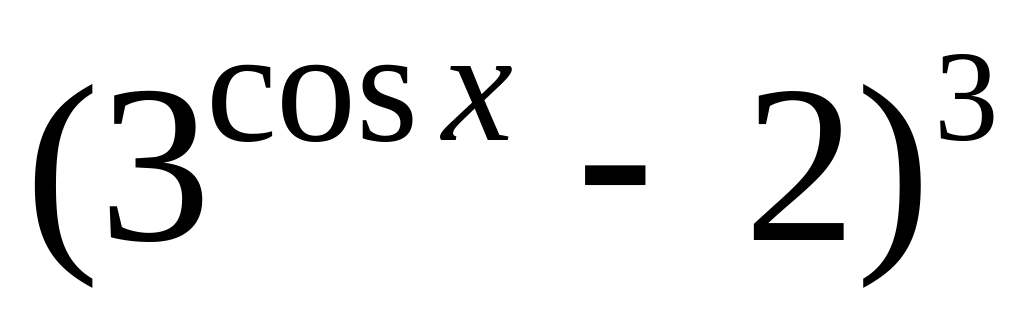 9.
y
=
9.
y
=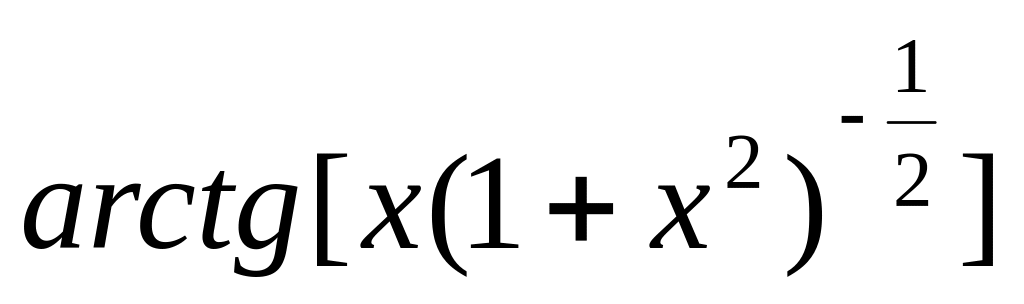
r(
 )
=
)
=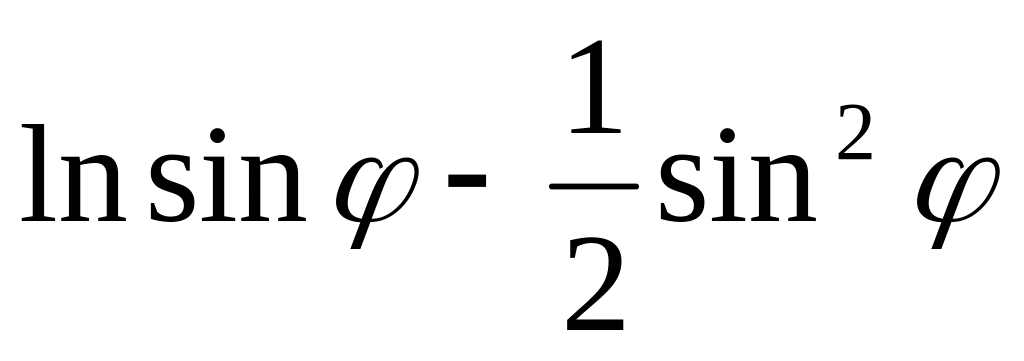 10.
y
=
10.
y
=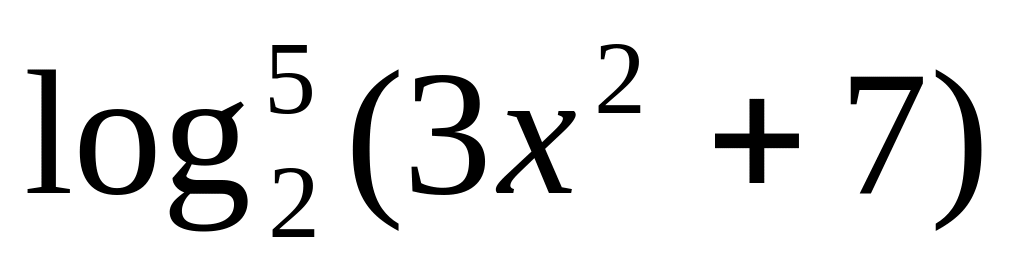
Варіант № 29
y =
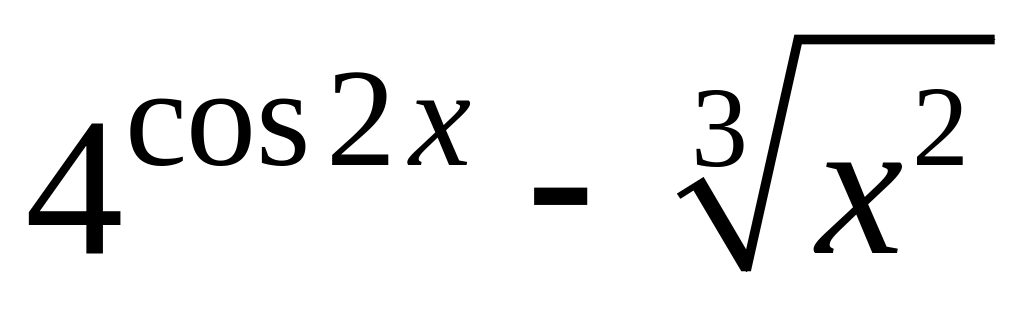 6.
y
=
6.
y
=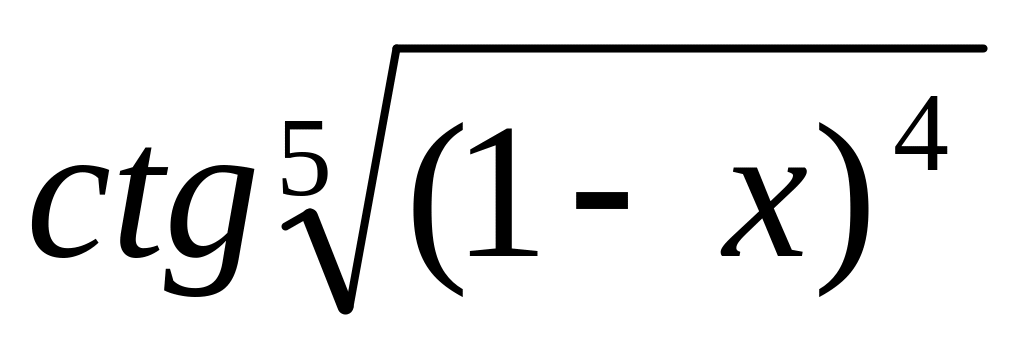
y =
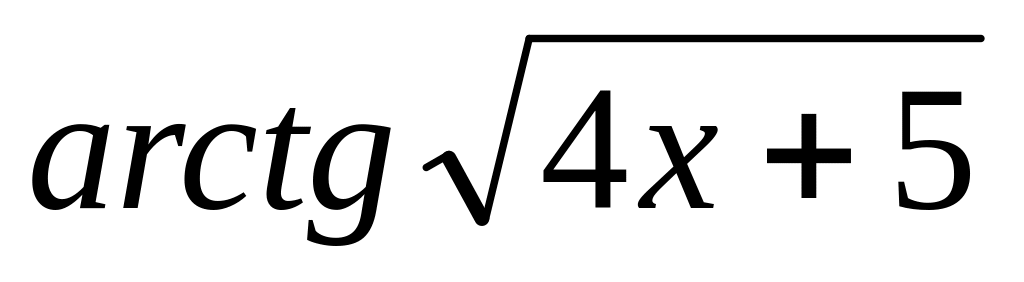 7.
y
=
7.
y
=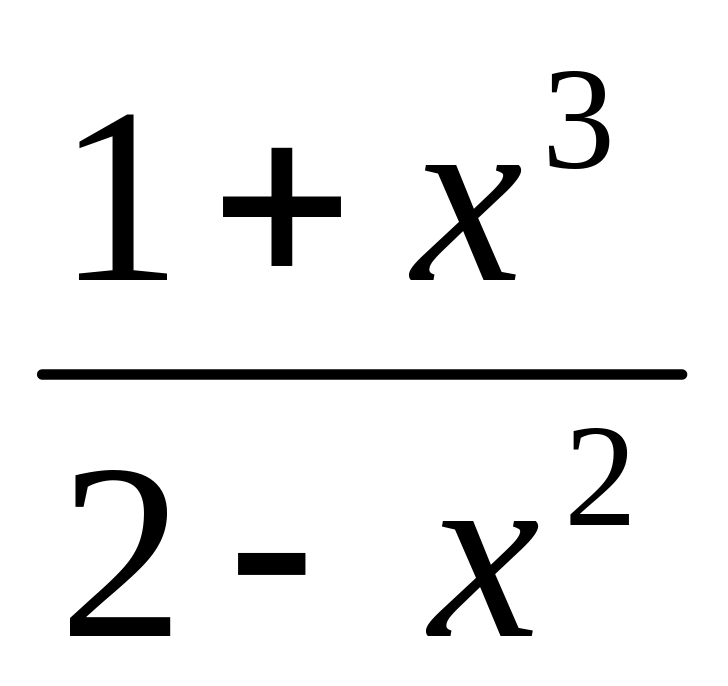
y =
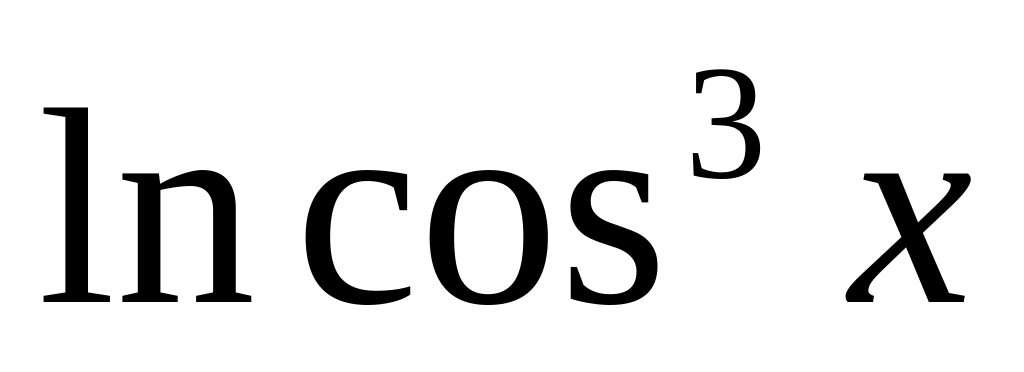 8.
r(
)
=
8.
r(
)
=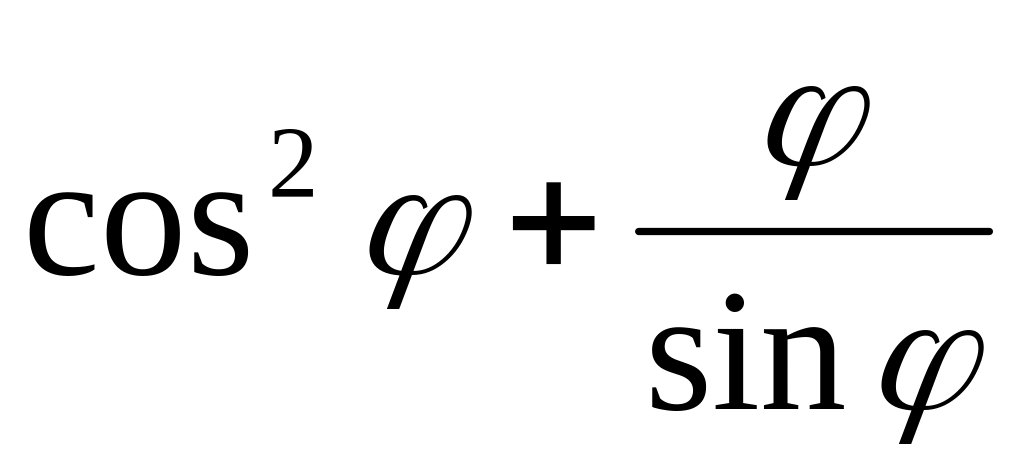
y =
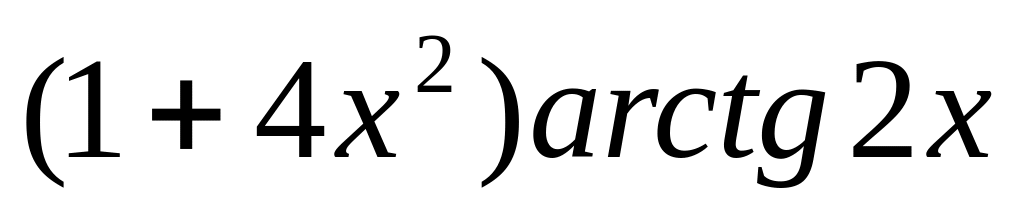 9.
y
=
9.
y
=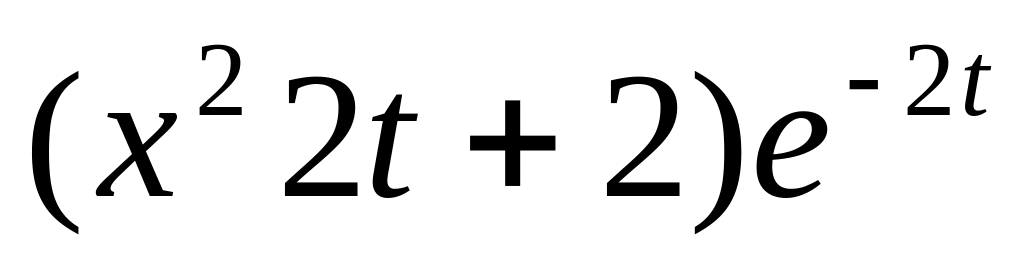
S(t) =
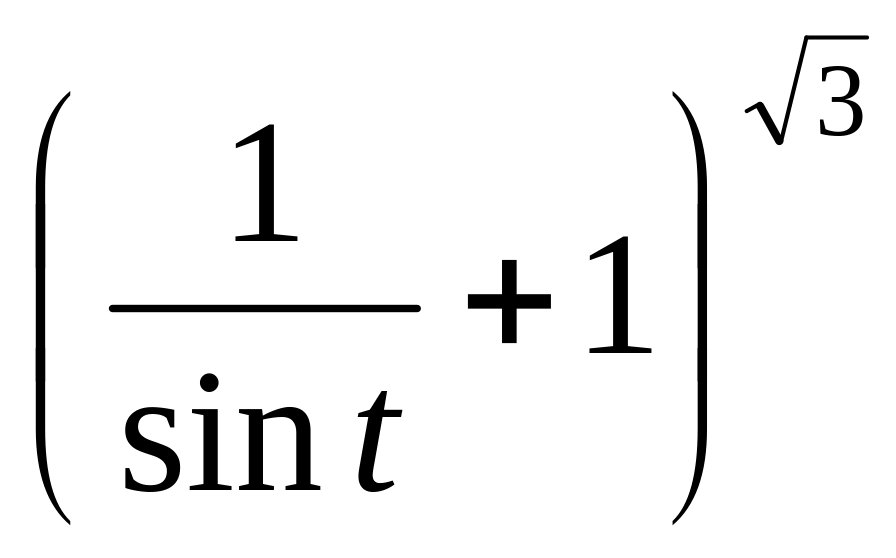 10.
y
=
10.
y
=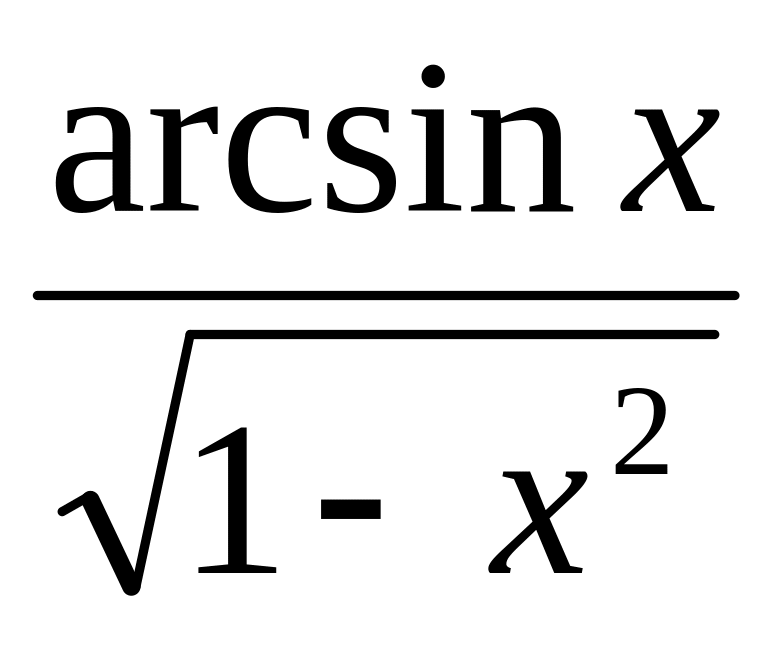
Варіант № 30
y =
 6.
y
=
6.
y
=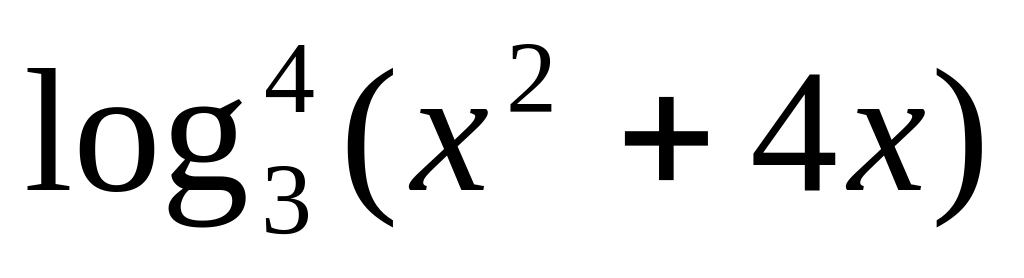
y =
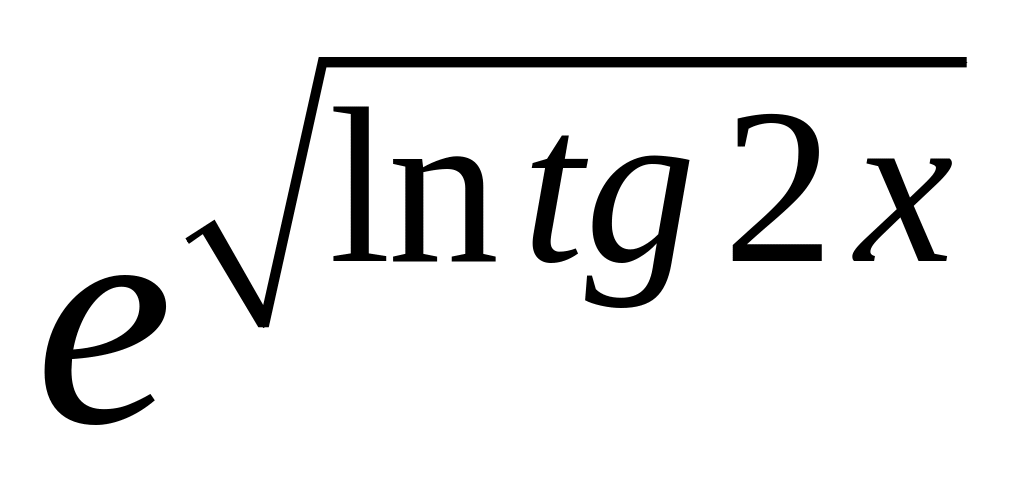 7.
y
=
7.
y
=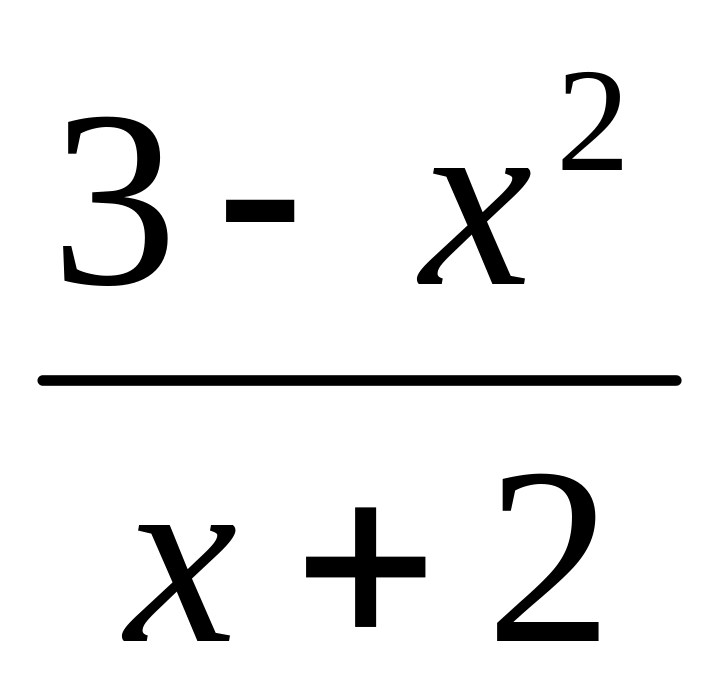
S(t) =
 8.
y
=
8.
y
=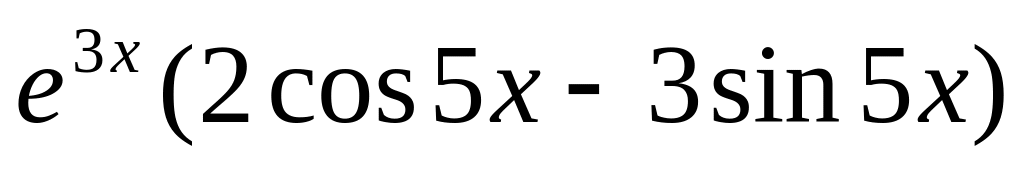
y =
 9.
f(t)
=
9.
f(t)
=
r( ) =
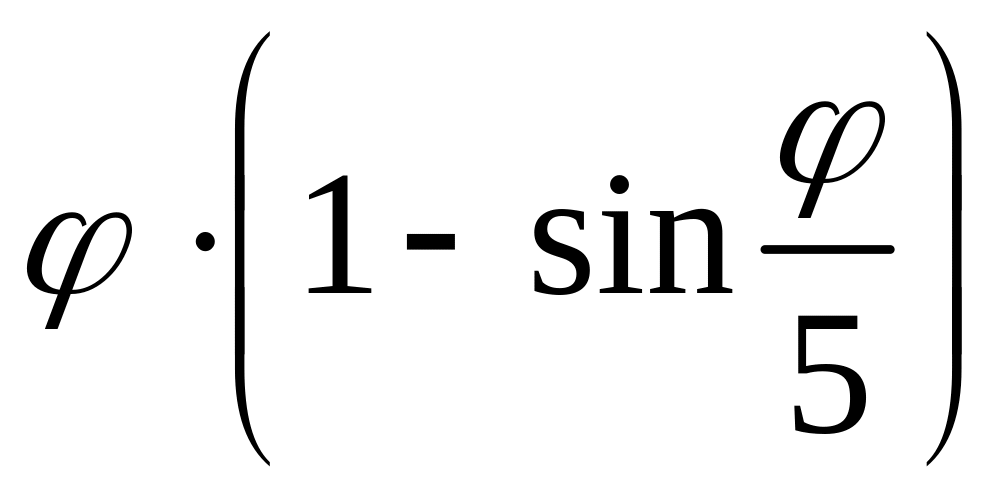 10.
y
=
10.
y
=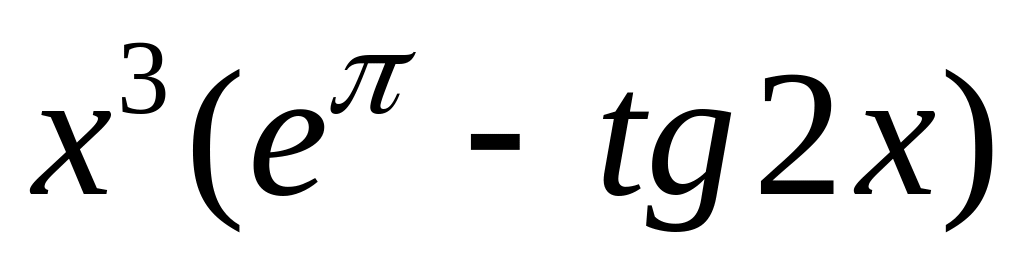
Завдання 5. Знайти похідні першого порядку від заданих функцій.
Варіант № 1
1. y
=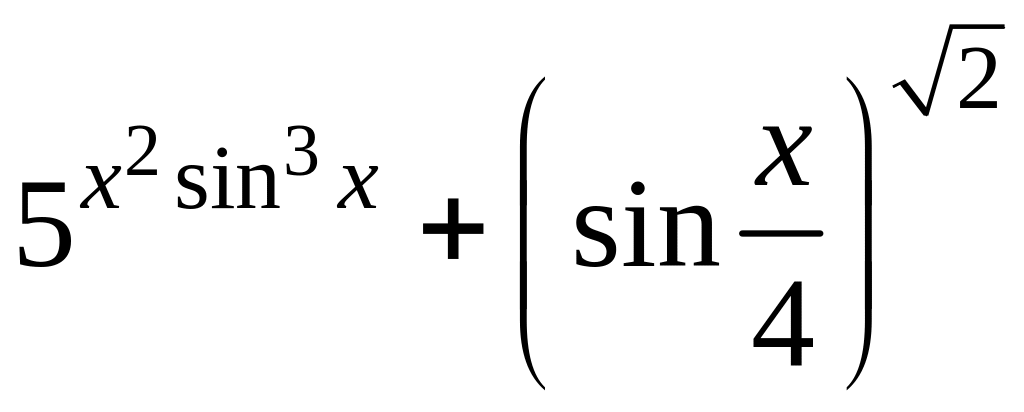 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3.
y=![]() 6.
6.
![]()
Варіант № 2
1. y
=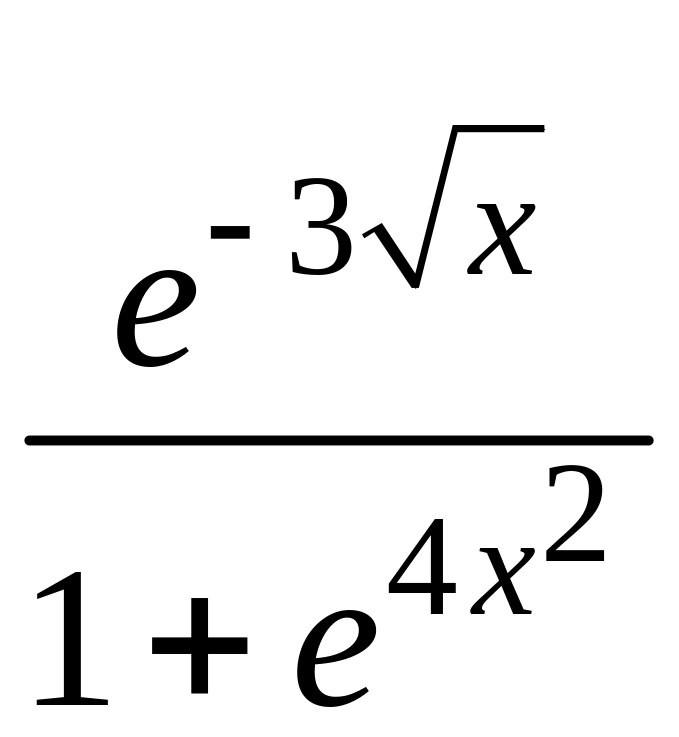 4.
y
=
4.
y
=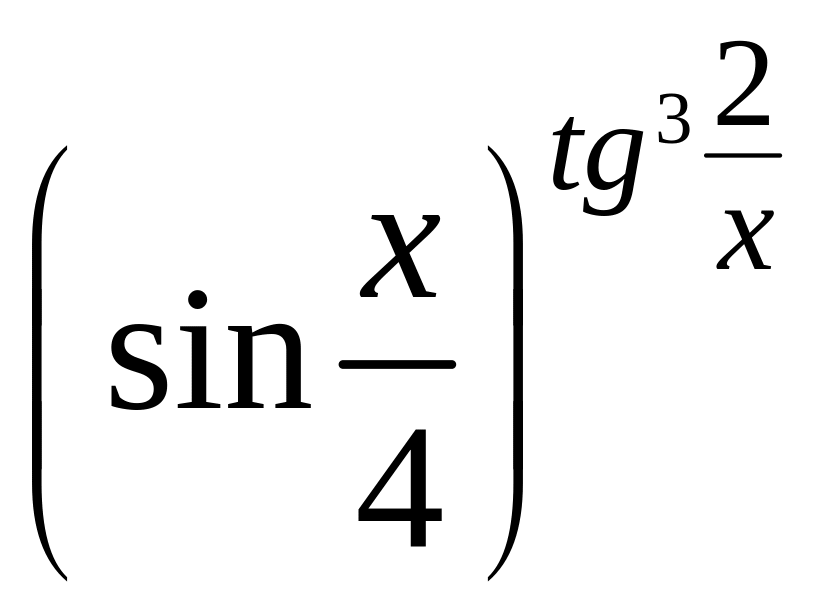
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 3
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 4
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 5
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=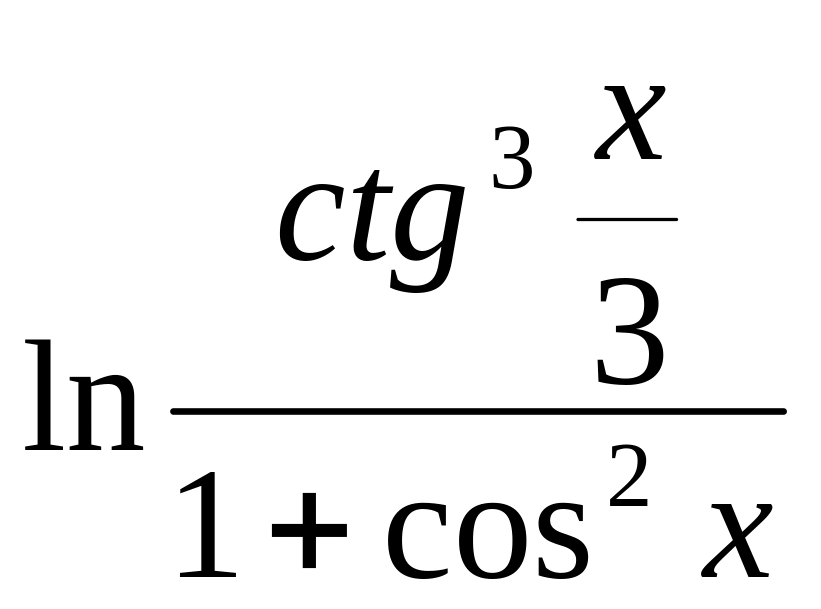 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 6
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 7
1.y
=![]() 4.y
=
4.y
=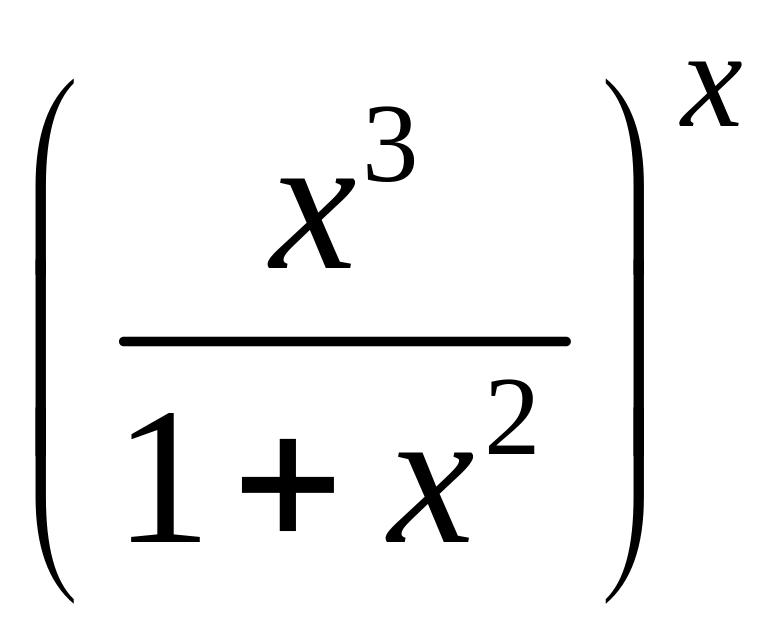
2.y
=![]() 5.
5.![]()
3.y
=![]() 6.
6.![]()
Варіант № 8
1. y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 9
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=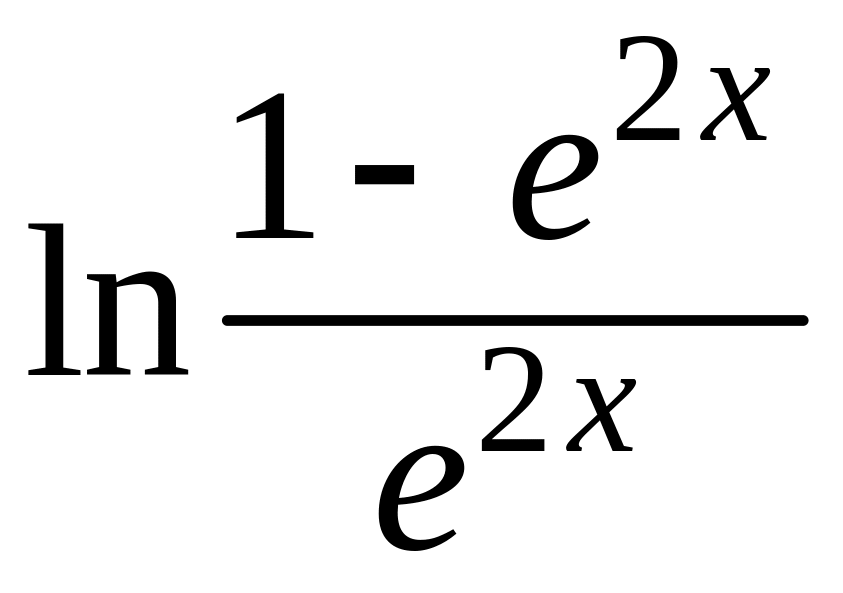 6.
6.
![]()
Варіант № 10
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=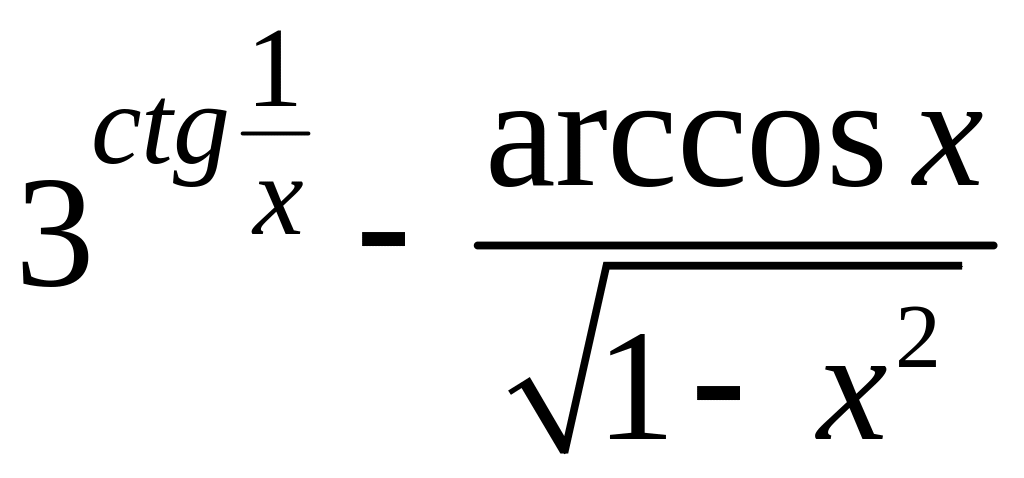 6.
6.
![]()
Варіант № 11
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=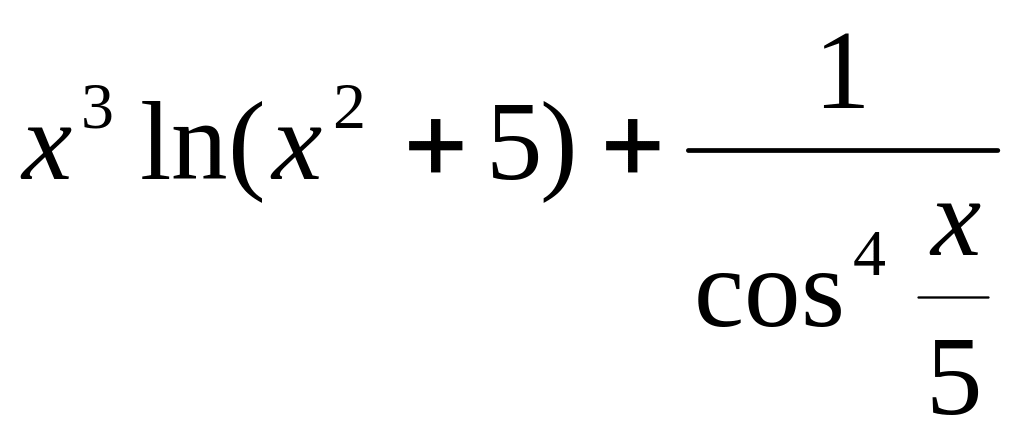 6.
6.
![]()
Варіант № 12
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=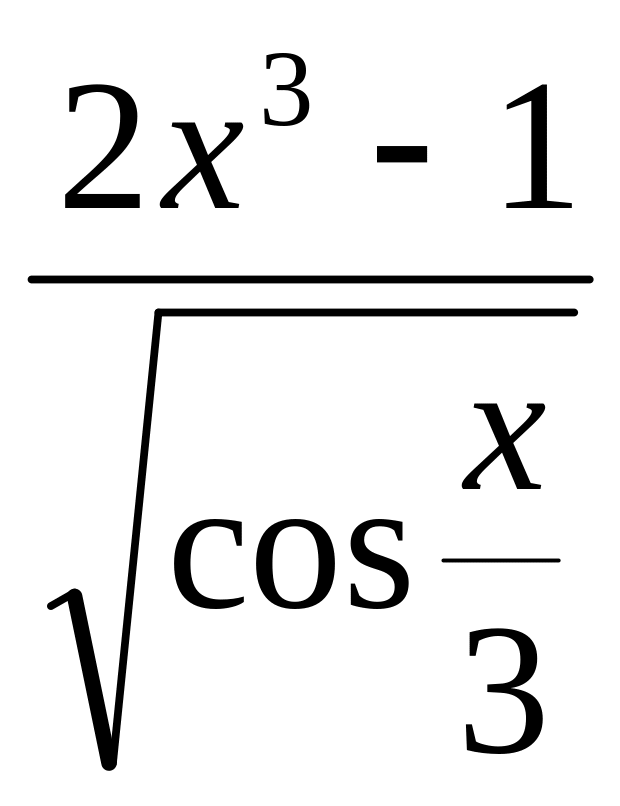 6.
6.
![]()
Варіант № 13
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=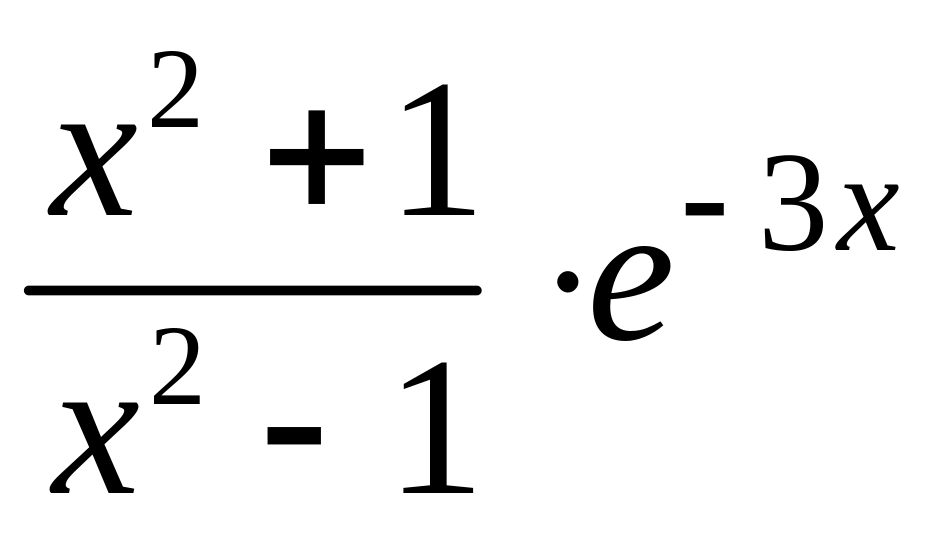 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 14
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 15
1. y
=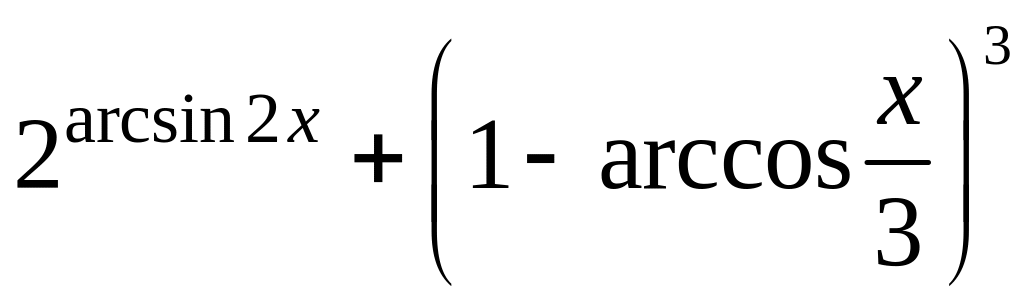 4.
y
=
4.
y
=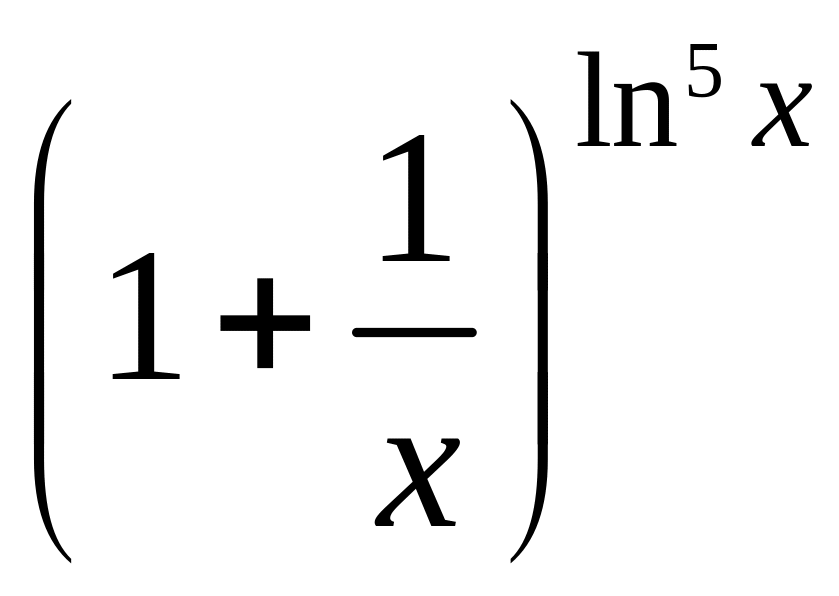
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 16
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 17
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=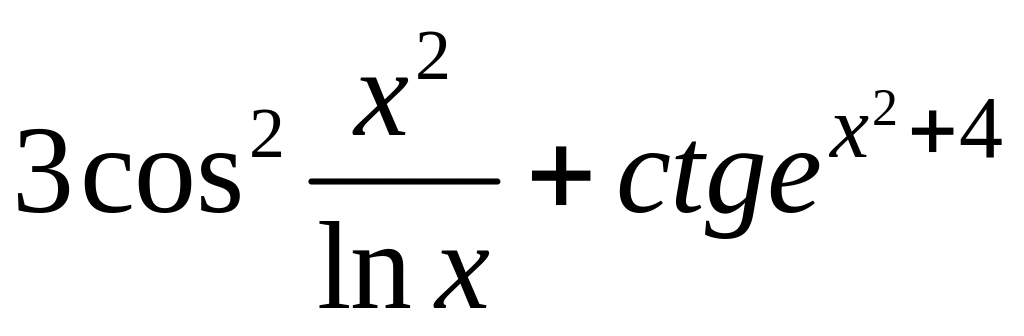 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 18
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 19
1. y
=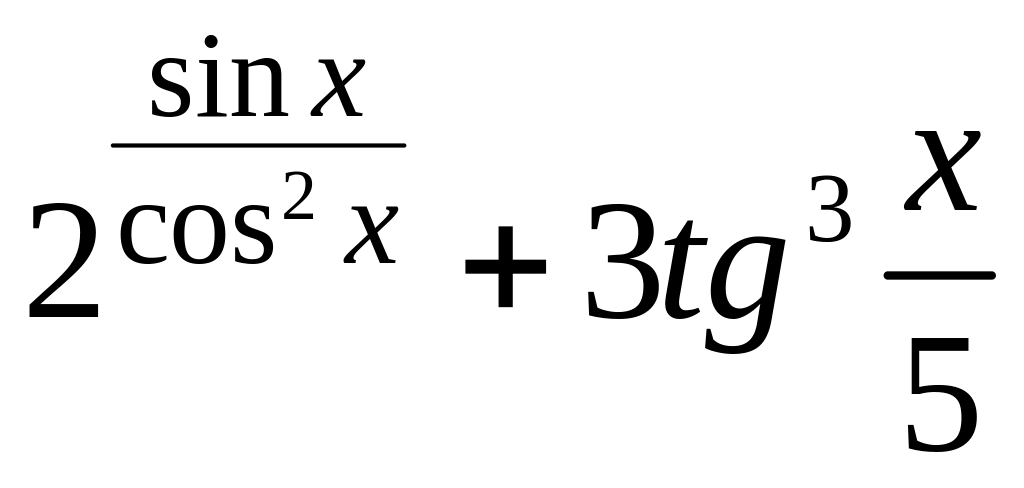 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 20
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 21
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=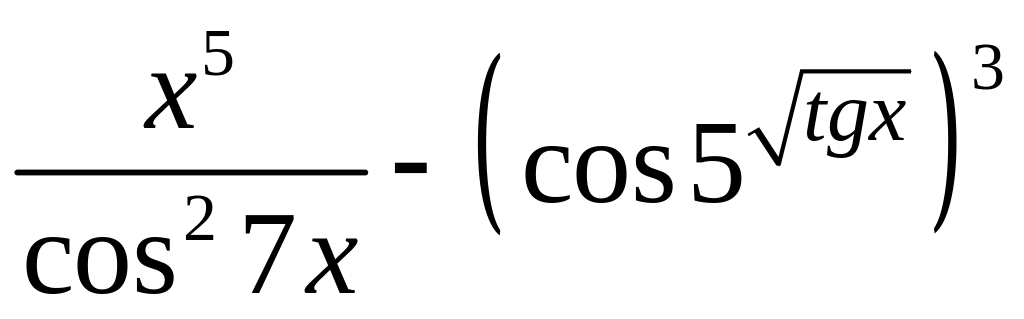 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 22
1. y
=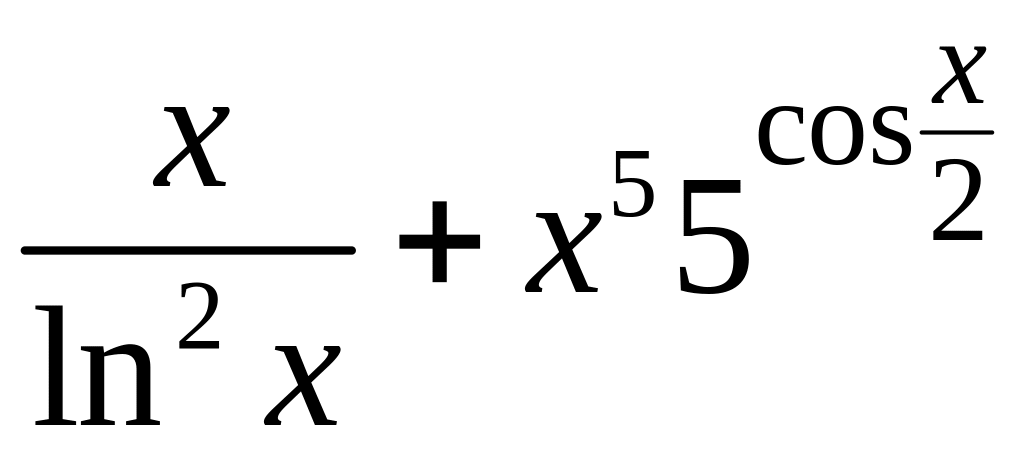 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 23
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 24
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=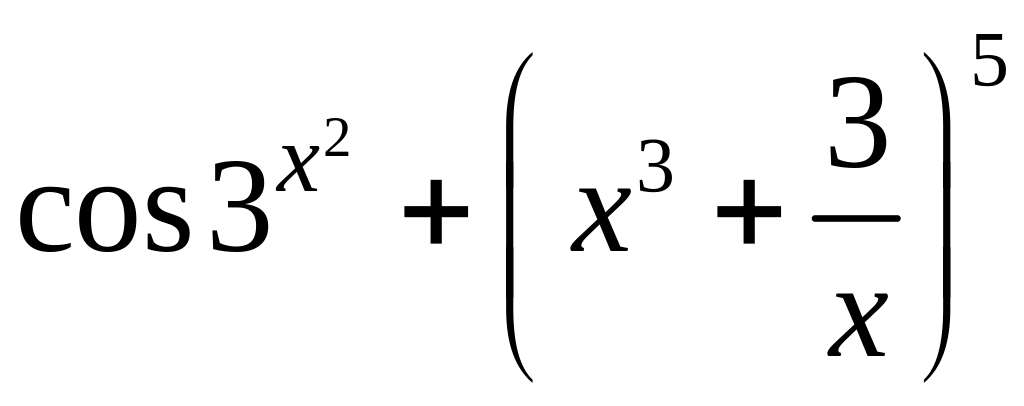 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 25
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=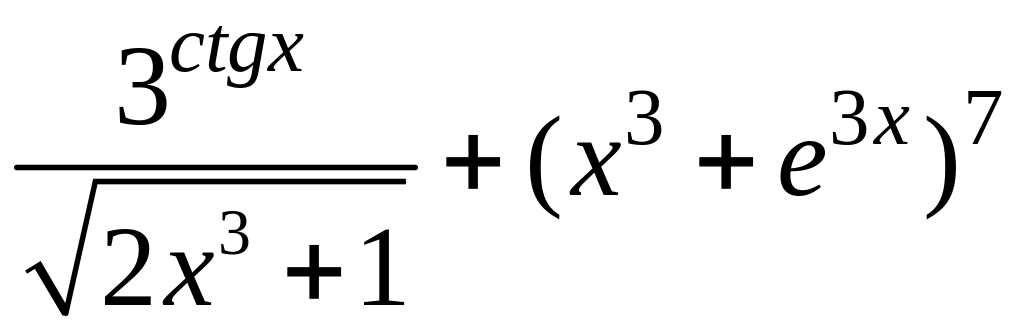 6.
6.
![]()
Варіант № 26
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 27
1.y
=![]() 4.
y
=
4.
y
=![]()
2.y
=![]() 5.
5.
![]()
3.y
=![]() 6.
6.
![]()
Варіант № 28
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 29
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Варіант № 30
1. y
=![]() 4.
y
=
4.
y
=![]()
2. y
=![]() 5.
5.
![]()
3. y
=![]() 6.
6.
![]()
Завдання 6. Знайти похідні другого порядку від заданих функцій.
Варіант № 1 Варіант № 2
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.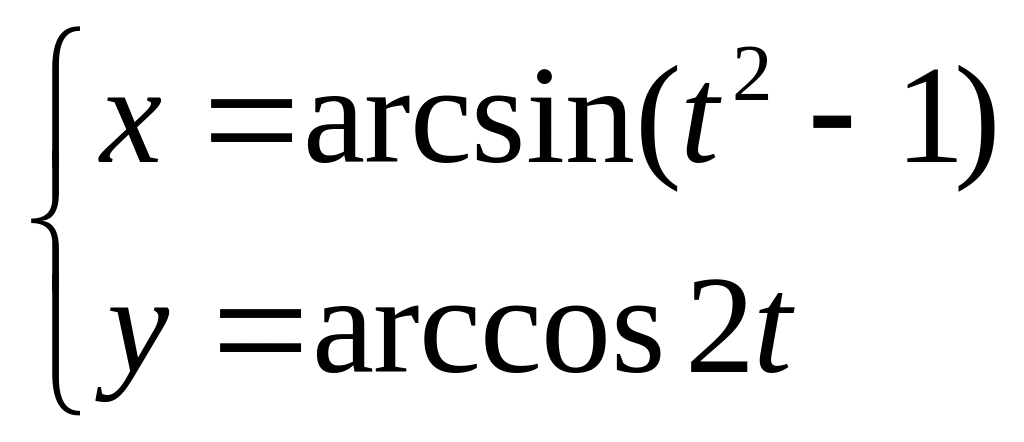 3.
3.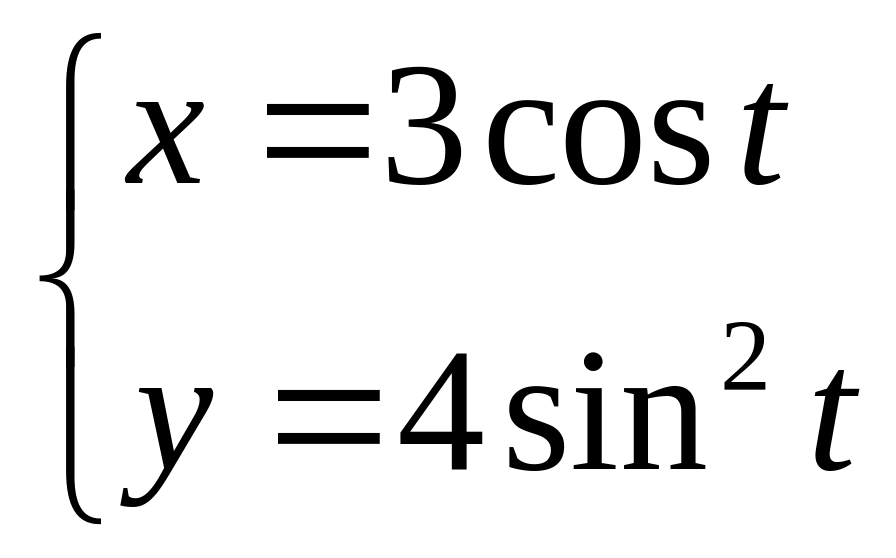
Варіант № 3 Варіант № 4
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.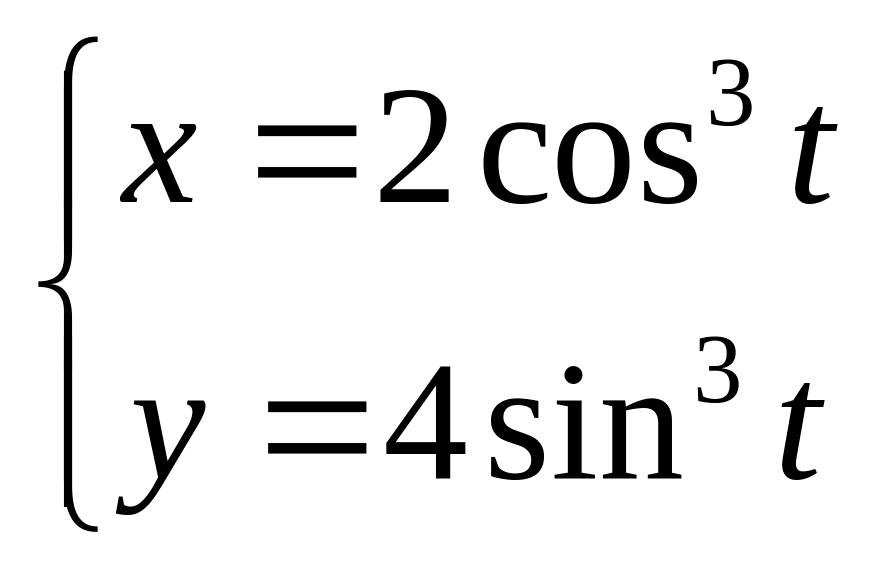 3.
3.![]()
Варіант № 5 Варіант № 6
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.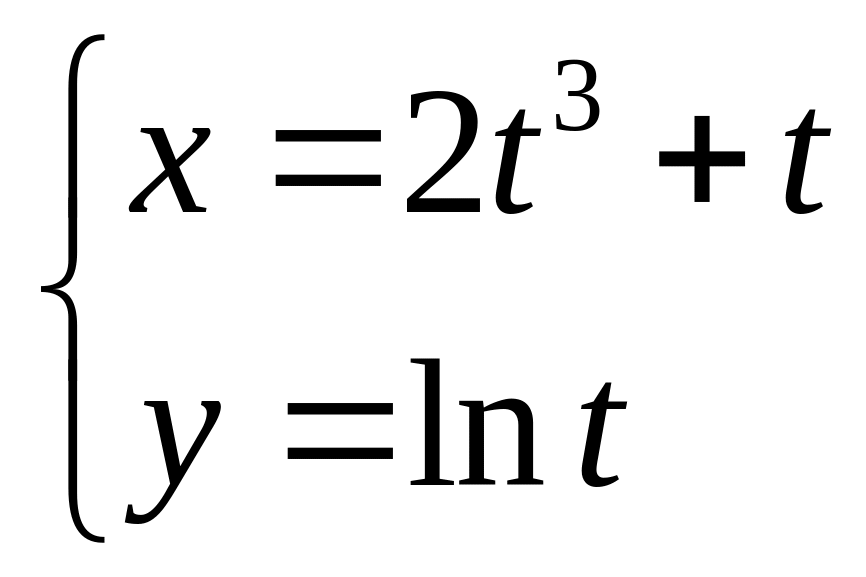 3.
3.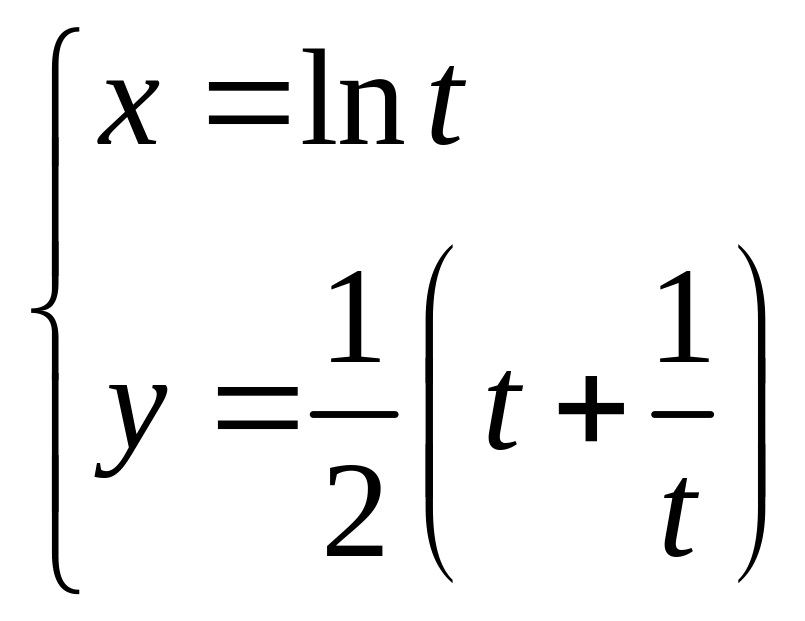
Варіант № 7 Варіант № 8
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.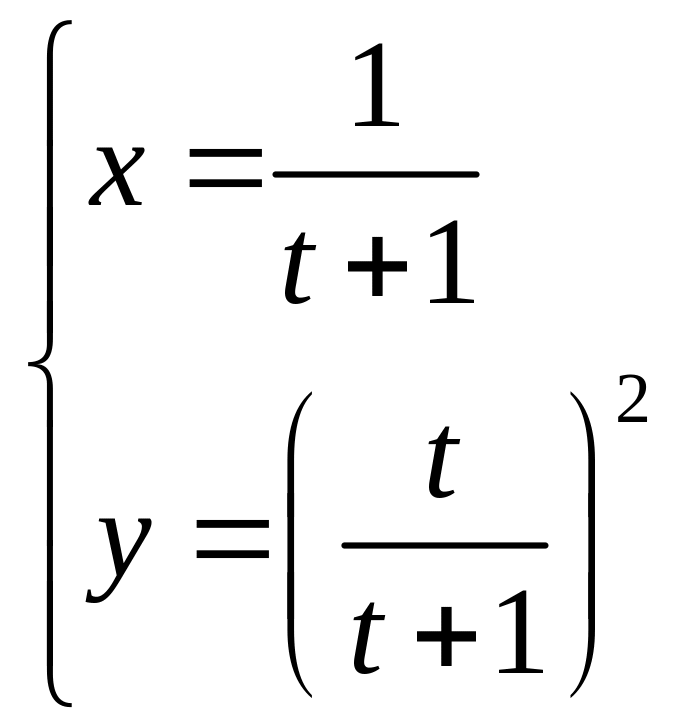 3.
3.![]()
Варіант № 9 Варіант № 10
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.![]() 3.
3.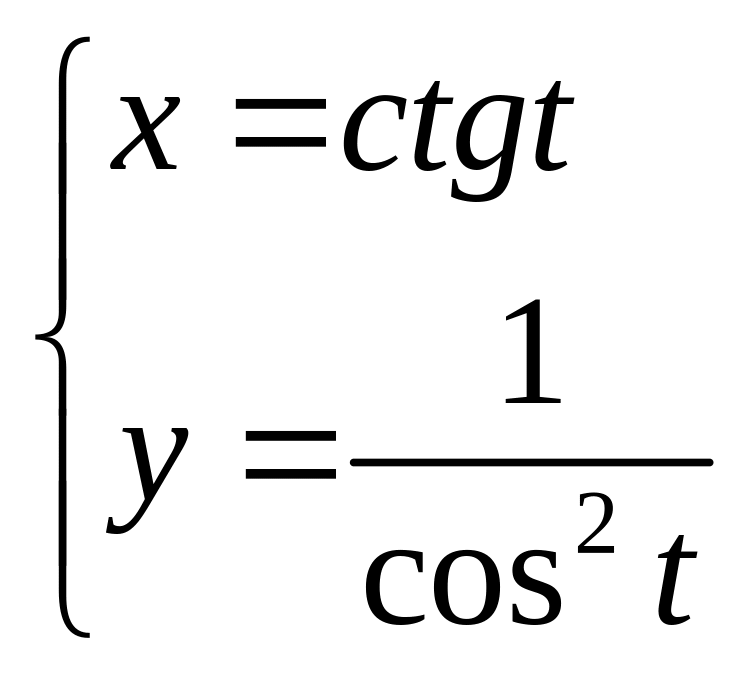
Варіант № 11 Варіант № 12
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.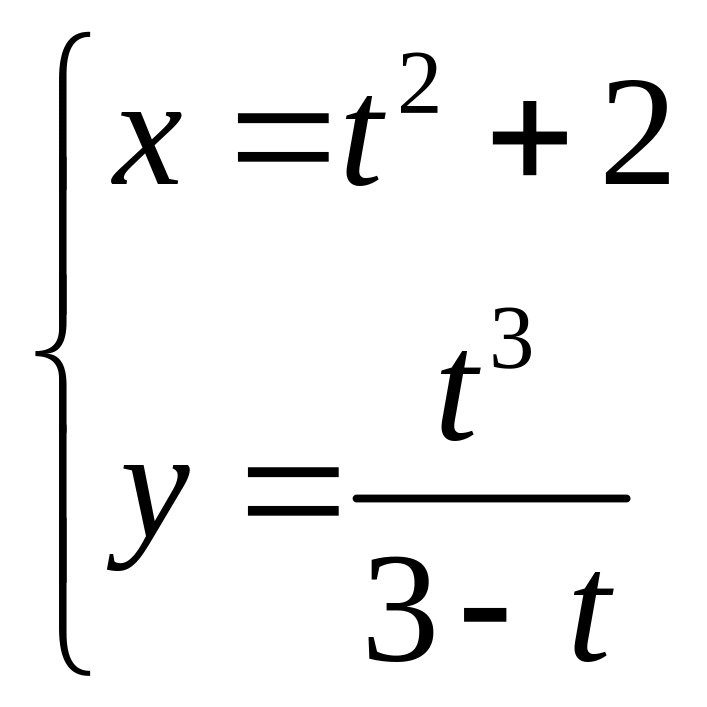 3.
3.![]()
Варіант № 13 Варіант № 14
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.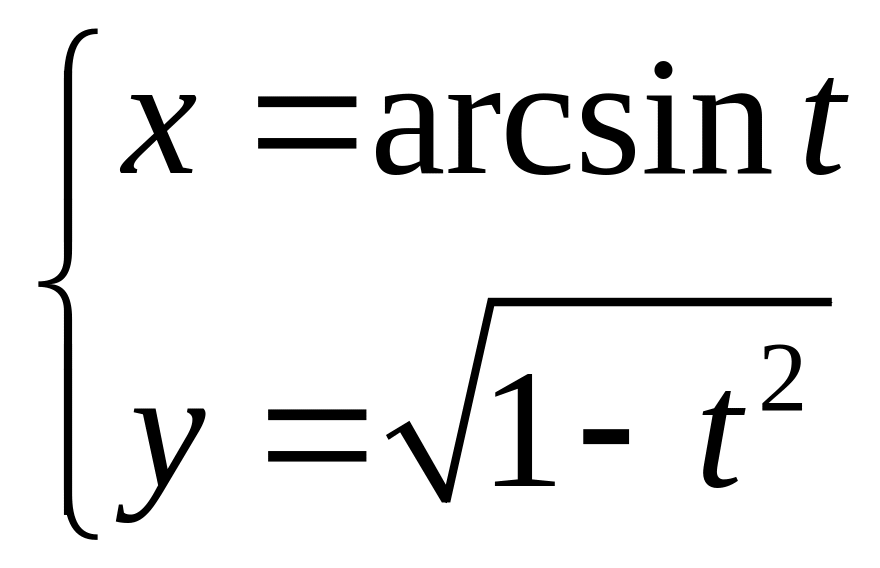 3.
3.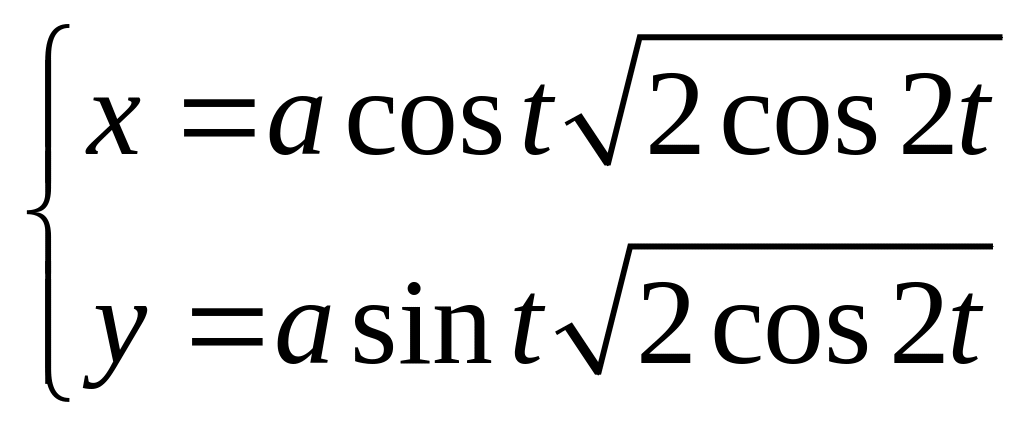
Варіант № 15 Варіант № 16
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.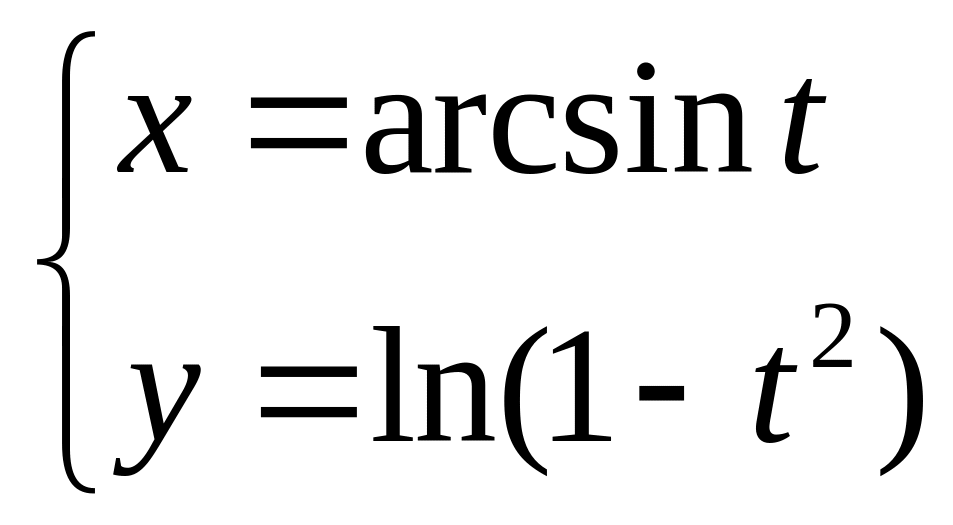 3.
3.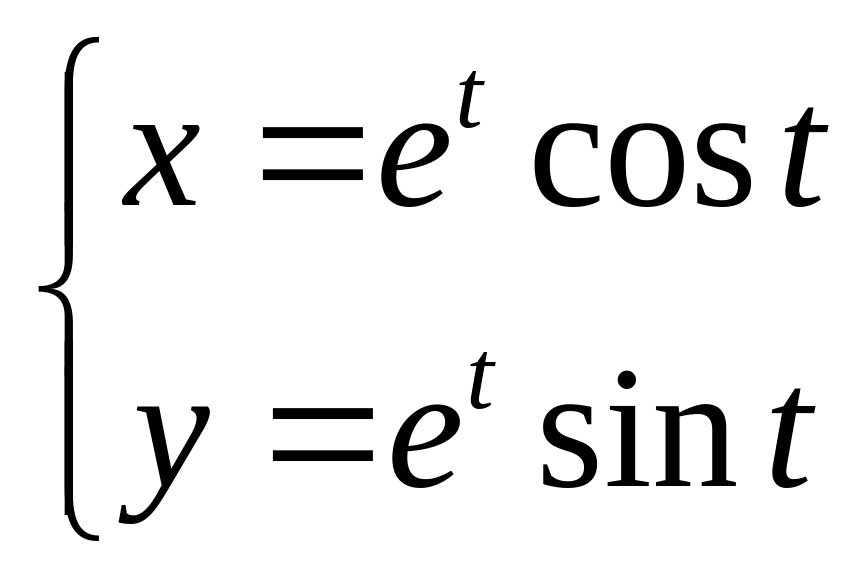
Варіант № 17 Варіант № 18
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.![]() 3 .
3 .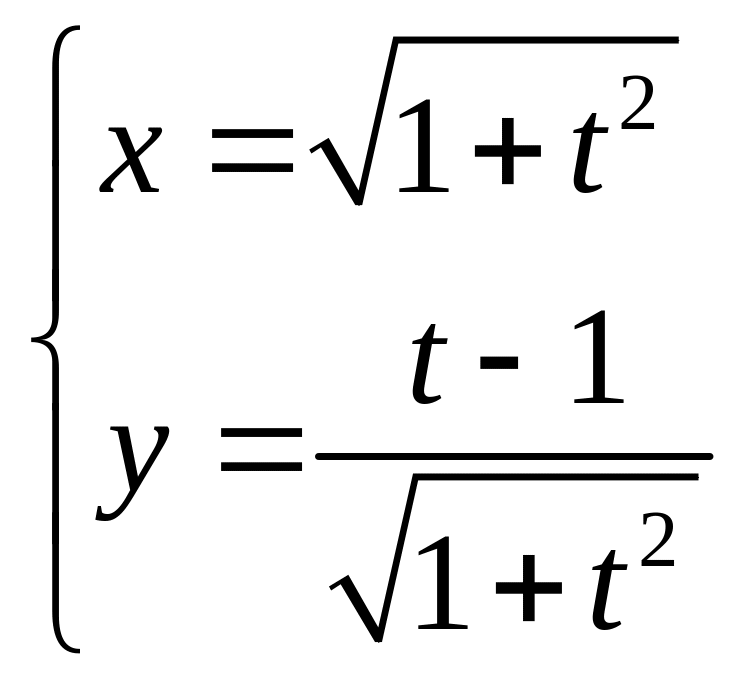
Варіант № 19 Варіант № 20
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.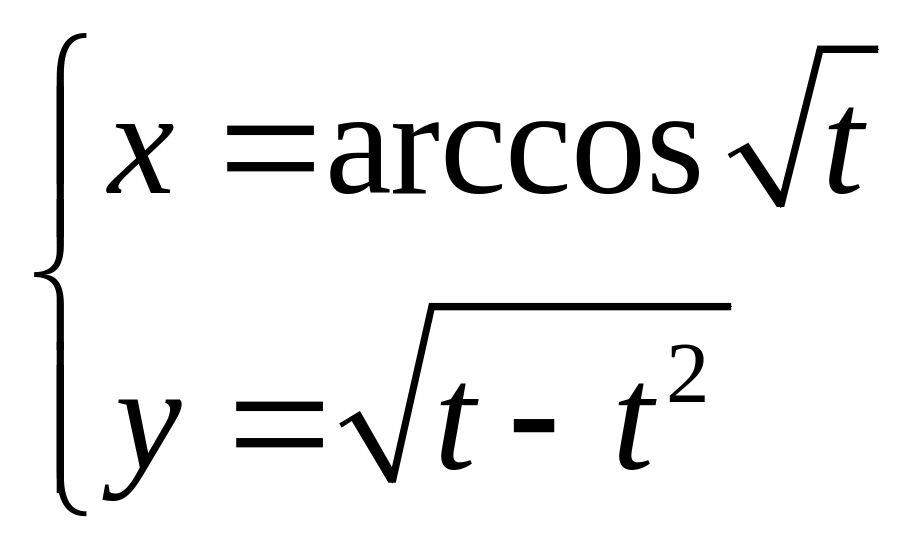 3.
3.
Варіант № 21 Варіант № 22
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3. 3.
3.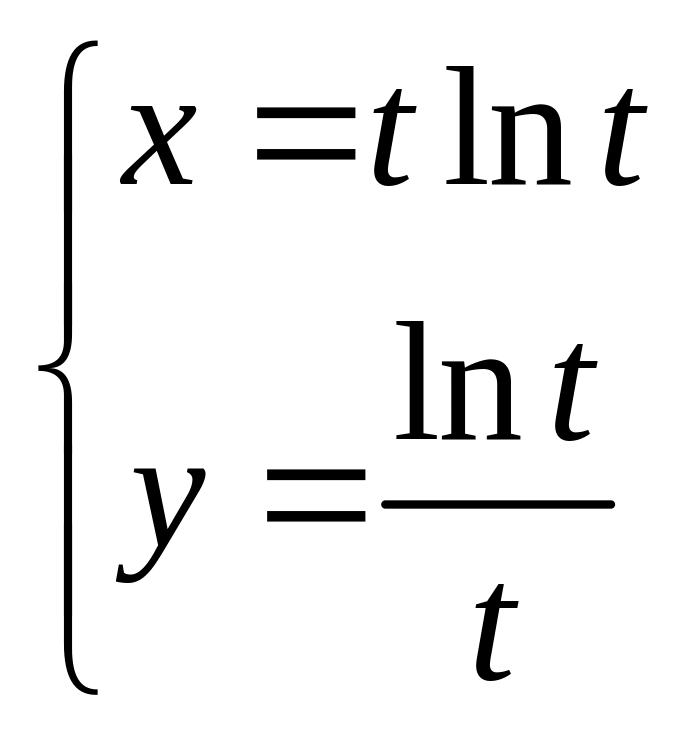
Варіант № 23 Варіант № 24
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3. 3.
3.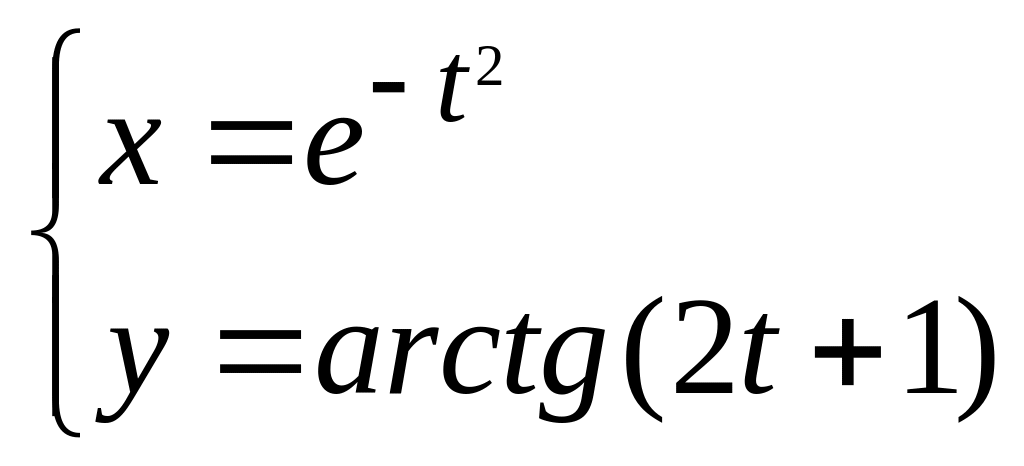
Варіант № 25 Варіант № 26
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.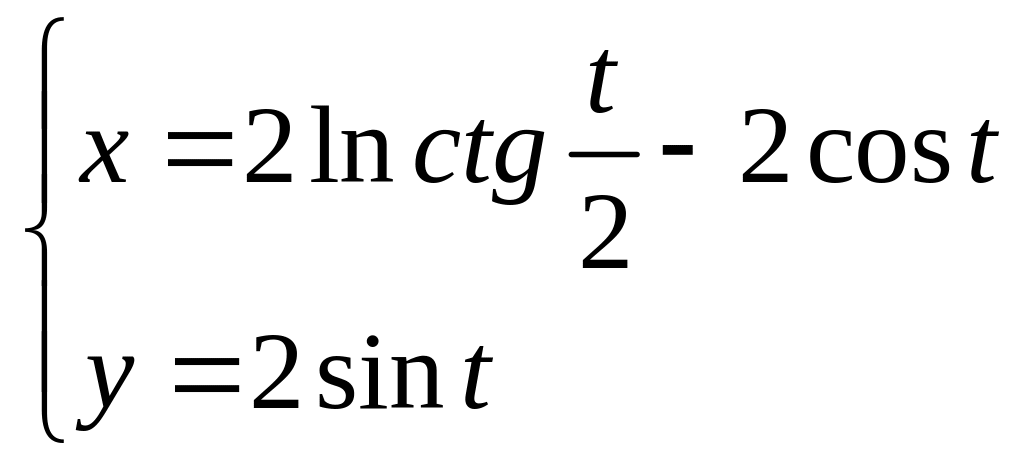 3.
3.
Варіант № 27 Варіант № 28
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.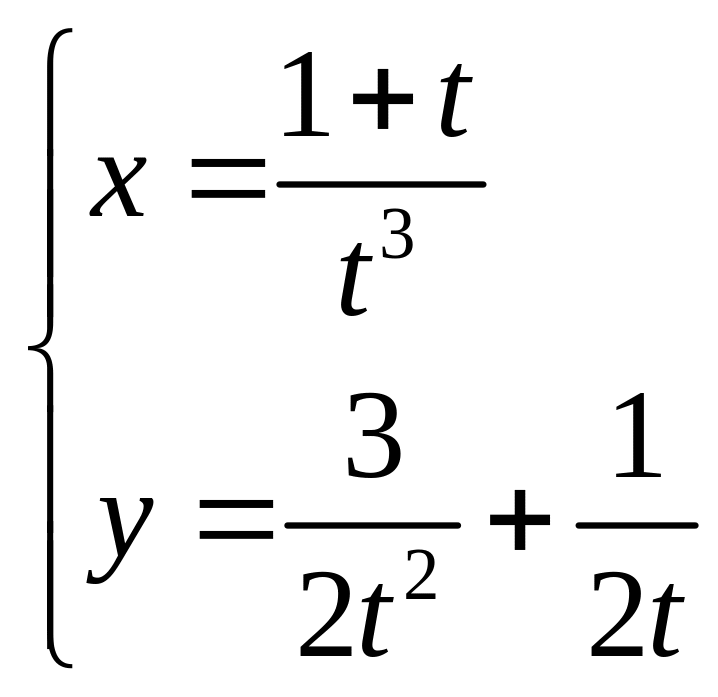 3.
3.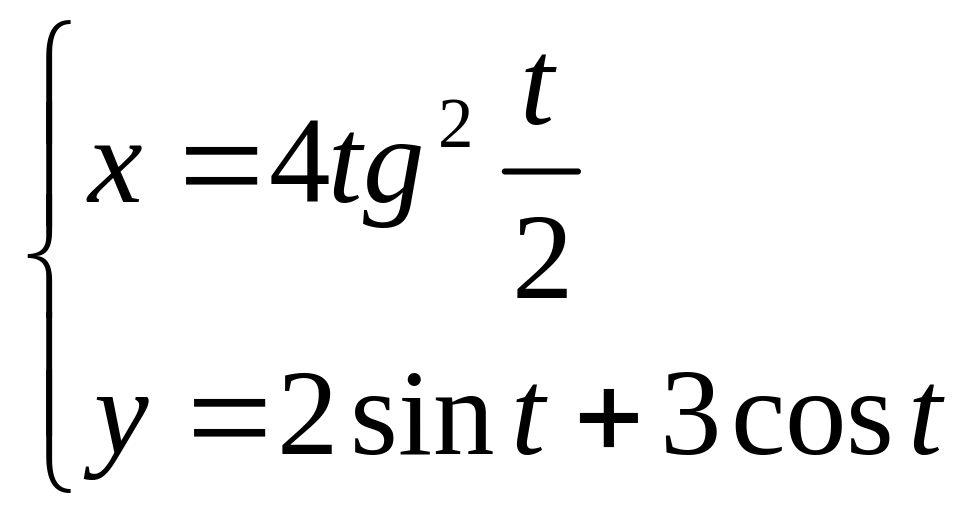
Варіант № 29 Варіант № 30
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.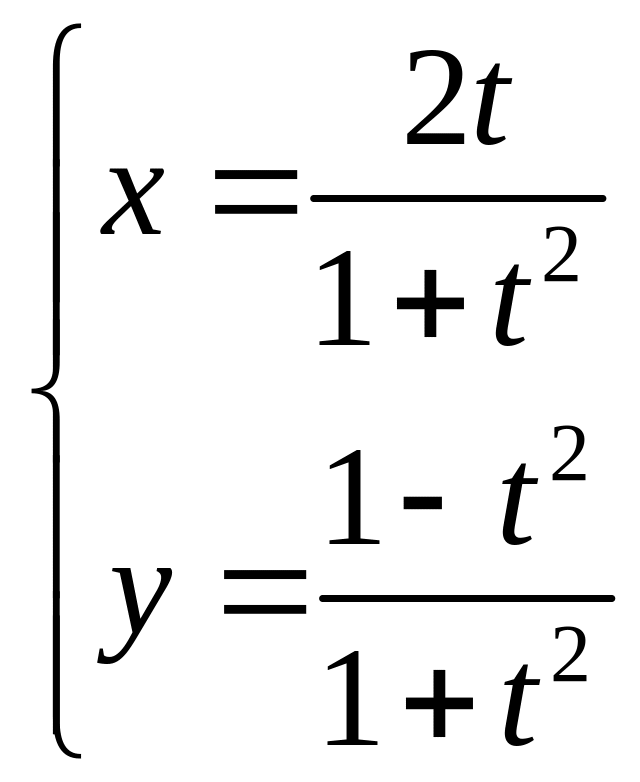 3.
3.
Завдання 7. Знайти границі функцій за правилом Лопіталя.
Варіант № 1 Варіант № 2
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.![]() 3.
3.![]()
Варіант № 3 Варіант № 4
1.![]() 1.
1.
![]()
2.![]() 2.
2.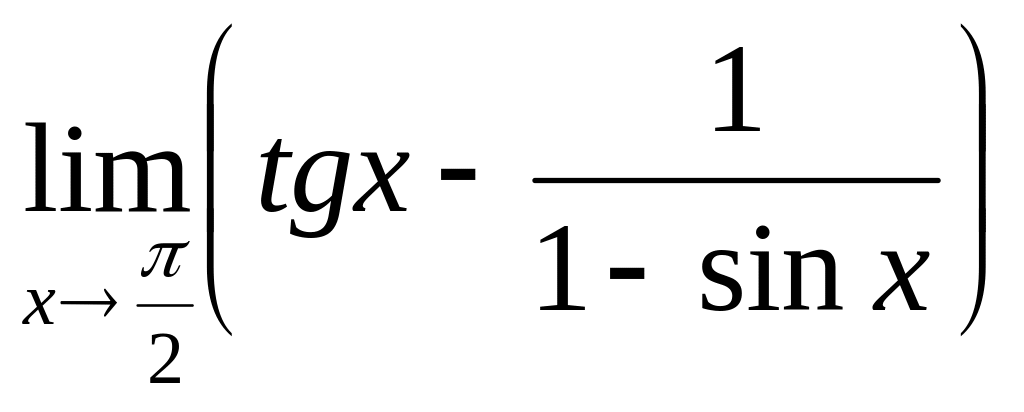
3.![]() 3.
3.
![]()
Варіант № 5 Варіант № 6
1.![]() 1.
1.
![]()
2.![]() 2.
2.
![]()
3.![]() 3.
3.
![]()
Варіант № 7 Варіант № 8
1.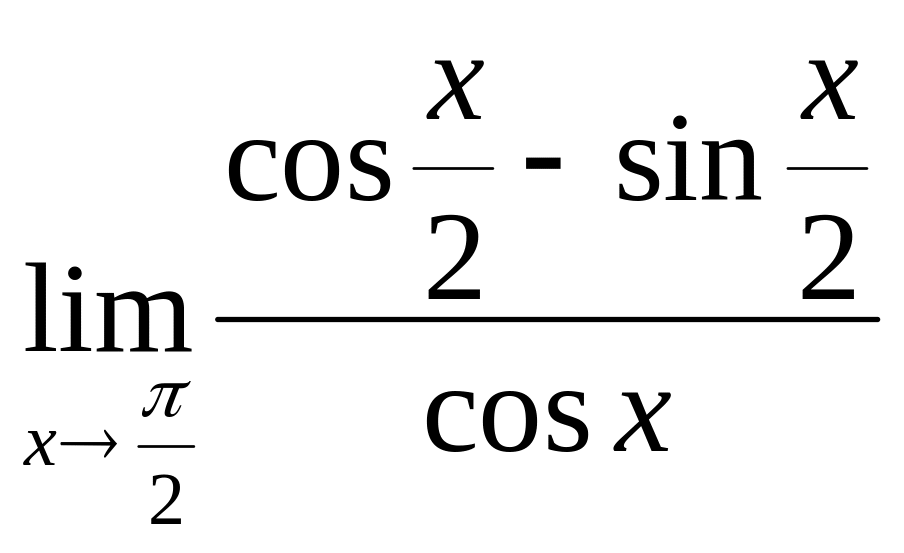 1.
1.![]()
2.
2.![]()
3.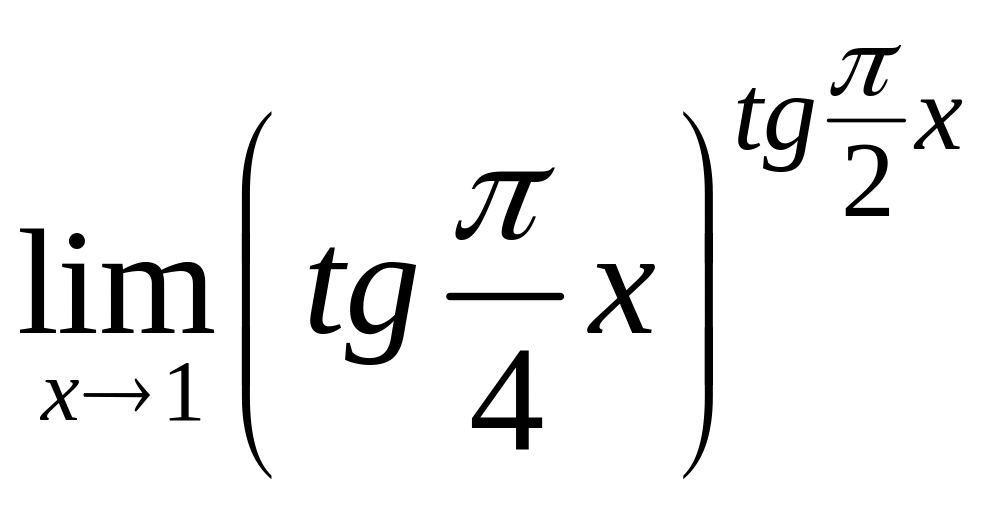 3.
3.![]()
Варіант № 9 Варіант № 10
1.![]() 1.
1.![]()
2. 2.
2.![]()
3. 3.
3.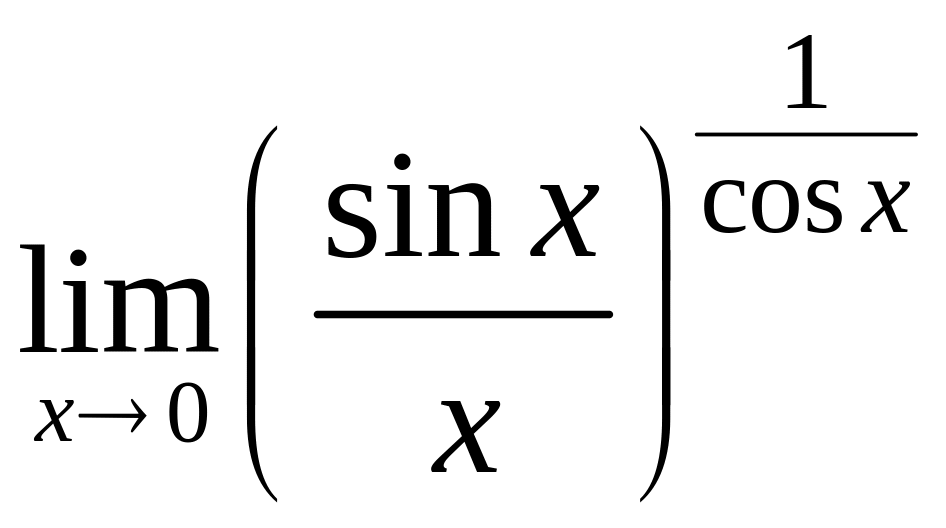
Варіант № 11 Варіант № 12
1.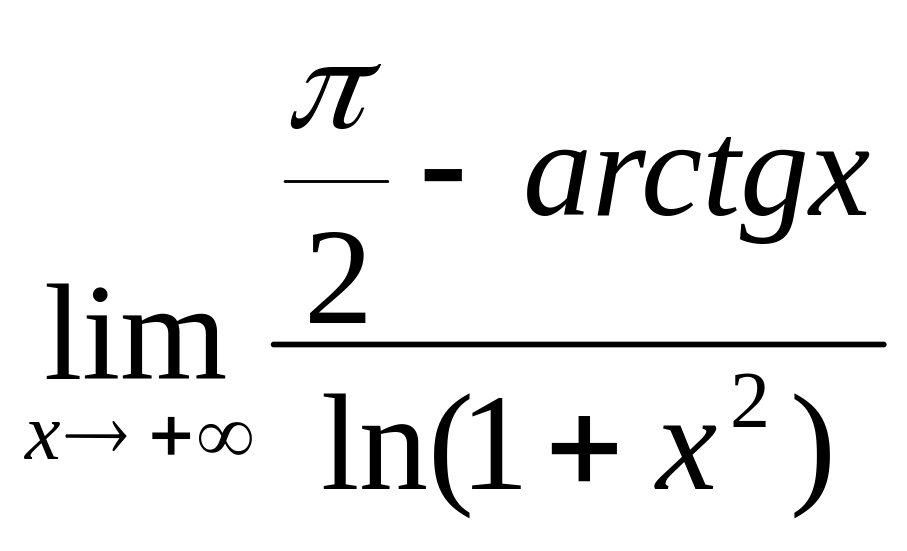 1.
1.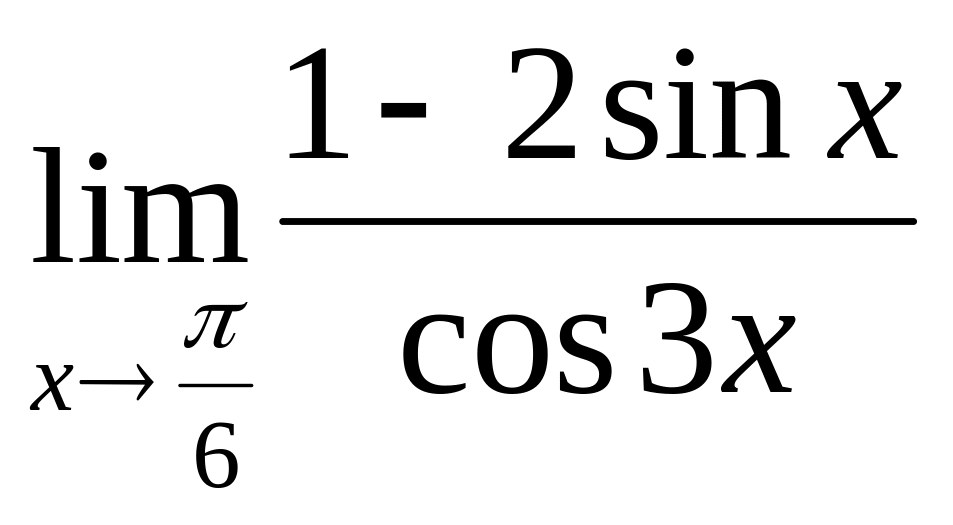
2.![]() 2.
2.![]()
3.![]() 3.
3.![]()
Варіант № 13 Варіант № 14
1.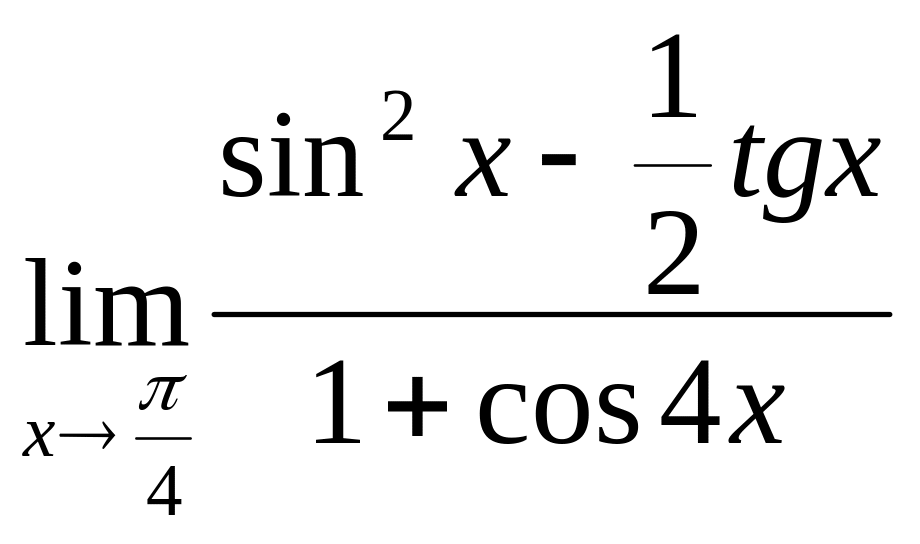 1.
1.
![]()
2.![]() 2.
2.
![]()
3.![]() 3.
3.![]()
Варіант № 15 Варіант № 16
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.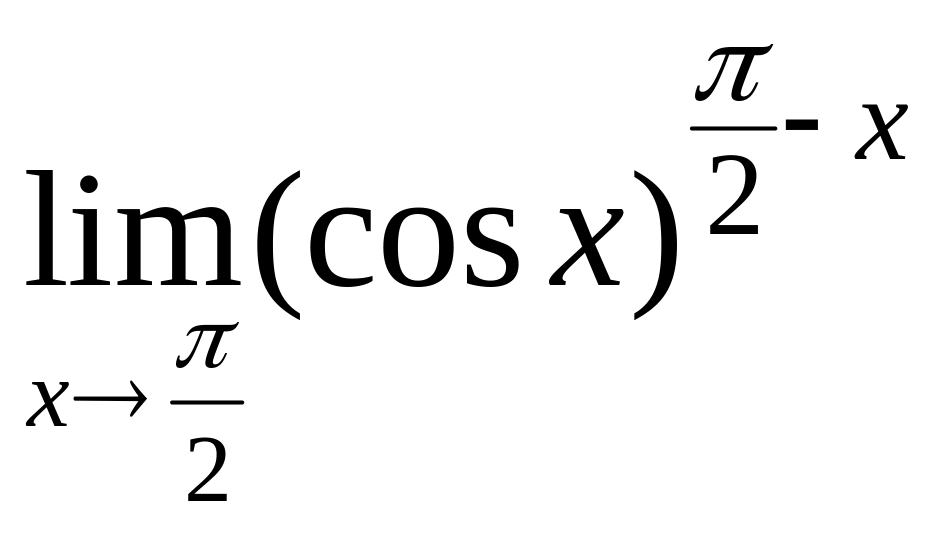 3.
3.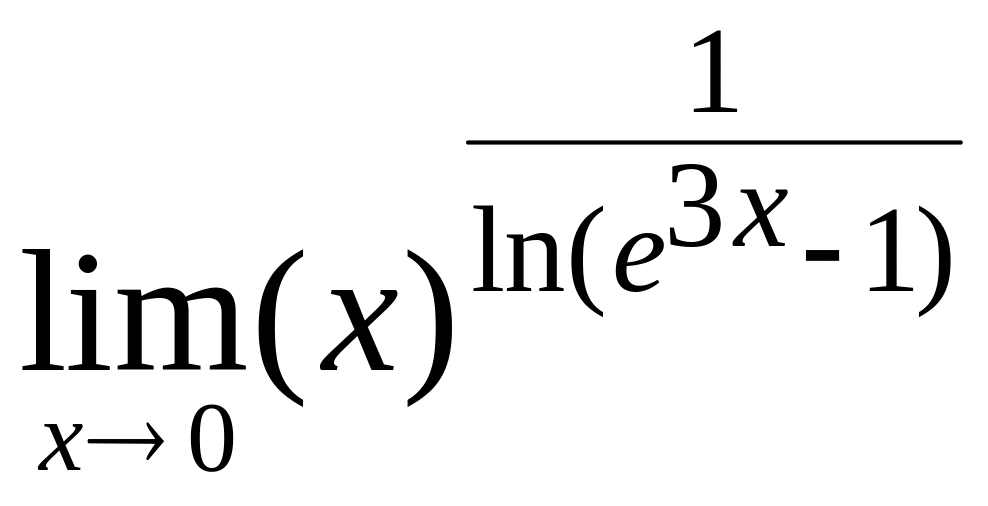
Варіант № 17 Варіант № 18
1.![]() 1.
1.![]() .
.
2.![]() 2.
2.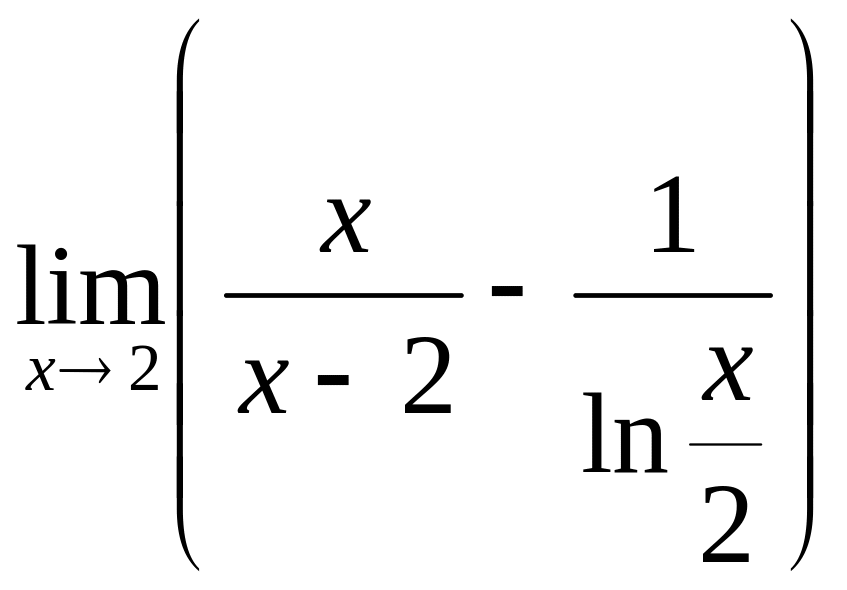
3.![]() 3.
3.
![]()
Варіант № 19 Варіант № 20
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.![]() 3.
3.![]()
Варіант № 21 Варіант № 22
1.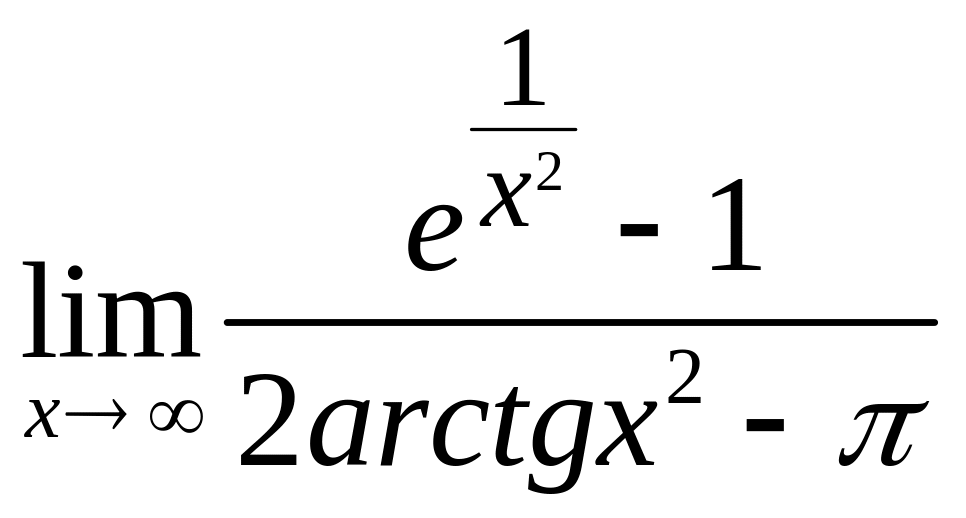 1.
1.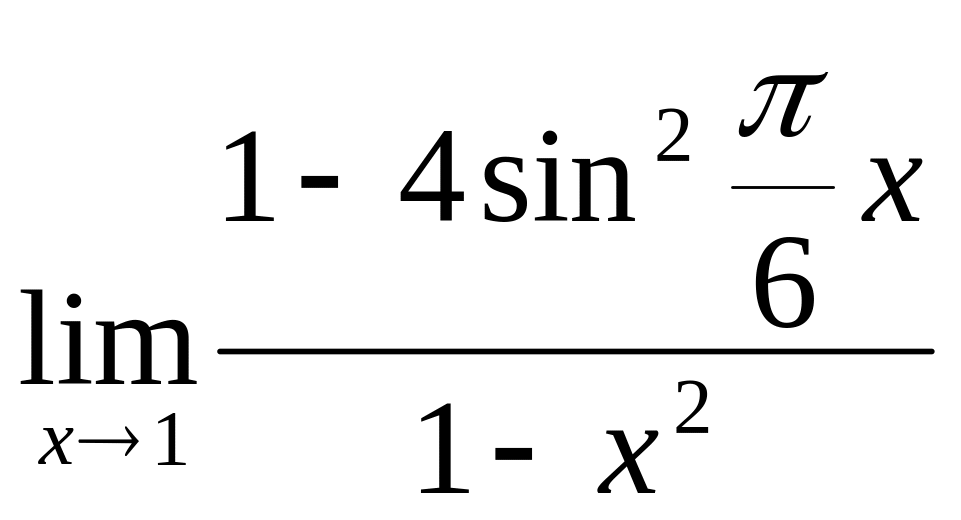
2.![]() 2.
2.![]()
3.
![]() 3.
3.![]()
Варіант № 23 Варіант № 24
1.![]() 1.
1.
2.![]() 2.
2.![]()
3.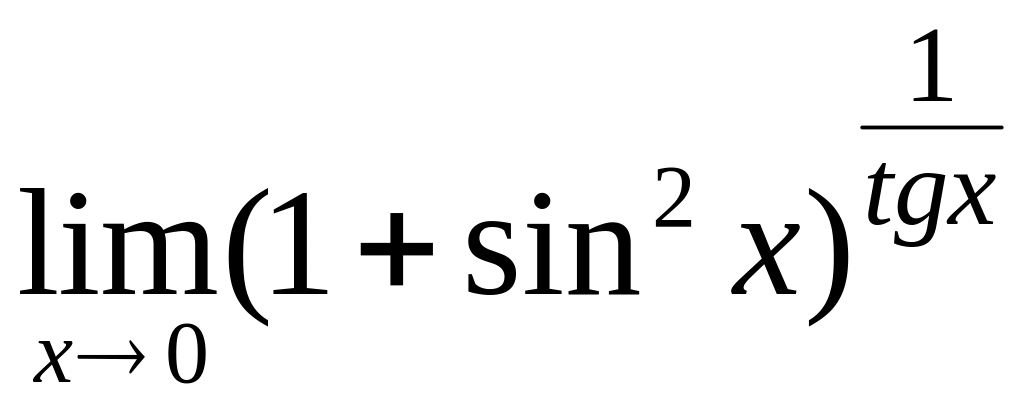 3.
3.![]()
Варіант № 25 Варіант № 26
1.![]() 1.
1.![]()
2.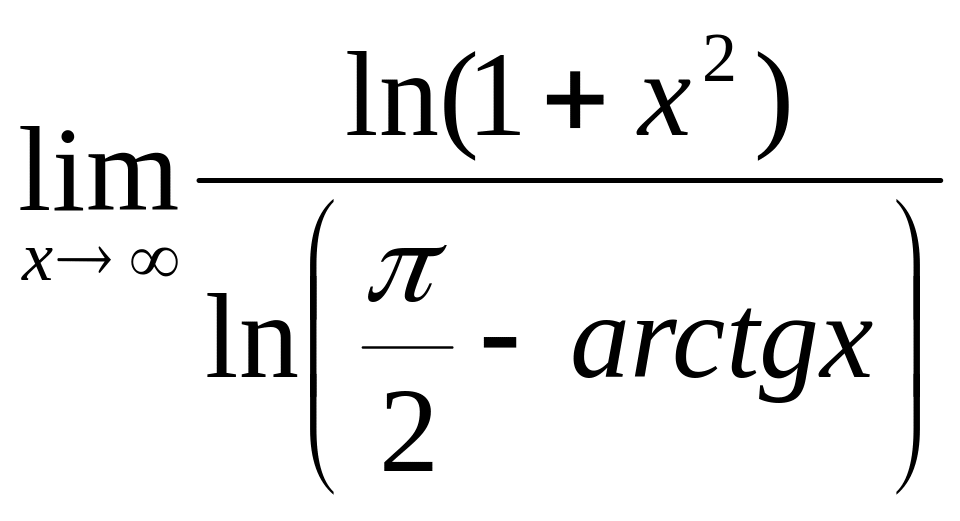 2.
2.![]()
3.![]() 3.
3.![]()
Варіант № 27 Варіант № 28
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3. 3.
3.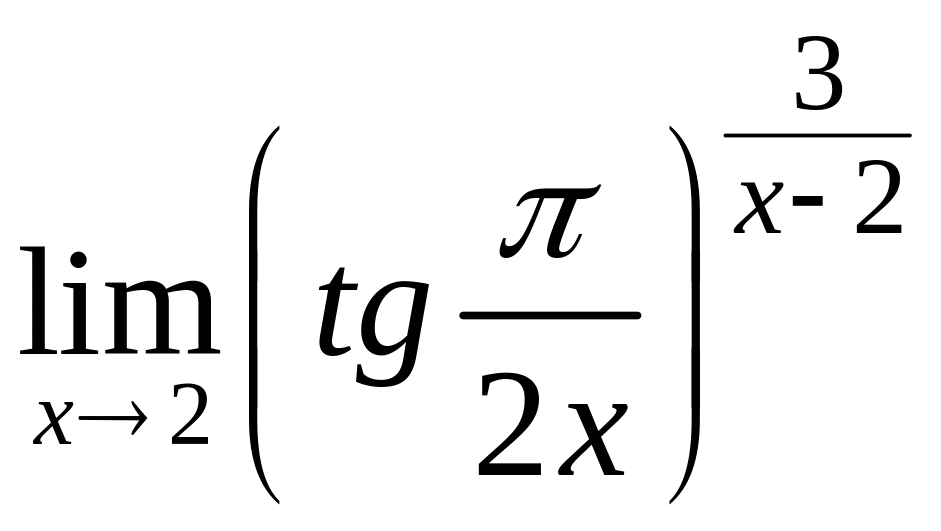
Варіант № 29 Варіант № 30
1.![]() 1.
1.![]()
2.![]() 2.
2.![]()
3.![]() 3.
3.![]()
Завдання 8. Скласти рівняння дотичної та нормалі, проведених до кривої
( - номер варіанта).
а)
![]() у точці перетину з віссю
у точці перетину з віссю
![]() ;
;
б)
![]() у точках її перетину з віссю
у точках її перетину з віссю
![]() ;
;
в)
![]() у точці , де
у точці , де
![]() .
.
Завдання 9. Знайти найбільше та найменше значення функції y = f(x)
на відрізку [a;b].
1.![]() 16.
16.
![]()
2.![]() 17.
17.![]()
3.![]() 18.
18.![]()
4.![]() 19.
19.![]()
5.![]() 20.
20.![]()
6.![]() 21.
21.![]()
7.![]() 22.
22.![]()
8.![]() 23.
23.![]()
9.![]() 24.
24.![]()
10.![]() 25.
25.![]()
11.![]() 26.
26.![]()
12.![]() 27.
27.![]()
13.![]() 28.
28.![]()
14.![]() 29.
29.![]()
15.![]() 30.
30.![]()
