Билет №5

 Центробежные насосы

В центробежном насосе передача энергии осуществляется за счет силового взаимодействия лопастного аппарата рабочего колеса с жидкостью.

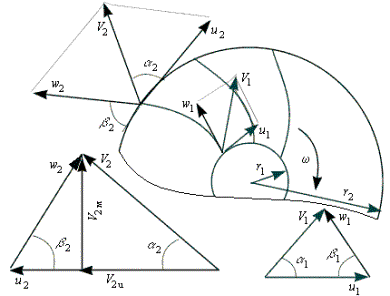
В межлопаточных каналах рабочего колеса частицы жидкости участвуют в сложном движении:

       переносном - вместе с рабочим колесом;

       относительном - по отношению к стенкам межлопаточных каналов;

       абсолютном - результирующем по отношению к вышеназванным движениям.

Вектор абсолютной скорости частицы  может быть представлен суммой переносной (окружной) скорости   и относительной скорости  .

Относительная скорость частицы   в любой точке профиля лопатки касательна к нему. Абсолютную скорость раскладывают на окружную V_iu и меридианную (расходную) V_iм составляющие, которые определяются по следующим формулам

где i=1,2. Индекс "1" - соответствует параметрам жидкости на входе в рабочее колесо, а "2" - на выходе из него.

(турбинное уравнение Эйлера)

Основное уравнение турбомашин связывает геометрические и кинематические характеристики рабочего колеса с развиваемым им напором. При его выводе принимают, что траектория частиц жидкости в межлопаточных каналах повторяет очертания профиля лопасти, т.е. для рабочего колеса делается допущение о бесконечности числа расположенных на нем бесконечно тонких лопаток (признаком этого будет служить символ  в качестве индекса).

Вывод основан на уравнении моментов количества движения при установившемся движении жидкости в равномерно вращающихся каналах, согласно которому изменение в единицу времени момента количества движения жидкости L, находящейся в канале, равно моменту действующих на нее внешних сил:

К внешним силам, действующим на жидкость в канале, относят силы, с которыми стенки канала действуют на жидкость, силы давления, силы трения, силы тяжести. Анализ показывает, что равнодействующие сил давления на внутренней и внешней образующих колеса проходят через ось вращения и момента не создают. Силы тяжести из-за симметрии рабочего колеса уравновешаны, а силы трения, действующие по периферийным поверхностям вращения малы. На основании вышеперечисленного предполагают, что момент создают только силы, возникающие от взаимодействия стенок рабочих каналов с жидкостью, находящейся в них.

Этот момент внешних сил связан с гидравлической мощностью насоса N_г и угловой скоростью вращения  следующим соотношением:

Подставляя найденные величины в закон изменения момента количества движения во времени получим уравнение Эйлера:

или

.                           (2.1)

Уравнение Эйлера связывает теоретический напор насоса со скоростями движения жидкости, которые зависят от подачи насоса, угловой скорости вращения рабочего колеса, а также с его геометрическими характеристиками.

Поток на входе в рабочее колесо создается предшествующим ему устройством (подводом). Следовательно момент скорости (закрутка)   определяется конструкцией подвода. Подводящие устройства многих насосов не закручивают поток и момент скорости на входе равен нулю. В этом случае теоретический напор определится по следующему уравнению:

где  - окружная скорость на периферии колеса.

Учитывая, что

,

где n - частота вращения, об/мин;

а проекция абсолютной скорости на выходе из колеса на окружную скорость, как следует из треугольника скоростей (см. рис. 2.1), определяется выражением

уравнение для теоретического напора примет вид:

          (2.2)

где b₂ - ширина канала рабочего колеса на выходе.

Теоретический напор при конечном числе лопастей H_т меньше  , что учитывается введением в уравнение Эйлера поправочного коэффициента 

.

Из рассмотрения треугольников скоростей (рис.2.1), на основании теоремы косинусов можно записать

откуда

С учетом приведенных зависимостей уравнение Эйлера может быть преобразовано к виду:

где   - напор, создаваемый за счет действия центробежных сил в потоке;

 - напор, создаваемый за счет изменения относительной скорости в канале рабочего колеса;

 - напор, создаваемый за счет изменения абсолютной скорости в канале рабочего колеса.

Величину   - называют статической частью напора, а   - динамической частью напора.

С целью уменьшения потерь в насосе желательно, чтобы статическая часть напора преобладала, причем за счет центробежной составляющей.