10. Кинетическая энергия

Найдем, как энергия тел зависит от их скорости.

Пусть на тело массой m действуетсила F (это может быть одна сила или равнодействующая нескольких сил), направленная вдоль перемещения, и скорость тела изменяется от до 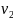(рис. 10.1).

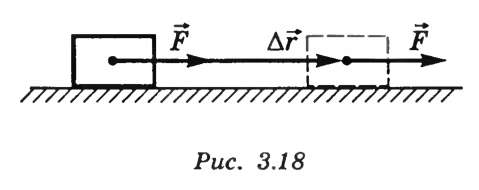
Рисунок 10.1. Движение тела под действием силы.

Работа этой силы A = FΔr.

По второму закону Ньютона F = ma.

При равноускоренном движении

Следовательно,

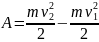
Физическая величина

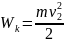
называется кинетической энергией.

Энергия, которой обладает тело вследствие своего движения, называется кинетической энергией.

Тогда

A = W_k2-W_k1=A

теорема о кинетической энергии:

изменение кинетической энергии тела равно работе равнодействующей всех сил, действующих на тело.

Эта теорема справедлива независимо от того, какие силы действуют на тело: сила упругости, сила трения или сила тяжести.

Если

Таким образом, кинетическая энергия тела равна работе, которую необходимо совершить, чтобы покоящемуся телу сообщить скорость.

Кинетическая энергия зависит от выбора системы отсчета.

11. Потенциальная энергия тела при гравитационном взаимодействии

Потенциальная энергия — это энергия системы, определяемая взаимным расположением тел (или частей тела друг относительно друга) и характером сил взаимодействия между ними.

Рассмотрим вначале некоторое тело, находящееся в гравитационном поле Земли.

При перемещении тела с высотыh₁ относительно нулевого уровня до высоты h₂ (рис. 11.1) сила тяжести совершает работу

А = mgh₁– mgh₂ = -(mgh₂– mgh₁).

W_n = mgh — потенциальная энергия тела в поле тяготения.

Тогда

А = - (W_n2 - W_nl) = -ΔW_n.

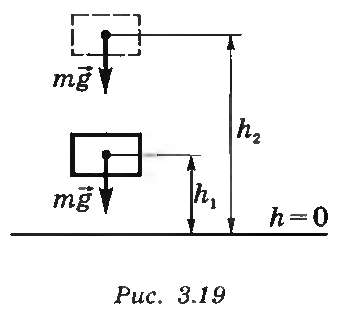
Рисунок 11.1. Движение тела в поле тяжести Земли.

Изменение потенциальной энергии тела, которое находится в гравитационном поле Земли, взятое со знаком "-", равно работе силы тяжести. Потенциальная энергия определяется с точностью до некоторой постоянной. Ее значение зависит от выбора нулевого уровня отсчета высоты. Потенциальную энергию какого-то положения (h₂=0) считают равной нулю (W_n2 =0), а энергию других положений (h₁ = h) отсчитывают относительно нулевого уровня:

W_n = mgh = А.

Таким образом, потенциальная энергия в поле тяготения — это энергия, обусловленная взаимодействием тела с Землей; она зависит от их взаимного положения и равна работе, которую совершает сила тяжести при перемещении тела из данного положения на нулевой уровень.

12. Потенциальная энергия упруго деформированного тела

При изменении величины деформации упруго деформированного тела от x₁ до х₂ сила упругости совершает работу

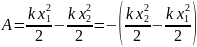
Величина

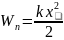
потенциальная энергия упруго деформированного тела.

А = -(W_n2 - W_nl) = -ΔW_n.

Если х₁ =0, х₂ = х, то

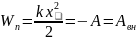
Потенциальная энергия упруго деформированного тела — энергия, обусловленная взаимодействием частей тела между собой. Она равна работе А_вн, которую совершают внешние силы, чтобы недеформированную пружину сжать (растянуть) на величину х.

13. Закон сохранения энергии в механике

Тела могут одновременно обладать и кинетической, и потенциальной энергией. Полная механическая энергия тела (системы тел) W — это сумма кинетической и потенциальной энергий:

W=W_n+W_K.

Рассмотрим замкнутую систему тел "тело—Земля", между которыми действует только консервативная сила — сила тяжести (см. рис. 11.1). Под действием этой силы изменяется и кинетическая, и потенциальная энергиятела. Причем

ΔW_K = Аи -ΔW_n = A

Т.е. увеличение кинетической энергии системы равно убыли ее потенциальной энергии. Из этих уравнений получаем

Δ(W_K + W_n) = 0 =>W_K + W_n = W = const.

Такой же результат получается и при действии силы упругости.

Закон сохранения энергии в механике: полная механическая энергия замкнутой системы тел взаимодействующих силами тяготения или силами упругости, остается постоянной.