4. Механическая работа

Действие силы, связанное с перемещением тела, характеризуется механической работой.

Механическая работа — это скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы на модуль перемещения и на косинус угла между ними:

A= FΔrcosa.

В СИ единицей работы является джоуль (Дж).

Здесь F = const и а = const на всем перемещении (рис. 4.1).

Рисунок 4.1. Работа при перемещении тела.

Работа — величина скалярная и может быть как положительной, так и отрицательной (рисунок 4.2).

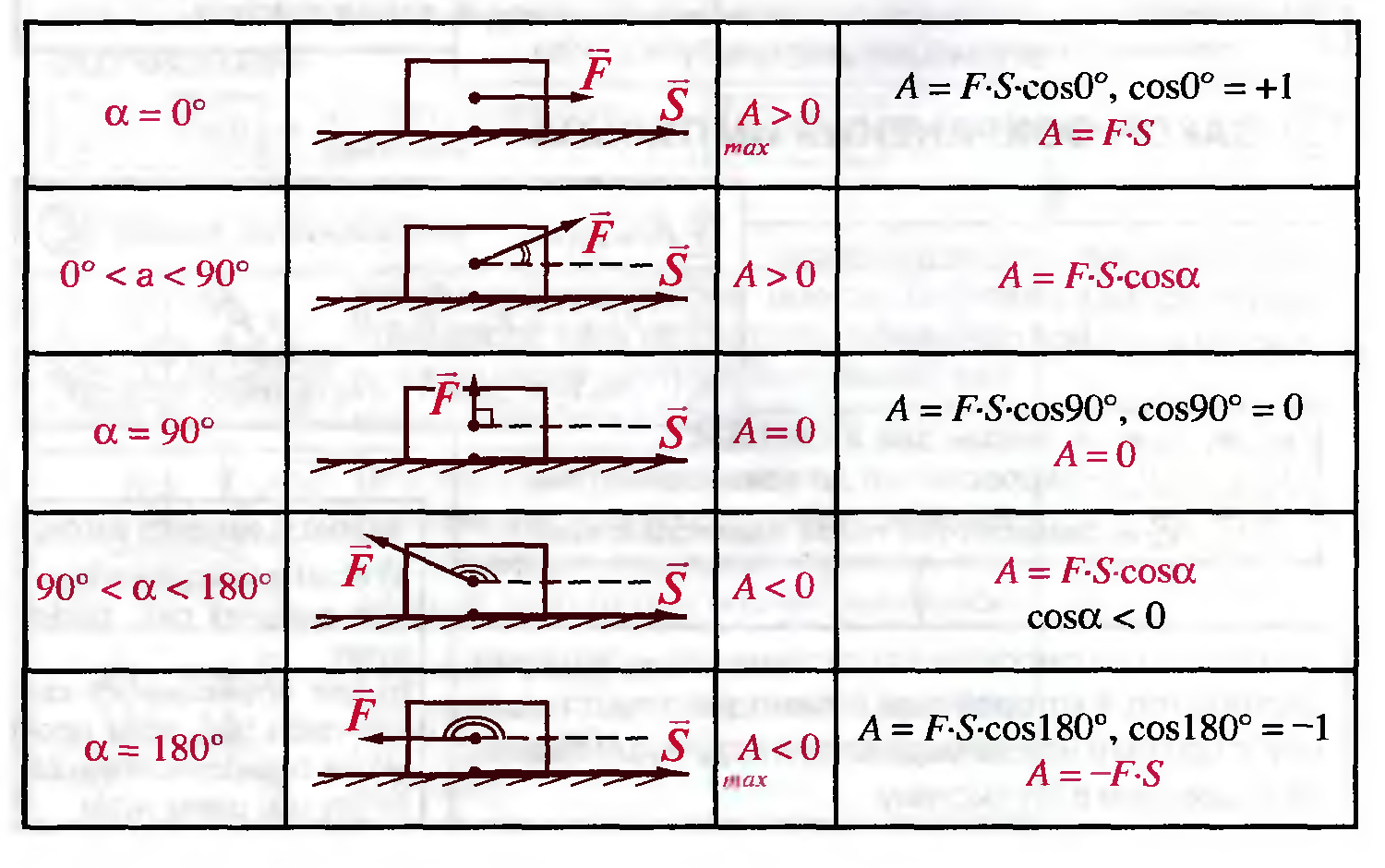
Рисунок 4.2. Зависимость работы от направления действия силы.

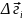В общем случае сила переменна, путь криволинеен, угол α изменяется произвольно. Тогда для определения работы нужно мысленно разбитьвсе перемещение на такие малые перемещения , на которых можно считать силу и угол неизменными, и найти элементарные работы по формуле

Работа на всем перемещении будет равна алгебраической сумме элементарных работ и тем точнее, чем меньше каждое перемещение и чем больше их число:

и в пределе при Δг→0

Работа силы F на всей траектории выражается интегралом, вычисляемым вдоль траектории, где 1 и 2 — радиус-векторы начальной и конечной точек траектории.

Для вычисления этого интеграла надо знать зависимость F(r) вдоль траектории. Для определения работы можно воспользоваться графическим методом (рис. 4.3, а, б, в).

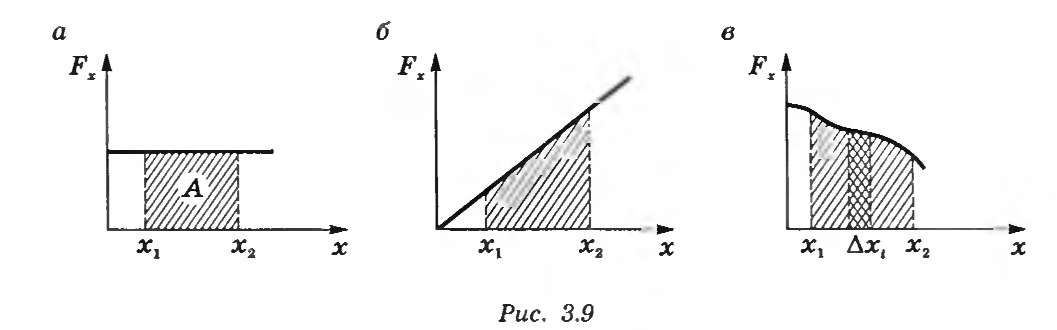
Рисунок 4.3. Графический метод для определения работы.

На графике F_x= f(x) работа на перемещении Δr_х = Δx численно равна площади заштрихованной фигуры. Работу можно представить как произведение средней силы на перемещение:

А = <F>Δг.

В частности, если сила изменяется линейно от F₁ до F₂ на данном перемещении, то ее среднее значение

и тогда работу можно рассчитать по формуле

Если к движущемуся телу приложено несколько сил, то каждая из них совершает работу, а общая работа равна алгебраической сумме работ, совершаемых отдельными силами.

5. Работа силы тяжести

Пусть тело перемещается вертикально вниз из положения 1 в положение 2, определяемые соответственно высотами h₁иh₂ над нулевым уровнем (рис. 5.1).

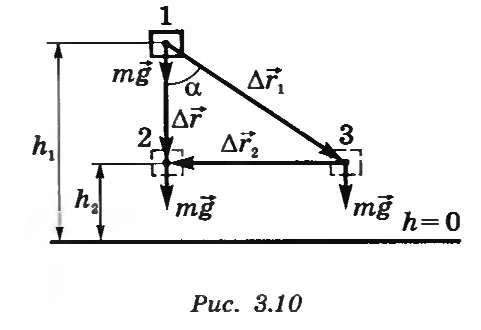
Рисунок 5.1. Работа силы тяжести.

Работа силы тяжести

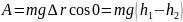
При перемещении тела из положения 1 в положение 2 по траектории 1—3—2 работа силы тяжести

А = А₁₃ + А₃₂.

Но

A_l3 = mgΔr₁cosα, A₃₂ = mgΔr₂cos90° = 0.

Из рисунка 5.1 видно, что

Δr₁cosα=h₁-h₂ =>A=mg(h_l~h₂).

Это значит, что работа силы тяжести не зависит от формы траектории движения тела, а зависит только от перемещения центра тяжести тела по вертикали. На замкнутой траектории работа силы тяжести равна нулю.

Силы, работа которых не зависит от формы траектории, а на замкнутой траектории равна нулю, называются консервативными. Следовательно, сила тяжести — консервативная сила.

6. Работа силы упругости

Пусть тело, прикрепленное к пружине и находящееся на гладком стержне, перемещается из положения 1 в положение 2 (рис. 6.1).

Рисунок 6.1. Движение тела на пружине.

Сила упругости, действующая на тело со стороны деформированной пружины, не остается постоянной, а изменяется согласно закону Гука пропорционально абсолютному удлинению:

F₁ =kx₁ и F₂ = kx₂.

Найдем работу силы упругости на этом перемещении по формуле

Более строгий вывод формулы для расчета работы силы упругости можно сделать, использовав метод интегрирования:

Можно показать, что работа силы упругости не зависит от формы траектории и на замкнутой траектории равна нулю. Она зависит только от взаимного положения частей тела. Сила упругости тоже консервативная сила.