1) Избыточность и сжатие. Расширения кода. Энтропия. Теорема кодирования для каналов связи без шума.

Избыточность (E)- это мера бесполезно совершаемых альтернативных выборов. Разность L - Н называют избыточностью кода.

Сжатие – процесс перекодирования данных с целью уменьшения их объема.

Расширение кода – кодирование комбинации символов (блока), а не каждого символа в отдельности. Расширения кода - блоки из n символов. При N-кратном расширении алфавита источника из символов s_i с заданными вероятностями p_i, каждый блок из n первоначальных символов становится одним символом t_i с вероятностью Q_i . Все вместе они образуют алфавит S_n=T.

Энтропия (Н) – мера неопределенности случайного объекта с конечным множеством состояний A_i , с соответствующими им вероятностями p_i. Величину Н называют средним количеством информации на знак, информацией на знак или энтропией источника сообщений. )

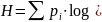Теорема Шеннона о кодировании без шума: для n-кратного расширения достаточно высокой кратности средняя длина кодового слова L может быть сколь угодно близкой к энтропии источника.

2) Измерение количества информации. Вероятностный, комбинаторный и алгоритмический подходы к измерению количества информации.

Подход к информации как к мере уменьшения неопределённости знания позволяет количественно измерять информацию. За единицу количества информации принято такое количество информации, которое содержит сообщение уменьшающее неопределённость знания в 2 раза. Такая единица названа бит.

Комбинаторное определение количества информации, исторически появившееся первым, характеризуется использованием математических функций, оперирующих с конечными множествами элементов, образующих какое-либо сообщение или систему.

Вероятностный подход к измерению информации основан на вероятностных допущениях относительно пребывания какой-либо системы в различных состояниях. При этом общее число элементов (микросостояний, событий) системы не учитывается.

Алгоритмический подход. За количество информации при этом, принимается значение некоторой функции от сложности каждого из объектов и длины программы (алгоритма) преобразования одного объекта в другой.

3) Методы обнаружения и коррекции ошибок в дискретных кодах. Корректирующие коды. Расстояние Хэмминга и его соотношение с корректирующей способностью кода. Аналоговый, дискретный, квантованный и цифровой сигналы.

Обнаружение ошибок в технике связи — действие, направленное на контроль целостности данных при записи/воспроизведении информации или при её передаче по линиям связи.

Исправление ошибок (коррекция ошибок) — процедура восстановления информации после чтения её из устройства хранения или канала связи.

В системах связи возможны несколько стратегий борьбы с ошибками:

- обнаружение ошибок в блоках данных и автоматический запрос повторной передачи повреждённых блоков (применяется в основном на канальном и транспортном уровнях);

- обнаружение ошибок в блоках данных и отбрасывание повреждённых блоков (применяется в системах потокового мультимедиа);

- обнаружение и исправление ошибок (применяется на физическом уровне).

Корректирующие коды — коды, служащие для обнаружения или исправления ошибок, возникающих при передаче информации под влиянием помех, а также при её хранении. Для этого при записи (передаче) в полезные данные добавляют специальным образом структурированную избыточную информацию (контрольное число), а при чтении (приёме) её используют для того, чтобы обнаружить или исправить ошибки. Естественно, что число ошибок, которое можно исправить, ограничено и зависит от конкретного применяемого кода.

Коды обнаружения ошибок могут только установить факт наличия ошибки в переданных данных, но не исправить её. Используемые коды обнаружения ошибок принадлежат к тем же классам кодов, что и коды, исправляющие ошибки. Фактически, любой код, исправляющий ошибки, может быть также использован для обнаружения ошибок (при этом он будет способен обнаружить большее число ошибок, чем был способен исправить).

По способу работы с данными коды, исправляющие ошибки, делятся на:

- блоковые коды, делящие информацию на фрагменты постоянной длины и обрабатывающие каждый из них в отдельности;

- свёрточные коды, работающие с данными как с непрерывным потоком.

Минимальное расстояние Хемминга является важной характеристикой линейного блокового кода. Она показывает насколько "далеко" расположены коды друг от друга. Она определяет другую, не менее важную характеристику - корректирующую способность: 2t < d_min Корректирующая способность определяет, сколько ошибок передачи кода можно гарантированно исправить.

Под аналоговым сигналом понимают сигнал, непрерывный во времени и принимающий значение из какого-то промежутка значений.

Дискретный сигнал представляется в виде последовательности значений, взятых в дискретные моменты времени.

В квантовом сигнале область значений сигнала разбивается на уровни, количество которых должно быть представлено в числах заданной разрядности.

Под цифровым сигналом понимается сигнал, полученный из аналогового путем квантования по амплитуде и дискретизации по времени.

Детерминированными сигналами называются сигналы, значения которых в любые моменты времени являются известными величинами или могут быть заранее вычислены.

Случайным сигналом является такой, значения параметров которого случайны и заранее не известны и могут быть определены с некоторой степенью вероятности.