1. Случайные события. Пусть в результате испытания единственно возможно появление n несовместных равновероятных событий e1, e2,…, En .

Понятие равновероятности является неопределяемым и интуитивным. Несовместными будем считать события, которые исключают появление друг друга. Такие события будем называть элементарными. Множество элементарных исходов относительно произведенного испытания называется пространством элементарных событий и обозначается Ω(омега).Случайным событием называется любое множество элементарных событий. Случайные события обозначаются большими латинскими буквами, а числа маленькими латинскими буквами. Множества событий обозначаются греческими буквами. Дадим определения действиям над событиями: 1. Если при выполнении события А всегда происходит и событие B, то говорят, что событие А влечет за собой событие В и обозначают А B. 2. Если А B и В А, то говорят, что события А и В равновозможны и обозначают А=В. 3. Событие, состоящее в том, что появится хотя бы одно из событий А или В называют суммой событий и обозначается А+В. 4. Событие, состоящее в том, что события А и В появятся одновременно, называется произведением событий и обозначается А*В .5. Событие, состоящее в том, что А произойдет, а В не произойдет, называется разностью: А-В. 6. Событие называется достоверным, если оно с необходимостью (точно) происходит, и обозначается Ω (омега). 7. Событие называется невозможным, если оно не может произойти, и обозначается Ø. 8. События А и В называются несовместными, если их одновременное появление невозможно

Ø. 9.События А и называются противоположными, если их одновременное появление невозможно и в сумме они дают пространство элементарных событий

Ø, . 10. События В₁, ..., В_n образуют полную группу, если любые 2 из них одновременно появится не могут и в сумме они дают пространство элементарных событий. Ø,

.2. Классическое определение вероятности и ее свойства. Классической вероятностью называется отношение числа несовместных равновероятных событий, составляющих А, к общему числу элементарных событий . Формула классической вероятности позволяет решать ограниченное число задач: 1) число элементарных событий конечно, 2) все элементарные событий равновозможны. Теория вероятности пользуется языком теории множеств, т.е. события это множества, а действия над событиями – действия над множествами. Случайные события обозначаются большими латинскими буквами, а числа маленькими латинскими буквами. Множества событий обозначаются греческими буквами. Свойства классической вероятности: 1. Для любого события вероятность есть число неотрицательное: . 2. Теорема сложения: Если событие А можно представить в виде 2 несовместных события В и С, то вероятность события А равна сумме вероятностей В и С . 3. Вероятность достоверного события равна единице , т.к. . 4. Вероятность противоположного события равна . 5. Вероятность невозможного события равна 0: P(Ø) = 0 , т.к. m = 0. 6. Если событие А влечет за собой событие В, то . 7. Для любого события . 8. Р(В+С) ≤ Р(В) + Р(С) непревосходит

4. Условная вероятность. Независимость событий. Часто интересует вероятность того, что произойдёт событие А при условии, что некоторое событие В уже произошло. Такую вероятность называют условной и обозначают P(A/B). Опр. Условной вероятностью события А при условии, что событие В уже произошло, называется отношение . (3.1) Аналогично, условной вероятностью события B при условии, что событие A уже произошло, называется (3.2) Из формул (3.1) и (3.2) получим теорему умножения: (3.3) Вероятность произведения двух произвольных событий равна произведению вероятности одного из событий на вероятность второго, при условии, что первое уже произошло. Распространим теорему умножения на конечное число событий: Опр. События А и В называются независимыми, если вероятность произведения равна произведению вероятности этих событий. . (3.4) Из (3.3) и (3.4) получим: . Следовательно, для независимых событий условная и безусловная вероятности совпадают . Для конечного числа независимых событий вероятность произведения равна произведению вероятностей: .

3.Формулы комбинаторики. Гипергеометрическое распределение. Комбинаторика-раздел матем, котором изуч. Задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам,в частности о подсчете числа комбинаций, получаемых из элементов заданного конечного множества. В каждом опыте важным является способ выбора элементов. Существуют 2 схемы выбора элементов: схема выбора без возвращения элементов и схема выбора с возвращением элементов. Рассмотрим сначала схему выбора без возвращений. Пусть дано множество, состоящее из n различных элементов. Перестановками назыв. Комбинации, составленные из одних и тех же элементов, которые отличаются только порядком их следования. Число перестановок из n элементов вычисляется по ф-ле: Pn=n!. Размещениями назыв. Комбинации, составленные из n элементов по m(0<m≤n), которые различаются либо составом элементов, либо порядком их следования. Число размещений из n элементов по m вычисляется по ф-ле;

Сочетаниями назыв. Комбинации , составленные из n элементов по m(0<m≤n), которые различаются составом элементов. Чичло сочетаний из n элементов по m вычисляется по ф-ле;

Свойства сочетаний: 1)С =1 т.к. по определения 0!=1; 2)С =n; 3)С =С .

Урновая схема:

Это ф-ла называется гипергеометрическим распределением. Схем а выбора с возвращением. Если при выборке m элементов из n элементов возвращаются обратно и упорядочиваются, то говорят что размещения с повторениями. Размещения с повторениями могут отличаться друг от друга элементами, порядком и количеством повторений элементов. Обозначаются они Аn=n .Если при выборке элементов из n элементов возвращаются обратно без последующего упорядочивания, то говорят что сочетания с повторениями. Число сочетаний с повторениями обозначаются С =С . Пусть в мн-ве с n-элементами есть k различных эл-нтов, при это первый элемент повторяется n раз, второй эл-нт n раз…, k-й элемент- n раз, причем n +n +…+n =n. Перестановками из n-эл-в данного множество называют перестановками из n-эл-в и обозначают

5. Формула полной вероятности. Формула Байеса. Пусть событие А может произойти только с одним из n несовместных событий H₁…H_n, образующих полную группу, т.е. Ø, , . Так как события и несовместны, то и ( ) и ( ) являются несовместными. Тогда по теореме сложения Применяя теорему умножения к каждому слагаемому, получим формулу полной вероятности: . (4.1) События H₁, H₂,…, H_n часто называют гипотезами. Иногда интересует, как перераспределятся вероятности гипотез, после того, как событие А уже произошло: . По теореме умножения , . Подставляя в знаменатель формулу полной вероятности, получим формулу Байеса: . (4.2)

6. Схема независимых испытаний Бернулли. Пусть производится последовательность независимых испытаний с 2 исходами: событие А или появится или не появится. , , Под элементарным событием в схеме Бернулли принимается последовательность наступлений и ненаступлений события А в n испытаниях. Обозначим А={1}, ={0}. Тогда элементарный исход можно представить в виде вектора, состоящего из нулей и единиц: (1,0,…, 1). Найдем вероятность того, что в n испытаниях событие появится ровно m раз. Найдем сначала вероятность того, что в 3-х испытаниях событие А появится 2 раза при условии, что вероятность наступления в одном испытании равна p. При этом возможны следующие элементарные исходы

(1,1,0); (0,1,1); (1,0,1).Вероятность каждого элементарного исхода одинакова и равна p²q. Таким образом, вероятность того, что в 3-х испытаниях событие наступит 2 раза

Для произвольных m и n вероятность одного элементарного исхода равна p^mq^n-m . Число таких элементарных исходов равно числу способов разместить m единиц по n местам, а это по определению есть число сочетаний из n элементов по m. Получим формулу Бернулли . (5.1)

При изменении m от 0 до n вероятность в формуле Бернулли сначала растет, а потом 4убывает, то число m₀ при котором эта вероятность достигает максимального значения наз. наивероятнейшим. Можно показать, что это число равно Если m₀ не является целым числом, то его следует округлить до ближайшего целого с избытком, а если m₀ целое число, то наивероятнейших чисел 2. _. Часто интересует вероятность появления события А не ровно m раз, а от m₁ до m₂ раз включительно 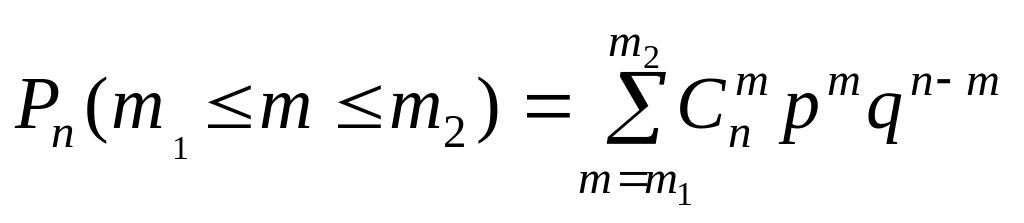(5).

7. Функция распределения вероятности и ее свойства. Одним из основных понятий ТВ является СВ (случайная величина). СВ бывают дискретные, непрерывные и др. Для того чтобы одинаковым способом характеризовать СВ различной природы вводится понятие функции распределения вероятностей. Опр. Пусть - случайная величина и . Вероятность того, что примет значение, меньшее чем , называется функцией распределения вероятностей: .Функция распределения вероятностей является неслучайной функцией, а функцией, вычисленной на основании закона распределения случайной величины. Случайной называется величина, значения которой зависят от случая и для которой определена функция распределения вероятностей. Дискретной называется случайная величина, которая принимает конечное или счетное множество значений. Счетное множество – число натуральных чисел. Для полной вероятностной характеристики дискретной случайной величины необходимо знать ее закон распределения. Пусть – возможные значения случайной величины , - вероятности этих значений.Множество пар , i =1,2,… называется законом распределения вероятностей дискретной случайной величины.

Обычно закон распределения изображается в виде таблицы:

					…
P					…

Рис. 7.1 График функции распределения

Опр. Непрерывной называется СВ(случайная величина), значения которой заполняют сплошь некоторые промежутки.

Свойства функции распределения 1. , 0 , т.к. это вероятность.

2 . –неубывающая функция.

Следствия 2.1. Вероятность попадания случайной величины в заданный интервал есть приращение функции распределения на этом интервале:

2.2. Вероятность принять одно фиксированное значение для непрерывной СВ равна 0

, т.к. функция распределения непрерывной СВ непрерывна.

2.3. Вероятность попадания непрерывной СВ в открытый или замкнутый промежуток одинакова:

Докажем последнее равенство 4. непрерывна слева в каждой точке (см. рис.7.1).

5. .