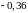Тема: «Вступление к теории вероятности»
Вариант № 1
1. Партия деталей состоит из 150 деталей I сорта, 30 деталей II сорта, 16 деталей III сорта, 4 детали бракованных. Какова вероятность того, что отобранная наудачу деталь будет I или II сорта?
2. В ящике 10 изделий завода А и 5 изделий завода В. Вероятность быть стандартным для изделия завода А – 0,8; для изделия завода В – 0,6. Какова вероятность того, что взятая наудачу деталь стандартная?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4.
Случайная величина
задана функцией распределения
.
Найти плотность вероятностей,
математическое ожидание и дисперсию
.
5.
В результате
наблюдений за
получена выборка объема
.
а) Определить
для выборки основной промежуток
,
количество интервалов распределения
,
построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить
числовые характеристики выборки,
являющиеся оценками параметров
распределения
и
.
Выдвинуть гипотезу о возможном нормальном
законе распределения
.
2,02 |
0,87 |
1,96 |
5,13 |
5,12 |
4,96 |
7,20 |
1,86 |
7,43 |
2,01 |
9,93 |
1,96 |
3,11 |
1,92 |
4,36 |
4,83 |
2,33 |
6,01 |
5,40 |
9,26 |
0,33 |
3,24 |
1,42 |
7,26 |
1,65 |
7,67 |
5,20 |
3,78 |
5,51 |
7,84 |
– 0,07 |
0,17 |
5,10 |
3,55 |
4,36 |
4,26 |
6,76 |
6,28 |
7,48 |
– 0,20 |
7,13 |
5,24 |
6,38 |
4,29 |
1,55 |
4,46 |
6,35 |
4,09 |
7,53 |
2,53 |
Вариант № 2
1. Производится выстрел во вращающийся диск, разбитый на 12 секторов, раскрашенных попеременно в желтый, зеленый, красный цвет. Найти вероятность попадания в желтый сектор.
2.
Устройство состоит из 1000 элементов,
работающих независимо один от другого.
Вероятность отказа любого элемента в
течение времени
равна 0,002. Найти вероятность того, что
за время
откажут ровно три элемента.
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить
числовые характеристики выборки,
являющиеся оценками параметров
распределения
и
.
Выдвинуть гипотезу о возможном нормальном
законе распределения
.
5,18 |
1,49 |
2,97 |
6,10 |
3,26 |
4,89 |
2,52 |
2,55 |
1,67 |
4,95 |
4,27 |
6,34 |
1,43 |
0,92 |
1,90 |
5,87 |
5,48 |
2,11 |
6,93 |
4,03 |
6,96 |
4,05 |
4,95 |
3,41 |
3,92 |
0,84 |
2,70 |
3,26 |
4,89 |
5,27 |
4,38 |
2,70 |
3,06 |
1,87 |
5,78 |
6,49 |
2,17 |
5,93 |
3,18 |
4,12 |
|
4,32 |
5,75 |
2,79 |
1,63 |
2,96 |
2,94 |
3,32 |
4,35 |
5,90 |
Вариант № 3
1. Монета брошена три раза. Найти вероятность того, что при этом герб выпадает два раза.
2. В корзине 15 теннисных мячиков, из них девять новых, остальные уже использовались. Для определенной игры берется мяч наугад и затем возвращается в корзину. Какова вероятность взять новый мяч для следующей игры?
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
5,28 |
5,30 |
6,99 |
5,83 |
4,21 |
5,20 |
4,24 |
6,44 |
4,99 |
5,85 |
3,96 |
3,99 |
4,94 |
4,87 |
6,21 |
6,27 |
3,09 |
3,83 |
5,01 |
4,86 |
5,93 |
4,92 |
4,35 |
6,87 |
4,70 |
4,50 |
4,82 |
3,56 |
3,41 |
4,78 |
7,74 |
3,59 |
5,12 |
6,05 |
5,77 |
4,50 |
6,11 |
4,60 |
5,10 |
4,73 |
5,25 |
4,08 |
6,32 |
6,22 |
4,55 |
4,34 |
5,88 |
4,63 |
4,18 |
7,31 |
Вариант № 4
1. Бросаются две (2) монеты. Какова вероятность того, что на одной из них выпадет герб, а другой цена?
2.
Вероятность
того, что расход электроэнергии на
протяжении одних суток не превысит
норму, которая равна
.
Найти вероятность того, что на ближайшую
неделю расход электроэнергии будет
нормальным только в течение трех суток.
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить
числовые характеристики выборки,
являющиеся оценками параметров
распределения
и
.
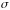Выдвинуть гипотезу о возможном нормальном
законе распределения
.
15,47 |
13,52 |
9,82 |
16,57 |
16,22 |
6,82 |
14,87 |
9,92 |
22,27 |
16,97 |
10,77 |
13,17 |
16,12 |
20,47 |
22,42 |
12,82 |
19,87 |
21,17 |
15,52 |
12,87 |
15,87 |
20,82 |
12,57 |
20,72 |
10,65 |
19,67 |
18,37 |
13,62 |
15,52 |
16,07 |
14,22 |
14,92 |
16,22 |
16,77 |
13,87 |
18,62 |
7,97 |
16,87 |
13,07 |
9,37 |
15,72 |
14,62 |
19,52 |
22,92 |
15,72 |
18,67 |
16,27 |
12,92 |
20,52 |
15,87 |
Вариант № 5
1. Бросаются 3 игральные кости одновременно. Какова вероятность, что при этом выпадет 10 очков?
2. В пирамиде 8 винтовок, 6 из которых с оптическим прицелом. Вероятность попадания из оптической винтовки – 0,95; из обычной – 0,7. Найти вероятность поражения цели из наугад выбранной винтовки.
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
10,14 |
6,81 |
7,08 |
9,46 |
9,74 |
6,53 |
8,56 |
8,37 |
5,73 |
7,24 |
6,55 |
6,98 |
4,83 |
6,77 |
5,28 |
7,19 |
4,60 |
8,32 |
4,83 |
8,44 |
9,78 |
11,53 |
5,43 |
5,17 |
8,59 |
7,57 |
7,90 |
5,76 |
8,37 |
7,31 |
6,18 |
6,58 |
7,17 |
6,15 |
6,46 |
8,59 |
6,87 |
7,48 |
8,12 |
5,29 |
6,25 |
6,28 |
6,32 |
8,55 |
10,33 |
5,5 |
8,37 |
7,79 |
6,79 |
4,34 |
Вариант № 6
1. 10 книг расставляются на полке в случайном порядке. Среди них «Путешествия Гулливера» и «Приключения Тома Сойера». Найти вероятность того, что эти книги могут оказаться рядом.
2. В ящике 10 изделий завода А и 5 изделий завода В. Вероятность быть стандартным для изделия завода А – 0,8; для изделия завода В – 0,6. На удачу вынутая деталь оказалась стандартной. Какова вероятность того, что ее изготовил завод А?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
10,22 |
7,95 |
9,5 |
9,11 |
10,19 |
8,64 |
6,11 |
11,68 |
11,02 |
10,55 |
8,7 |
10,02 |
8,95 |
12,01 |
8,53 |
8,09 |
8,8 |
8,2 |
6,8 |
8,2 |
7,35 |
6,8 |
6,71 |
8,45 |
8,26 |
8,67 |
7,65 |
7,84 |
6,13 |
10,41 |
10,8 |
6,6 |
7,68 |
10,11 |
8,2 |
11,51 |
11,65 |
7,32 |
10,13 |
5,75 |
8,92 |
9,33 |
6,77 |
9,42 |
7,54 |
7,07 |
9,28 |
13,41 |
7,46 |
6,49 |
Вариант № 7
1. В ящике имеется десять (10) деталей, из которых одна дефектная. Какова вероятность того, что среди трех вынутых деталей нет дефектных?
2.
Вероятность
попадания в цель при стрельбе из трех
орудий соответственно равны: для первого
орудия –
,
для второго орудия –
,
для третьего орудия –
.
Найти вероятность того, что при
одновременном залпе из всех орудий цель
будет поражена.
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
2,66 |
4,25 |
3,84 |
2,70 |
4,90 |
8,74 |
0,17 |
1,80 |
5,19 |
2,42 |
4,66 |
5,19 |
9,64 |
3,43 |
0,98 |
3,96 |
6,82 |
2,98 |
5,97 |
4,66 |
4,33 |
5,87 |
4,41 |
5,64 |
6,25 |
6,66 |
2,54 |
0,53 |
2,90 |
5,52 |
2,58 |
|
3,89 |
0,13 |
3,68 |
10,42 |
0,82 |
6,37 |
1,56 |
2,78 |
2,40 |
0,57 |
4,50 |
5,07 |
3,84 |
2,05 |
5,52 |
5,07 |
2,62 |
2,78 |
Вариант № 8
1. В партии из 32 деталей 4 бракованных. Наудачу вынимают 4 детали. Какова вероятность, что среди них будет хотя бы 1 бракованная?
2.
Производится
сортировка стеклянных изделий. Вероятность
события
(при сортировке изделие может быть
разбито) равна 0,004. Найти вероятность
того, что из 1000 изделий, подвергнутых
сортировке, будут разбиты 5.
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
11,74 |
15,31 |
13,69 |
15,93 |
19,09 |
10,82 |
13,32 |
12,79 |
9,08 |
11,03 |
21,54 |
13,4 |
7,09 |
10,62 |
20,79 |
10,58 |
10,16 |
7,48 |
13,44 |
15,14 |
7,88 |
11,78 |
12,61 |
10,78 |
10,95 |
8,83 |
8,91 |
11,7 |
10,37 |
7,67 |
12,94 |
17,35 |
13,73 |
13,44 |
8,46 |
11,9 |
13,4 |
13,98 |
15,44 |
11,49 |
14,44 |
13,48 |
14,77 |
15,52 |
14,19 |
11,36 |
11,16 |
9,62 |
10,82 |
11,20 |
Вариант № 9
1. В урне имеются карточки с буквами р, т, а, с, л, е. Карточки вынимаются по очереди наугад и располагаются в последовательности слева на право. Какова вероятность, что при этом составится слово «стрела»?
2. Вероятность попадания в баскетбольную корзину у игрока N равна 0,9, а у игрока M равна 0,95.Для штрафного броска в корзину был на удачу вызван один из них, бросок оказался удачным. Какова вероятность, что был вызван N?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
1,18 |
1,45 |
1,75 |
1,98 |
1,61 |
2,78 |
2,21 |
0,48 |
1,70 |
1,10 |
||
1,86 |
0,96 |
4,32 |
2,94 |
2,61 |
1,02 |
1,70 |
1,40 |
1,16 |
2,26 |
||
0,74 |
1,58 |
1,03 |
0,90 |
1,25 |
2,41 |
0,45 |
1,94 |
1,43 |
2,74 |
||
2,14 |
1,32 |
2,11 |
2,47 |
1,13 |
0,75 |
1,89 |
0,25 |
2,82 |
4,94 |
||
1,70 |
1,50 |
1,66 |
1,26 |
1,63 |
2,97 |
1,80 |
1,37 |
3,14 |
2,85 |
||
Вариант № 10
1. В урне находятся три (3) белых, пятнадцать (15) черных и семь (7) красных шаров. Извлекается наугад один шар. Какова вероятность того, что он не окажется черным.
2. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при ста (100) выстрелах мишень будет поражено от 75 до 90 раз.
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
1,09 |
0,24 |
1,08 |
1,43 |
0,94 |
1,99 |
2,96 |
3,09 |
1,10 |
1,34 |
1,66 |
1,80 |
1,67 |
2,46 |
0,58 |
1,53 |
1,20 |
1,01 |
2,17 |
2,75 |
2,37 |
2,09 |
1,18 |
1,38 |
0,68 |
0,91 |
2,63 |
2,16 |
2,60 |
1,46 |
2,76 |
0,76 |
0,58 |
2,16 |
1,36 |
2,90 |
2,53 |
0,97 |
1,74 |
0,58 |
1,31 |
1,87 |
2,92 |
1,65 |
1,80 |
2,54 |
1,80 |
1,27 |
1,67 |
1,14 |
Вариант № 11
1. В урне находится двенадцать (12) шаров с номерами от 1 до 12. Какова вероятность того, что на двух наугад вынутых шарах сумма номеров окажется равной десяти (10)?
2. В тире имеются 4 ружья. Вероятности попадания для стрелка из каждого ружья соответственно равны: из первого – 0,6; из второго – 0,7; из третьего – 0,8; из четвертого – 0,9.
Стрелок берет ружье наугад и дважды стреляет в цель. Какова вероятность поражения цели?
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
0,83 |
2,07 |
3,40 |
4,42 |
2,76 |
8,00 |
5,44 |
-2,27 |
3,19 |
0,51 |
||||
3,88 |
-0,12 |
1,48 |
8,70 |
7,26 |
0,14 |
3,19 |
1,85 |
0,78 |
5,71 |
||||
-1,08 |
2,65 |
0,19 |
-0,39 |
1,15 |
6,35 |
-2,43 |
4,26 |
1,96 |
7,85 |
||||
5,12 |
1,48 |
5,01 |
6,61 |
0,62 |
2,12 |
4,04 |
-3,28 |
8,16 |
8,33 |
||||
4,26 |
3,19 |
2,28 |
3,03 |
1,21 |
2,87 |
8,86 |
3,62 |
1,69 |
9,61 |
||||
Вариант № 12
1. В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 100 денежных и 300 вещевых выигрышей. Какова вероятность выигрыша по случайным образом купленному билету?
2. В урне 1 имеется 5 белых и 2 красных шара; в урне 2 – 6 белых и 1 красный шар. Из каждой урны вынимается по шару. Какова вероятность того, что вынутые шары будут одного цвета?
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
12,36 |
11,57 |
13,18 |
13,44 |
10,98 |
14,71 |
10,25 |
10,19 |
15,38 |
7,54 |
13,14 |
9,00 |
14,10 |
14,80 |
15,38 |
14,26 |
13,30 |
11,66 |
16,61 |
12,55 |
10,8 |
17,2 |
11,72 |
18,32 |
9,9 |
10,9 |
16,0 |
13,48 |
11,55 |
11,84 |
13,33 |
11,55 |
12,69 |
12,5 |
11,01 |
11,52 |
11,84 |
14,71 |
12,96 |
10,31 |
14,04 |
8,07 |
12,58 |
10,34 |
11,01 |
11,68 |
11,0 |
9,15 |
11,5 |
8,07 |
Вариант № 13
1. Монета брошена четыре раза. Найти вероятность того, что при этом герб выпадает хотя бы один раз.
2. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена не более 70 раз.
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
3,85 |
6,39 |
0,24 |
4,08 |
2,55 |
3,77 |
3,51 |
5,75 |
2,99 |
4,66 |
3,37 |
1,25 |
4,43 |
4,14 |
4,11 |
7,28 |
3,82 |
5,64 |
3,07 |
7,37 |
7,12 |
3,54 |
3,51 |
0,42 |
3,48 |
6,65 |
6,77 |
4,14 |
2,76 |
1,03 |
4,49 |
5,39 |
6,48 |
1,72 |
4,55 |
3,88 |
8,01 |
4,57 |
5,12 |
3,25 |
1,23 |
5,15 |
3,80 |
5,64 |
6,34 |
0,91 |
5,3 |
5,49 |
3,68 |
1,83 |
Вариант № 14
1. 10 министров рассаживаются случайным образом в зале заседаний за круглым столом. Какова вероятность, что при этом министр финансов окажется рядом с министром культуры?
2. Имеются две партии изделий: в первой 12 штук, во второй – 10, причем в каждой из них одно изделие бракованное. Из первой партии во вторую переложили одно наудачу взятое изделие, затем из второй партии взяли наудачу одно изделие. Какова вероятность того, что оно бракованное?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
1,81 |
1,05 |
1,81 |
3,88 |
3,98 |
3,77 |
5,26 |
1,7 |
5,41 |
1,81 |
7,08 |
1,79 |
2,53 |
1,74 |
3,37 |
3,68 |
2,02 |
4,47 |
4,07 |
6,63 |
0,68 |
2,62 |
1,41 |
5,5 |
2,01 |
5,57 |
3,93 |
2,98 |
4,4 |
5,69 |
0,05 |
0,55 |
3,86 |
2,83 |
3,37 |
2,1 |
6,18 |
4,65 |
5,42 |
0,32 |
4,86 |
3,95 |
4,72 |
3,32 |
1,49 |
3,43 |
4,67 |
3,18 |
5,48 |
2,15 |
Вариант № 15
1. Бросаются 3 игральные кости одновременно. Какова вероятность, что при этом выпадет 8 очков?
2.
Производится
850 независимых испытаний. В каждом из
них событие
может появиться с вероятностью
.
Какова вероятность того, что событие
появится в меньшинстве из произведенных
испытаний?
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
10,62 |
7,24 |
9,02 |
5,74 |
8,08 |
5,99 |
9,09 |
5,30 |
9,90 |
8,99 |
9,29 |
8,08 |
5,57 |
8,2 |
8,3 |
7,3 |
7,09 |
9,95 |
8,5 |
7,27 |
9,51 |
8,3 |
9,4 |
8,1 |
10,87 |
6,65 |
4,56 |
8,69 |
6,97 |
8,33 |
11,1 |
6,36 |
8,97 |
9,09 |
6,28 |
9,24 |
10,99 |
9,26 |
10,57 |
6,9 |
7,64 |
6,39 |
6,77 |
4,5 |
8,65 |
8,13 |
6,4 |
8,38 |
9,37 |
8,89 |
Вариант № 16
1. Ящик содержит 75 качественных деталей и 25 дефектных. Найти вероятность того, что из 4 вынутых наугад деталей половина годных.
2. Вероятность поражения цели при одном выстреле составляет 0,3. Какова вероятность того, что при 5 выстрелах цель не будет поражена?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
6,65 |
4,62 |
6,52 |
5,21 |
4,92 |
5,54 |
7,63 |
6,97 |
7,69 |
6,8 |
7,31 |
7,64 |
6,41 |
6,68 |
6,76 |
4,88 |
5,52 |
5,57 |
7,41 |
6,12 |
6,55 |
7,41 |
6,23 |
5,41 |
5,47 |
5,44 |
7,63 |
6,97 |
7,69 |
6,8 |
6,85 |
5,63 |
6,2 |
5,5 |
6,02 |
5,6 |
5,24 |
5,3 |
7,13 |
6,05 |
5,69 |
6,52 |
5,63 |
5,33 |
5,66 |
7,57 |
7,88 |
7,33 |
5,44 |
5,12 |
Вариант № 17
1. Для олимпиады отобрана группа из 30 школьников, из которых 10 являются отличниками. При рассаживании в аудитории их запускают группами по 5 человек, отбирая наугад. Какова вероятность, что в первой группе окажется четыре отличника?
2. Из трамвайного парка в случайном порядке последовательно выходят четыре трамвая маршрута № 1 и шесть трамваев маршрута № 2. Найти вероятность того, что вторым на линию выйдет трамвай № 2.
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
9,08 |
7,37 |
9,63 |
6,13 |
9,03 |
11,46 |
8,45 |
12,45 |
9,80 |
11,63 |
11,49 |
6,97 |
10,5 |
14,65 |
9,08 |
10,45 |
6,15 |
13,87 |
6,44 |
8,68 |
8,56 |
6,88 |
9,2 |
4,27 |
8,01 |
9,63 |
8,97 |
8,59 |
8,18 |
10,47 |
9,46 |
9,37 |
9,17 |
7,52 |
9,03 |
5,66 |
9,78 |
11,63 |
9,31 |
9,60 |
7,98 |
8,82 |
12,47 |
4,52 |
6,5 |
9,46 |
9,52 |
6,39 |
6,97 |
7,66 |
Вариант № 18
1. Абонент забыл две последние цифры телефонного номера, помнит только, что они были различны. Какова вероятность того, что, набирая номер наугад, он не ошибется?
2.
Опыт в котором случайное событие А может
появиться с вероятностью
,
повторяют 100 раз. Найти вероятность
того, что при этом событие А появится
от 20 до 40 раз.
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
8,17 |
11,65 |
8,49 |
6,08 |
8,67 |
11,39 |
8,59 |
8,28 |
7,28 |
7,49 |
6,45 |
9,66 |
7,41 |
5,56 |
9,30 |
6,32 |
8,88 |
7,15 |
3,75 |
9,77 |
10,58 |
9,56 |
5,63 |
10,37 |
8,07 |
6,05 |
10,27 |
8,64 |
8,83 |
6,42 |
8,09 |
10,11 |
6,55 |
11,21 |
8,36 |
9,66 |
9,66 |
9,04 |
12,2 |
9,69 |
7,39 |
7,49 |
7,88 |
7,23 |
8,93 |
7,96 |
9,35 |
6,84 |
12,23 |
7,26 |
Вариант № 19
1. Банковский сейф имеет на замке пять (5) дисков, каждый из которых допускает набор пять (5) цифр.
2. Два стрелка стреляют по мишени. Вероятность попадания при одном выстреле: для первого стрелка – 0,7; для второго стрелка – 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один стрелок.
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
4,46 |
3,14 |
4,44 |
4,98 |
4,23 |
5,88 |
7,38 |
7,59 |
4,47 |
4,85 |
5,36 |
5,57 |
5,37 |
6,61 |
3,67 |
5,15 |
4,63 |
4,34 |
6,15 |
7,06 |
6,45 |
5,90 |
4,58 |
4,92 |
3,81 |
4,18 |
6,85 |
6,13 |
6,80 |
5,02 |
7,06 |
3,93 |
3,65 |
6,13 |
4,86 |
7,28 |
6,69 |
4,26 |
5,41 |
3,67 |
4,81 |
5,67 |
7,31 |
5,32 |
5,55 |
6,71 |
5,55 |
4,72 |
5,36 |
4,53 |
Вариант № 20
1. На палитре семь цветов. Требуется закрасить пять листов альбома. Цвет может выбраться случайно. Какова вероятность, что при этом все листы окажутся окрашенными в красный цвет?
2.
Производится 400 независимых испытаний,
в каждом из которых событие А появляется
с вероятностью
.какова
вероятность, что А произойдет в большинстве
произведенных испытаний?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
4,79 |
5,30 |
5,80 |
6,17 |
5,58 |
7,44 |
6,53 |
4,19 |
5,73 |
6,28 |
6,02 |
4,55 |
5,12 |
7,29 |
7,0 |
4,64 |
5,73 |
5,25 |
4,87 |
6,62 |
4,2 |
5,54 |
4,66 |
6,74 |
5,07 |
5,8 |
4,03 |
6,11 |
5,29 |
6,58 |
6,41 |
5,12 |
6,37 |
6,9 |
4,81 |
5,35 |
6,03 |
3,43 |
7,5 |
4,38 |
6,11 |
5,73 |
5,4 |
5,67 |
6,84 |
5,61 |
7,74 |
5,88 |
5,2 |
8,01 |
Вариант № 21
1. На складе имеется 15 телевизоров, 10 из которых изготовлены на Харьковском заводе. Найти вероятность того, что из 5 взятых наудачу телевизоров 3 изготовлены в Харькове.
2. Два равных по силе шахматиста играют в шахматы. Что вероятнее для каждого из них: выиграть 3 партии из 6 или 4 партии из 8? Т.к. ничья не учитывается, то вероятности проигрыша и выигрыша равны.
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
9,7 |
11,17 |
7,73 |
10,89 |
9,92 |
10,93 |
7,82 |
8,72 |
8,5 |
9,49 |
12,16 |
8,17 |
10,25 |
6,69 |
9,33 |
8,04 |
14,16 |
11,79 |
8,19 |
14,42 |
10,5 |
11,82 |
7,18 |
10,53 |
8,38 |
9,18 |
7,06 |
7,71 |
8,23 |
8,96 |
10,19 |
6,81 |
11,08 |
6,63 |
9,09 |
12,86 |
9,08 |
12,89 |
13,35 |
10,65 |
13,26 |
10,47 |
10,22 |
7,71 |
13,78 |
6,29 |
13,83 |
6,99 |
7,24 |
7,09 |
Вариант № 22
1. Для дежурства на избирательном участке отобрана группа сотрудников учреждения, среди которых 7 мужчин и 8 женщин. При распределении их на дежурство на участок А были случайно отобраны трое. Какова вероятность того, что среди них две женщины?
2. Из колоды 52 карты переложена наугад 1 карта в колоду 36 из карт. Какова вероятность вынуть туз из второй колоды?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
7,26 |
6,47 |
6,27 |
5,12 |
8,1 |
7,26 |
7,62 |
7,18 |
8,84 |
7,11 |
6,03 |
6,14 |
6,17 |
6,93 |
7,4 |
7,45 |
7,59 |
5,64 |
6,88 |
6,03 |
7,52 |
6,96 |
6,46 |
6,35 |
6,03 |
8,23 |
6,8 |
6,45 |
7,16 |
6,01 |
7,22 |
6,78 |
6,71 |
8,37 |
7,31 |
8,6 |
6,12 |
5,23 |
7,01 |
4,57 |
7,32 |
4,42 |
7,82 |
7,55 |
7,78 |
8,11 |
5,43 |
7,27 |
8,64 |
7,31 |
Вариант № 23
1. Случайно выбранная кость домино оказалась не дублем. Какова вероятность того, что вторую случайно взятую кость можно будет приставить к первой?
2.
Аппаратура
содержит 2000 одинаковых надежных
элементов, вероятность отказа каждого
из них
.
Какова вероятность отказа аппаратуры
, если он (отказ) наступает при отказе
хотя бы одного из элементов.
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
2,27 |
4,33 |
2,45 |
1,03 |
2,56 |
4,22 |
2,52 |
2,33 |
1,74 |
1,87 |
1,25 |
3,15 |
1,82 |
0,72 |
2,93 |
1,17 |
2,62 |
1,66 |
|
3,21 |
3,69 |
3,09 |
0,77 |
3,57 |
2,2 |
1,01 |
3,51 |
2,46 |
2,67 |
1,23 |
2,22 |
3,42 |
1,3 |
4,07 |
2,38 |
3,15 |
2,73 |
4,99 |
3,17 |
3,15 |
1,8 |
1,87 |
2,1 |
1,71 |
2,72 |
2,14 |
2,97 |
1,48 |
4,67 |
1,73 |
Вариант № 24
1. Производится стрельба по вращающейся круговой мишени, разбитой на 12 круговых секторов, раскрашенных попеременно в красный ,желтый, зеленый, белый и синий цвета. Какова вероятность попадания в синий сектор?
2. В урне 1 было 5 красных и 3 белых шара, а в урне 2 было 6 красных и 3 белых шара. Из урны 1 в урну 2 наудачу переложили 1 шар, а затем из урны 2 наудачу вынули 1 шар. Он оказался белым. Какова вероятность того, что из урны 1 в урну 2 был переложен белый шар?
3.
Дискретная случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
4,86 |
5,88 |
5,08 |
3,10 |
3,95 |
6,76 |
1,94 |
4,62 |
2,0 |
3,87 |
1,6 |
5,29 |
3,34 |
3,93 |
7,91 |
6,33 |
0,29 |
7,0 |
1,22 |
3,34 |
5,69 |
4,01 |
4,76 |
7,83 |
4,84 |
6,95 |
2,8 |
4,19 |
6,05 |
1,38 |
3,04 |
6,09 |
3,34 |
4,89 |
3,66 |
5,37 |
3,36 |
6,9 |
2,96 |
1,89 |
6,25 |
8,74 |
2,48 |
3,18 |
6,28 |
7,35 |
4,08 |
5,72 |
3,82 |
6,33 |
Вариант № 25
1. В партии изделий десять (10) окрашенных и пять (5) неокрашенных изделий. В отдел технического контроля случайным образом отобрали четыре (4) изделия из партии. Какова вероятность того, что все отобранные изделия окрашены?
2. Случайно выбранная кость домино удаляется, а затем случайно выбирается вторая. Какова вероятность того, что ее можно будет приставить к первой?
3.
Дискретная
случайная величина
может принимать только два значения
и
,
причем
.
Известны вероятность
возможного значения
,
математическое ожидание
,
дисперсия
.
Найти закон распределения этой дискретной случайной величины .
4. Случайная величина задана функцией распределения . Найти плотность вероятностей, математическое ожидание и дисперсию .
5. В результате наблюдений за получена выборка объема .
а) Определить для выборки основной промежуток , количество интервалов распределения , построить распределение выборки.
б) Составить эмпирическую функцию распределения и построить ее график.
в) Построить гистограмму относительных частот и изобразить эмпирическую кривую плотности распределения.
г) Вычислить числовые характеристики выборки, являющиеся оценками параметров распределения и . Выдвинуть гипотезу о возможном нормальном законе распределения .
2,45 |
1,45 |
2,77 |
0,72 |
2,42 |
3,84 |
2,08 |
4,41 |
2,87 |
3,94 |
|
3,85 |
1,22 |
3,27 |
5,69 |
2,45 |
3,24 |
0,74 |
5,24 |
0,91 |
2,21 |
|
2,14 |
1,16 |
2,51 |
|
1,82 |
2,77 |
2,38 |
2,16 |
1,92 |
3,26 |
|
2,67 |
2,62 |
2,50 |
1,54 |
2,42 |
0,45 |
2,85 |
3,94 |
2,58 |
1,69 |
|
1,80 |
2,30 |
4,43 |
3,87 |
0,94 |
2,67 |
2,70 |
0,88 |
1,22 |
1,82 |
|
