
Варианты
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|
Тема: «Дифференциальное исчисление функции нескольких пременных»
Задание 1. Выполнить указанные действия.
Варианты
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
z=4e-2y + (2x + 4y -3) e-y -x -1. Показать,
что
|
7. |
Показать,
что
|
8. |
Показать,
что
|
9. |
|
10. |
z=y2
sin(x2
-y2).
Показать,
что
|
11. |
u=ln(x3
+y3
+z3
-3xyz).Показать,
что
|
12. |
u=
(x -y)(y -z)(z -x).
Показать, что
|
13. |
|
14. |
|
15. |
|
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|
21. |
|
22. |
|
23. |
|
24. |
|
25. |
|
26. |
|
27. |
|
28. |
|
29. |
|
30. |
|
Задание 2. Исследовать функцию на безусловный (локальный) экстремум.
Варианты
1. |
z=x3+y3-3xy; |
2. |
z=2x3+y3+5x2+y2; x<0;y<0; |
3. |
z=e2x(x+y2+2y); |
4. |
z=-x4-y4+2x2-4xy+2y2; |
5. |
.z=x3+y3+9xy; |
6. |
z=4(x-y)-x2-y2; |
7. |
z=x2+xy+y2+x-y+1; |
8. |
z=(x-1)2+2y2; |
9. |
z=x2+(y-1)2; |
10. |
z=x2+xy+y2-2x-y; |
11. |
z=x4+y4-2x2+4xy-2y2; |
12. |
z=(x-1)2-2y2; |
13. |
z=2xy-3x2-2y2+10; |
14. |
z=x3+y3-3xy; |
15. |
z=x2+2xy-4x+8y; |
16. |
z=x2y(4-x-y); x>0;y>0; |
17. |
z=xy(3-x-y); x>0;y>0; |
18. |
z=xy1/2-y2-x+6y; |
19. |
z=1+6x-x2-xy-y2; |
20. |
z=x2-xy+x+2y; |
21. |
z=x3+8y3-6xy+5; |
22. |
z=2xy-2x-4y; |
23. |
z=x2+y2+1; |
24. |
z=(x-1)2+y2; |
25. |
z=4(x-y)-x2-y2; |
26. |
z=2xy-3x2-3y2+10; |
27. |
z=2x2+3y2-x-7y; |
28. |
z=1-x+2y-6x2-y2; |
29. |
z= |
30. |
z=xy-3y2-3x2. |
Задание 3.
Найти условный экстремум функции z=ax2+by2 при cx+dy=1 двумя способами:
а) с помощью функции Лагранжа ;
б) сведением задачи к задаче о безусловном экстремуме.
Найти экстремум u=ax+by+cz при условии x2+y2+z2=k2.


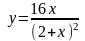








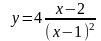

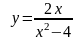



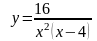
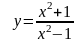





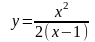





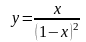

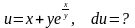

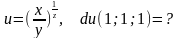
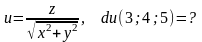

 .
.



 Найти
все частные производные первого
порядка и
Найти
все частные производные первого
порядка и .
.


 Показать,
что
Показать,
что

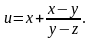 Показать,
что
Показать,
что

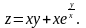 Показать,
что
Показать,
что
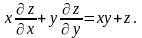
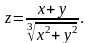 Показать,
что
Показать,
что

 Показать,
что
Показать,
что

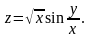 Показать,
что
Показать,
что

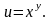 Показать,
что
Показать,
что
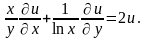
 Показать,
что
Показать,
что

 Показать,
что
Показать,
что
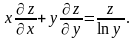
 .
Показать, что
.
Показать, что
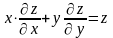
 .
Показать, что
.
Показать, что
 .
. .
Показать, что
.
Показать, что
 .
. .
Показать, что
.
Показать, что
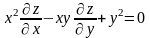 .
.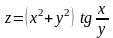 .
Показать, что
.
Показать, что
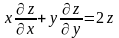 .
. .
Показать, что
.
Показать, что
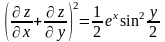 .
. .
Показать, что
.
Показать, что
 .
. .
Показать, что
.
Показать, что
 .
. .
Показать, что
.
Показать, что
 .
.