1.5 Сферический пьезокерамический преобразователь
Для проведения гидроакустических измерений необходимы излучатели и приемники звука, удовлетворяющие требованиям неискаженности звукового поля, широкого частотного диапазона, отсутствия направленности действия. Наиболее полно этим требованиям отвечают преобразователи с активным элементом сферической формы.
Пьезокерамический сферический преобразователь (рис.1) представляет собой оболочку 2 (однородную или склеенную из двух полусфер), поляризованную по толщине, с электродами на внутренней и внешней поверхностях. Вывод 3 от внутреннего электрода проходит через отверстие сальнике 1.
Р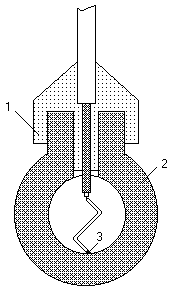
ис.1
Пьезокерамический сферический
преобразователь
Уравнение движения и эквивалентные параметры. Для составления дифференциального уравнения движения сферической оболочки выделяют квадратный элемент ее поверхности и связывают с ним прямоугольную систему координат как показано на рис. 2.
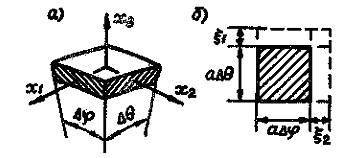
Рис.2 Элемент сферической оболочки (а) и его деформация при растяжении сферы (б)
Растяжения
или сжатия сферы вызывают деформации
ее элемента:
и механические напряжения
.
Закон Гука для выделенного элемента записывают в форме:
где
– матрица модулей гибкости.
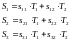
При
постоянной малости толщины
сферической оболочки по сравнению с ее
средним радиусом
пренебрегают эффектом Пуассона и
рассматривают деформации элемента
оболочки только в направлениях
,
.
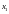в силу симметрии сферической оболочки
и ее выделенного элемента
где
- коэффициент Пуассона.
При
растяжении или сжатии сферической
оболочки ее средний радиус
изменяется на величину перемещения
,
что вызывает в оболочке деформации
Механические напряжения в сферической оболочке
Обозначим силы действующие на элемент сферической оболочки:
внешняя вынужденная сила
результирующая сила упругости
сила инерции
Дифференциальное уравнение движения тонкой сферы получается в виде
(16)
где
- масса сферической оболочки.
Тонкая
сфера как колебательная система подобно
кольцу представляет собой простейший
осциллятор с эквивалентной массой
и эквивалентной податливостью
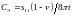
Резонансная частота колебаний сферической оболочки
Если
система координат связана с выделенным
малым элементом оболочки так, как
показано на рис. 2, то механические
граничные условия и электрические
граничные условия
определяют выбор независимых переменных
и
и запись местных уравнений пьезоэффекта
в форме
Дифференциальное уравнение движения сферического ПКЭ получают так же, как уравнение (16), составляя баланс сил, действующих на малый элемент сферической оболочки. Из всех сил, действующих на выделенный элемент, отличной будет только результирующая сил упругости:
а уравнение движении сферического ПКЭ в отличие от (2), примет вид:
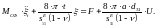
Так
как пьезоэлектрическая сила, обозначенная
в правой части уравнения, пропорциональна
напряжению:
то эквивалентная схема сферического
пьезокерамического ЭАП имеет вид:
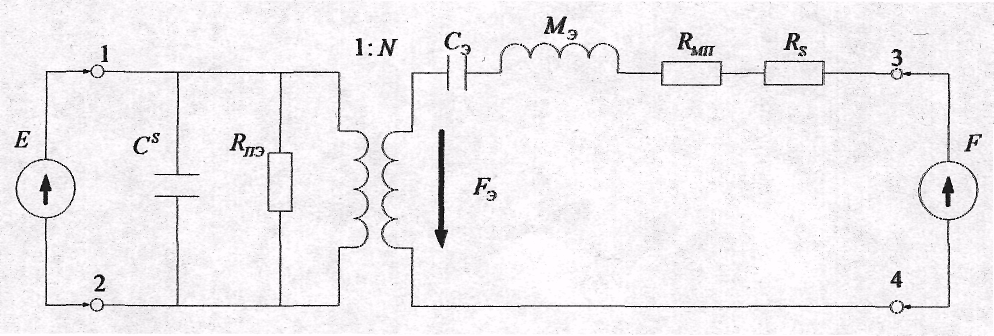
Рис.3 Эквивалентная схема сферического пьезокерамического ЭАП
В этой схеме
