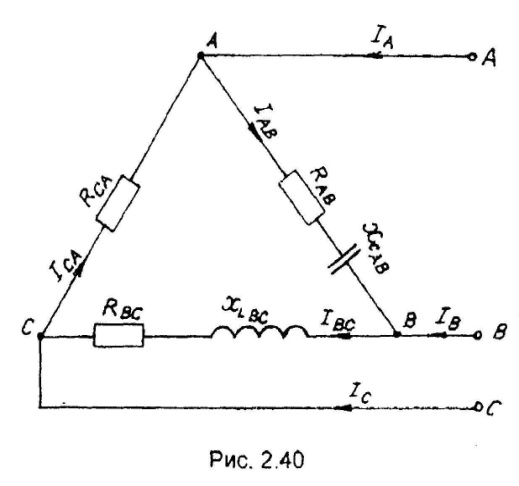
3.2.2. Методика расчета трехфазных электрических цепей переменного тока при соединении треугольником

В цепи, изображенной на схеме (рис. 3.3), потребители соединены треугольником. Известно линейное напряжение и сопротивления фаз .Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи.

Дано: , .

Определить: , , , , , ,

При соединении трехфазной цепи треугольником расчет будем вести

Рис. 3.3 символическим метолом.

1. Модули фазных напряжений при соединении треугольником равны линейным напряжениям

, то есть .

Комплексы данных напряжений запишем из условия, что вектор совмещен с действительной осью комплексной плоскости

2. Вычислим комплексы фазных сопротивлений:

где

где

где

3. Определяем фазные токи:

модуль , ;

модуль , ;

модуль , .

4. Находим линейные токи из уравнений, записанных по первому за­кону Кирхгофа для узлов В, А, С (рис. 3.3).

модуль , аргумент ;

модуль , аргумент ;

модуль , аргумент .

5. Вычисляем мощности каждой фазы и всей цепи:

,

где

,

где

,

где

где

6. Строим в масштабе векторную диаграмму напряжений и токов.

Векторы фазных токов строятся под углами к действительной оси. К концам векторов пристраиваются отрицательные фазные токи согласно уравнениям:

;

;

.

Замыкающие векторные треугольники векторов представляют в выбранном масштабе линейные токи.

Выбираем масштаб:

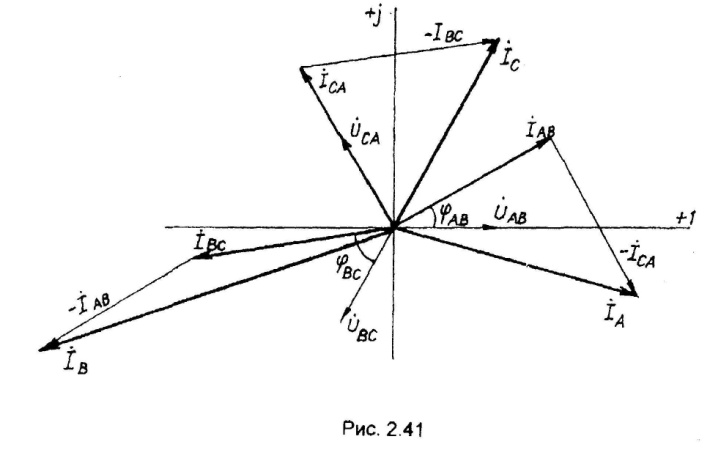
Рис. 3.4

7. Результаты расчетов занесем в соответствующие таблицы

Результаты расчета токов

Фазные и линейные токи	Алгебраическая форма, А	Показательная форма, А	Действующее значение, А