Свойства степенных рядов

Сформулируем без доказательства основные свойства степенных рядов.

1. Сумма степенного ряда (3.3) является непрерывной функцией в интервале сходимости .

2. Степенные ряды и , имеющие радиусы сходимости соответственно и , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядов не меньше, чем меньшее из числе и .

3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать. Для ряда

при

. (3.6)

4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости. Для ряда (7.3) при выполняется равенство

. (3.7)

Ряды (3.6) и (3.7) имеют тот же радиус сходимости, что и исходный степенной ряд.

Перечисленные свойства остаются справедливыми и для степенных рядов вида (3.2).

Пример 3.8. Найти сумму ряда

.

Решение. Найдем интервал сходимости данного ряда. Используя признак Даламбера, получаем

.

Для того, чтобы ряд сходился, необходимо выполнение следующего равенства:

  .

Таким образом, интервал сходимости есть .

Так как ряд сходится при , то его можно почленно дифференцировать в интервале сходимости. Обозначив сумму ряда через , имеем

.

В интервале сходимости полученный ряд есть сумма членов убывающей геометрической прогрессии со знаменателем и его сумма . Проинтегрировав ряд из производных на отрезке , где найдем сумму данного ряда:

.



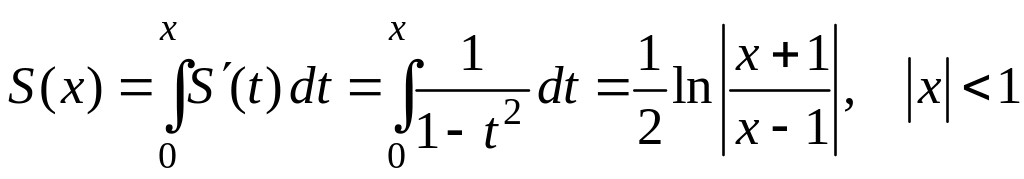3.3. Ряды Тейлора и Маклорена. Разложение функций в степенной ряд

Для приложений важно уметь данную функцию представлять в виде суммы степенного ряда.

Для любой функции , определенной в окрестности точки и имеющей в ней производные до -го порядка включительно, справедлива формула Тейлора:

,

(3.8)

где ,  остаточный член в форме Лагранжа. Причем число можно записать в виде , где .

Формулу (7.8) можно записать в виде

,

где  многочлен Тейлора.

Если функция имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки и остаточный член стремится к нулю при ( ), то из формулы Тейлора получается разложение функции по степени , называемое рядом Тейлора:

.

(3.9)

Если в ряде Тейлора положить , то получим разложение функции по степеням в так называемый ряд Маклорена:

.

(3.10)

Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки . Но отсюда еще не следует, что он будет сходиться к данной функции ; он может оказаться расходящимся или сходится, но не к функции .

В следующей теореме (которую примем без доказательства) сформулировано необходимое и достаточное условие сходимости ряда Тейлора к функции .

Теорема 3.2. Для того чтобы ряд Тейлора (3.9) функции сходился к функции в точке , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (3.8) стремился к нулю при , т.е. чтобы .

Для разложения функции в ряд Маклорена (3.10) нужно:

1. найти производные ;

2. вычислить значения производных в точке ;

3. выписать ряд (3.10) для заданной функции и найти его интервал сходимости;

4. найти интервал , в котором остаточный член ряда Маклорена при . Если такой интервал существует, то в нем функция и сумма ряда Маклорена совпадают.

Пример 3.9. Разложит в ряд Маклорена функцию и найти область, в которой ряд сходится к данной функции.

Напомним: , .

Решение. Находим производные функции :

, , , … .

Таким образом, , если  четное, и , если  нечетное.

Полагая , получаем , , , , …, , если  четное, и , если  нечетное. Подставим найденные производные в ряд (3.10). Имеем

. ()

Остаточный член в форме Лагранжа имеет следующий вид:

если  четное, то

,

где при и ;

если  нечетное, то

,

где при и .

Так как , то и . Значит,

.

при любом . Следовательно, при любом и . Значит, ряд () сходится к функции на всей числовой прямой.



Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций:

1. , при ;

2. , при ;

3. , при ;

4. , при ;

5. , при ;

6. ,

при ;

7. , при ;

8. , при .

Пример 3.10. Разложить в степенной ряд функцию .

Решение. При разложении в степенной ряд функции в формулу разложения функции вместо поставляем . Тогда получаем

.

Полученный ряд сходится при любых . Но следует помнить, что функция не определена при . Поэтому найденный ряд сходится к функции только в полуинтервале .

