Интервал и радиус сходимости
Их теоремы Абеля следует, что если
есть точка сходимости степенного ряда,
то интервал
весь состоит их точек сходимости данного
ряда; при всех значениях
вне этого интервала ряд (3.3) расходится.
Пусть
.
Интервал
или
называют интервалом сходимости.
Число
называют радиусом сходимости
степенного ряда. Таким образом,
это такое число,
что при всех
,
для которых
,
ряд (3.3) абсолютно сходится, а при
ряд расходится (см. рисунок).
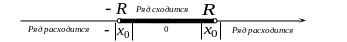
Отметим, что на концах интервала
сходимости (т.е. при
и при
)
сходимость ряда проверяется в каждом
случае отдельно.
В частности, когда ряд (3.3) сходится лишь
в одной точке
,
то считаем, что
.
Если же ряд (3.3) сходится при всех значениях
(т.е. во всех точках числовой оси), то
считаем, что
.
Для нахождения радиуса сходимости степенного ряда (3.3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда
и применим к нему признак Даламбера. Допустим, что существует предел
.
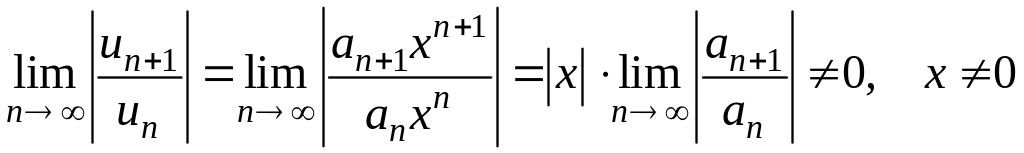По признаку Даламбера ряд сходится,
если
,
т.е. ряд сходится при тех значениях
,
для которых
.
Ряд, составленный из модулей членов
ряда (3.3), расходится при тех значениях
,
для которых
.
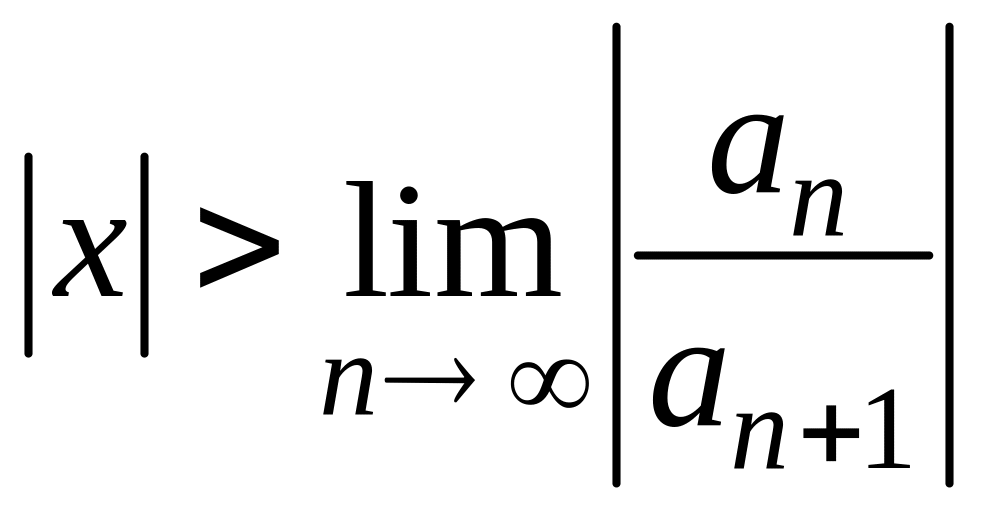Таким образом, для ряда (3.3) радиус сходимости
.
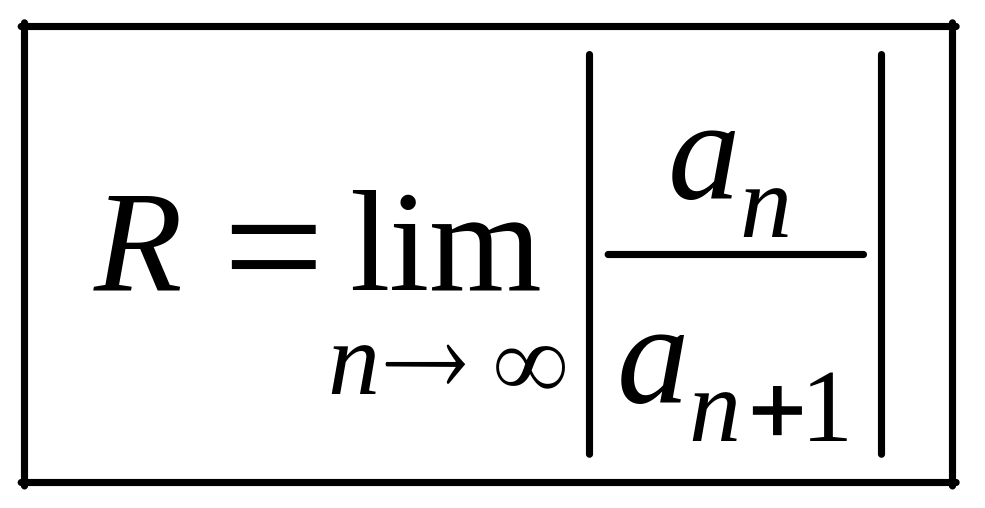(3.4)
Аналогично, воспользовавшись радикальным признаком Коши, можно получить, что
.
(3.5)
Замечания.
Если
,
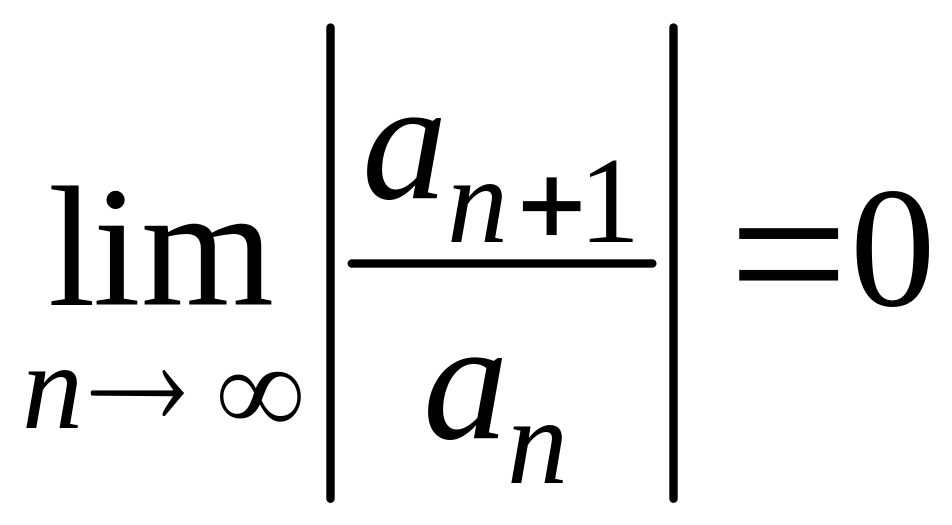то ряд (3.3) абсолютно сходится на всей
числовой оси. В этом случае
.
Если
,
то
.Если дан степенной ряд (3.2), то его радиус сходимости определяется также по формулам (3.4) или (3.5), а интервал сходимости будет интервал с центром в точке :
.
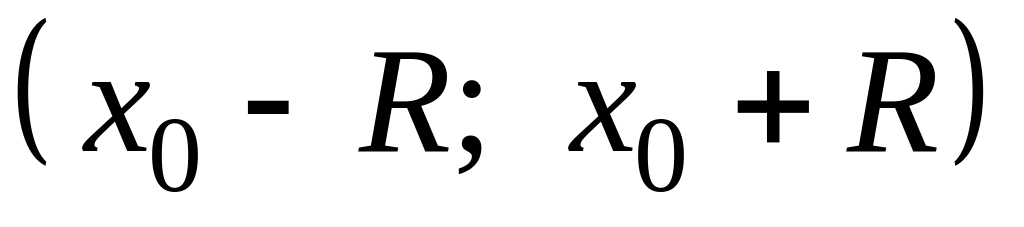Пример 3.3. Найти интервал сходимости
степенного ряда
.
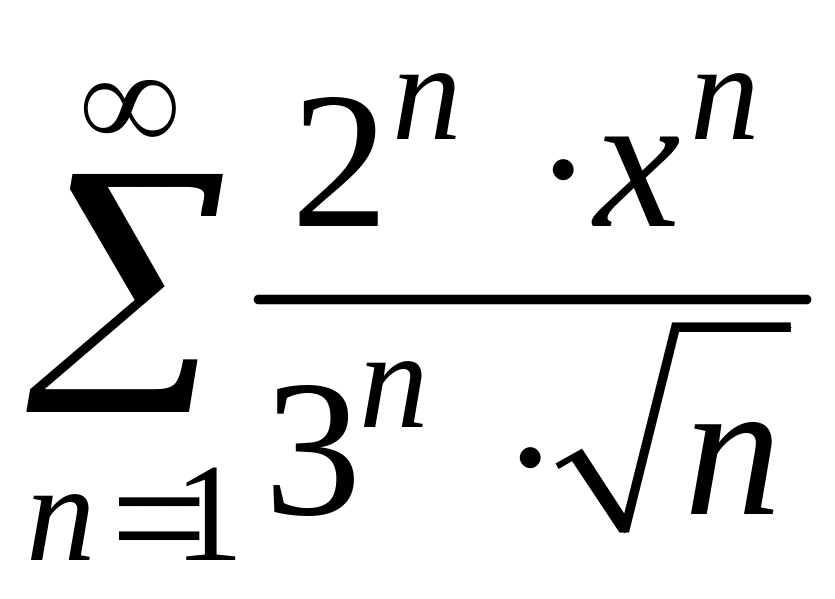Решение. I способ.
Чтобы найти радиус сходимости воспользуемся формулой (3.4). По условию
и
.
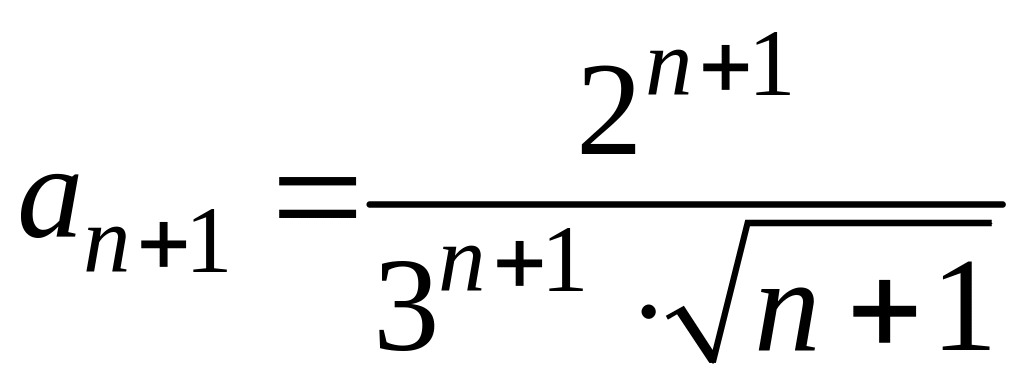Тогда
.
Таким образом, интервал сходимости
имеет вид
.
II способ.
Чтобы найти интервал сходимости степенного ряда воспользуемся признаком Даламбера:
и
.
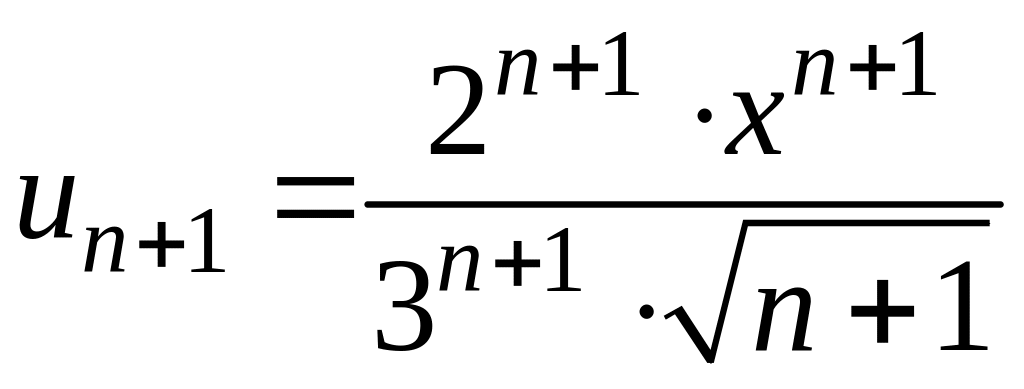Тогда
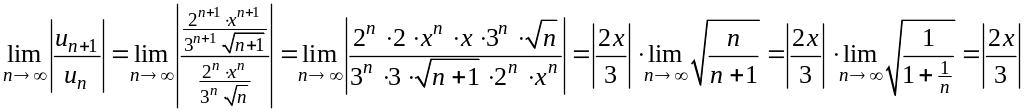
Ряд сходится по признаку Даламбера,
если
.
Тогда
.
Таким образом, интервал сходимости имеет вид .
Пример 3.4. Найти область сходимости степенного ряда .
Решение. 1. Находим интервал сходимости ряда.
Из примера 3.3. имеем следующий интервал сходимости .
2. Исследуем сходимость ряда на концах интервала.
1) При
данный ряд примет вид
.
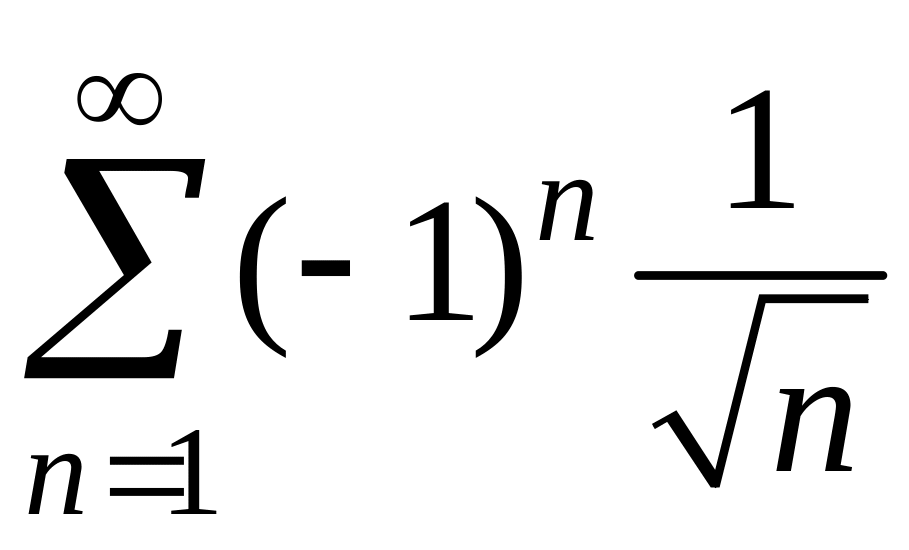Данный ряд является знакочередующимся рядом. Для исследования на сходимость используем признак Лейбница.
а)
выполняется;
б)
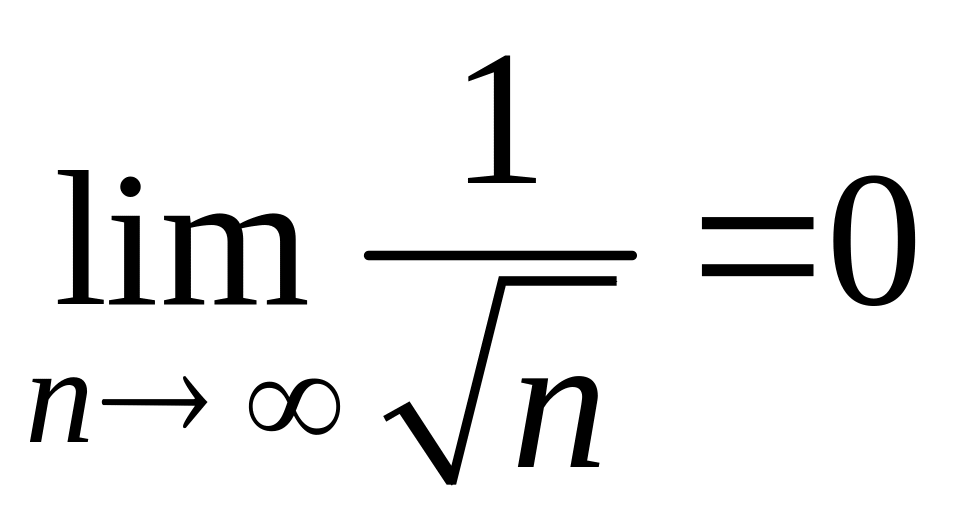выполняется
Значит, знакочередующийся ряд сходится по признаку Лейбница. Поэтому точку включаем в область сходимости.
2) При
данный ряд примет вид
.
Это числовой ряд с положительными
членами. Он расходится как ряд Дирихле
при
.
Поэтому точку
не включаем в область сходимости.
Следовательно, область сходимости
исходного степенного ряда является
полуинтервал
.
Пример 3.5. Найти область сходимости
степенного ряда
.
Решение. 1. Находим интервал сходимости ряда.
I способ.
Чтобы найти радиус сходимости воспользуемся формулой (3.5). По условию
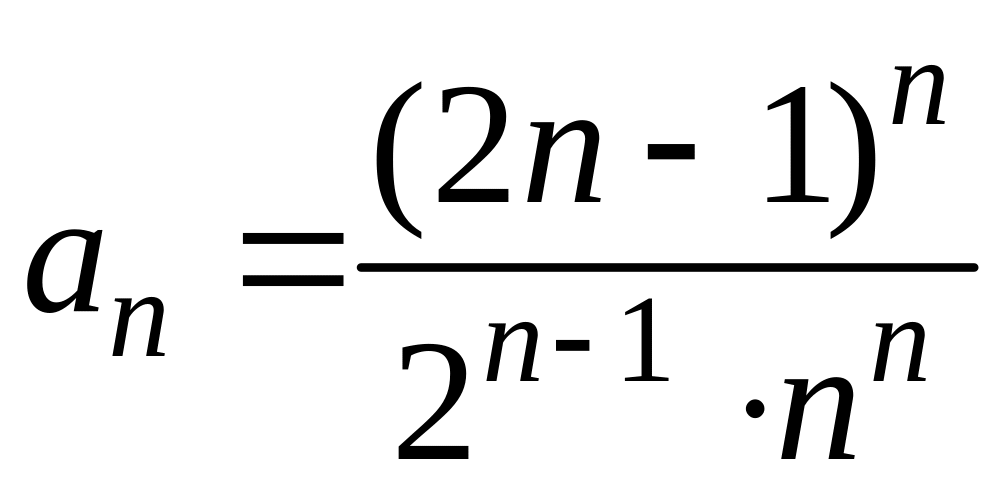и
.
Тогда
.
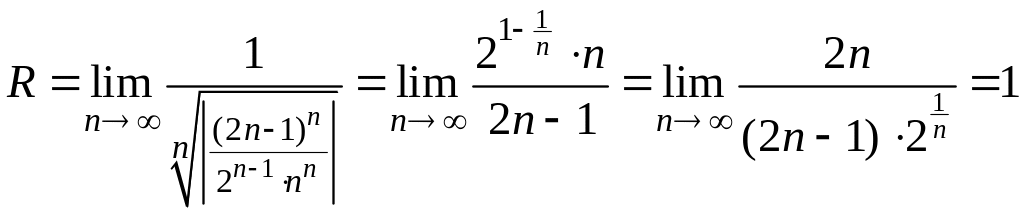Таким образом, интервал сходимости
имеет вид
.
II способ.
Чтобы найти интервал сходимости степенного ряда воспользуемся радикальным признаком Коши:
.
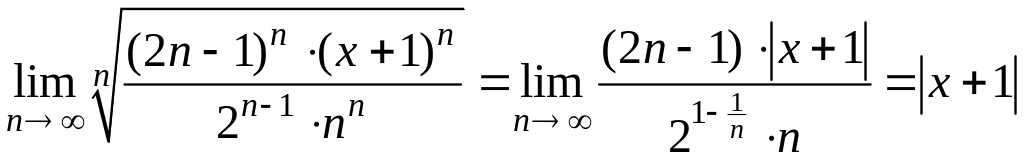По радикальному признаку Коши ряд
сходится, если
.
Тогда
.
Таким образом, интервал сходимости
имеет вид
.
2. Исследуем сходимость ряда на концах интервала.
1) При
данный ряд примет вид
.
Данный ряд является знакочередующимся рядом. Для исследования на сходимость используем признак Лейбница.
а)
не выполняется;
Значит, знакочередующийся ряд расходится по признаку Лейбница. Поэтому точку не включаем в область сходимости.
2) При
данный ряд примет вид
.
Это числовой ряд с положительными
членами. Радикальный
признак Коши не подходит, так как
.
Воспользуемся достаточным признаком
расходимости ряда.
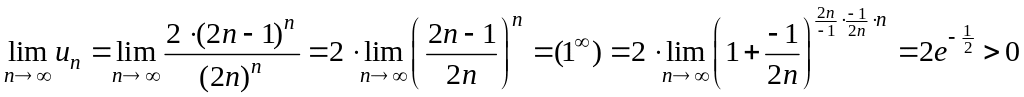
Ряд расходится. Поэтому точку не включаем в область сходимости.
Следовательно, область сходимости исходного степенного ряда совпадает с интервалом сходимости .
Пример 3.6. Найти область сходимости
степенного ряда
.
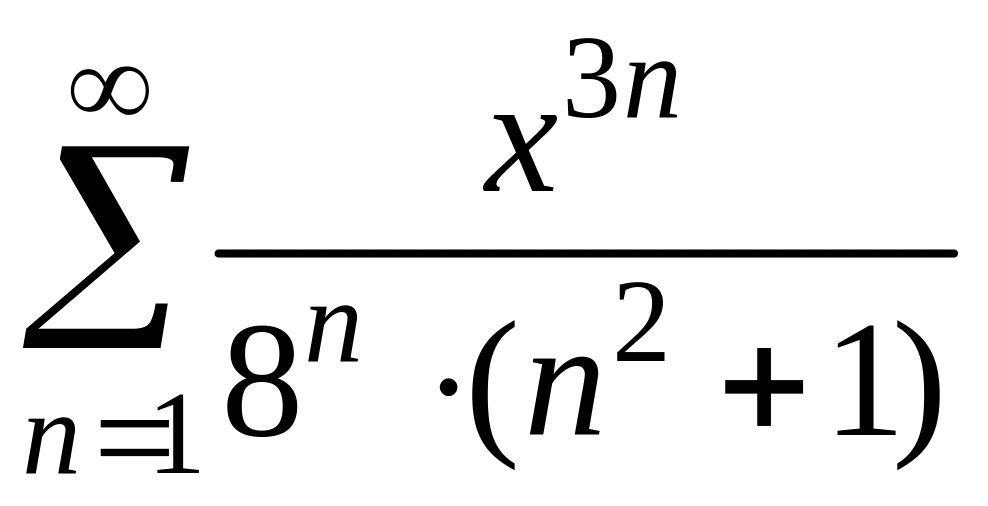Решение. 1. Находим интервал сходимости ряда.
Чтобы найти интервал сходимости степенного ряда воспользуемся признаком Даламбера:
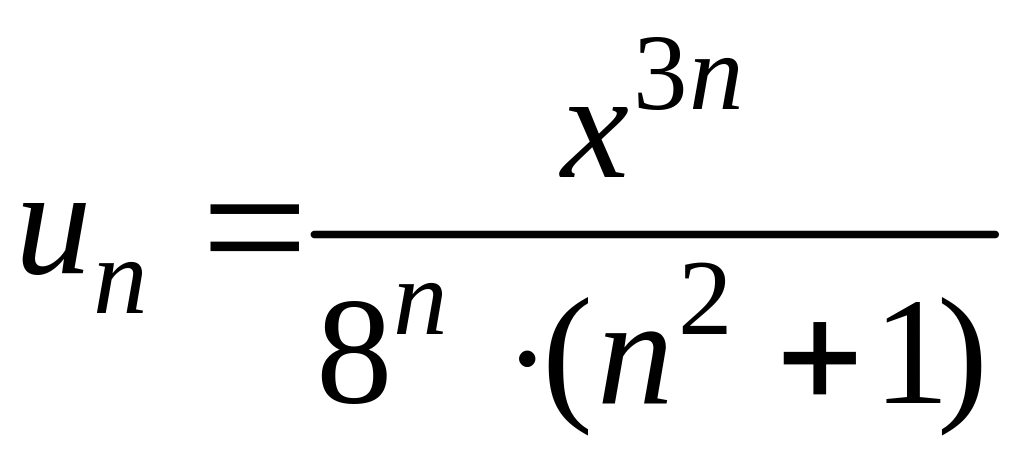и
,
.
По признаку Даламбера
.
Тогда
.
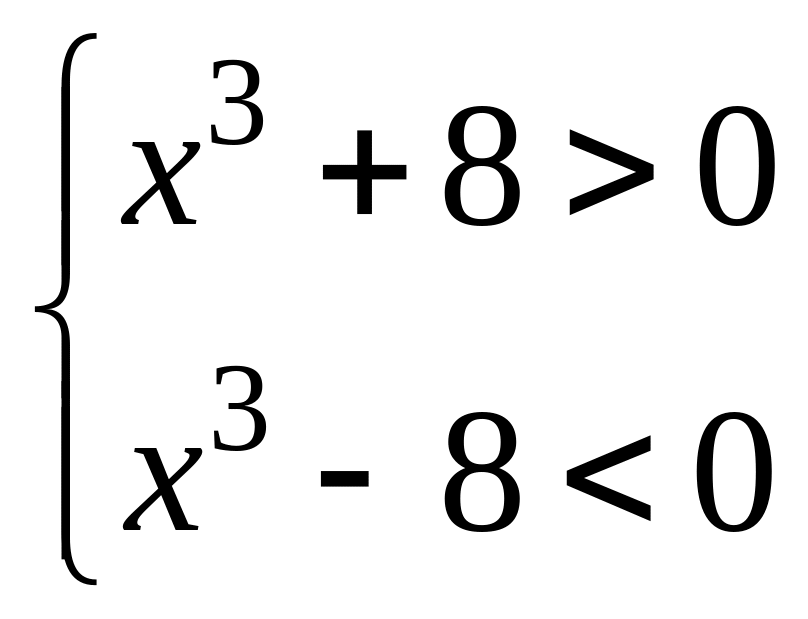
Таким образом, интервал сходимости
имеет вид
.
2. Исследуем сходимость ряда на концах интервала.
1) При данный ряд примет вид
.
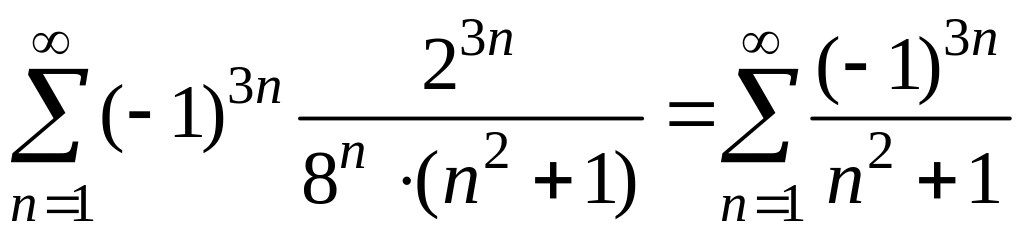Данный ряд является знакочередующимся рядом. По признаку Лейбница он сходится. Поэтому точку включаем в область сходимости.
2) При
данный ряд примет вид
.
Это числовой ряд с положительными
членами. Воспользуемся интегральным
признаком Коши. Рассмотрим функцию
,
которая непрерывна и монотонно убывает
на промежутке
.
Тогда
.
Несобственный интеграл сходится. Значит, и ряд сходится. Поэтому точку включаем в область сходимости.
Следовательно, область сходимости
исходного степенного ряда имеет вид
.
Пример 3.7. Найти область сходимости
степенного ряда
.
Решение. Находим радиус сходимости по формуле (3.4):
и
.
Тогда
.
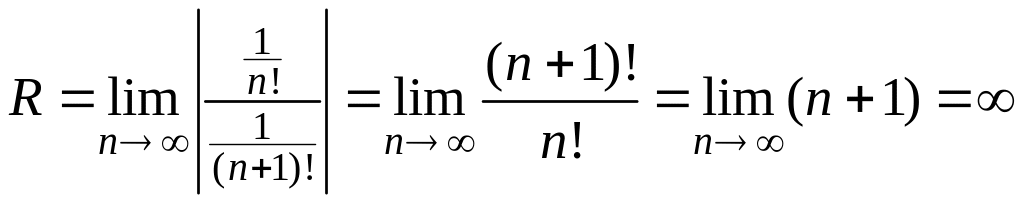Следовательно, данный ряд абсолютно сходится на всей числовой оси.