4.5. Разложение в ряд Фурье функций произвольного периода

Разлагать в ряд Фурье можно и периодические функции с периодом отличным от .

Пусть функция , определенная на отрезке , имеет период ( , где  произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.

Сделав подстановку , данную функцию преобразуем в функцию , которая определена на отрезке и имеет период . Действительно, если , то ; если , то и при имеем .

Разложение функции в ряд Фурье на отрезке имеет вид:

,

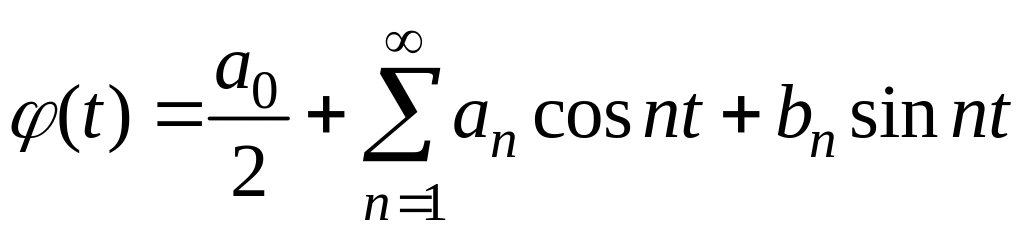где

.

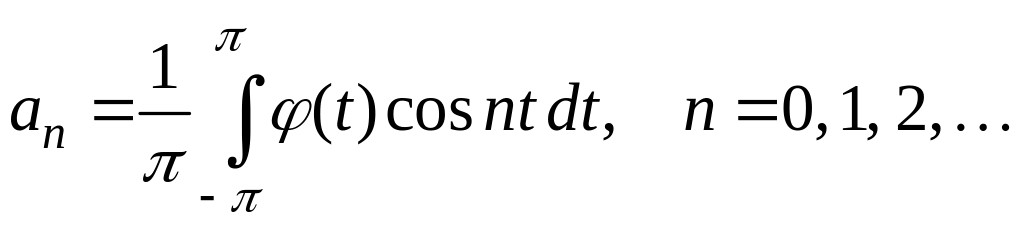
Возвращаясь к переменной и заметив, что , , получим

, (4.10)

где

(4.11)

.

Ряд (4.10) с коэффициентами, вычисляемыми по формулам (4.11), называется рядом Фурье для функции с периодом .

Все теоремы, имеющие место для рядов Фурье периодических функций, остаются в силе и для рядов Фурье функций, период которых .

В частности, если функция на отрезке четная, то ее ряд Фурье имеет вид:

, (4.12)

где , , ;

если функция  нечетная, то ряд Фурье имеет вид:

, (4.13)

где , .