35

Раздел 3

ЧИСЛОВЫЕ И ФУНКЦИОННАЛЬНЫЕ РЯДЫ

1. Числовые ряды

1.1. Основные понятия

Бесконечные ряды широко используются в теоретических исследованиях математического анализа, имеют разнообразные практические применения.

Определение 1.1. Числовым рядом (или просто рядом) называется выражение вида

, (1.1)

где  члены ряда (действительные или комплексные числа), число  общий член ряда.

Ряд считается заданным, если известно правило, по которому для любого номера можно записать соответствующий член ряда: , т.е. при помощи формулы -го члена.

Если формула дана, то можно сразу написать любой член ряда. Например, если , то ряд имеет вид: . Если ( ), то ряд имеет вид: .

Иногда ряд задается при помощи рекуррентного соотношения, связывающего последующий член ряда с предыдущим. При этом задается несколько первых членов ряда и формула, по которой находятся следующие члены ряда. Например, пусть , а рекуррентная формула такова: . Последовательно находим ; и т.д. Таким образом, получаем ряд: .

Определение 1.2. Сумма конечного числа первых членов ряда называется -й частичной суммой ряда:

.

Рассмотрим частичные суммы

,

,

………………….

Если существует конечный предел , то этот предел называют суммой ряда (1.1) и говорят, что ряд сходится. Если не существует или , то ряд (1.1) расходится и суммы не имеет. Например, ряд сходится и его сумма равна 0; ряд расходится, так как при ; ряд расходится, так как последовательность частичных сумм не имеет предела.

Пример 1.1. Дан ряд 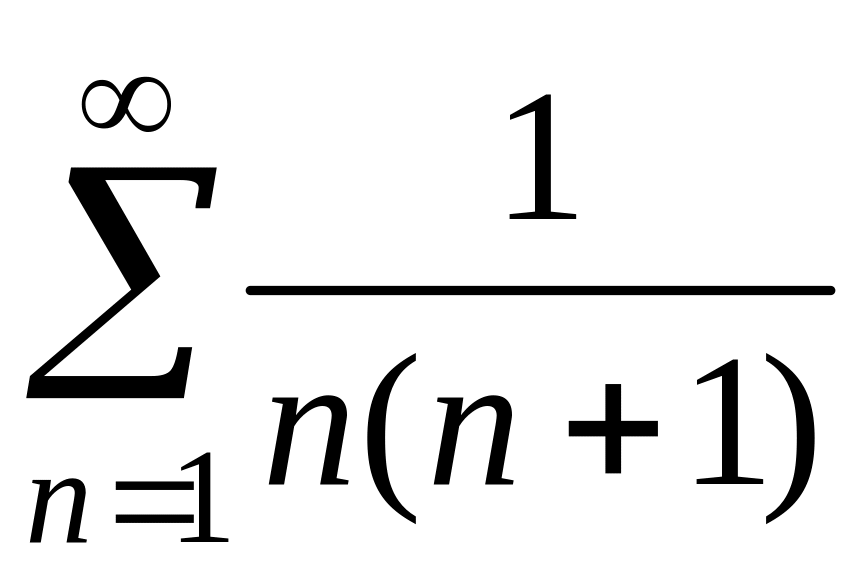. Установить сходимость этого ряда и найти его сумму.

Решение. Запишем -ю частичную сумму данного ряда и преобразуем ее:

.

Поскольку

,

то данный ряд сходится и его сумма .



Пример 1.2. Исследовать сходимость ряда

, (1.2)

который называется геометрической прогрессией.

Решение. Сумма первых членов прогрессии находится по формуле

или

.

1) Если , то при , следовательно

.

Значит, в случае ряд (1.2) сходится и его сумма .

2) Если , то при . Поэтому . А значит, в случае ряд (1.2) расходится.

3) Если , то ряд (1.2) имеет следующий вид: . В этом случае , следовательно , т.е ряд расходится.

4) Если , то ряд (1.2) имеет вид: . В этом случае

.

Следовательно, предела не имеет – ряд расходится.

Итак, ряд геометрической прогрессии сходится при и расходится при .



Рассмотрим некоторые важные свойства рядов (без доказательства).

1. Если ряд (1.1) сходится и его сумма равна , то ряд

, (1.3)

где  произвольное число, также сходится и его сумма равна . Если же ряд (1.1) расходится и , то и ряд (1.3) расходится.

2. Если ряды

и

сходятся и их суммы соответственно равны и , то ряды

(1.4)

и

(1.5)

также сходятся и их суммы соответственно равны и .

3. Если к ряду (1.1) прибавить (или отбросить) конечное число членов, то полученный ряд и ряд (1.1) сходится или расходится одновременно.

Рассмотрим сходящийся ряд (1.1)

.

Разность между суммой ряда и его -й частичной суммой называется -м остатком ряда. Остаток ряда есть в свою очередь сумма бесконечного ряда. Обозначим остаток ряда . Тогда имеем

. (1.6)

Если ряд (1.1) сходится, то .