Министерство образования Российской федерации
Тольяттинский Государственный Университет
Кафедра «Высшая математика и математическое моделирование»
Калукова О.М.
Кошелева Н.Н.
Никитина М.Г.
Павлова Е.С.
ИНдивидуальные домашние задания для студентов
Тольятти 2005
Содержание
Модуль №1«Линейная алгебра» |
3 |
Модуль №2«Векторная алгебра» |
28 |
Модуль №3 «Аналитическая геометрия» |
53 |
Модуль №4 «Введение в анализ» |
103 |
|
|
Модуль №1 Линейная алгебра
Вариант 1
Найти матрицу 3A+2B-4C, если
А=
;
В=
;
С=
Найти значение матричного многочлена
A2
+2A+3E
,
если A
=
;
Е=
Найти произведение матриц AB и BA, если
А=
;
В=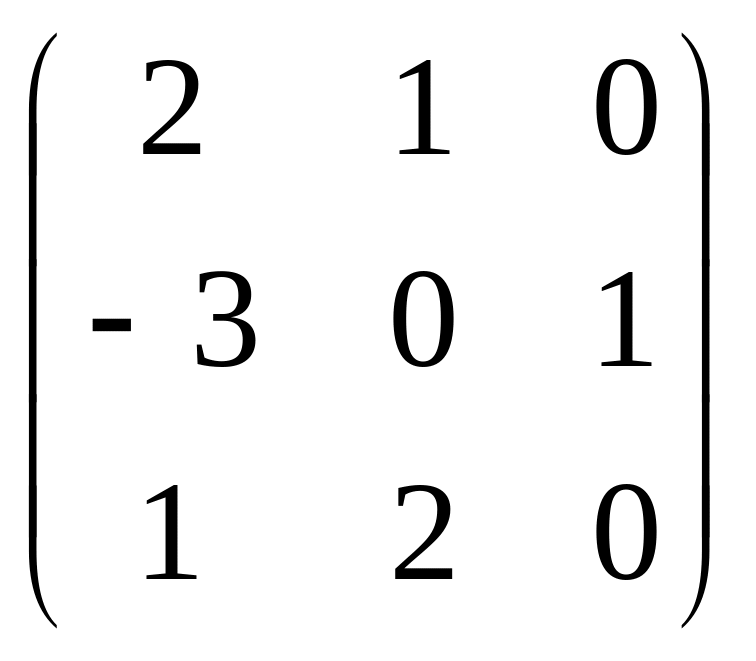
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 5 X1 – X2 +3 X3 X1 = 2 X1 +X3
X2 = X1 – 2X2 X2 = X2 -5X3
X
3
= 7X2
–
X3
X3
=
2 X1
5. Вычислить определители
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 – X2 – 6X3 = -1
X1 – 2 X2 –4X3 = 5
X1 - X2 + 2X3 = -8
Найти ранг матриц
А=
;
В=
Р ешить системы уравнений
2X1 + 5X2+ X3 +3X4 =0 2X1 +X2 =5
4X1 +6 X2 +3X3 +5X4 =0 X1+3X3=16
4 X1 +14X2 +X3 +7X4=0 5X2 –X3 =10
Вариант 2
Найти матрицу 5A-6B+2C, если
А=
;
В=
;
С=
Найти значение матричного многочлена
2A2
+3A+6E
, если
А=
;
Е=
Найти произведение матриц AB и BA, если
А=
;
В=
Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = X1 +2 X2 +2 X3 X1 = 3 X1 +X2
X2 = -3X2 +X3 X2 = X1 -2X2-X3
X 3 = 2 X1 +3 X3 X3 = 3 X1 +2X3
5. Вычислить определители
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 – 2 X2 + X3 = 6
X1 + 6 X2 +3X3 = 3
2 X1 +3 X2 +X3 = 0
7. Найти ранг матриц
А=
;
В=
8. Решить системы уравнений
3X1 + 2X2+ 5X3 +4X4 =0 3X1 -2X2 =2
2X1 +3 X2 +6X3 +8X4 =0 X1+4X3=10
X1 -6X2 -9X3 -20X4=0 6X2 –3X3 =6
Вариант 3
1.Найти матрицу 5A+6B-7C, если
А=
,
В=
,
С=
Найти значение матричного многочлена 3А2 +4A+7E, если
А=
,
Е=
3. Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 5X1 - X2 +3 X3 X1 = 2 X1 + X3
X2 = X1 –2X2 X2 = X2 -5X3
X 3 = 7 X2 - X3 X3 = 2 X1
5. Вычислить определители
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 – 3 X2 + 3X3 = 3
6 X1 + 9X2 -2X3 = -4
10 X1 +3 X2 -3X3 = 3
Найти ранг матриц
А=
;
В=
Р ешить системы уравнений
7X1 - 3X2+ 7X3 +17X4 =0 5X1 -2X2 =3
8X1 -6 X2 -X3 -5X4 =0 7X2+4X3=11
4 X1 -2X2 +3X3 +7X4=0 2X1 +5X3 =7
Вариант 4
Найти матрицу 2A+6B-5C, если
А=
,
В=
,
С=
Найти значение матричного многочлена
5A2
+3A+8E
, если
A =
,
Е=
Найти произведение матриц AB и BA, если
А=
,
В=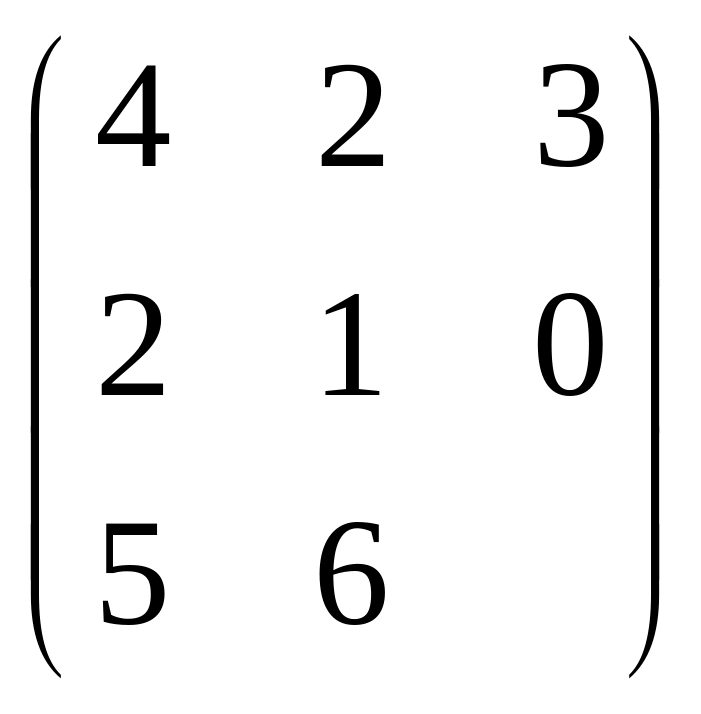
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 4X1 +3X2 +5 X3 X1 = 4 X1 +5X2-3X3
X2 = 6X1 +7X2 + X3 X2 = X1 -X2-X3
X 3 = 9X1 +X2 +8 X3 X3 = 7 X1 +4X2
5. Вычислить определители
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
X 1 + X2 -6X3 = 6
3 X1 - X2 -6 X3 = 2
2X1 +3 X2 +9X3 = 6
Найти ранг матриц
А=
;
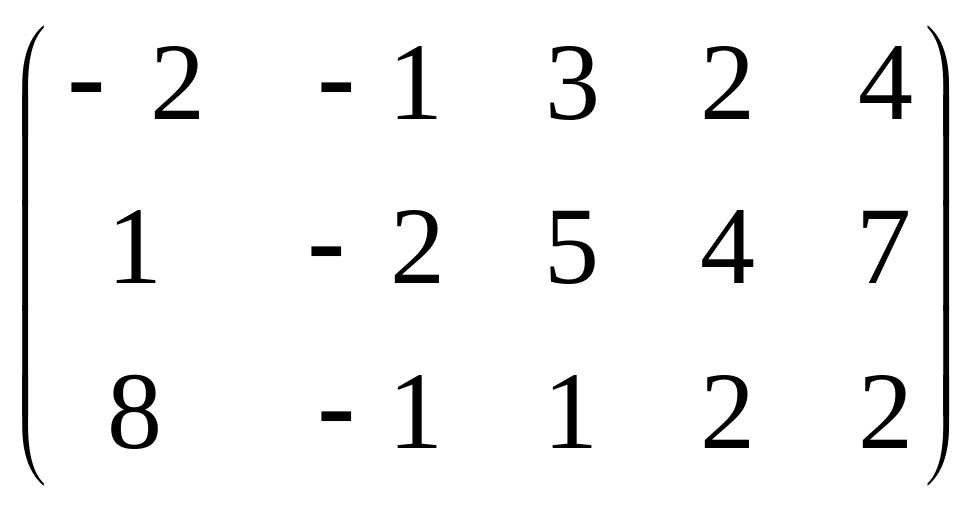В=
Решить системы уравнений
7
X1
- 3X2+
7X3
+17X4
=0 2X1
+2X2
=4
8X1 -6 X2 -X3 -5X4 =0 3 X1 -2X3=1
4 X1 -2X2 +3X3 +7X4=0 X1 +2X2 +3X3 =6
Вариант 5
Найти матрицу 5A+7B-8C, если
А=
,
В=
,
С=
Найти значение матричного многочлена
2A2
+3A-7E
, если А=
,
Е=
Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 4X1 +3X2 +5 X3 X1 = -X1 +5X2-3X3
X2 = 6X1 +7X2 + X3 X2 = X1 -X2-X3
X 3 = 9X1 +X2 +8 X3 X3 = 7 X1 -4 X3
5. Вычислить определители
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
4 X1 -3 X2 +X3 = 7
X1 - 2X2 -2X3 = 3
3 X1 - X2 +2X3 = -1
7. Найти ранг матриц
А=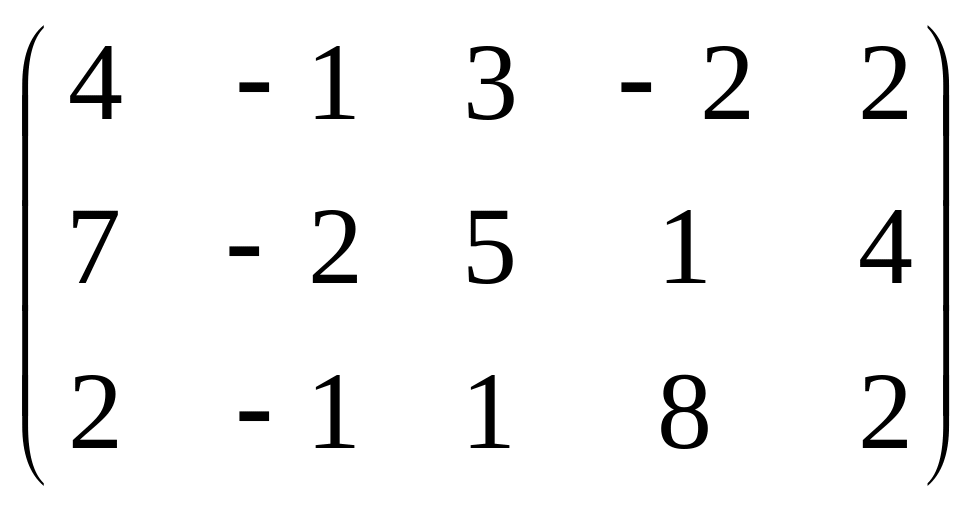
,
В=
8. Решить системы уравнений
5 X1 +11X2+ 3X3 +2X4 =0 5X1 +3X2 =8
2X1 +5 X2 +X3 +X4 =0 X1-X2 +2X3=0
X 1 -7X2 -X3 +2X4=0 3X2 +X3 =4
Вариант 6
Найти матрицу 6A-2B+4C, если
А=
,
В=
,
С=
Найти значение матричного многочлена
2A2
-7A+3E
, если
А=
,
Е=
Найти произведение матриц AB и BA, если
А=
,
В =
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 3X2 +5 X3 X1 = 2 X1 -X2-5X3
X2 = X1 +X2 + X3 X2 = 7X1 +X2+4X3
X 3 = 3X2 -6 X3 X3 = 6 X1 +4X2-7X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
6 X1 +5 X2 -2X3 = -4
3X1 +4X2 +2X3 = 1
3 X1 - 9 X2 =11
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
2 X1 +X2+ 7X3 +3X4 =0 4X1+2X2 +X3=7
4X1 +2 X2 +3X3 +2X4 =0 X1-X2 +X3=1
4 X1 +2X2 +X3 +2X4=0 X1+X2 +X3=3
Вариант 7
Найти матрицу 5A-3B+4C, если
А=
,
В=
,
С=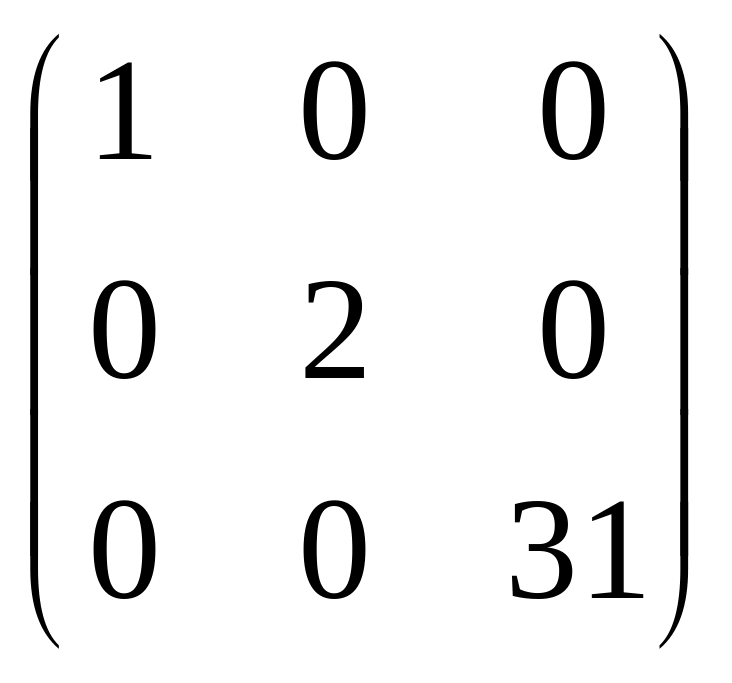
Найти значение матричного многочлена
2A2 +A-5E , если А= , Е==
3. Найти произведение матриц AB и BA, если
А==
,
В==
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 4X1+3X2 +2 X3 X1 = X1 -2X2-X3
X2 = -2X1 +X2 - X3 X2 = 3X1 +X2+2X3
X 3 = 3X1 +X2 + X3 X3 = X1 +2X2+2X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 + X2 + 4X3 = -1
X1 +3X2 -6X3 = 3
3 X1 - 2 X2 +2X3 =8
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
4 X1 +2X2+ 3X3 +X4 =0 3X1+4X2 =7
3X1 +5 X2 +X3 +X4 =0 X1+2X2 +3X3=6
7 X1 +4X2 +5X3 +2X4=0 X1-X2 +X3=1
Вариант 8
Найти матрицу 8A-7B+2C, если
А=
,
В=
,
С=
2. Найти значение матричного многочлена
5A2
-3A+4E
, если A
=
,
E=
3. Найти произведение матриц AB и BA, если
А==
,
В==
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 2X2 X1 = -3X1 +X3
X2 = -2X1 +3X2 +2 X3 X2 = 2X2+X3
X 3 = 4 X1 -X2 +5 X3 X3 = -X2+3X3
5. Вычислить определители
;
;
;
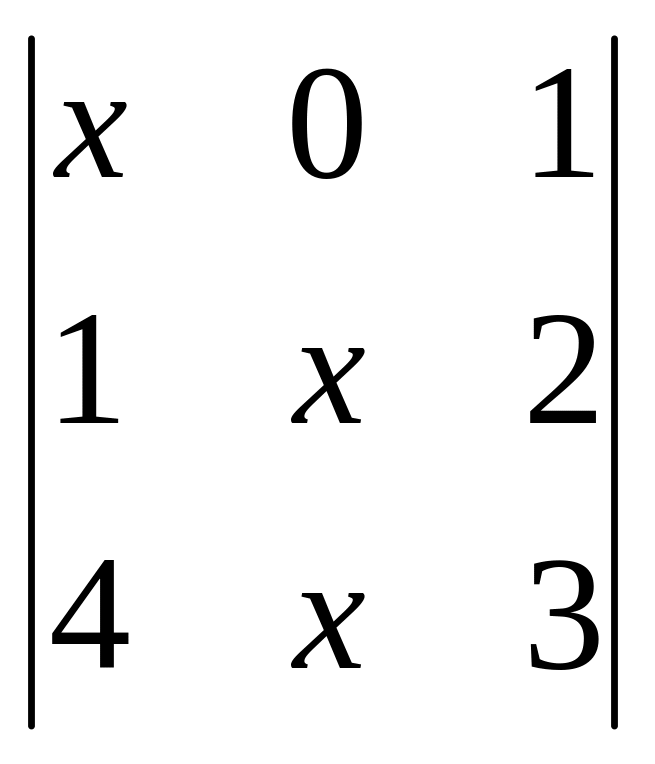6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
6 X1 + 8X2 +X3 = -8
3X1 +4X2 +X3 = -3
3 X1 +5 X2 +3X3 =-6
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
3 X1 +2X2+ 4X3 +X4 =0 5X1+4X2 -2X3=7
3X1 +2 X2 -2X3 +X4 =0 X1+2X2 -3X3=0
9 X1 +6X2 +X3 +3X4=0 X1+X2 -3X3=-1
Вариант 9
Найти матрицу 5A-6B+7C, если
A=
,
В=
,
С=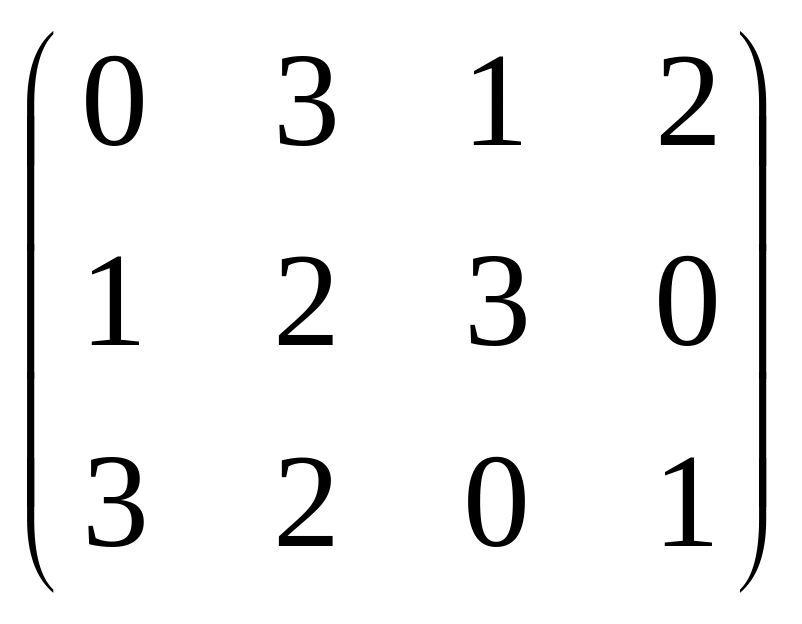
2. Найти значение матричного многочлена
5A2
-6А+7Е,
если A=
,
E==
3. Найти произведение матриц AB и BA, если
А=
,
В==
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 7X1 +3X2 +4 X3 X1 = X1+ X2-6X3
X2 = 4X2 -9 X3 X2 = 3X1+7X3
X 3 = 3X1 +X2 + X3 X3 = X1+ X2-X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 + 5X2 +4X3 = 20
X1 +3X2 +2X3 = 11
2X1 +10X2 +9X3 =40
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
4 X1 -2X2+ X3 +X4 =0 4X1+2X2 +5X3=11
6X1 -3 X2 +4X3 +8X4 =0 2X1-X2 +X3=2
6 X1 -3X2 +2X3 +4X4=0 X1-X2 +X3=1
Вариант 10
Найти матрицу 8A+2B-5C, если
А=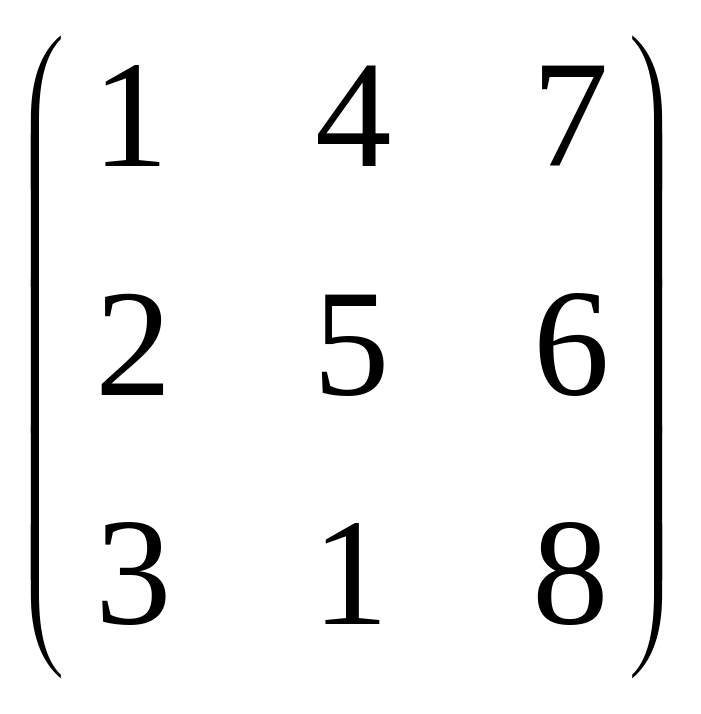
,
В=
,
С=
2. Найти значение матричного многочлена
42 +5A-6E , если А= , E==
3. Найти произведение матриц AB и BA, если
А= , В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 7X1+4 X3 X1 = X2-6X3
X2 = 4X2 -9 X3 X2 = 3X1+7X3
X 3 = 3X1 +X2 X3 = X1+ X2-X3
5. Вычислить определители
;
;
;
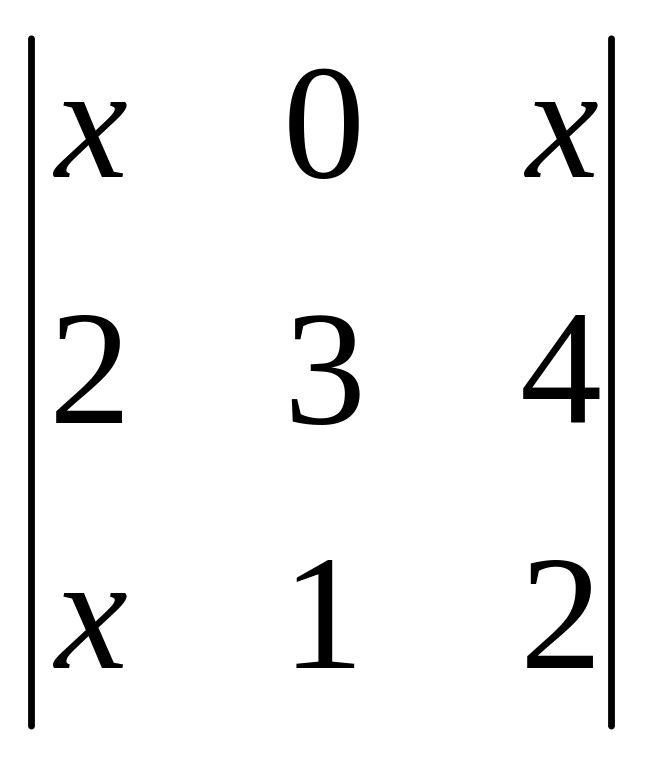6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 + 3Х2 +11X3 = 2
X1 + X2 +5X3 = 1
2 X1 + X2 +3X3 =-3
7. Найти
ранг матриц А=
,
В=
8. Решить системы уравнений
2 X1 +2X2+ 8X3 -3X4 =0 5X1+2X2 +3X3=10
3X1 +3 X2 +5X3 -2X4 =0 X1-X2 +2X3=0
2 X1 +2X2 +4X3 -X4=0 X1+X2 +X3=3
Вариант 11
Найти матрицу 2A+7B-5C, если
A=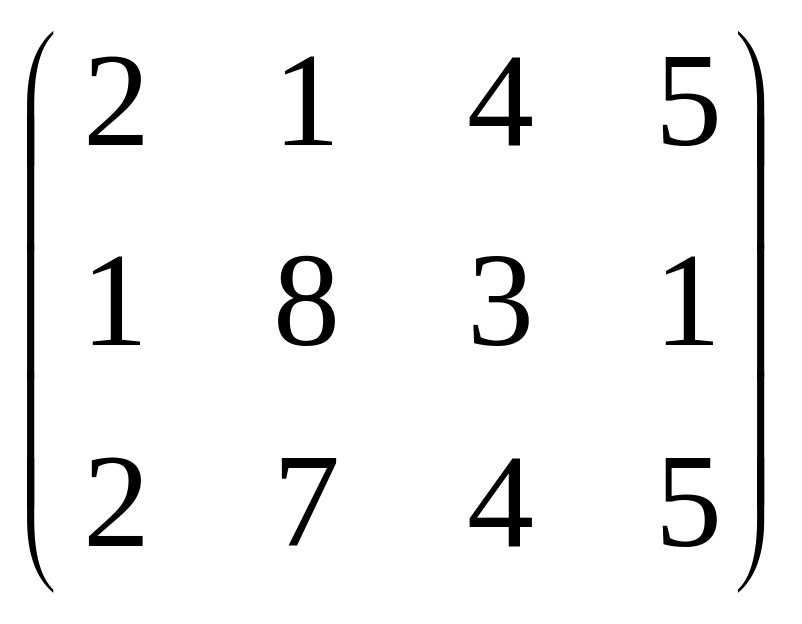
,
В=
,
С=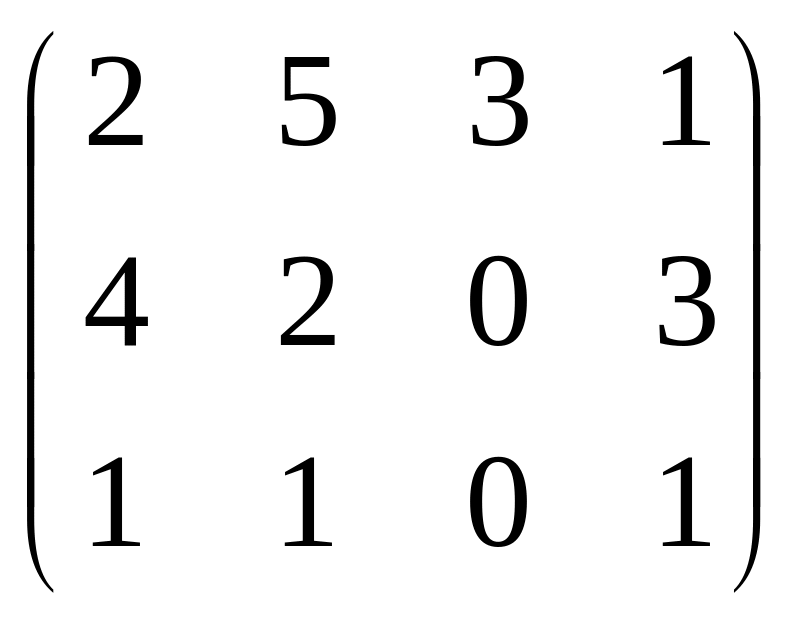
2. Найти значение матричного многочлена
2A2
+3A+7E
, если A
=
,
E==
3. Найти произведение матриц AB и BA, если
A
=
,
В =
,
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 5X1- X2+3 X3 X1 = 2X1+X3
X2 = X1 -2 X2 X2 = X2-5X3
X 3 = 7X2 - X3 X3 = 2X1
5. Вычислить определители
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
5 X1 + 11 X 2 +3X3 = 2
2X1 + 5X2 +X3 = 1
X1 -7 X2 -X3 =7
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
3 X1 +2X2+ 2Х3 +2 X4 =0 5X1+2X3=7
2Х1 +3 X2 +2X3 +5X4 =0 X1+2X2 +3X3=6
9 X1 +X2 +4X3 -5X4=0 X1-3X2 +X3=-1
Вариант 12
Найти матрицу 2A-7B+4C, если
A=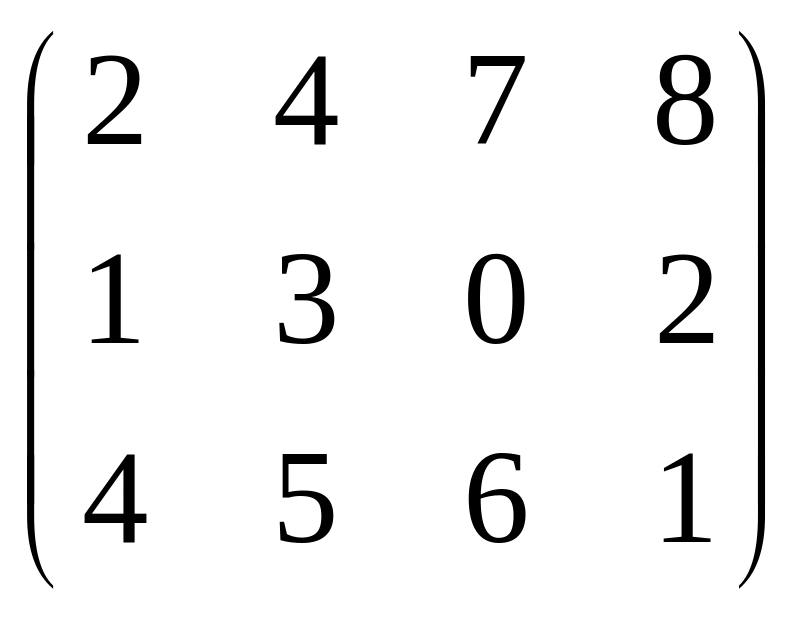
,
В=
,
С=
2. Найти значение матричного многочлена
3A2
+5A+3E
,если A
=
,
E=
=
3. Найти произведение матриц AB и BA, если
A
=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = X1-3X2+4 X3 X1 = 4 X1+5X2-3X3
X2 = 2 X1+X2 -5 X3 X2 = X1-X2-X3
X 3 = 3X1 +5X2+ X3 X3 = 7X1+ 4X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
X 1 + X 2 -6X3 = 6
3X1 - X2 -6X3 = 2
2 X1 + 3X2 +9X3 =6
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
7 X1 +X2+ 6X3 -X4 =0 7X1+2X2 -5X3=4
2X1 +2 X2 +3X3 +X4 =0 X1+X2 -3X3=-1
9 X1 +X2 +4X3 -5X4=0 X1+X2 +X3=3
Вариант 13
Найти матрицу 2A-8B+9C, если
A=
,
В=
,
С=
2. Найти значение матричного многочлена
5A2
+4A-3E
,если A
=
,
E=
=
3. Найти произведение матриц AB и BA, если
A
=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = X1-X2-X3 X1 = 9 X1+3X2+5X3
X2 = -X1+4 X2 +7 X 3 X2 = 2X1+3X3
X 3 = 8Х1 +X2-X3 X3 = X2-X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
8 X1 +6 X 2 +X3 = -7
10X1 +3X2 -3X3 = 3
6 X1 + 9X2 -2X3 =-4
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
9 X1 -3X2+5X3 +6X4 =0 2X1+3X2 -2X3=3
6X1 -2X2 +3X3 +X4 =0 X1+X2 -X3=0
9 X1 +X2 +4X3 -5X4=0 X1+X2 +3X3=5
Вариант 14
Найти матрицу 5A-2B+4C, если
A=
,
В=
,
С=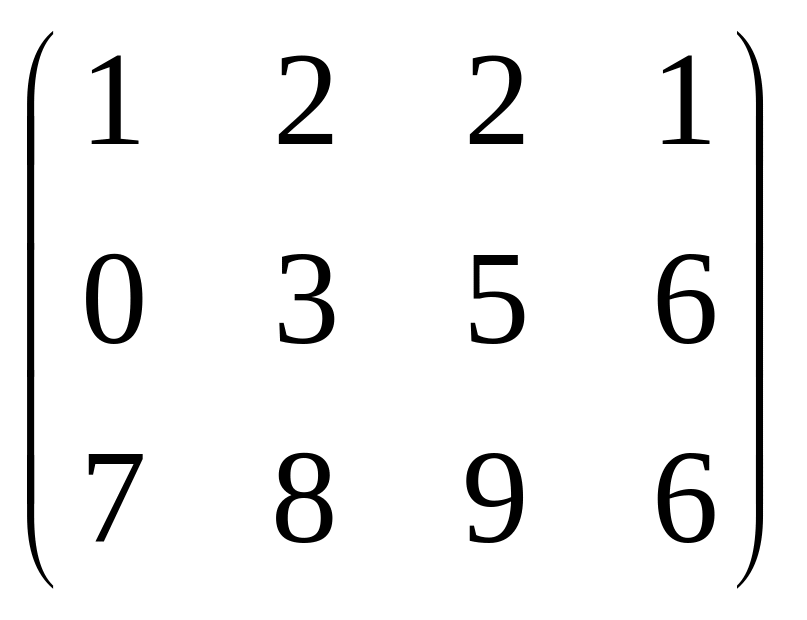
2. Найти значение матричного многочлена
2A2
+3A-4E
,если A
=
,
E=
=
3. Найти произведение матриц AB и BA, если
A
=
,
В=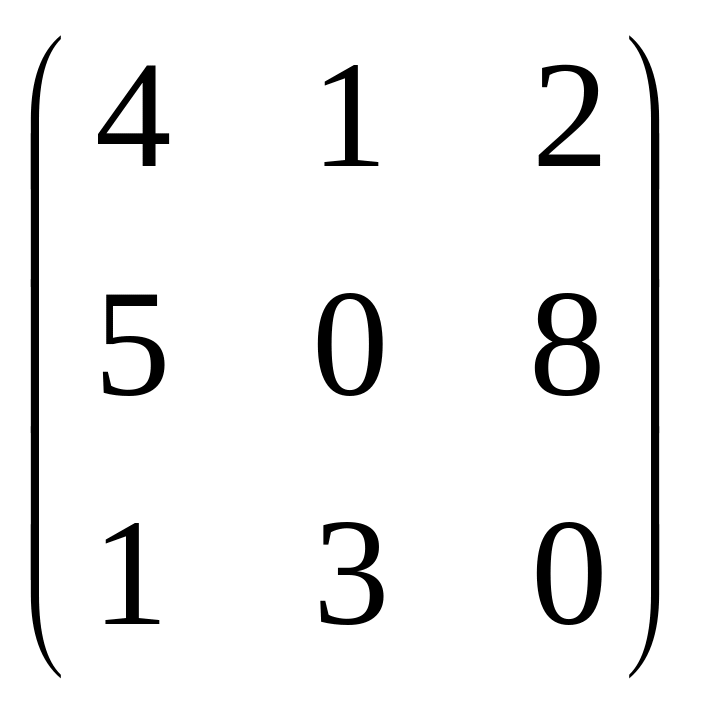
4 . Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = X1+2X2+2X3 X1 = 3X1+X2
X2 = -3X2+ X 3 X2 = X1-2 X2- X3
X 3 = 2X1 +3X2 X3 = 3X1+2X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 +4 X 2 +6X3 = 0
2X1 +2X2 +5X3 = 6
2X2 +3X3 =-6
7. Найти ранг матриц
А=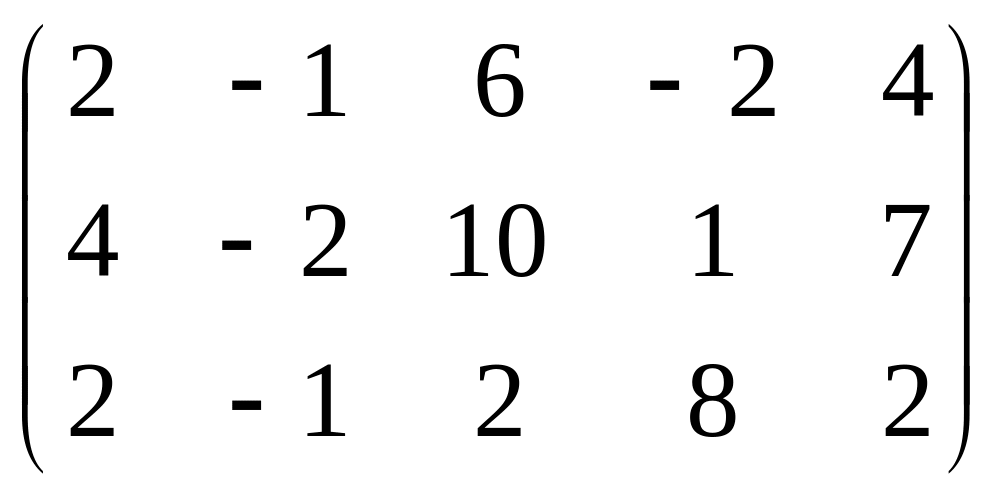
,
В=
8. Решить системы уравнений
2 X1 -X2+3X3 -7X4 =0 4X1+5X2 -3X3=6
6X1 -3X2 +X3 -4X4 =0 X1+X2 -3X3=-1
4 X1 -2X2 +14X3 -31X4=0 2X1-X2 -X3=0
Вариант 15
Найти матрицу 2A-7B+5C, если
A=
,
В=
,
С=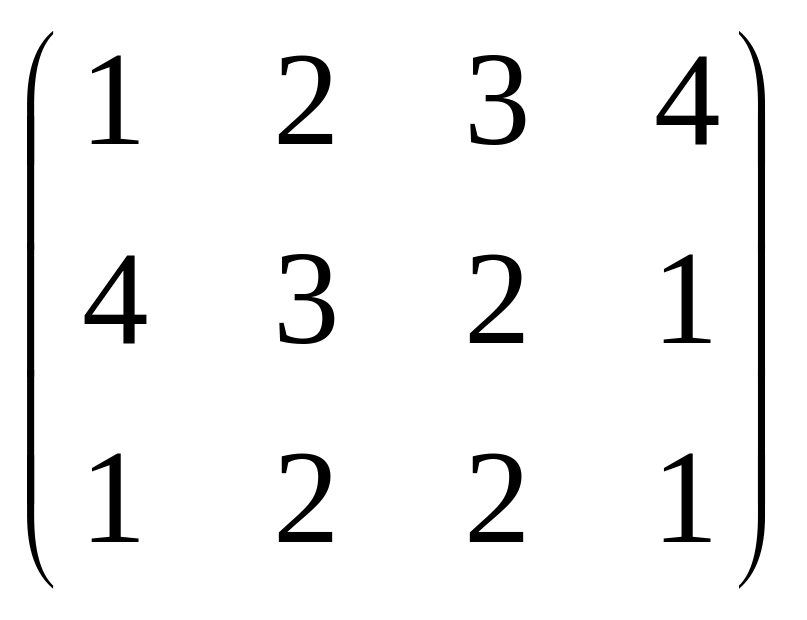
2. Найти значение матричного многочлена
5A2
+8A-9E
,если A=
,
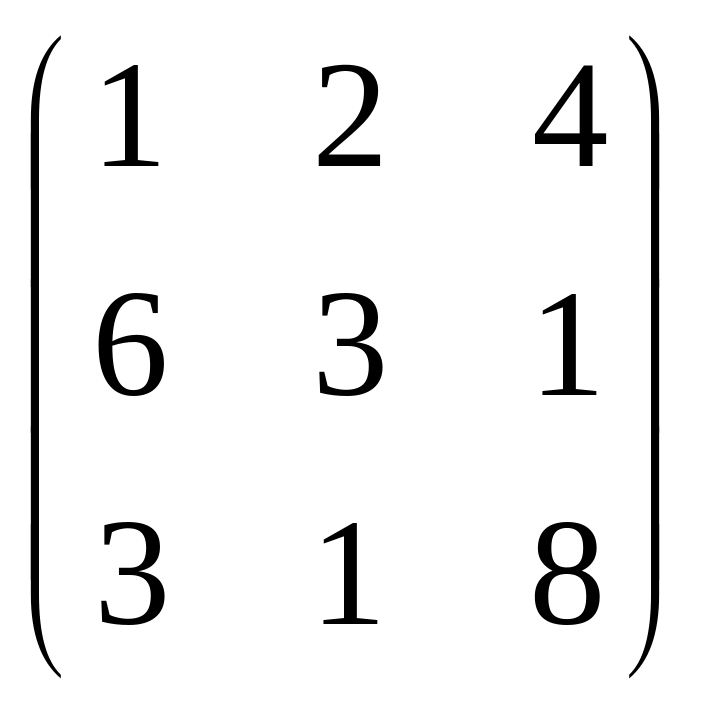E=
=
3. Найти произведение матриц AB и BA, если
A=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 4X1+3X2+5X3 X1 = -X1+5X2-3 X3
X2 = 6X1+ 7X 2+X3 X2 = X1- X2- X3
X 3 = 9X1 +X2+8X3 X3 = 7X1+4X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1 +2 X 2 -X3 = 4
4X1 +3X2 -X3 = 6
8X1 + 5X2 -3X3 =12
7. Найти ранг матриц
А=
,
В=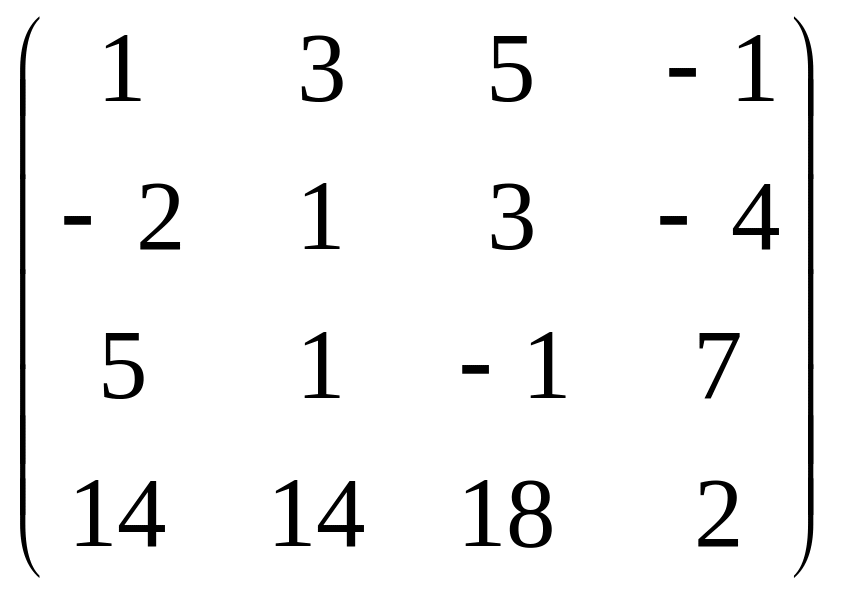
8 . Решить системы уравнений
3X1 -2X2+5X3 +4X4 =0 2X1-X2 +2X3=3
6X1 -4X2 +4X3 +3X4 =0 X1+X2 -X3=1
9 X1 -6X2 +3X3 +2X4=0 2X1+X2 +X3=4
Вариант 16
Найти матрицу 2A-7B+5C, если
A=
,
В=
,
С=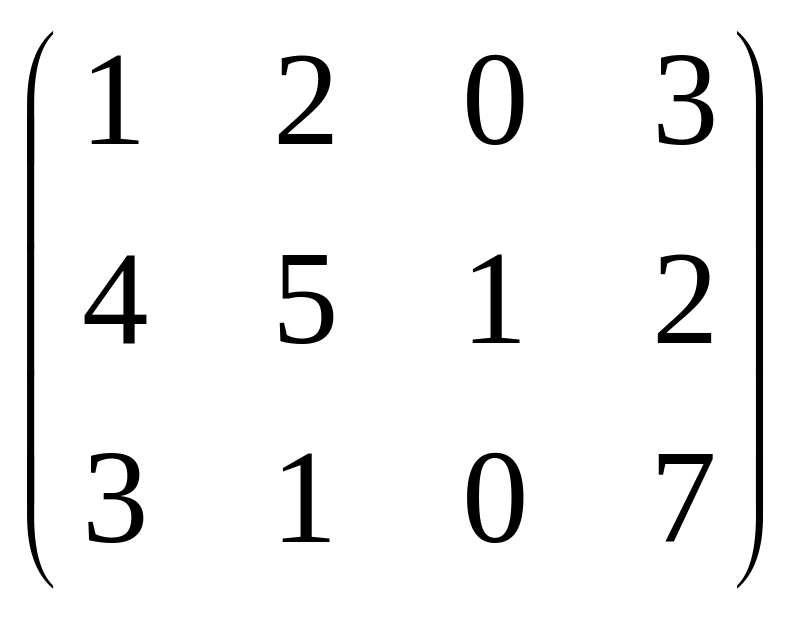
2. Найти значение матричного многочлена
5A2
+A+7E
,если А=
,
Е=
3. Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 7X1+3X2+4X3 X1 = X1+X2+6 X3
X2 = 4X1-9X 3 X2 = 3X1+7 X2
X 3 = 3X1 +X2+X3 X3 = X1+X3-X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
4 X1 -2 X 2 +3X3 = 6
2X1 +3X2 -4X3 = 20
3X1 -2X2 -5X3 =6
7. Найти ранг матриц
А=
,
В=
8 . Решить системы уравнений
X1 + X 2-3X3 +2X4 =0 4X1+3X2 -5X3=2
2X1 -3X2 +X3 -X4 =0 X1+X2 +4X3=6
4 X1 -X2 -5X3 +3X4=0 X1-X2 -X3=-1
Вариант 17
Найти матрицу 4A-7B+8C, если
А=
,
В=
,
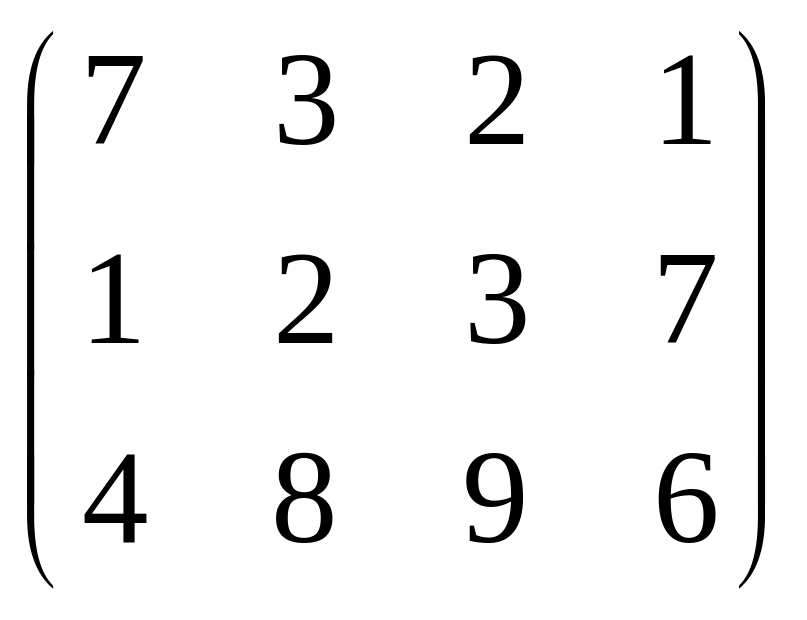С=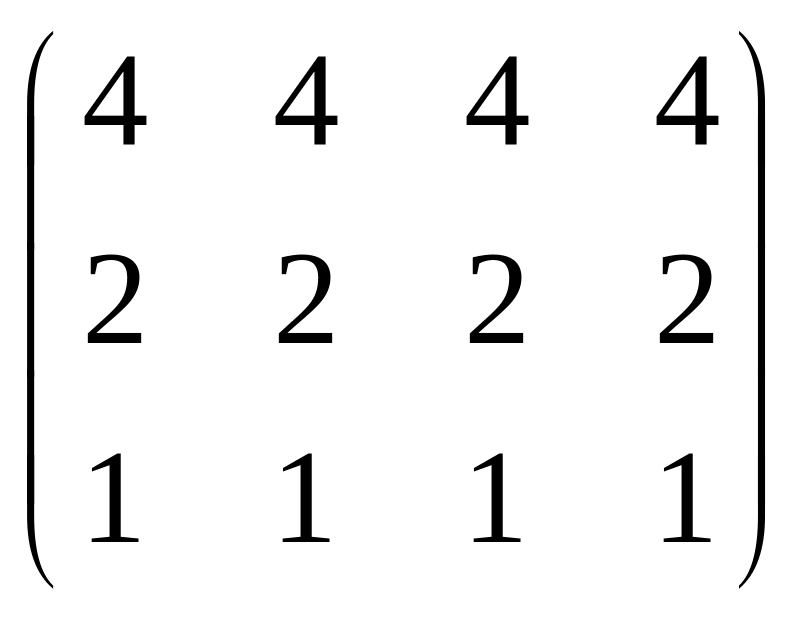
2. Найти значение матричного многочлена
7A2
+5A-8E
,если A=
,
E==
3. Найти произведение матриц AB и BA, если
A=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 7X1+4X3 X1 = X2-6X3
X2 = 4 X2-9X 3 X2 = 3X1+7 X3
X 3 = 3X1 +X2 X3 = X1+ X2-X3
Вычислить определители
;
;
;
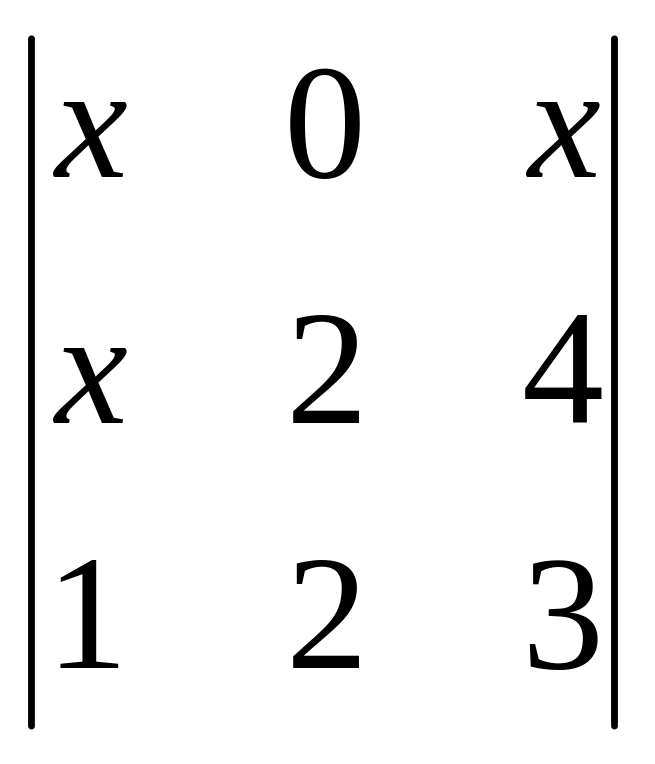6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
4 X1 -3X 2 +2X3 = 9
2X1 +5X2 -3X3 = 14
5X1 +6X2 -2X3 =18
Найти ранг матриц
А=
,
В=
8.Решить системы уравнений
7 X1 +5X2-3X3 +X4 =0 4X1-4X3 =0
3X1 +2X2 -3X3 +2X4 =0 X1+X2 +2X3=4
X 1+X2 +3X3 -3X4=0 2X1+X2 =3
Вариант 18
Найти матрицу 4A+B-6C, если
А=
,
В=
,
С=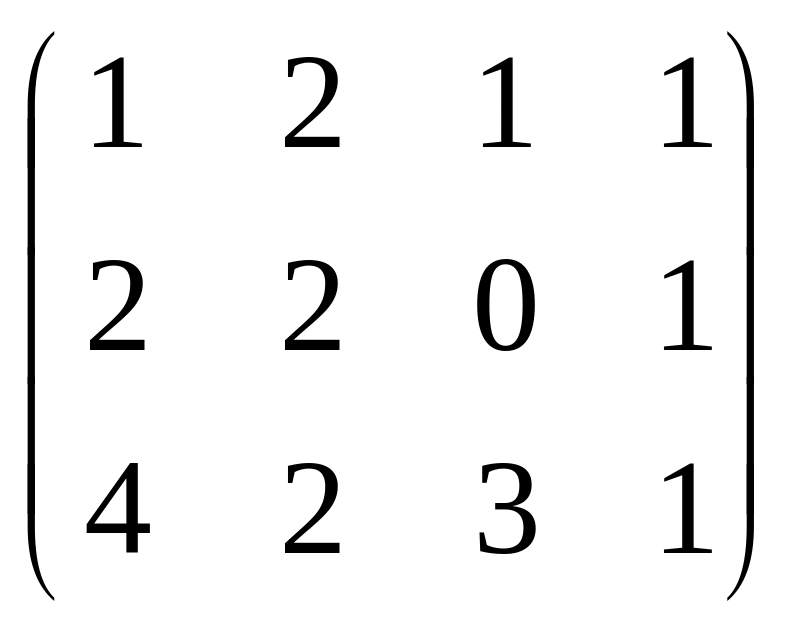
2. Найти значение матричного многочлена
3A2
+4A-7E
,если А=
,
Е=
3. Найти произведение матриц AB и BA, если
А=
,
В=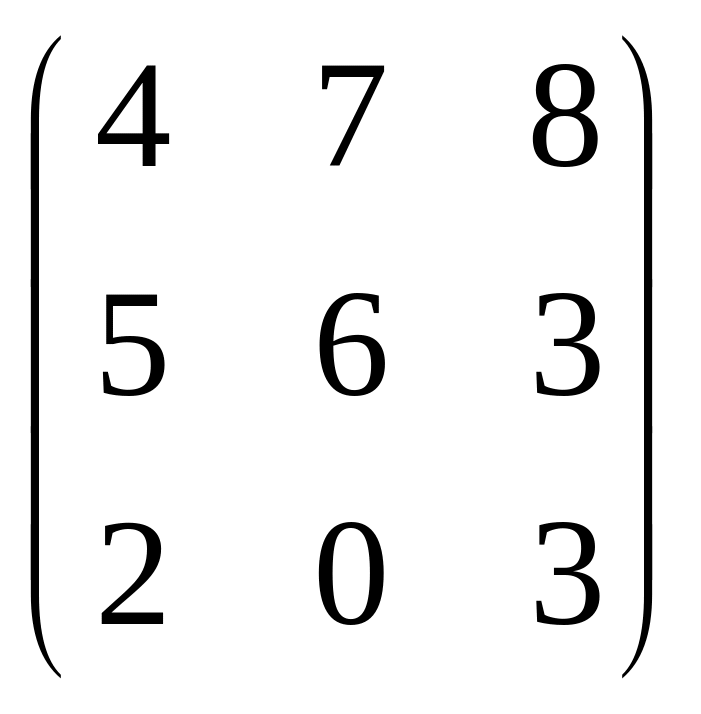
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 3X1+5X3 X1 = 2X1-X2-5X3
X2 = X1+X2+X 3 X2 = 7X1-X2+4 X3
X 3 = 3X1 -6X2 X3 = 6X1+4 X2-7 X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
X 1+X 2 -X3 = 1
6X1 +3X2 -6X3 = 2
-4X1 -X2 +3X3 =-3
7. Найти ранг матриц
А=
,
В=
Решить системы уравнений
5 X1 -3X2+4X3 +2X4 =0 X1+X2 -5X3 =-3
3X1 +2X2 -X3 +3X4 =0 X1+X2 +4X3=6
X 1+7X2 -6X3 +4X4=0 X1-X2+X3 =1
Вариант 19
Найти матрицу 4A+2B-6C, если
А=
,
В=
,
С=
2. Найти значение матричного многочлена
A2
+5A+6E
,если A
=
,
E==
3. Найти произведение матриц AB и BA, если
A
=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 3X1+5X3 X1 = 2X1-X2-5X3
X2 = X1+X2+X 3 X2 = 7X1+X2+4X3
X 3 = 3X1 -6X3 X3 = 6X1+4 X2-7X3
Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
7 X1-5X 2 = 31
4X1 +11X2 = 43
2X1 +3X2 +4X3 =20
7. Найти ранг матриц
А=
,
В=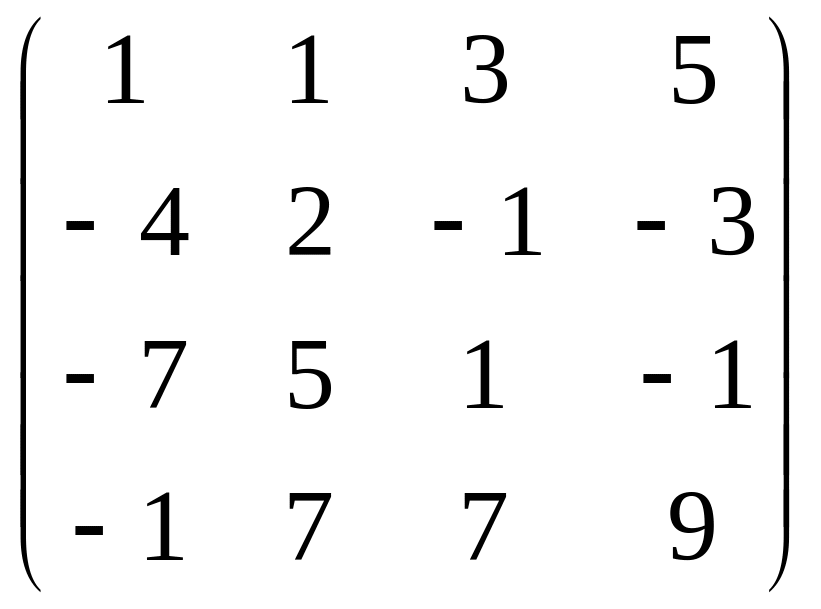
8. Решить системы уравнений
3 X1 +5X2-X3 +2X4 =0 X1-3X2 -2X3 =-4
2X1 +4X2 -X3 +3X4 =0 X1+X2 +3X3=6
X 1+3X2 - X3 +4X4=0 X1-X2+X3 =1
Вариант 20
Найти матрицу 4A+2B-3C, если
А=
,
В=
,
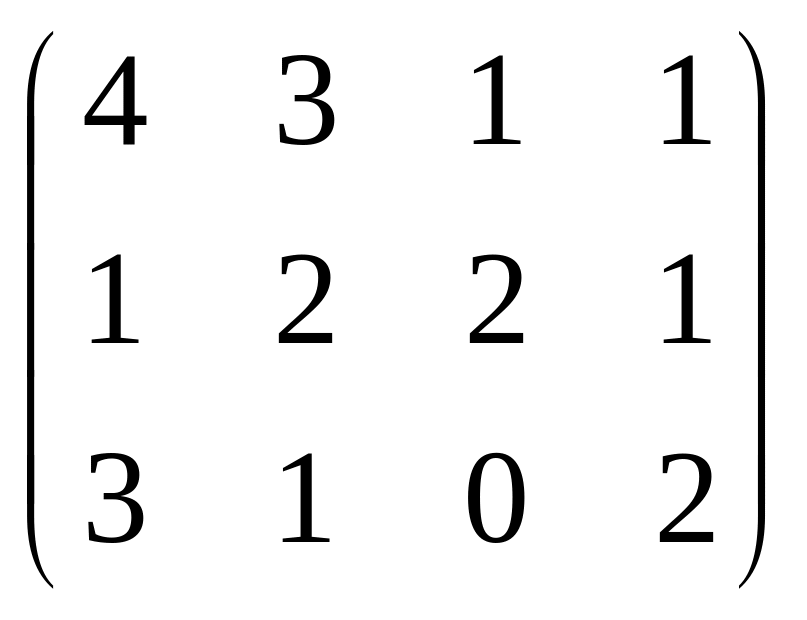С=
2. Найти значение матричного многочлена
2A2
+4A-3E
,если A=
,
E=
3. Найти произведение матриц AB и BA, если
A=
,
В=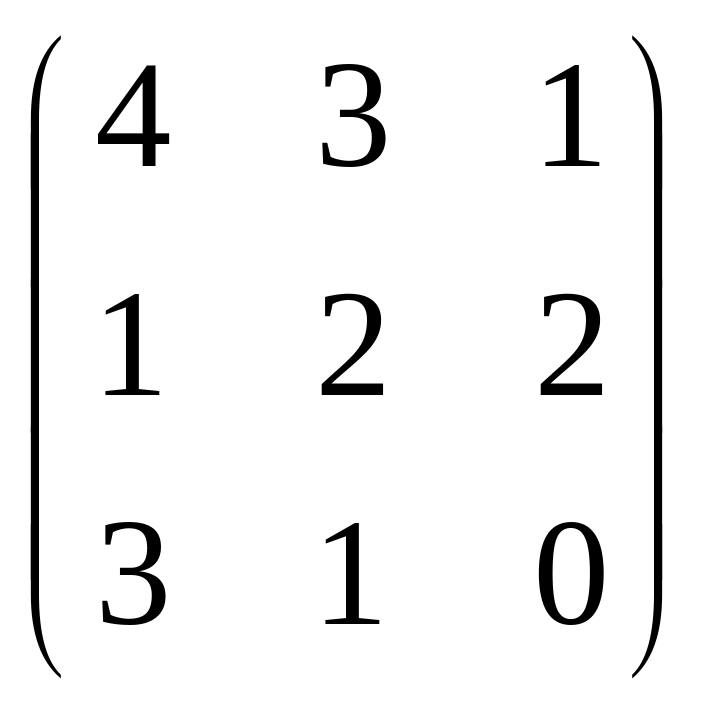
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 4X1+3X2+2X3 X1 = X1-2X2-X3
X2 = -2X1+X2-X 3 X2 = 3X1+X2+2 X3
X 3 = 3X1+X2 +X3 X3 = X1+2 X2+2X3
5. Вычислить определители
;
;
;
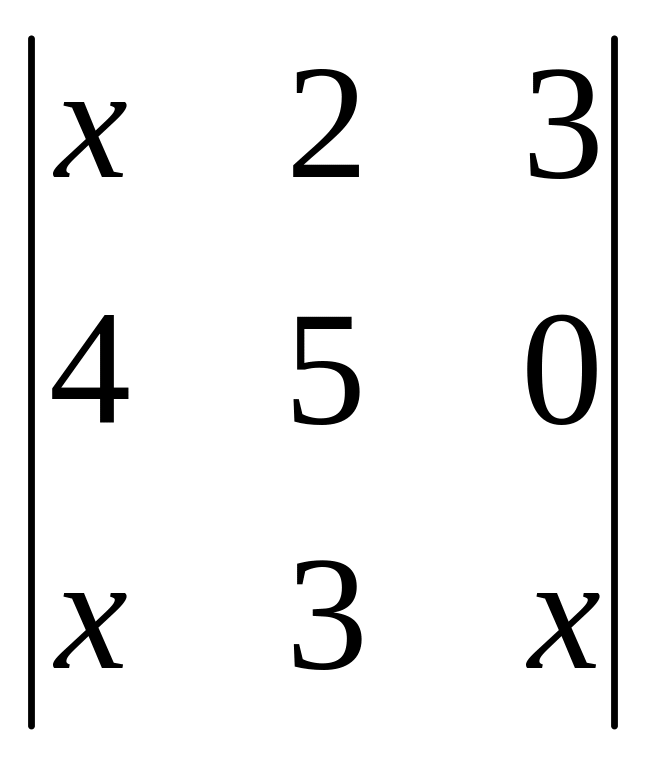6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
X 1+2X2 +X3 = 4
3X1 -5X2 +3X3 = 1
2X1 +7X2 -X3 =8
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
X1 +3X2-X3 -2X4 =0 3X1-3X2 +3X3 =3
2X1 +5X2 -8X3 -5X4 =0 X1-X2 +4X3=3
X 1+4X2 +5 X3 +X4=0 7X1-X2-3X3 =3
Вариант 21
Найти матрицу 4A-2B+7C, если
А=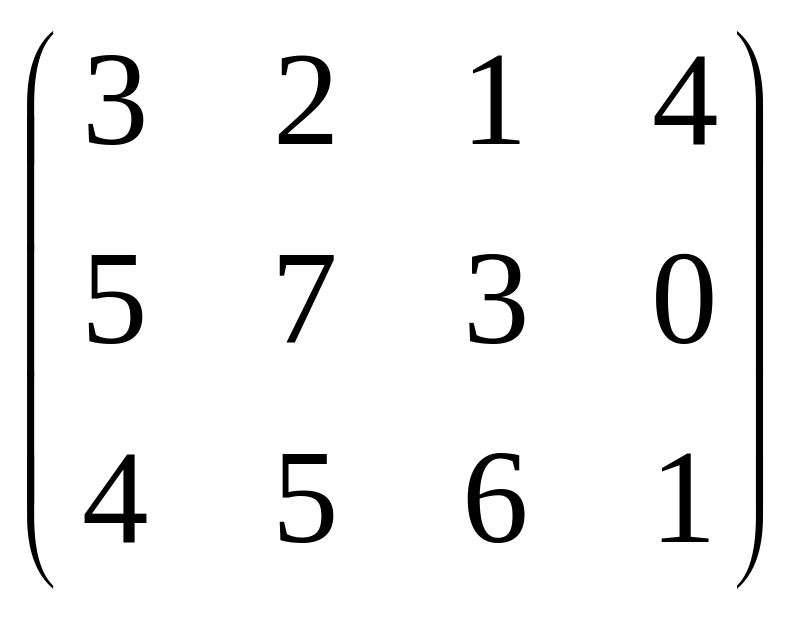
, В=
,
С=
2.
4A2
+3A-6E
,если А=
,
Е=
3. Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = -X1-X2-X3 X1 = 9X1+3X2+5X3
X2 = -X1+4X2+X 3 X2 = 2X1+3X3
X 3 = 8X1+X2 +X3 X3 = X2 -X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
X 1+X2 -Х3 = -2
4X1 -3X2 +X3 = 1
2X1 -X2 -X3 =1
Найти ранг матриц
А=
,
В=
Решить системы уравнений
7 X1 +5X2+3X3 +6X4 =0 3X1+2X2 +X3 =6
2X1 -X2 -X3 +4X4 =0 3X1-3X2 +3X3=3
X 1+8X2 +6 X3 -6X4=0 3X1-X2-2X3 =0
Вариант 22
Найти матрицу 4A+2B-6C, если
А=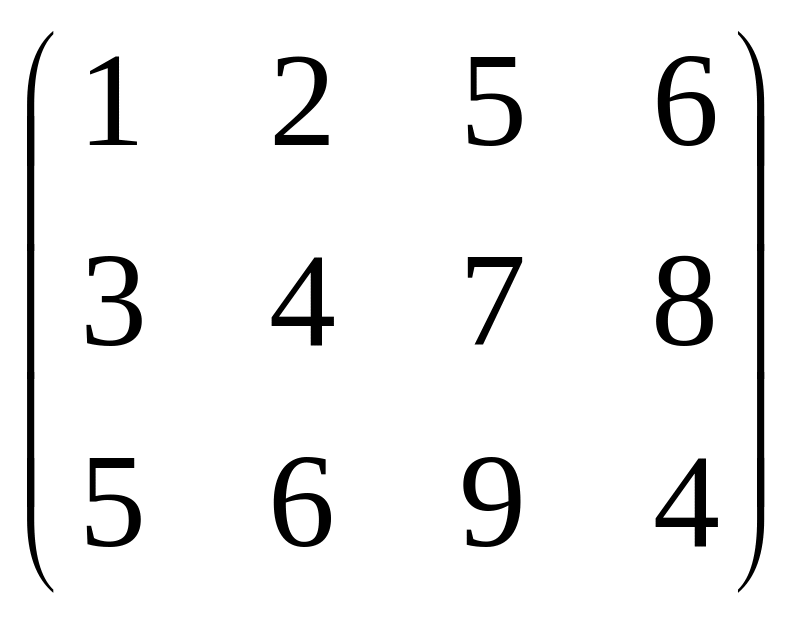
,
В=
,
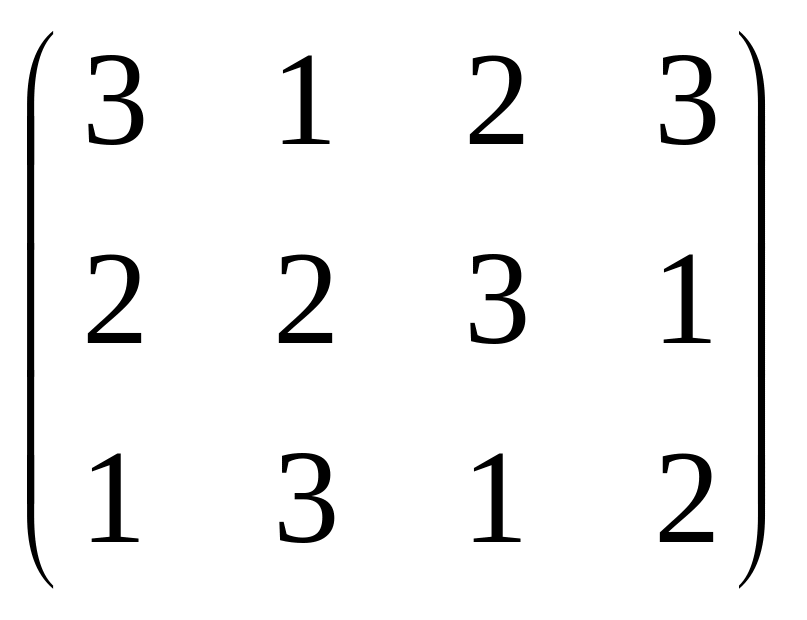С=
2. Найти значение матричного многочлена
3A2
+4A+7E
,если А=
,
E=
=
3. Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = 4X1+3X2+5X3 X1 = -X1+5X2-3X3
X2 = 6X1+7X2+X 3 X2 = X1-X2- X3
X 3 = 9X1+X2 +8X3 X3 = 7X1+4X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
2 X1-X2 +5X3 = 4
5X1 +2X2 +13X3 = 2
3X1 -X2 +5X3 =0
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
5 X1 -5X2+10X3 -X4 =0 4X1+X2-2X3 =3
3X1 +X2 +7X3 +X4 =0 X1-X2 +X3=4
X 1+7X2 +4 X3 +3X4=0 2X1+4X2-X3 =5
Вариант 23
Найти матрицу 4A-2B+3C, если
А=
,
В=
,
С=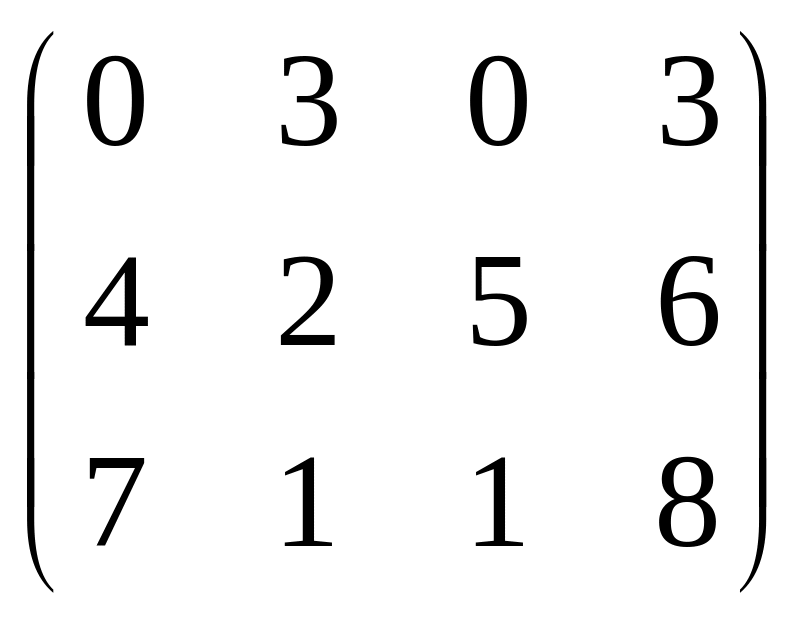
2. Найти значение матричного многочлена
3A2
+8А-9Е,если
А=
,
Е=
3. Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 , X2, X3 через X1, X2, X3 :
X1 = X1-3X2+4X3 X1 = 4X1+5X2-3X3
X2 = 2X1+X2-5X 3 X2 = X1-X2- X3
X 3 = -3X1+5X2 +X3 X3 = 7X1+4X3
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
3 X1+X2 +X3 = 5
X1 -4X2 -2X3 = -3
-3X1 +5X2 +6X3 =7
7.Найти ранг матриц
А=
,
В=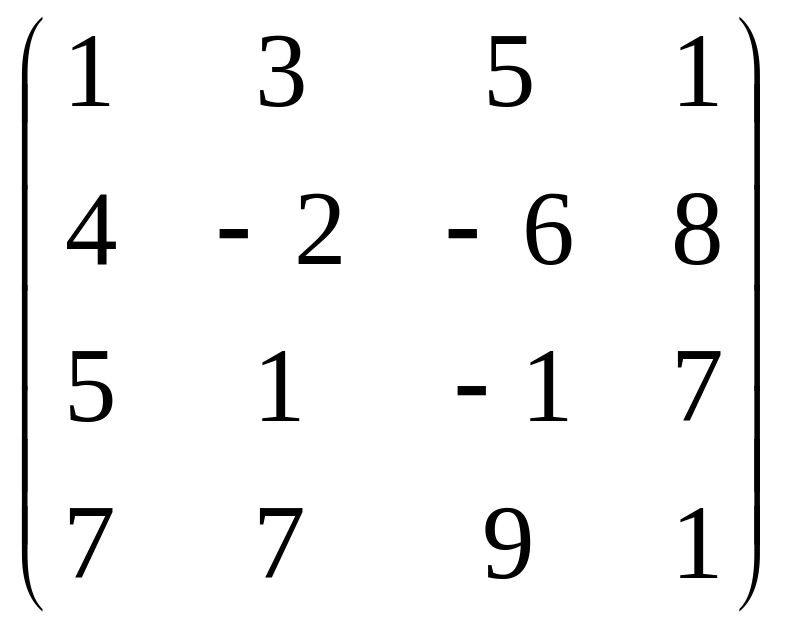
Решить системы уравнений
X 1 -3X2-4X3 +X4 =0 2X1+3X2+4X3 =9
5X1 -8X2 -2X3 +X4 =0 X1+X2 -X3=1
- 2X1-X2 -10 X3 -5X4=0 2X1-X2-X3 =0
Вариант 24
Найти матрицу 4A-2B+3C, если
А=
,
В=
,
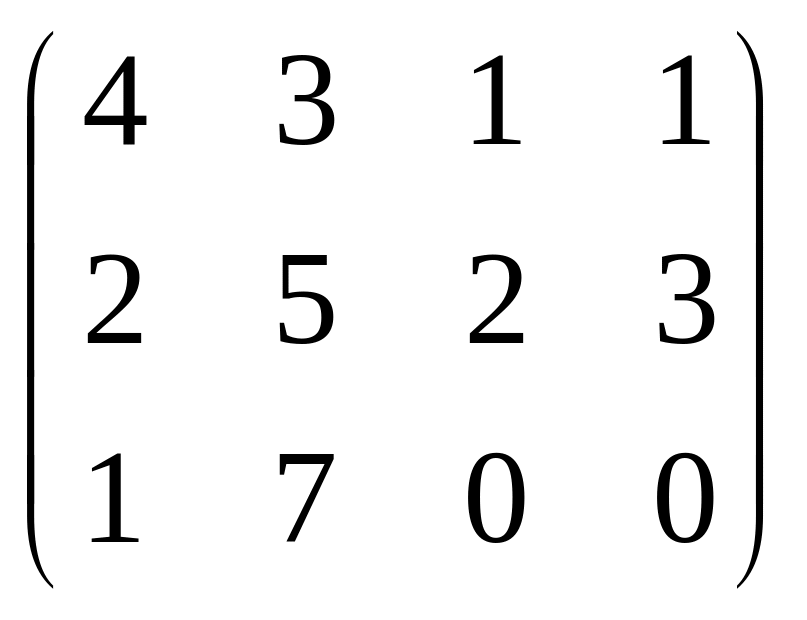С=
2. Найти значение матричного многочлена
3A2
+8A-E
, если А=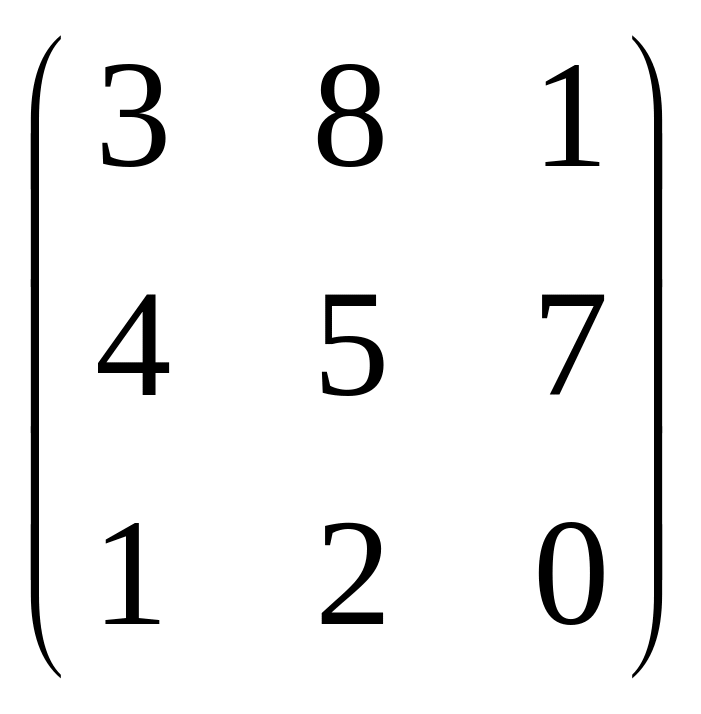
,
E=
3. Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 ², X2², X3 ² через X1, X2, X3 :
X1 ¢ = X1+2X2 +2X3 X1 ²= 3X1¢+X2¢
X2 ¢ = -3X2+X 3 X2 ²= X1¢- 2X2¢- X3¢
X 3 ¢ = 2X1 +3X3 X3 ²= 3X1¢+2X3¢
5. Вычислить определители
;
;
;
6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
5 X1+8X2 -Х3 = 7
2X1 -3X2 +2X3 = 9
X1 +2X2 +3X3 =1
7. Найти ранг матриц
А=
,
В=
Решить системы уравнений
3 X1 -2X2+X3 -4X4 =0 4X1+5X2 +X3 =10
2X1 -3X2 -2X3 +X4 =0 X1+X2 -X3=1
4 X1 -X2 +4 X3 -9X4=0 2X1-2X2+3X3 =3
Вариант 25
Найти матрицу 4A+5B-11C, если
А=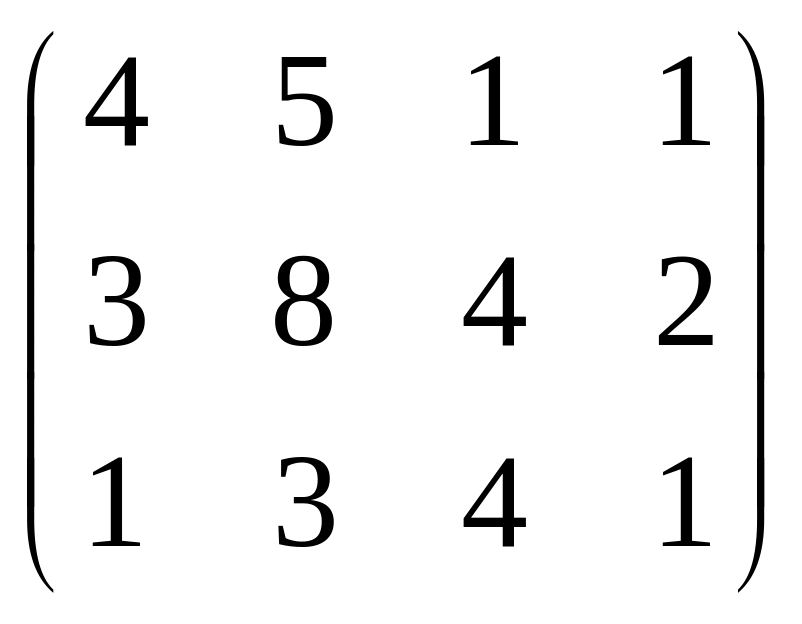
,
В=
,
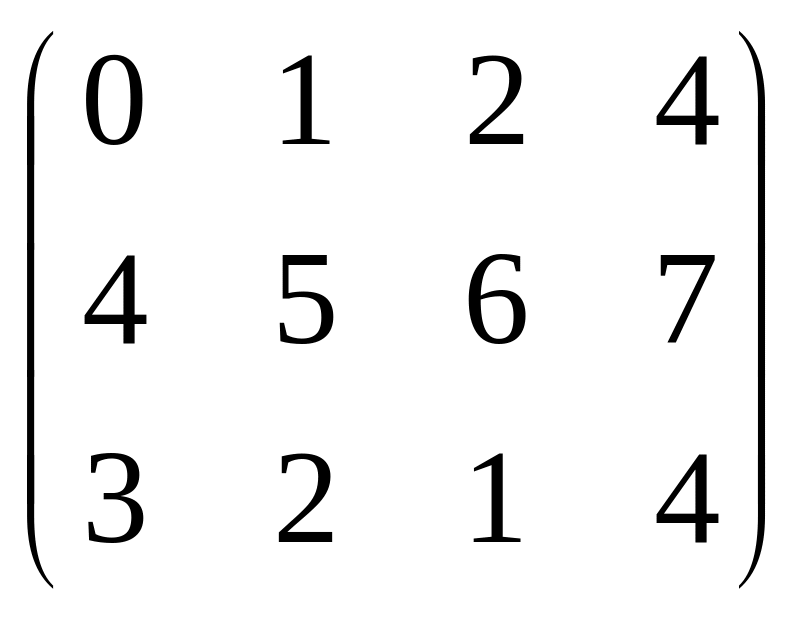С=
2. Найти значение матричного многочлена
4A2
+5A+E
, если А=
,
E==
3. Найти произведение матриц AB и BA, если
А=
,
В=
4. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X1 ², X2², X3 ² через X1, X2, X3 :
X1 ¢ = 5X1-X2+3X3 X1 ²= 2X1¢+X3¢
X2 ¢ = X1-2X2 X2 ²= X2¢-5X3¢
X 3 ¢ = 7X2 -X3 X3 ²=2X1¢
5. Вычислить определители
;
;
;
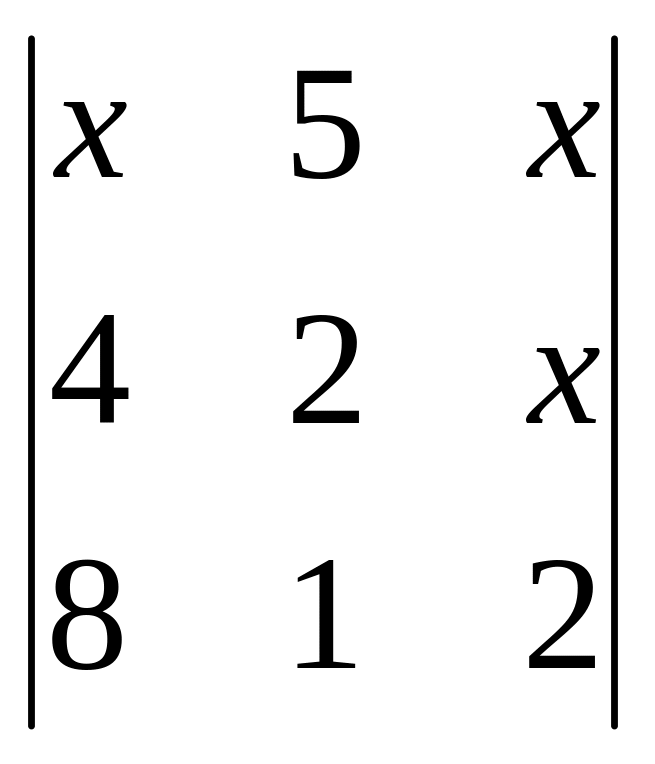6. Доказать совместность системы и решить ее двумя способами: методом Крамера и средствами матричного исчисления:
3 X1+4X2 +2Х3 = 8
2X1 -4X2 -3X3 =-1
X1 +5X2 +X3 =0
7. Найти ранг матриц
А=
,
В=
8. Решить системы уравнений
X 1 +4X2-3X3 +6X4 =0 -2X1+3X2 +X3 =2
2X1 +5X2 +X3 -2X4 =0 8X1-X2 +2X3=9
X 1+7X2 -10X3 +20X4=0 2X1+7X2 +7X3 =16
Модуль №2 Векторная алгебра
Вариант 1
1.
Векторы
и
даны
геометрически. Построить каждый из
следующих векторов: 1)
;
2)
;
3)
;
4)
;
2.На
плоскости даны точки А(-2, 3); В(3, 3); С(2,
-2). В начале координат приложены силы
.
Построить равнодействующую
.
Выразить силы
через
единичные векторы
и
координатных осей. Найти величину
равнодействующей
.
3.
Разложить геометрически и аналитически
вектор
по векторам
и
,
если
=5
+2
;
=-
-3
;
=-2
+3
.
4.Под
действием силы
={2,
-3, -1} материальная точка переместилась
из точки A(2,
-2,
1)
в
точку B(7,
-3,
1).
Вычислить
работу силы
.
5.Даны
векторы
={0,
-3, 6};
={3,
-6, 2}. Найти: 1) (
,
);
2)
;
3) (
+
-
);
4)
(
+
);
5)
-
орт
.
6. Даны
векторы
=
2
-3
;
=
+2
,
где
=
=2;
(
)=
Найти:
1) (
,
);
2)
;
3) (
+
-
);
4)
(
+
);
7. Найти площадь треугольника с вершинами A(4, 2, -1); B(3, 0, 4); C(0, 0, 4).
8. Найти площадь параллелограмма, построенного на векторах = 2 -3 ; = +2 , где = =2; ( )= .
9. Даны
три силы, приложенные к точке A(2,
1, 2)
=
-2
+
;
=
+
+
;
=-2
-3
+
.
Найти момент их равнодействующей
относительно т. B(0,
-1, -1).
10. Установить, компланарны ли векторы =4 -2 +4 ; =3 -4 +7 ; = +2 -3 ;
11.Даны
координаты
вершин
пирамиды
A
A
A
A
:
A
(2,
4, -6);
A
(1,
3, 5); A
(0,
-3, 7); A
(3,
2, 3). Требуется
средствами векторной алгебры найти:
угол между ребрами A A и A A ;
площадь грани A A A ;
проекцию вектора
на
объем пирамиды.
Вариант 2
1.Векторы
и
даны
геометрически. Построить каждый из
следующих векторов: 1)
;2)
;3)
;
4)
;
2. На плоскости даны точки А(-1, 5); В(3, 5); С(4, -1). В начале координат приложены силы . Построить равнодействующую . Выразить силы через единичные векторы и координатных осей. Найти величину равнодействующей .
3. Разложить геометрически и аналитически вектор по векторам и , если =3 ; =- +3 ; =-2 -2 .
4.Под действием силы ={2, -3, -1} материальная точка переместилась из точки A(-1, 2, 3) в точку B(3, 1, 2). Вычислить работу силы .
5.Даны векторы ={2, -2, 2}; ={3, 0, -4}. Найти: 1) ( , ); 2) ;
3) ( + - ); 4) ( + ); 5) - орт .
6. Даны
векторы
=
3
+2
;
=
2
-
,
где
=3;
=2;
(
)=
Найти: 1) (
,
);
2)
;
3) (
+
-
);
4)
(
+
);
7. Найти площадь треугольника с вершинами A(1, 1, 2); B(2, 3, -1); C(2, -2, 4).
8. Найти площадь параллелограмма, построенного на векторах
= 3 +2 ; = 2 - , где =3; =2; ( )=
9. Сила =3 -2 + приложена к точке A(3, 2, -1). Найти величину и направление момента этой силы относительно т. B(3, 1, -1).
10. Установить, компланарны ли векторы = - +2 ; =3 +5 ; =5 +3 +4 ;
11. Даны координаты вершин пирамиды A A A A A (-2, 3, 5);
A (1, -3, 4); A (7, 8, -1); A (-1, 2, -1).Требуется средствами векторной алгебры найти:
угол между ребрами A A и A A ;
площадь грани A A A ;
проекцию вектора на
объем пирамиды.