3 Указания к разработке комплексных чертежей позиционных и метрических задач

(Указания выполнены в виде учебного примера для варианта 0)

Задача № 1. Построить следы плоскости, заданной прямой АВ и точкой О (началом координат), и определить точку пересечения прямой ЕД с заданной плоскостью. Данные для своего варианта взять из таблицы №1. Пример выполнения задачи №1 приведен на рисунке 4.

Последовательность оформления и решения задачи.

На чертежном листе формата A3 выполнить чертежную рамку по ГОСТ 2.301—68. В удобном месте чертежного ноля нанести оси координат и из таблицы 1, согласно своему варианту, взять координаты точек А,В,Е и D. Масштаб принять, исходя из условия, что комплексный чертёж будет занимать не менее ¾ части чертежного листа.

Решение:

Искомые следы плоскости обозначить черезf_2Σ° и h_1Σ°,

где f_2Σ° - фронтальный след плоскости Σ (АВ,О); h_1Σ° -горизонтальный след плоскости Σ(АВ,О).

Для того, чтобы провести фронтальный след (f_2Σ°) плоскости Σ необходимо иметь две точки этой плоскости, лежащие на фронтальной плоскости проекций П₂. Одна такая точка О уже дана и является точкой

схода следов ΣX. Второй точкой будет служить фронтальный след

N(N₂;N₁) прямой AB(A₁B₁ А₂В₂). Для нахождения фронтального следа прямой выполнить следующие действия:

- продолжить горизонтальную проекцию прямой АВ до пересечения с осью ОХ в точке N₁. В этой точке восстановить

22

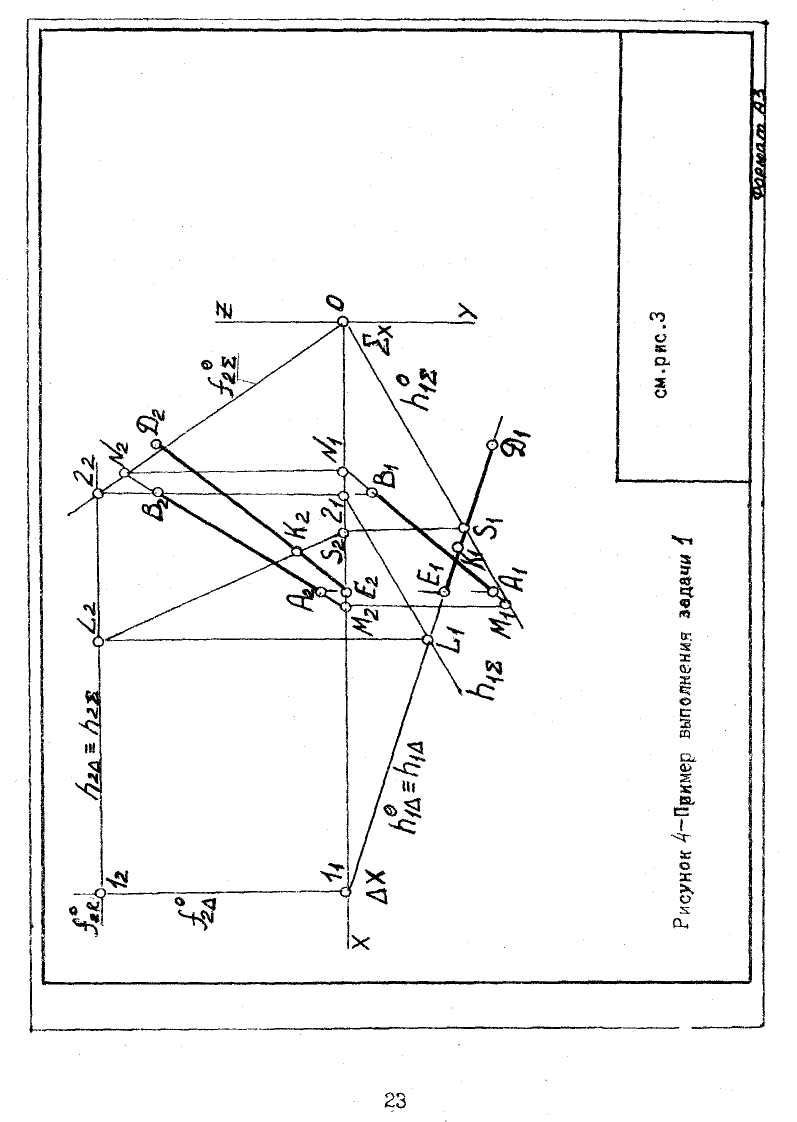
перпендикуляр к оси проекций до пересечения с фронтальной проекцией прямой в точке N₂(N). Эта точка является фронтальным следом прямой;

-через точки N(N₂) и ΣX следует провести фронтальный след (f⁰_2Σ)

плоскости Σ .

Для построения горизонтального следа (h⁰_1Σ) плоскости Σ, необходимо найти горизонтальный след М (М₁ ; М₂) прямой

АВ(А₁В₁, А₂В₂). Нахождение горизонтального следа прямой необходимо выполнить в следующей последовательности:

- продолжить фронтальную проекцию прямой до пересечения с осью ОХ в точке М₂;

- в точке М₂ восстановить перпендикуляр к оси проекций до пересечения с горизонтальной проекцией прямой в точке М(М₁). Эта точка является горизонтальным следом прямой;

-через точки М (М₁ ;М₂) и ΣX провести горизонтальный след (h⁰_1Σ) плоскости Σ. Нахождение точки пересечения прямой ЕD(Е₁D_1, Е₂D₂) с плоскостью Σ (АВ,О) следует выполнить в такой последовательности, для чего заключить прямую DЕ, например, в горизонтально-проецирующую плоскость ∆ _┴ П₁.

Плоскости Σ и ∆ пересекаются по прямой общего положения, проходящей через точку-след S (S₁,S₂) пересечения горизонтальных следов плоскостей. Из рисунка 4 видно, что фронтальные следы плоскостей в пределах чертежа не пересекаются. Поэтому следует найти другую произвольную точку прямой пересечения, общую для этих плоскостей. Для нахождения такой точки необходимо ввести вспомогательную плоскость R, например, параллельную плоскости П₁, которая, как известно, пересекает каждую из данных плоскостей по горизонталям. На их пересечении получится вспомогательная точка L(L₁,L₂) общая для данных плоскостей.

Затем, соединив найденные точки L и S, найти точку К(К_1,К₂) пересечения прямой LS со стороной DE.

На чертеже следы плоскостей показать тонкой линией красного цвета. Решение задачи может быть и другим.

24

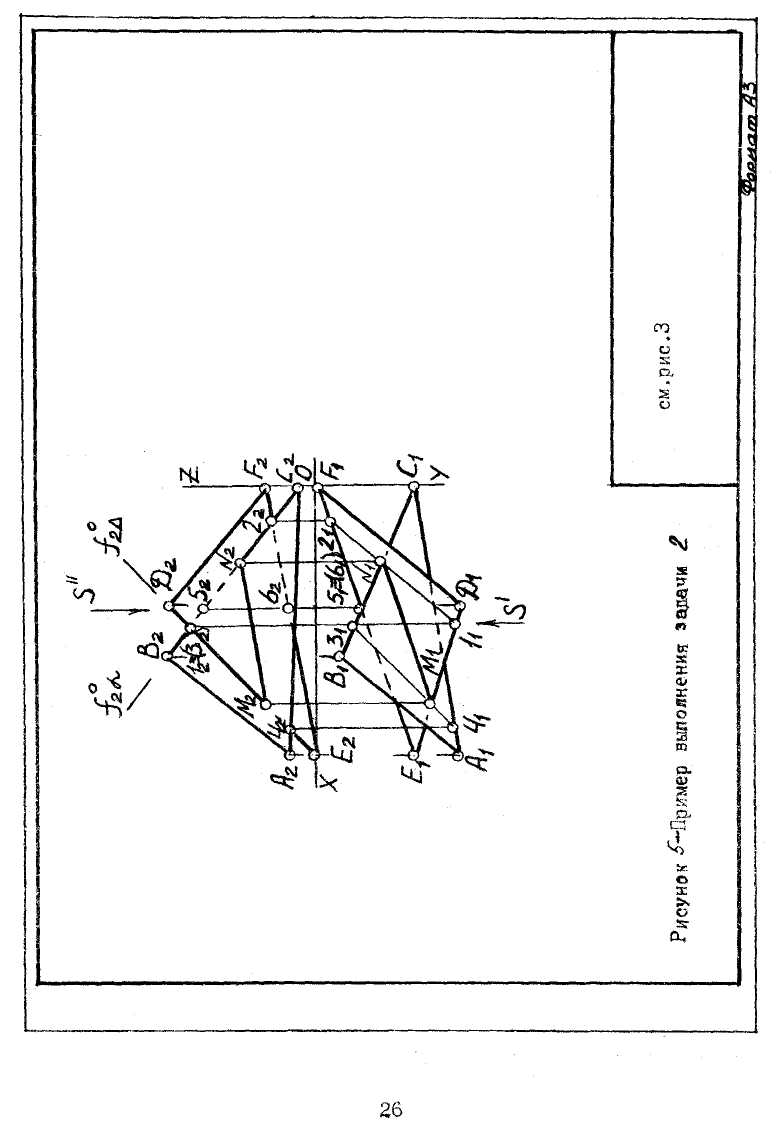
Задача № 2. Построить линию пересечения треугольников АВС и DEF и показать видимость их в проекциях. Данные для своего варианта взять из таблицы 1. Пример выполнения задачи 2 приведен на рисунке 5.

Последовательность решения и оформления задачи.

На чертежном листе формата А3 выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. В середине чертежного поля нанести оси координат и из таблицы 1, согласно своему варианту, взять координаты точек А,В,С,D,Е и F. Масштаб принять, исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа.

Решение:

Через сторону ВС треугольника АВС проводится фронтально-проецирующая плоскость α _┴ П₁. Определяется линия 1-2(1₂2₂;1₁2₁) пересечения плоскости α с плоскостью DEF. Затем находится точка N(N₂N₁) пересечения прямой ВС с линией 1-2. Через сторону DЕ треугольника DEF проводится фронтально-проецирующая плоскость

∆ _┴ П₂. Строится линия 3-4(3₂4₂,3₁4₁)) пересечения плоскости ∆ с плоскостью АВС. Находится точка М(М₁,М₂) пересечения прямой DЕ с линией 3-4. Соединяются найденные точки М и N. Прямая МN - линия пересечения двух треугольников. Видимость на эпюре выполняется на основании выявления и анализа конкурирующих точек на скрещивающихся прямых. Для этого из кажущейся точки пересечения прямых ВС и DЕ на плоскости П₂, являющейся фронтальной проекцией двух конкурирующих точек 1 и 3, лежащих на этих прямых, проводится проецирующий луч S' и анализируется положение прямых по горизонтальным их проекциям, т.е. Y₁ >Y₃. Из этого следует, что отрезок М₂D₂ видим, а участок М₂3₂ - невидим. Аналогично анализируется взаимное положение ВС и ЕF на плоскости П₁. Исходя из этого, устанавливается, что В₁N₁ видимая на горизонтальной проекции П₁, т.е Z₅ > Z_6.

Проекции N₁M₁ и N₂М₂ показать сплошными линиями красного цвета.

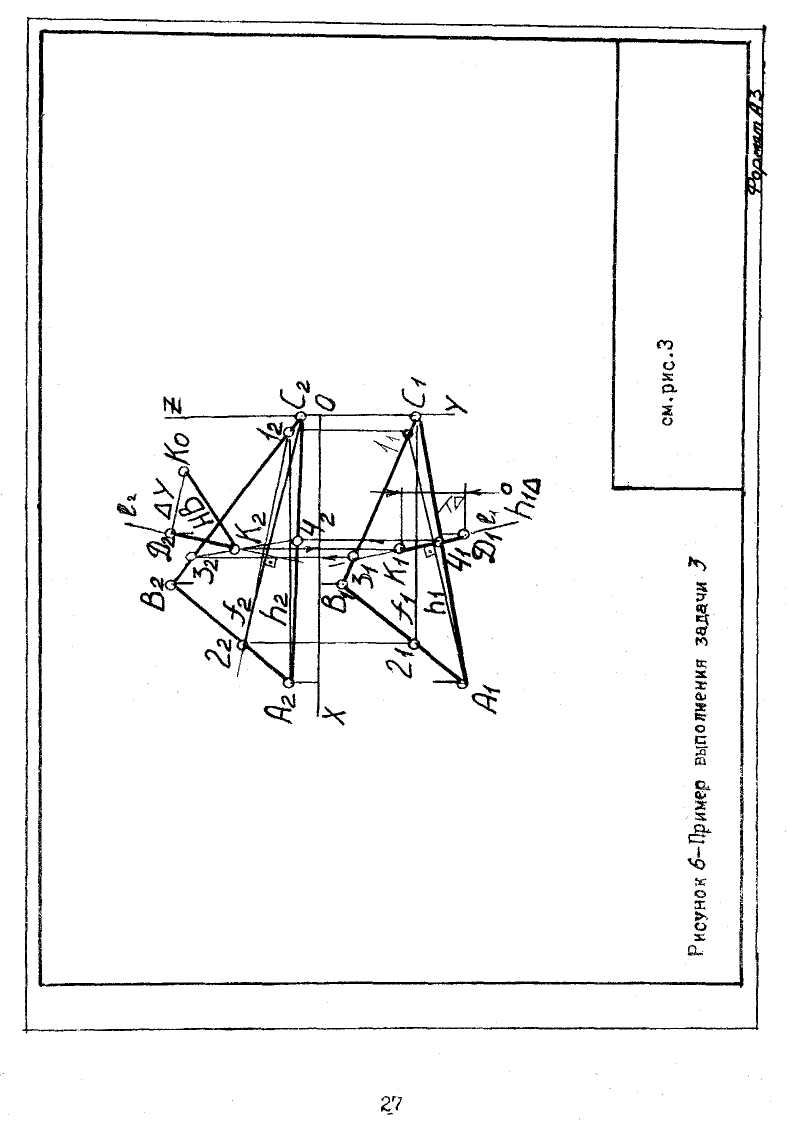
Задача № 3. Определить кратчайшее расстояние от точки D до плоскости треугольника АВС. Данные из своего варианта взять из таблицы 1. Пример выполнения задачи 3 приведен на рисунке 6.

25

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. В середине чертежного поля нанести оси координат и из таблицы 1, согласно своему варианту, взять координаты точек А,В,С и D. Масштаб принять, исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа.

Решение:

В плоскости треугольника АВС проводится горизонталь h(h₂,h₁) и фронталь f(f₁,f₂) Из точки D следует опустить перпендикуляр на соответствующие проекции фронтали f и горизонтали h, т.е. из D₂ опускается перпендикуляр на f₂, а из D₁ на h₁. Через перпендикуляр и точку D следует провести вспомогательную плоскость ∆ _┴ П₁.

Определяется линия 3-4(3₂4₂,3₁4₁) пересечения плоскости ∆ с плоскостью треугольника АВС. Находится точка К(К₂,К1) пересечения прямой 3-4(3₂4₂,3₁4₁) с перпендикуляром L. Для определения натуральной величины отрезка следует построить прямоугольный треугольник К₂D₂Ко. В треугольнике К₂D₂K₀ катет D₂Ко равен разности расстояний точек D и К до фронтальной плоскости проекций (П₂). Линия D₂К₀ является натуральной величиной кратчайшего расстояния от точки D до плоскости треугольника АВС. Линии D₂Ко,К₂D₂,К₁D₁ показать основными сплошными линиями толщиной 0,8... 1,0 мм. красным цветом.

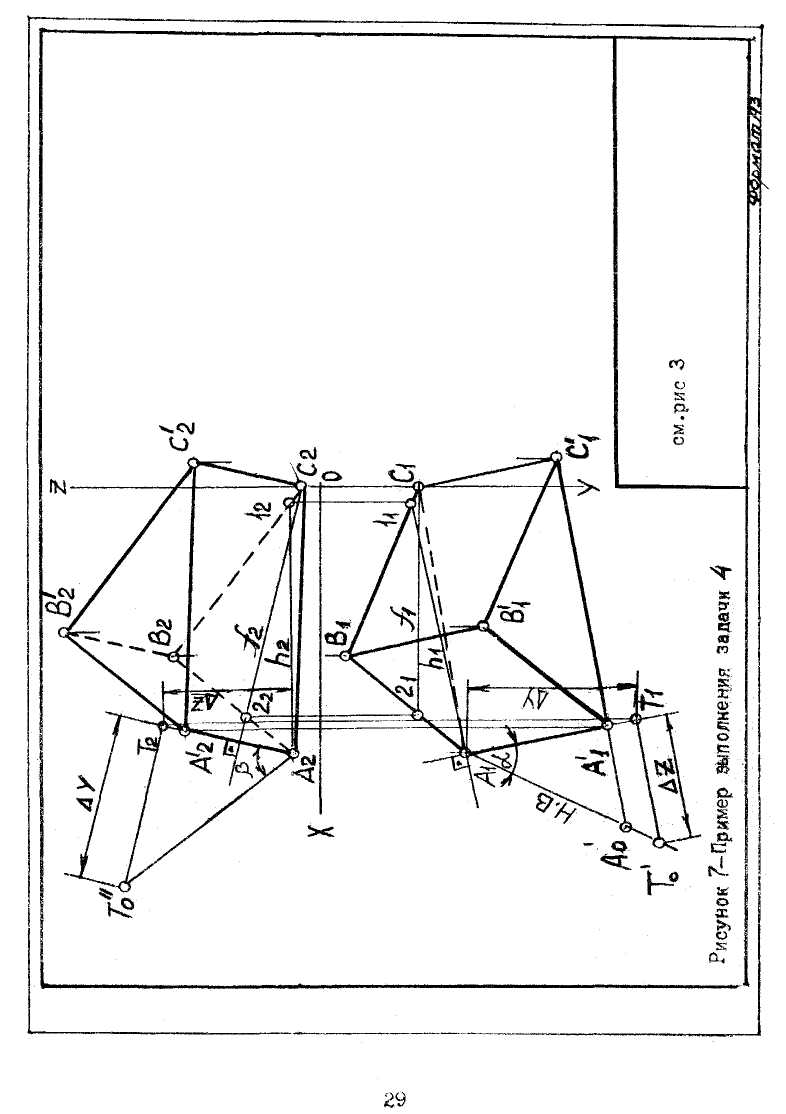
Задача № 4. Построить проекции прямой призмы, основанием которой является треугольник АВС, а ребро а'а определяет высоту призмы, и найти углы αиβ наклона ребра призмы к горизонтальной и фронтальной плоскостям проекций. Данные для своего варианта взять из таблицы 2. Пример выполнения задачи 4 приведен на рисунке 7.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. В середине чертежного поля нанести оси координат .из таблицы 2, согласно своему варианту, взять

28

координаты точек А,В и D. Масштаб принять, исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа.

Решение:

Проводим в заданной плоскости, например, через точку А, горизонталь h(h₁,h₂), а фронталь f(f₁,f₂) - через точку С. Строится проекция искомого ребра перпендикулярно фронтальной проекции фронтали (T₂А_{2 ┴} f₂), и горизонтальная проекция -перпендикулярно к горизонтальной проекции горизонтали (Т₁А_{1 ┴} h₁). Для определения натуральной величины отрезка АТ и углов α и β на рисунке 7 следует построить прямоугольные треугольники А₁T₁T'₀ и A₂T₂T''_0. В треугольнике А₁T₁T'₀ катет T₁T'₀ равен разности расстояний точек А и Т до горизонтальной плоскости проекций |∆Z = Z_T-Z_A| угол между катетами горизонтальной проекции (A₁T₁) и гипотенузой равен углу (α) наклона прямой к горизонтальной плоскости проекции (П₁). В треугольнике A₂T₂T''₀ катет T₂T''₀ равен разности расстояний точек А и Т до фронтальной плоскости црекций |∆Y = Y_T -Y_A|; угол между катетами фронтальной проекции (А₂Т₂) и гипотенузой равен углу (β) наклона прямой к фронтальной плоскости проекций (П₂). Откладывается на гипотенузе построенного треугольника, например А₁T₁T'₀, отрезок AA'₀ длиной 70 мм, и опускается из точки A'₀ перпендикуляр на прямую A₁T₁ до пересечения с ней в точкеA₁'. По точке A₁' определяется точка A₂' на прямой А₂Т₂. Проекциями искомого отрезка высоты призмы являются А₁А₁' , А₂А₂'. Проводятся параллельно прямые АА'║ВВ' ||СС' и соединяются их вершины. Видимость сторон призмы

на плоскостях проекций определяется с помощью конкурирующих точек.

Все видимые проекции линий призмы показать основными сплошными линиями толщиной 1... 1,4 мм черным цветом, а невидимые — штриховой.

Задача № 5. Определить кратчайшее расстояние между скрещивающимися прямыми СВ и DF и построить проекции общего к ним перпендикуляра. Данные для своего варианта взять из таблицы 1. Пример выполнения задачи 5 приведен на рисунке 8.

Последовательность решения и оформления задачи.

30

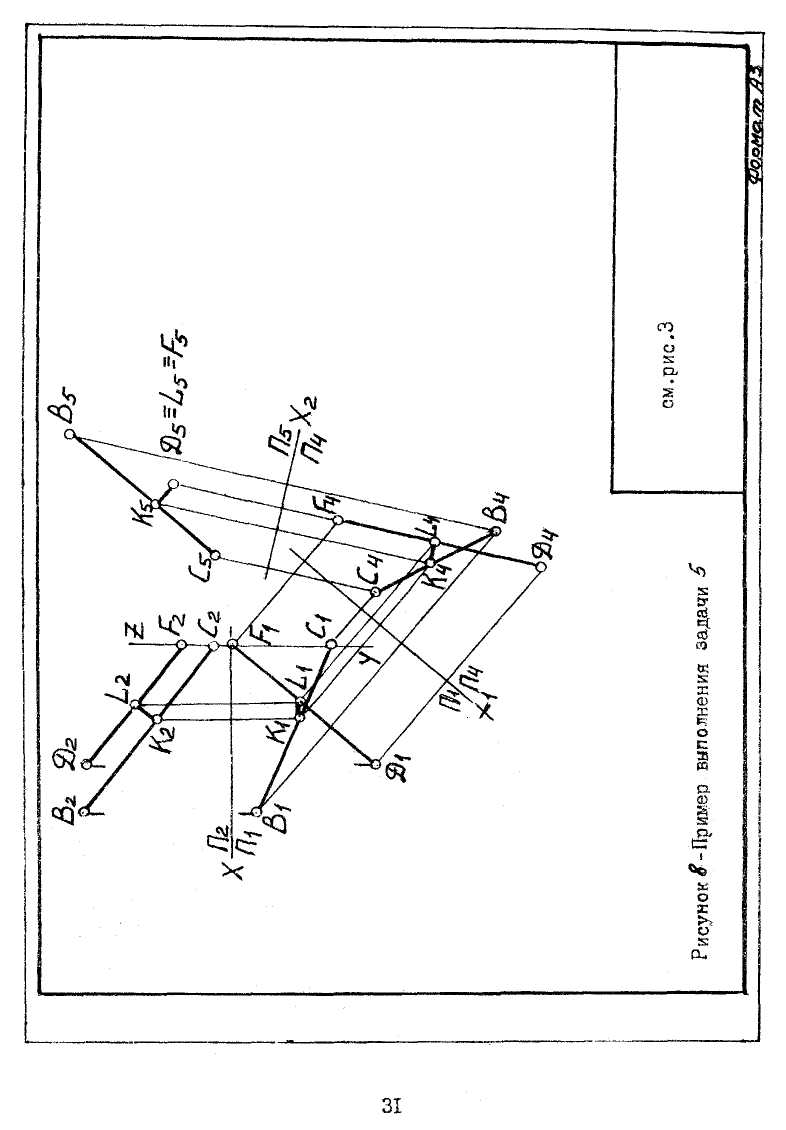
На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. В середине чертежного поля нанести оси координат, и из таблицы 1, согласно своему варианту, взять координаты точек С, В, D и F. Масштаб принять, исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа и точки не должны выходить за пределы чертежного листа.

Решение:

Кратчайшее расстояние между скрещивающимися прямыми можно измерить отрезком перпендикуляра к обеим прямым. Это обстоятельство дает возможность одну из прямых расположить перпендикулярно к какой-либо новой плоскости проекций, а отрезок перпендикуляра к обеим прямым окажется параллельным к новой плоскости проекций, т.е. прямую общего положения преобразовать в прямую уровня, а затем прямую уровня преобразовать в проецирующую прямую. При первичном преобразовании чертежа вводится плоскость проекций П₄, расположенная параллельно одной из прямых, например, DF и перпендикулярно к плоскости П₁ .На чертеже проводится новая ось проекций Х₁ параллельно горизонтальной проекций прямой DF, т.е. Х₁║ D₁F₁. Из соответствующих горизонтальных точек (D,F,В и С) проводится линия связи на новую ось проекций, и от точек пересечения откладываются на них в соответствующую сторону отрезки, равные расстоянию от П₂ до фронтальных проекций точек. При вторичном

преобразовании эпюра ( ) вводится новая плоскость проекций П₅ перпендикулярно к прямой DF и плоскости П₄. На чертеже проводится новая ось проекций Х₂ перпендикулярно D₄F₄, т.е. Х_{2 ┴} D₄F₄. Затем из соответствующих проекций точек D₄F₄ В₄ и С₄ проводятся перпендикуляры на ось проекций Х₂ и от точек пересечения откладываются на них в соответствующую сторону отрезки равные расстоянию от П₁ до горизонтальных проекций точек. Перпендикуляр LК(L₅К₅), опущенный из точки D₅ ≡ F₅ на прямую В₅С₅, определяет кратчайшее расстояние между скрещивающимися прямыми DF и ВС. Обратным построением (по стрелкам) но точке К₅ находится К₄ на В₄С₄; проекция К₄L₄ должна быть параллельна

32

оси проекций Х₂. Далее по К₄ и L₄ определяется К₁ и L₁на В₁C₁и D₁F₁и по ним К₂ и L₂ на В₂С₂ и D₂ F ₂.

Линии К₁L₁, К₂L₂, К₄L₄ и К₅L₅ следует показать основными сплошными линиями толщиной 1…1,5 мм красным цветом.

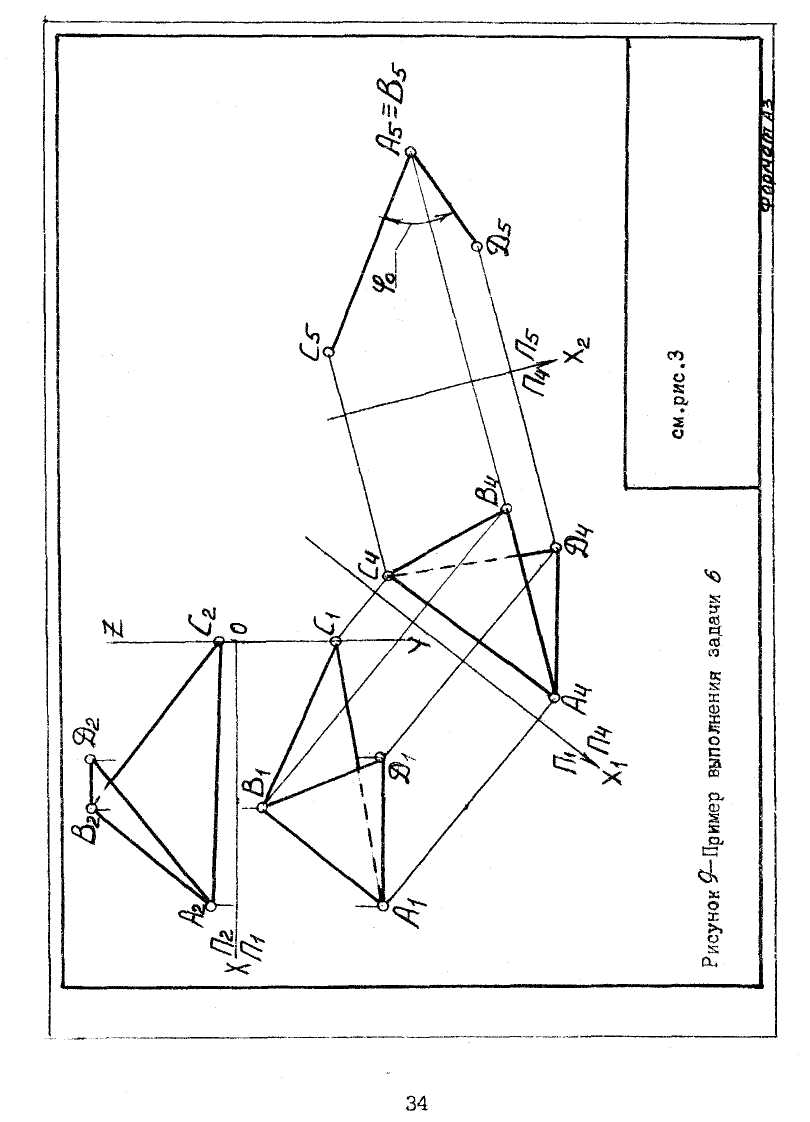
Задача № 6. Определить угол между гранями АВС и АВD при ребре АВ. Данные для своего варианта взять из таблицы 1. Пример выполнения задачи 6 приведен на рисунке 9.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. Следует выбрать исходное положение чертежа такое, чтобы графические построения помещались в пределах чертежного листа. Нанести оси координат и из таблицы 1, согласно своему варианту, взять координаты точек А, В, С и В. Масштаб принять, исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа.

Решение:

Двугранный угол измеряется линейным углом, полученным в пересечении граней двугранного угла плоскостью, перпендикулярной к обеим граням двугранного угла, а следовательно, и к линии их пересечения, т.е ребру АВ. Если это ребро АВ окажется перпендикулярным к какой-либо плоскости, например, плоскости П₅, то полученная на плоскости П₅ проекция двугранного угла будет выражать его линейный угол. Решение задачи следует выполнить при помощи способа замены плоскостей проекций. От системы ^П2/_П1 совершен переход к системе ^П4/_П1, где П₄ || АВ и П_{4 ┴} П_1, а на чертеже Х₁║А₁В_1. Затем от этой системы ^П4/_П1 выполнен переход к системе ^П4/_{П5 ,}где П_{5 ┴} АВ и

П_{5 ┴} П₄ ,а на чертеже- Х₂ ║А₄В₄. Проекции точек А₅, В₅ проецируются в точку. Отсюда следует, что в результате получили линейный угол фо.

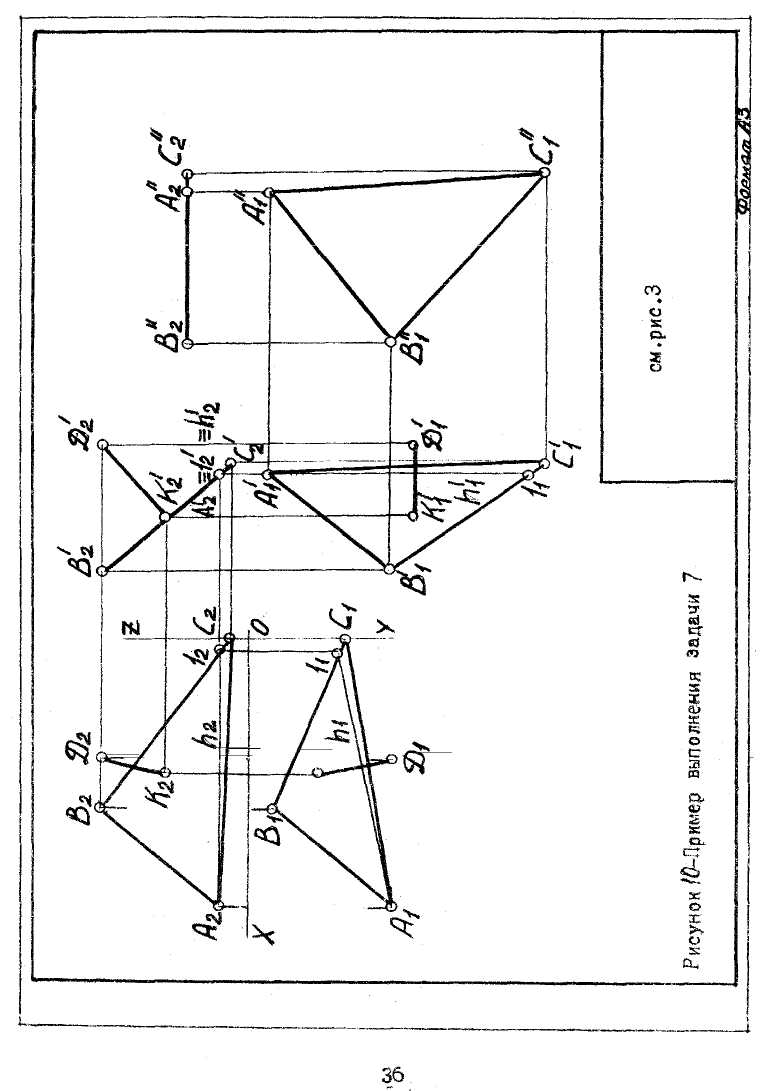
Задача 7. Определить расстояние от точки D до плоскости треугольника АВС и установить его истинную величину методом

плоскопараллельного перемещения. Исходные данные для своего варианта взять из таблицы 1. Пример выполнения задачи 7 приведен на рисунке 10.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. Следует выбрать исходное положение чертежа такое, чтобы графические построения помещались в пределах чертежного листа. В левой стороне нанести оси координат из таблицы 1. Согласно своему варианту взять координаты точек А, В, С и D. Масштаб принять исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа.

Решение:

Известно, что расстояние от точки до плоскости измеряется величиной перпендикуляра, проведенного из точки на плоскость. Это расстояние проецируется на какую-либо плоскость проекций в натуральную величину, если заданная плоскость перпендикулярна к плоскости проекций. Добиться такого положения можно, например, преобразуя чертеж способом плоскопараллельиого перемещения. Сущность этого способа заключается в том, что геометрические образы (элементы пространства) перемещаются параллельно относительно одной из плоскостей проекций, из общего положения в частное, при этом не меняя относительного расстояния между элементами входящими в геометрический образ. В соответствие с этим, проводится в плоскости треугольника АВС горизонталь h(h₁,h₂) и перемещаются все элементы пространства до тех пор, пока горизонталь h плоскости не станет перпендикулярна к плоскости П₂, т.е. проекция h₁ должна быть перпендикулярной к оси проекций X. Плоскость АВС переместилась в положение A'B'C'.Вэтом положении плоскость треугольника стала фронтально-проецирующей (A₁'B₁'C₁' A₂'B₂'C₂'), и расстояние К₂'D₂' от точки D до нее получится на плоскости проекций П₂ без искажения, равное натуральной величине. Затем следует переместить плоскость А'В'с' в положение А"В"С" (А₂"В₂"С₂", А₁"В₁"С₁") параллельное горизонтальной плоскости проекций, и устанавливается истинная величина треугольника — положение А₁"В₁"С₁".

35

Проекции К₁D₁,K₂D₂,K'₁D'₁,K'₂D'₂,A"₂B"₂C"₂ и A"₁B"₁C"₁ следует показать основными сплошными линиями красного цвета.

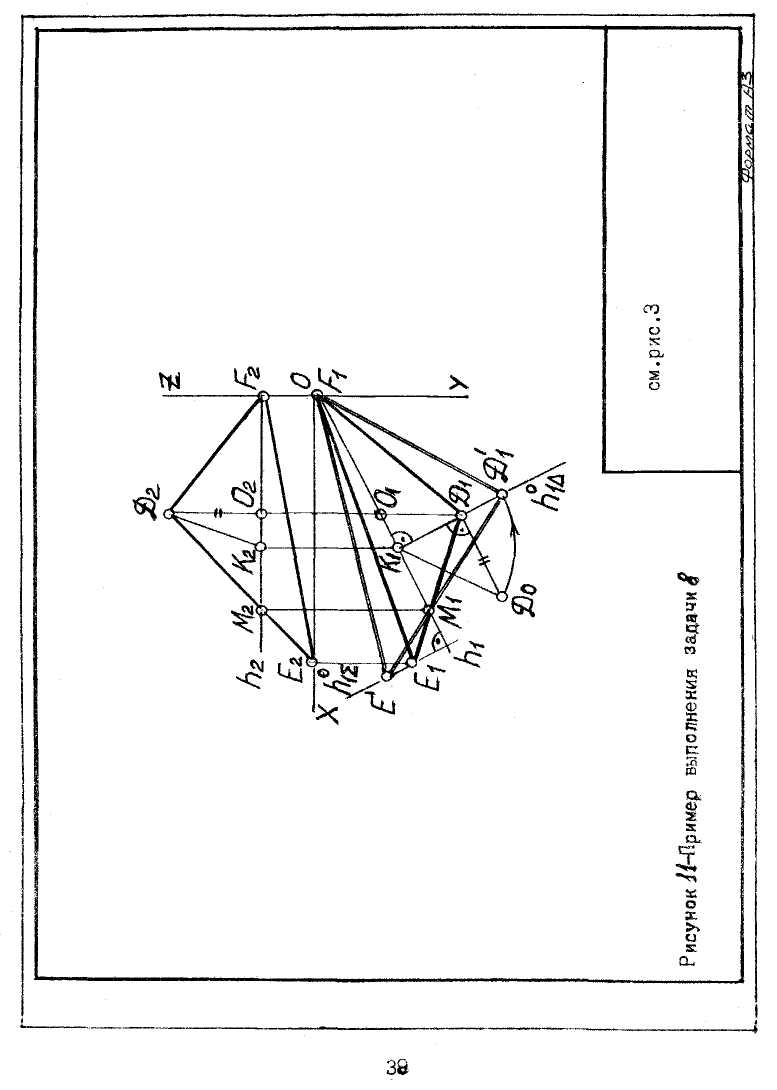
Задача № 8. Установить натуральную форму треугольника DЕF при помощи вращения вокруг горизонтали (фронтали). Исходные данные для своего варианта взять из таблицы 1. Пример выполнения задачи 8 приведен на рисунке 11.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. Следует выбрать исходное положение чертежа такое, чтобы графические построения помещались в пределах чертежного листа. В середине листа нанести оси координат, и из таблицы 1,согласно своему варианту, взять координаты точек D, Е и F. Масштаб принять, исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа.

Решение:

В плоскости треугольника DЕF построить ось вращения, например, горизонталь h(h₁,h₂) . Провести через вершину D плоскость вращения ∆, перпендикулярную к оси вращения, и отметить центр К(К₂,К₁) вращения и проекции радиуса DК(D₂K₂,D₁K₁) вращения. Определить натуральную величину радиуса К₁Dо вращения. Раствором циркуля, равным К₁Dо, найти новую проекцию точки D'(D₁'). Точка Е (E₁') определяется при выполнении следующего построения:

а) провести из точки D₁' прямую через точку М₁(М₁=h₁∩D₁E₁) до пересечения с линией, по которой перемещается точка Е₁ при вращении треугольника вокруг горизонтали h в плоскости Σ, перпендикулярной к оси вращения h; б)соединить точки E'₁,D'₁,F'₁.Получится треугольник E'₁D'₁F'₁ равный натуральной величине. Линии этого треугольника показать сплошными линиями красного цвета.

Задача № 9. Забои выработок А и В начав движение одновременно с равными скоростями встречаются в точке Т. Зная по одной проекции направления движения забоев выработок, найти точку встречи. Исходные

37

данные дня своего варианта взять из таблицы 2. Пример выполнения задачи 9 приведен на рисунке 12.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. Следует выбрать исходное положение осей координат такое, чтобы графические построения помещались в пределах чертежной рамки. Согласно своему варианту, из таблицы 2 взять координаты точек А и В и углы ε₀, φ_о проекций направления движения забоев и построить исходное положение элементов пространства. Масштаб принять, исходя из условия, что комплексный чертеж будет занимать не менее ¾ чертежного листа.

Решение:

Так как длины горных выработок АТ и ВТ равны, то направление движения точек А и В можно представить в виде боковых сторон равнобедренного треугольника АТВ с основанием АВ. Следовательно, точка встречи Т как вершина равнобедренного треугольника находится в плоскости Σ(h∩f),, перпендикулярной основанию АВ и проходящей через его середину. Через точку К проводится плоскость Σ(h∩f) перпендикулярно прямой АВ, а именно: фронтальную проекцию фронтали (f₂) провести перпендикулярно к фронтальной проекции прямой АВ(f_{2 ┴} А₂В₂), горизонтальная проекция фронтали f₁ проводится параллельно оси проекций X (f₁ || ОХ); горизонтальную проекцию горизонтали (h₂) провести перпендикулярно к горизонтальной проекции прямой АВ(h_{1 ┴} A₁B₁), а фронтальная проекция горизонтали (h₂) проводится параллельно оси проекций X (h₂ || ОХ). Заключить одну из проекций направления движения забоев выработок, например, во фронтально-проецирующую плоскость ∆(∆ _┴ П₂). Далее находить линию 1-2 пересечения плоскости ∆ с плоскостью Σ(h∩f).Определяется точка Т(Т_1,Т₂) пересечения линии 1-2 с боковой стороной проходящей через точку В.

Проекции А₂Т₂, В₂Т₂, А₁T₁ и В₁Т₁ направления движения горных выработок показать двойными тонкими линиями красного цвета.

39

Задача № 1О Построить линию пересечения пирамиды с прямой призмой. Данные для своего варианта взять из таблицы 3. Пример выполнения задачи 10 приведен на рисунке 13.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. Нанести оси координат из таблицы 3, согласно своему варианту, взять координаты точек А, В, С, D, Е, К, Fи U и высоту призмы h. Масштаб принять 1:1.

Решение:

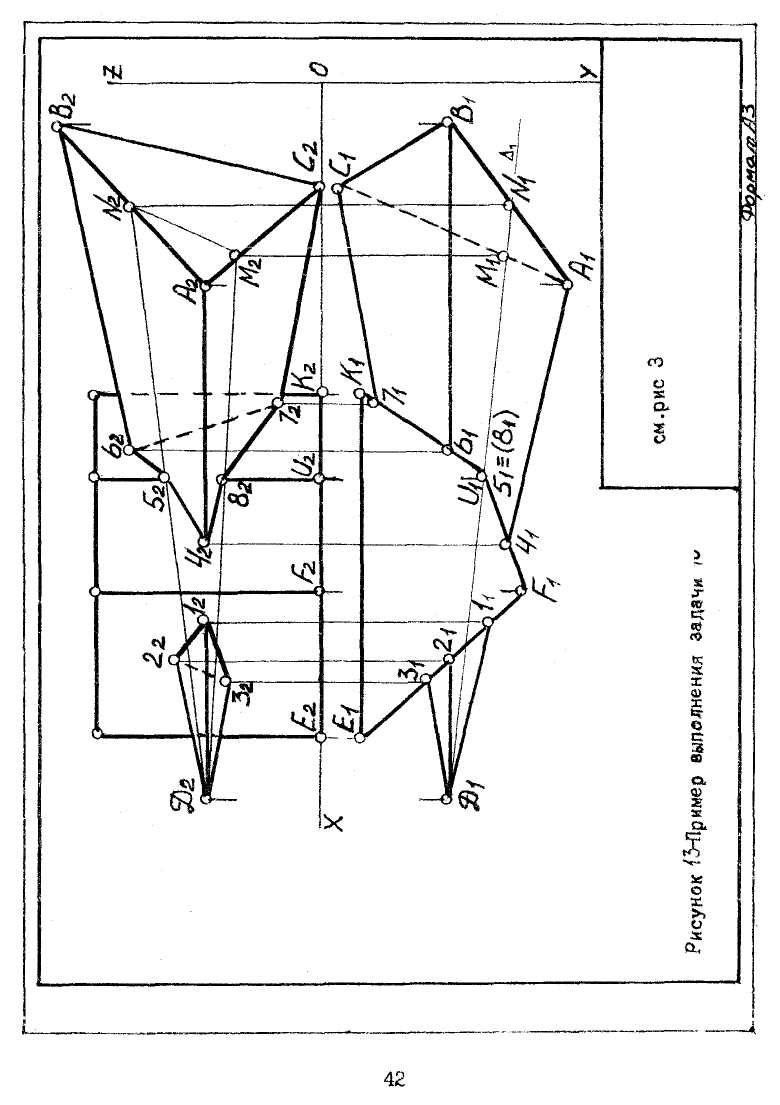
Поскольку грани призмы ЕFUКЕ горизонтально проецирующие, то точки 1,2,3,4,6 и 7 пересечения граней фигур находятся без дополнительных построений на горизонтальной плоскости, затем по первому закону проекционной связи определяются фронтальные проекции этих точек. Для нахождения точек 5 и 8, лежащих на горизонтально проецируемом ребре U, следует воспользоваться вспомогательной горизонтально проецирующей плоскостью ∆. Фронтальные проекции точек 5 и 8 лежат на граничных точках фронтальных проекций сечения DMN и ребра U₃, т.е.Uc∆; ∆∩DACB=D,M,N∩U = 5,8. Соединяются точки 1,2,3,1 и 4,5,6,7,8,4 (1₂2₂З₂1₂) и (4₂5₂б₂7₂8₂4₂) ломаными линиями, и получается искомая линия пересечения. Видимыми являются только те стороны многоугольника пересечения, которые принадлежат видимым граням многогранников.

Их следует показать основными сплошными линиями толщиной 1,5 мм красного цвета, невидимые отрезки пространственной ломаной показать штриховыми линиями красного цвета.

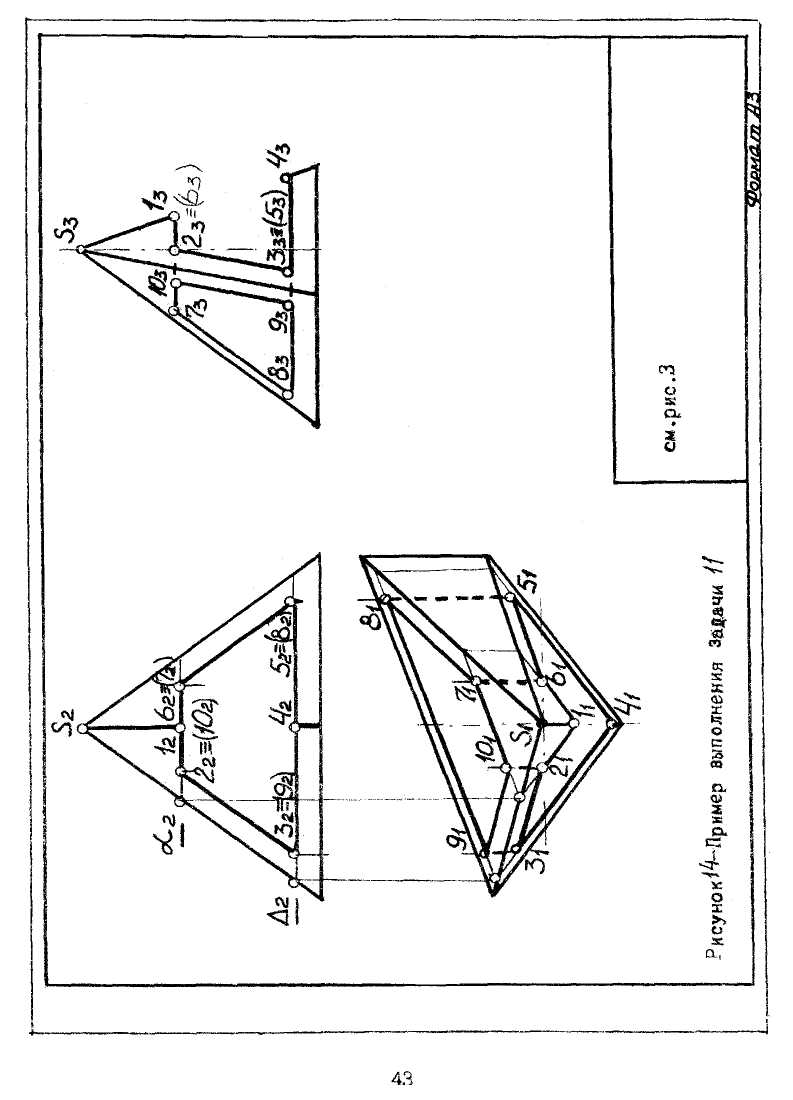
Задача № 11. На трeхпроекционном чертеже построить недостающие проекции, линии взаимного пересечения поверхностей пирамиды и сквозного призматического отверстия. Данные для своего варианта взять из таблицы 4. Пример выполнения задачи 11 приведен на рисунке 14.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. Из таблицы 4,согласно своему варианту,взять упрощенный чертеж фигуры и выяснить его в соответствии с разделом 2 .

41

Решение:

Для определения линии взаимного пересечения поверхностей следует использовать метод секущих плоскостей. При пересечении пирамиды горизонтальными плоскостями уровня пирамида будет рассекаться по замкнутой ломаной линии подобной основанию. В данной задаче одна из проекций линии пересечения а именно, фронтальная, известна, так как она сливается с фронтальной проекцией боковой поверхности призмы. Это значительно упрощает построение: оно сводится к нахождению горизонтальных проекций точек, принадлежащих поверхности пирамиды, по их фронтальным проекциям, а именно: делится линия призмы на ряд точек - (1,2,3,4,5,6) и (7,8,9,10). На уровне точек 1,2,6,7 и 10 проводится плоскость α _┴ П₁, и находятся характерные точки 1,2,6,7,10 (1₂,2₂,б₂,7₂,10₂; 1₁,2₁,6₁,7₁,10₁) пересечения ребер призмы с поверхностью пирамиды. Проводится секущая плоскость ∆ (∆ || П₁) и определяются характерные точки 3,4,5,8,9 (3₂,4₂,5₂,8₂,9₂; 3₁,4₁,5₁,8₁,9₁) пересечения боковой грани призмы с поверхностью пирамиды. Профильная проекция линии взаимного пересечения строится по проекционным линиям связи.

Выдимые линии взаимного пересечения следует показать основными сплошными линиями, а невидимые - штриховыми красного цвета.

Задача № 12. На трехпроекционном чертеже построить недостающие проекции, линии взаимного пересечения поверхностей конуса (название фигуры своего варианта) и сквозного призматического отверстия. Данные для своего варианта взять из таблицы 5. Пример выполнения задачи 12 приведен на рисунке 15.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104-68. Из таблицы 5, согласно своему варианту, взять упрощенный чертеж фигуры и построить его в соответствии с разделом 2.

Решение:

Для определения линии взаимного пересечения поверхностей следует использовать метод секущих плоскостей, заключающийся в проведении

44

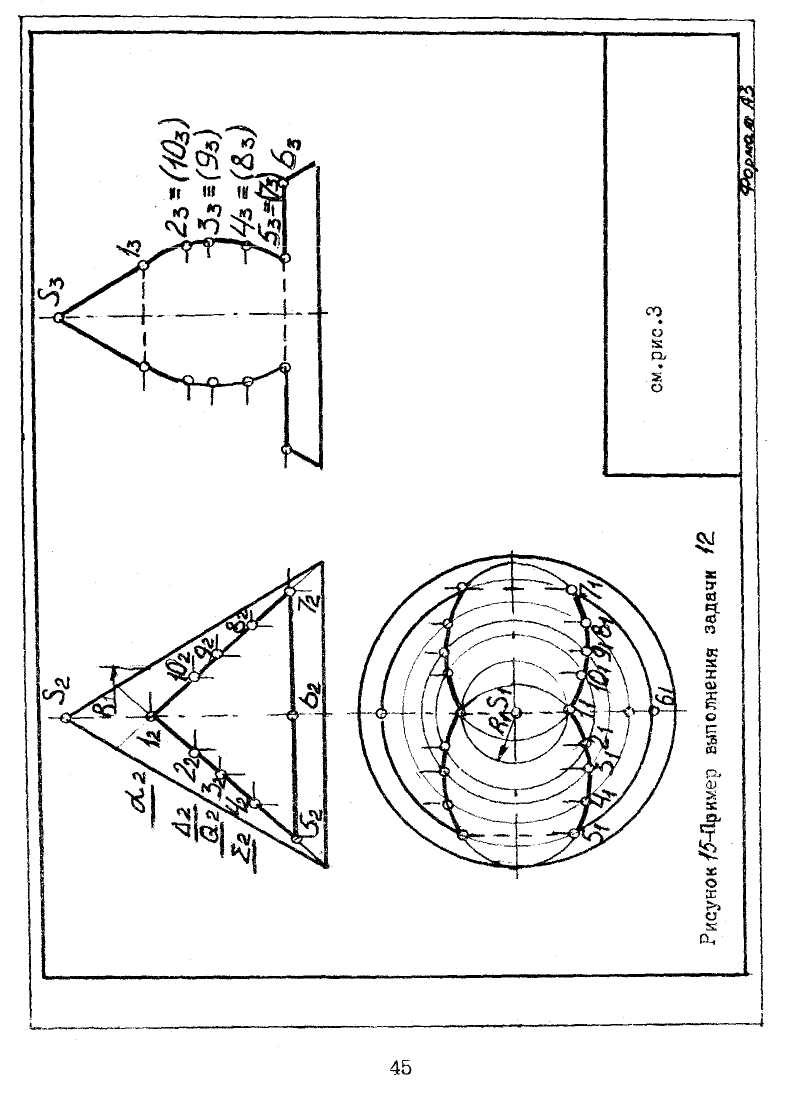
плоскостей, пересекающих обе поверхности по наиболее простым линиям -прямым и окружностям. Пересечения каждой пары этих линий дают точки искомой кривой - линии взаимного пересечения поверхностей (линии перехода). Простейшие формы сечений призмы и конуса имеют место при пересечении обеих поверхностей горизонтальными плоскостями уровня. При этом конус будет рассекаться по окружностям, а призма по прямым, образующим призмы. В данной задаче одна из проекций линии пересечения, а именно, фронтальная известна, так как она сливается с фронтальной проекцией боковой поверхности призмы. Это значительно упрощает построение: оно сводится к нахождению горизонтальных проекций точек, принадлежащих поверхности конуса, по их фронтальным проекциям, а именно: делится линия призмы на ряд точек - (1,2,3,4,5); (5,6,7) и (7,8,9,10). Одним обстоятельством, имеющим большое значение в построении является то, что получаемая линия пересечения известна.. Две боковые грани призмы пересекают поверхность конуса по дуге эллипса (1 -5) и (1-7), а третья грань призмы пересекает - по дуге окружности ( 5-7). Точки 3 и 9 являются малыми осями эллипсов. Точки 1,5,6,7 являются опорными, а точки 2,4,8,10 - промежуточными. Для нахождения горизонтальной точки 1 и ей симметричной проводится вспомогательная плоскость α (α || П₁) через ребро призмы. На горизонтальной плоскости проекций радиусом R₁ строится окружность. От фронтальной проекции точки 1 опускается линия связи (или линия пересечения призмы с плоскостью α). По двум проекциям строится профильная проекция точки 1 по проекционным законам линий связи. Другие проекции точек 3,4,5,6,7,8,9 и 10 определяются аналогично. Полученные проекции точек соединить криволинейной линией, и получается искомая линия пересечения.

Видимые проекции линий взаимного пересечения показать сплошными линиями, а невидимые - штриховыми красного цвета. Профильные проекции точек 7,8,9 и 10 заключить в скобки как невидимые элементы образа дуги эллипса (1-10-9-8-7).

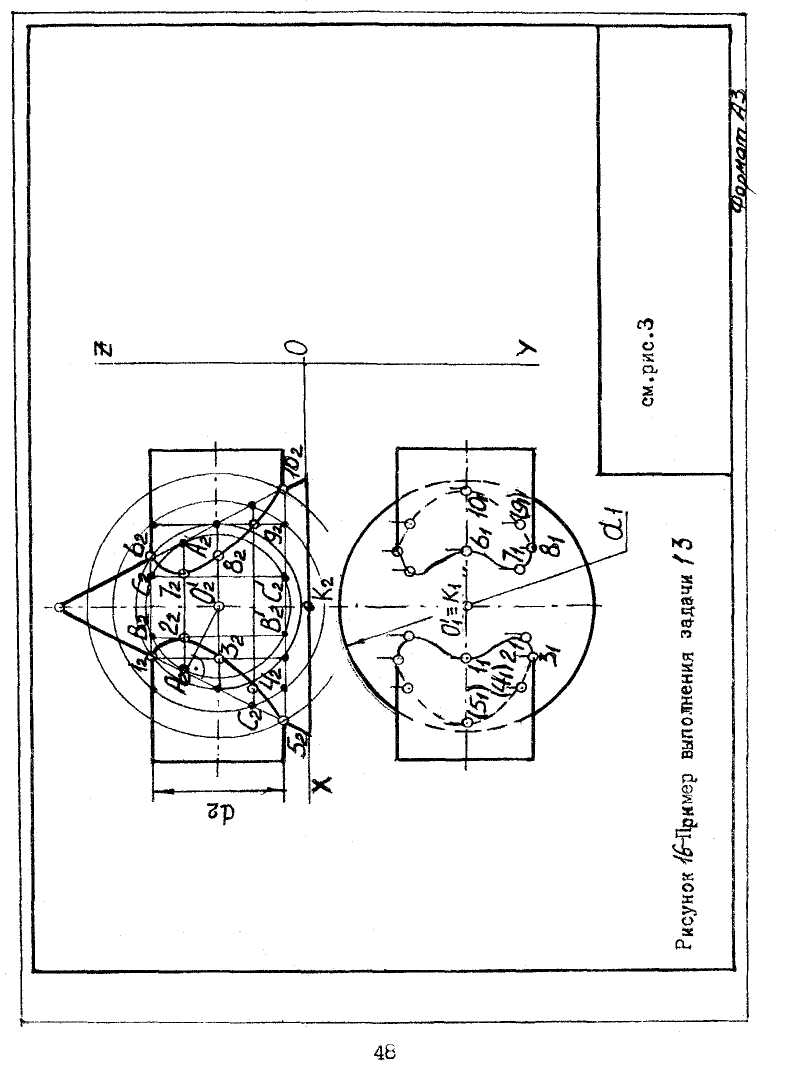
Задача № 13. Построить линию взаимного пересечения конуса вращения с цилиндром вращения. Оси поверхностей вращения взаимно

46

перпендикулярны, пересекаются и расположены параллельно фронтальной плоскости проекций (П₂).

Данные для своего варианта взять из таблицы 6. Пример выполнения задачи 13 приведен на рисунке 16.

Последовательность решения и оформления задачи.

На чертежном листе формата АЗ выполнить чертежную рамку по ГОСТ 2.301-68 и основную надпись по ГОСТ 2.104—68. Нанести оси координат и из таблицы 6, согласно своему варианту, взять величины, которыми задаются поверхности конуса вращения и цилиндра вращения, а именно: координаты точек К и О; диаметр цилиндра, диаметр основания конуса.; высота h конуса. Масштаб принять 1:1.

Решение:

Для решения задачи следует применить метод концентрических сфер. Принимается точка О(О₁,О₂) пересечения осей цилиндра и конуса за центр вспомогательных сферических поверхностей. Проводится ряд концентрических сфер с центром в точке (О_1,О₂). При этом радиус наибольшей сферы R_mах равен О₂5₂, т.е. расстоянию до наиболее удаленной точки пересечения заданных поверхностей, а радиус наименьшей сферы R_min - радиусу сферы, вписываемой в поверхность вращения конуса. Если принять R_min - радиус сферы, вписываемой в поверхность цилиндра этой задачи, то линии пересечения конуса данной сферы не будет.

В каждом конкретном случае, между наибольшей сферой и наименьшей сферой строится две, три или четыре сферы. Вспомогательные сферы пересекаются с каждой из заданных поверхностей по окружностям. Фронтальные поверхности окружностей изображаются отрезками прямых линий проецируемым и на одну из плоскостей проекций в виде отрезков прямых, например, А₂А'₂>В₂В'₂ в пересечении которых получаются фронтальные проекции (2₂ и 7₂) точек 2 и 7, общие для обеих поверхностей. Пользуясь вспомогательными секущими плоскостями (они не показаны), определяются горизонтальные проекции 2₁ и 7₁ точек 2 и 7. Аналогично, изменяя только радиусы сферы, получается еще ряд точек (3₂,4₂,5₂,8₂,9₂;3₁,4₁,5₁,8₁,9₁,). Точки (1₂,5₂,6₂,10₂;1₁,5₁,6₁,10₁).находятся обычным построением. Все полученные точки соединить кривой линией. Получается искомая линия взаимного пересечения поверхностей.

47

Видимые линии взаимного пересечения обвести основными сплошными линиями, невидимые линии - штриховыми красного цвета.

Перечень экзаменационных вопросов по начертательной геометрии приведен в приложениях.

49