Лабораторно-практическое занятие № 4 исследование неразветвленной электрической цепи переменного тока

Типовые задачи

Задача 4.1. Заданы параметры элементов электрической цепи (рис. 4.1) и входное напряжение U_ВХ=141sin 314t В.

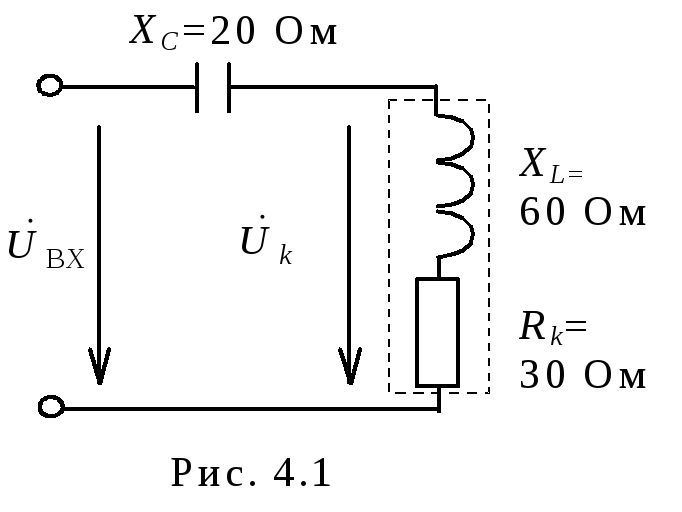
Определить напряжение на катушке и построить векторную диаграмму тока и напряжений, используя данные таблицы 4.1.

Решение

Расчет цепи проведем, используя комплексный метод анализа цепей синусоидального тока.

Представим все электрические величины (,Z_C , Z_L , Z_R) в комплексной форме (рис. 4.2) и определим комплексный ток цепи

=100e^j0 B,

Z_C = - j X_C ; Z_L = j X_L ; Z_R = R_K,

где – действующее значение входного напряжения U_ВХ, В.

Полное комплексное сопротивление цепи с последовательно соединенными элементами Z_ВХ равно сумме комплексных сопротивлений этих элементов

Z_ВХ = Z_C + Z_L + Z_R = - j X_C + j X_L + R_k =

= R_k +j (X_L - X_C ) = 30 +j (60 - 20) = 30+j40 Ом.

В показательной форме записи

Z_ВХ = Z e^j = 50e^j53 Ом ;

(Z Ом;

53,1353).

По закону Ома определим величину комплексного тока цепи

= /Z_ВХ =100e^j0/(5e^j53) = (100 /5)е ^j(0–53) = 2e^-j53 A.

Комплексное напряжение на катушке также можно определить по закону Ома, но предварительно следует определить комплексное сопротивление катушкиZ_k

Z_k = R_k +j X_L = 30+j 60 Ом,

или в показательной форме записи

Z_k= Z_k e^jk = 67e^{j 63,4} Ом

(Z_k Ом;

) .

Тогда =Z_k = 67e^j63,4 2e ^-j53= (672)e^{j(63,4-53)} = 134 e^j10,4 В.

Соответственно мгновенное значение напряжения на катушке

u_k = 134 sin 314t = 189 sin 314t В.

Векторные диаграммы напряжений и тока в неразветвленной цепи синусоидального тока (рис. 4.3) строят на комплексной плоскости в соответствии с уравнением, составленным по второму закону Кирхгофа (4.1) и с учетом фазовых сдвигов напряжений ,,и токаво времени

(4.1)

Здесь

= Z_R = R_k = 302e^-j53= 60e^-j53 В,

= Z_C = (- j X_C)= (- j202e^-j53) = 20е ^-j90 2e ^-j53 = 40 е^–j143 B,

= Z_L = (j X_L) = (j 60)  2e^-j53 = 60 е^-j902e ^-j53 = 120e^j37 B.

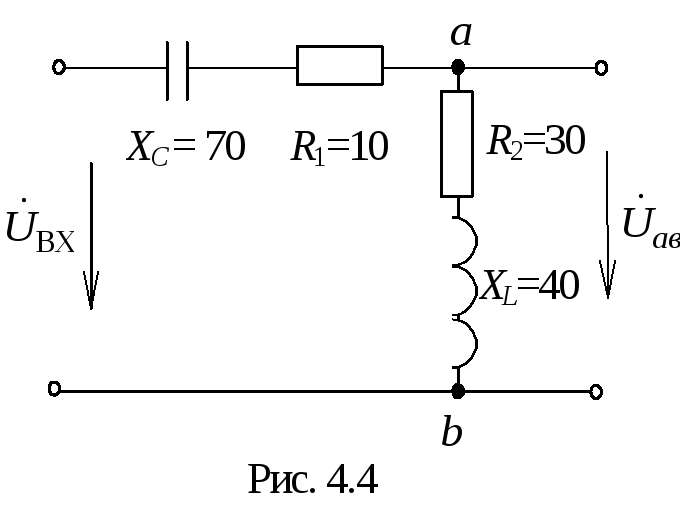
Задача 4.2. Заданы параметры элементов электрической цепи (активные и реактивные сопротивления заданы в Омах) и входное напряжение U_ВХ=50 В (рис. 4.4). Определить напряжение , потребляемое активную и полную мощности, используя данные таблицы 4.2. Построить векторную диаграмму тока и напряжений.

Решение

Расчет цепи ведем комплексным методом.

Алгоритм расчета имеет следующий вид: представляем все электрические величины (,Z_C , Z_L , Z_R1, Z_R2) в комплексной форме и определяем комплексный ток цепи , далее определяем комплексное напряжениена участке цепи (a – b):

=/Z_ВХ, =Z_аb .

Так как задано действующее значение входного напряжения, то, принимая его начальную фазу _Uвх равной нулю, запишем :

=50e^j0 B.

Полное комплексное сопротивление цепи с последовательным соединением элементов Z_BX равно сумме комплексных сопротивлений этих элементов

Z_BX = Z_C + Z_R1+ Z_R2 + Z_L = - j X_C + R₁ + R₂ + j X_L =

= R₁ + R₂ + j (X_L - X_C ) = R + j X = 40 – j30 Ом .

В показательной форме записи Z_ВХ = Z e^j

Z Ом;

- 36,87  -37;

Z_ВХ = Z e^j = 50 e^-j37 Ом.

Определяем комплексный ток цепи

=/ Z_ВХ = 50e^j0/ 50e^-j37= 1e^j37 А.

Комплексное сопротивление Z_аb на участке цепи (a – b):

Z_аb = Z_R2 + Z_L = R₂ + j X_L = 30 + j40 Ом;

Z_аb = Z_аbe^jаb =50e^j53 Ом;

(Z_аb=50 Ом,_аb=53,1353).

Находим комплексное напряжение

=  Z_аb =1e ^j3750e^j53 = 1 50 ^{j(37+ 53)} = 50e^j90 В.

Определим активную мощность цепи P

P = UI cos  = 501cos (-37) = 40 Вт.

Активную мощность цепи можно определить и как

P =(R₁ + R₂ )I² = 1²(10 + 30 ) = 40 Вт.

Полная мощность цепи S равна:

S = UI = 501 = 50 ВА.

Построим векторную диаграмму напряжений и тока цепи в соответствии с уравнением второго закона Кирхгофа и с учетом фазовых сдвигов напряжений ,,,,,и токаво времени (рис. 4.5):

(4.2)

Найдем слагаемые уравнения (4.2) – комплексные напряжения на элементах цепи:

= Z_C =(- j X_C ) = (- j70) 1e^j37 = 70е^–j90 1e^j37= 70е^–j53 B;

= R₁ = 101e^j37 = 10e^j37 В; =R₂ = 401e^j37=40e^j37 В;

= Z_L = (j X_L)= ( j 40)  1e^j37= 40е^j90 1e^j37 = 40e^j127 B.

Располагаем вектор токав выбранном масштабе под углом_I к оси действительных чисел, откладывая этот угол 37 против часовой стрелки (как и все положительные значения углов).

Геометрическая сумма всех векторов равна вектору входного напряжения, который располагается вдоль оси вещественных чисел (начальная фаза равна нулю).

Построение на векторной диаграмме векторов напряжений производим последовательно – к концу одного вектора прикладываем начало следующего вектора в соответствии с уравнением (4.2).

Векторы напряжений на резистивных элементах исовпадают по фазе с током и располагаются параллельно вектору. Вектор напряжения на емкостном элементеотстает по фазе от векторана 90, а вектор напряжения на индуктивном элементе опережает по фазе вектор токана 90. Вектор напряжения определяется также в соответствии со вторым законом Кирхгофа как

и располагается перпендикулярно оси вещественных чисел (_Uаb = 90).

Задача 4.3. В цепи с параметрами, заданными в Омах, протекает ток (рис. 4.6). Определить, используя данные таблицы 4.3, между какими точками в этой цепи будет наблюдаться наибольшее напряжение. Задачу рекомендуется решать с помощью векторной диаграммы.

Решение

Проведем расчет двумя способами.

Первоначально рассмотрим следующий алгоритм расчета цепи: представляем все электрические величины (,Z_i ) в комплексной форме, определяем полное комплексное сопротивление цепи Z_mn и далее определяем комплексное напряжение на входе, а также комплексные напряжения на отдельных участках цепи:

= Z_mn ; =Z_ij. (4.3)

Запишем комплексное значение тока в цепи. Модуль комплексного тока равен действующему значению тока I = I_m/2 = 1A, а аргумент комплексного числа равен начальной фазе _i =20;

= =1e ^j20 А.

Полное комплексное сопротивление цепи с последовательным соединением элементов Z_mn равно сумме комплексных сопротивлений этих элементов

Z_mn = j X_L1 + R₁ + R₂ - j X_{C 1} +j X_L2 + R₃ - j X_{C 2} =

= R₁ + R₂ + R₃ + j(X_L1+X_L2 - X_C1 -X_{C 2}) = R + j X = 24 – j2 Ом .