1.Движение тела по окружности с постоянной по модулю скорости.

Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.

Положение тела на окружности определяется радиусом-вектором , проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).

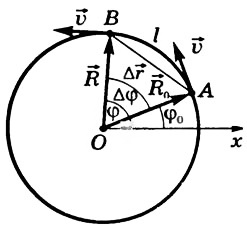
Рис. 1

За время Δt тело, двигаясь из точки А в точку В, совершает перемещение , равное хорде АВ, и проходит путь, равный длине дуги l.

Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.

Скорость движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:

Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:

В СИ единицей угловой скорости является радиан в секунду (рад/с).

При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.

Положение тела можно определить, если известен модуль радиуса-вектора и угол φ, который он составляет с осью Ox (угловая координата). Если в начальный момент времени t₀ = 0 угловая координата равна φ₀, а в момент времени t она равна φ, то угол поворота Δφ радиуса-вектора за время равен . Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:

Оно позволяет определить положение тела в любой момент времени t. Учитывая, что , получаем:

— формула связи между линейной и угловой скоростью.

Промежуток времени Τ, в течение которого тело совершает один полный оборот, называется периодом вращения:

где N — число оборотов, совершенных телом за время Δt.

За время Δt = Τ тело проходит путь . Следовательно,

Величина ν, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:

Следовательно,

Билет №4

1.Взаимодействие тел.

Взаимодействие тел. Опыт показывает, что при сближении тел (или систем тел) характер их поведения меняется. Поскольку эти изменения носят взаимный характер, говорят, что тела взаимодействуют друг с другом. При разведении тел на очень большие расстояния (на бесконечность) все известные на сегодняшний день взаимодействия исчезают. Галилей первым дал правильный ответ на вопрос, какое движение характерно для свободных (т.е. не взаимодействующих тел). Вопреки существующему тогда мнению, что свободные тела стремятся к состоянию покоя, он утверждал, что при отсутствии взаимодействия тела находятся в состоянии равномерного движения, включающего покой как частный случай. Инерциальные системы отсчета.  В рамках формального математического подхода, реализуемого в кинематике, утверждение Галилея выглядит бессмысленным, поскольку равномерное в одной системе отсчета движение может оказаться ускоренным в другой, которая ничем не хуже исходной. Наличие взаимодействия позволяет выделить особый класс систем отсчета, в которых свободные тела движутся без ускорения (в этих системах большинство законов природы имеют наиболее простую форму). Такие системы называются инерциальными. Все инерциальные системы эквивалентны друг другу, в любой из них законы механики проявляются одинаково. Это свойство было также отмечено Галилеем в сформулированном им принципе относительности: никаким механическим опытом в замкнутой (т.е. не сообщающейся с внешним миром) системе отсчета невозможно установить покоится ли она или равномерно движется. Любая система отсчета, равномерно движущаяся относительно инерциальной тоже является инерциальной. Между инерциальными и неинерциальными системами отсчета существует принципиальное отличие: находящийся в замкнутой системе наблюдатель способен установить факт движения с ускорением последних, не выглядывая наружу(напр. при разгоне самолета пассажиры ощущают, что их вдавливает в кресла).