Упражнение 4. Для каждого из 4-х приведенных ниже интегралов существует подстановка сводящая его к табличному. Укажите для каждого интеграла нужную подстановку

,

.

§ 4. Метод интегрирования по частям

Метод интегрирования по частям пользуется не меньшей популярностью, чем метод замены. Существует немало неопределенных интегралов, которые берутся в элементарных функциях только с помощью метода интегрирования по частям. Метод интегрирования по частям базируется на следующем простом утверждении.

Теорема 3. Пусть каждая из функций u = u(x) и v = v(x) определена и дифференцируема на (a,b) и функция v(x)u'(x) имеет первообразную на (a,b). Тогда на (a,b) существует первообразная для функции v'(x)u(x) , причем справедлива формула

.

В силу инвариантности формы первого дифференциала эту формулу можно переписать, убрав для краткости записи переменную х :

.

► Нам потребуется формула для производной произведения двух функций.

.

Умножим это равенство на dx и возьмем интеграл от обеих частей вновь полученного равенства. На основании свойства 2 имеем . Так как по условию функция v(x)u'(x) имеет первообразную на (a,b) и учитывая третье свойство интеграла, получаем, что функция v'(x)u(x) также имеет первообразную на (a,b) .

.

Остается перенести в левую часть, и мы придем к требуемой формуле. Доказательство теоремы 3 закончено. ◄

Таким образом, метод по частям сводит вопрос о вычислении интеграла к вычислению интеграла , который в ряде конкретных случаев довольно легко вычисляется. Эти "конкретные случаи" могут быть (чисто символически) разбиты на следующие четыре группы:

1. В первую группу обычно относят интегралы вида , где – полином n-й степени , а Q(x) - некоторые «твердые» функции - a^x, sinx, cosx или другие, которые при дифференцировании переходят «сами в себя». Интегралы этой группы берутся n-кратным применением метода по частям. Рассмотрим пример.

= = - = – + C.

В только что рассмотренном примере в качестве «твердой» выступала самая «твердая» функция (при дифференцировании она переходит сама в себя) , а полином имел первую степень, поэтому оказалось достаточно разового применения метода по частям. Если полином имеет более высокую степень, то интегрирование по частям следует применить столько раз, какова степень полинома

.

После первого интегрирования степень полинома уменьшилась на единицу. Осталось применить формулу интегрирования по частям еще раз к интегралу

.

2. Во вторую группу относят интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций: lgx, arcsinx, arctgx,... при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции. Причем произведение этой известной функции на производную от вышеуказанных функций lgx, arcsinx, arctgx,... легко интегрируется.

Обычно, в качестве иллюстрации, предлагается нижеследующий пример:

3. К третьей группе относятся интегралы вида , ,... Это так называемая группа циклических интегралов. Для вычисления интегралов этой группы сам интеграл берется за некоторую переменную, например, I. После чего проводится двукратное (или n-кратное) интегрирование по частям, и для переменной I получается линейное уравнение. Стандартный пример на эту тему:

; возьмем

тогда

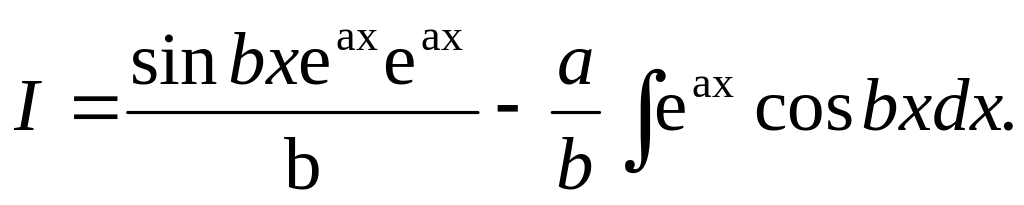
Для вычисления последнего интеграла еще раз применим формулу интегрирования по частям , полагая на этот раз Получим .

Таким образом, посредством двукратного интегрирования I по частям мы получили для интеграла I линейное уравнение первого порядка. Из этого уравнения находим:

+ С.

4. К четвертой группе относятся интегралы, для вычисления которых выводятся рекуррентные соотношения. Вычислим важный для дальнейшего интеграл .

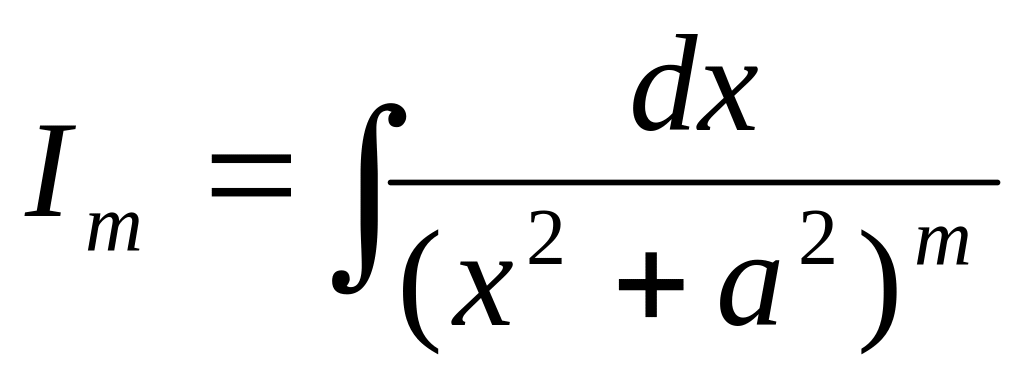Отметим сразу , что для m=1 вышеуказанный интеграл легко берется в элементарных функциях с помощью метода замены:

.

Мы легко вычислим I₂ , если будем знать, как I₂ выражается через I_{1 ,} и соответственно мы легко найдем I₃ , если будем знать, как I₃ выражается через I_2.

Теперь наша задача указать формулу, которая интеграл I_m выражает через интеграл I_m-1 :

.

Для вычисления последнего интеграла применим формулу интегрирования по частям, полагая в ней u = x , . Получим du = dx , , .

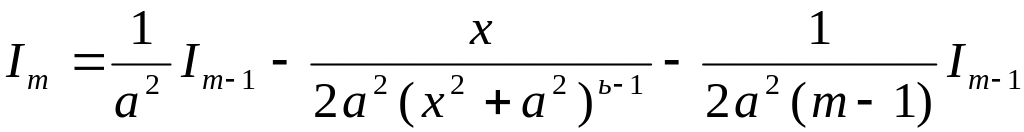Из последнего равенства получим рекуррентную формулу.

.

Так как вычислен интеграл I₁ , то с помощью последней формулы можно шаг за шагом вычислить I_m для произвольного m.

Конечно, указанные четыре группы не исчерпывают всех без исключения интегралов, берущихся посредством интегрирования по частям. Тем не менее они охватывают все предлагаемые в вузовском курсе интегралы (берущиеся методом по частям) и дают конкретные рекомендации к взятию этих интегралов.

Упражнение 5. Привести пример интеграла, который можно вычислить только методом интегрирования по частям.

Упражнение 6. (см. [17], c.32) Доказать обобщенную формулу интегрирования по частям. Пусть функции u(x) и v(x) имеют в рассматриваемом промежутке непрерывные производные до порядка (n + 1) включительно. Тогда справедлива формула