
- •Наращение
- •Дисконтирование
- •1.2. Номинальная и эффективная ставки
- •1.3. Эквивалентные процентные ставки
- •1.4. Финансовая эквивалентность обязательств
- •1.5. Учет инфляции
- •1.6. Постоянные финансовые ренты Виды потоков платежей и их основные параметры
- •Наращенная сумма и современная стоимость постоянной ренты постнумерандо (на примере годовой ренты)
- •1.7. Планирование погашения долгосрочной задолженности Расходы по обслуживанию долга
- •Создание погасительного фонда
- •Погашение долга в рассрочку
- •1.8. Оценка финансовой эффективности производственных инвестиций Характеристика эффективности производственных инвестиций
- •Чистый приведенный доход
- •Внутренняя норма доходности
- •Срок окупаемости
- •Индекс доходности
- •2. Математические основы финансового анализа в условиях риска и неопределенности
- •2.1. Риски и их измерители
- •2.2. Функция полезности дохода
- •2.3. Снижение риска
- •2.4. Виды ценных бумаг. Доходность ценных бумаг
Конспект лекций
1. Основы финансовых вычислений
1.1. Наращение и дисконтирование
Учет фактора времени в финансовом анализе
Система финансов построена на основе теориивременнóй стоимости денег. Теория временнóй стоимости денег – концепция, основанная на том, что деньги должны приносить процент; ценность денег, имеющихся в данный момент, выше, чем ценность той же суммы, которая будет получена в будущем.
Соответственно, неотъемлемой составляющей финансового анализа является учет фактора времени. В практических финансовых операциях суммы денег вне зависимости от их назначения или происхождения обязательно связываются с конкретными моментами или периодами времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность выплат. Вне времени нет денег. Фактор времени, особенно в долгосрочных операциях, играет не меньшую, а иногда даже и большую роль, чем размеры денежных сумм. Необходимость учета временного фактора вытекает из сущности финансирования, кредитования и инвестирования и выражается в принципе неравноценности денег, относящихся к разным моментам времени, т.е. «время – деньги».
Одинаковые суммы денег «сегодня» и «потом» оцениваются по-разному. Сегодняшние деньги приравниваются к возросшей денежной массе в будущем и, наоборот, вместо денег «потом» можно согласиться на уменьшенные выплаты, но сейчас.
Неравноценность двух одинаковых по абсолютной величине разновременных сумм определяется следующим:
во-первых, имеющиеся сегодня деньги могут быть инвестированы и принести доход в будущем (полученный доход в свою очередь реинвестируется и т.д.), т.е. возможностью использования денег как приносящего доход финансового актива;
во-вторых, - неопределенностью будущего и связанным с нею риском. Деньги «в кармане» могут быть израсходованы на потребление сиюминутно. Сберегаемые же деньги подвержены всевозможным рискам в зависимости от способа сбережения. Если они хранятся на «домашнем депозите», им грозит обесценение из-за инфляции или потеря в результате ограбления, пожара и т.д.
В случае, когда деньги даются в долг, риск невозврата зависит от успешности кредитуемого мероприятия, которое может завершиться убытками и полным крахом. Поэтому возвращаемая сумма всегда должна быть больше заемной как с учетом срока ссуды, так и существующего риска потерь.
Очевидным следствием временной стоимости денег является неправомерность суммирования денежных величин, относящихся к разным моментам времени, особенно при принятии решений финансового порядка. Их сравнение допустимо только при «приведении» таких сумм к одному моменту времени. Формулы, которые будут рассмотрены ниже, позволяют пересчитывать и приводить денежные потоки к различным временным датам без учета фактора неопределенности.
Наращение
Наращение – приведение денежных потоков (денежных сумм) к одному моменту времени в будущем.
Рассмотрим формулы расчета будущих суммSпо начальному вкладуР. В основе их построения лежит понятие единичного периода начисления(n=1) и процентной ставкиi, которая фиксирует процентное увеличение исходной суммы Р за первый период. В результате сумма на конец этого периода времени составляет:
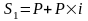 ,
,
где процентная ставка i измеряется десятичной дробью.
По отношении к следующим периодам начисления ставки процентов трактуются по-разному в зависимости от принятой схемы начисления: по простым или по сложным процентам. В первом случае приросты денежных сумм для любого периода будут составлять все ту же долю i от первоначальной суммы Р. В результате наращенная за n периодов сумма составит величину
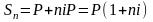 ,
(1)
,
(1)
где n – срок в годах.
В отличие от простых для сложных процентов одна и та же ставка i берется для каждого последующего промежутка не от первоначальной суммы, а от результата предыдущего начисления, т.е. от суммы, наращенной на начало данного периода. Отсюда следует, что вклад Р при ставке сложного процента i через n периодов составит сумму
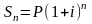 (2)
(2)
Множители
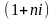 и
и
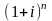 - множители наращения соответственно
по простым и сложным процентам.
- множители наращения соответственно
по простым и сложным процентам.
Т.о. последовательность
наращенных сумм
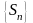 в случае простых процентов представляет
арифметическую прогрессию, в то время
как для сложных процентов прогрессия
будет геометрической.
в случае простых процентов представляет
арифметическую прогрессию, в то время
как для сложных процентов прогрессия
будет геометрической.
Выражения (1), (2) называют формулой простых и, соответственно, сложных процентов, а под процентными деньгами или, кратко, процентами понимают величину дохода (приращения денег)
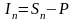
В финансовых вычислениях в случае меняющихся во времени процентных ставок используют следующие формулы
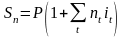 - для простых
процентов,
- для простых
процентов,
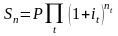 - для сложных
процентов.
- для сложных
процентов.
Дисконтирование
Дисконтирование – приведение всех денежных потоков (денежных сумм) к одному моменту времени в прошлом.
Эта процедура в определенном смысле является обратной по отношению к процессу наращения.
Другим вариантом дисконтирования является учет векселей в банке, когда банк, принимая вексель от предъявителя, выдает ему обозначенную на векселе сумму до срока его погашения. При этом банк удерживает в свою пользу проценты (дисконт) от суммы векселя за время, оставшееся до срока его погашения. Подобным образом (с дисконтом) государство продает большинство своих ценных бумаг (долговых обязательств).
При дисконтировании исходной величиной выступает не начальный вклад Р, а некоторая будущая сумма S. Вопрос состоит в том, чтобы определить эквивалентную сумму Р, отстоящую на n периодов до срока выплаты S.
Существует два подхода к расчету предшествующих сумм.
Во-первых, по размеру вклада Р, который при начислении процентов через n периодов дает сумму S, и,
во-вторых, по размеру платежа, к которому придем при удержании процентов с финальной суммы S за n периодов.
Т.о. при одном толковании за базовую величину, т.е. за 100%, принимается размер вклада Р, в то время как при другом – за 100% берется будущая сумма S. Кроме того, по каждому варианту дисконтирование может проводиться как по простым, так и по сложным процентам.
В случае приведения по вкладу Р для нахождения дисконтированных значений достаточно воспользоваться формулами простых и сложных процентов (1) и (2), решив их относительно величины Р.
В результате получим формулы
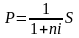 (3)
(3)
дисконтирования по простым процентам и
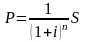 (4)
(4)
дисконтирования по сложным процентам.
Множители
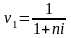 и
и
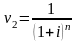 называются дисконтными
множителямипо процентной ставке
и показывают, какую долю составляет Р
в величине S
при простой и при сложной процентной
ставке.
называются дисконтными
множителямипо процентной ставке
и показывают, какую долю составляет Р
в величине S
при простой и при сложной процентной
ставке.
Величину Р, найденную дисконтированием S по вкладу, называют современной, или приведенной величинойS. Это понятие является одним из важнейших в количественном анализе финансовых операций, поскольку именно с помощью дисконтирования учитывается фактор времени.
Дисконтирование по платежу.
За основу их построения можно принять понятие единичного периода удержания процентов (дисконтирования) и учетной ставкиd, которая фиксирует процентное или долевое уменьшение суммы S на один период «назад». Отсюда следует, что за один период удержания эквивалентная выплате S сумма составит величину Р, которая при дробном измерении ставки d определяется формулой
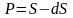 .
.
По отношению к следующим периодам учетная ставка трактуется по-разному в зависимости от принятой схемы дисконтирования: по простым или по сложным процентам. В первом случае удержания денежных сумм (дисконты) по каждому периоду будут составлять все тот же процент dотвсе той же суммы S. В результате такого дисконтирования за n периодов получится величина
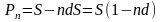 (5)
(5)
В отличие от этого при учете по сложной ставке последовательные по периодам снижения берутся как один и тот же процент d, но не от одной и той же величины S, а каждый раз от новой, полученной в результате дисконтирования на соседний период. Отсюда следует формула дисконтирования (учета) по сложным процентам, где в качестве процента выступает доля удержания d
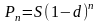 (6)
(6)
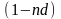 и
и
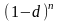 - дисконтные множители соответственно
по простой и сложной учетной ставке.
- дисконтные множители соответственно
по простой и сложной учетной ставке.
Схема дисконтирования по процентной ставке (3), (4) широко применяется для сравнения потоков платежей и при расчете стоимости облигаций и других ценных бумаг.
Дисконтирование по учетной ставке (5), (6) используется при учете векселей.
Суть данной финансовой операции состоит в следующем. Некто выдает вексель (расписку) с обязательством уплатить сумму S на определенную дату Т. Владелец векселя в случае нужды может досрочно учесть его, т.е. получить деньги раньше срока в коммерческом банке по установленной последним учетной ставке d, которая уменьшает сумму выплаты. В зависимости от принятых условий учет проводится по простым (5) или по сложным (6) процентам.
Такой вексель, который допускает участие третьих лиц, называется переводным или траттой. В дальнейшем, на дату Т, банк предъявляет вексель тому, кто его выписал, и получает сумму S.
Отметим, что такой известный инструмент кредитно-денежной политики, как учетная ставка Центрального Банка, используется им по большей части не только для переучета векселей коммерческих банков, сколько для взыскания с них платежей по коммерческим кредитам. Подобная практика использования учетной ставки, существующая во многих странах, сложилась исторически.
Учетная ставка – ставка процента, под который ЦБ страны предоставляет кредиты коммерческим банкам. В практике РФ применяется термин «ставка рефинансирования».
Учетная ставка – учетный процент, взимаемый банком с суммы векселя при покупке его банком до наступления срока платежа.
