1.3.4. Волна Стонели-Шолте на границе

раздела твёрдого тела и жидкости.

,

,

.

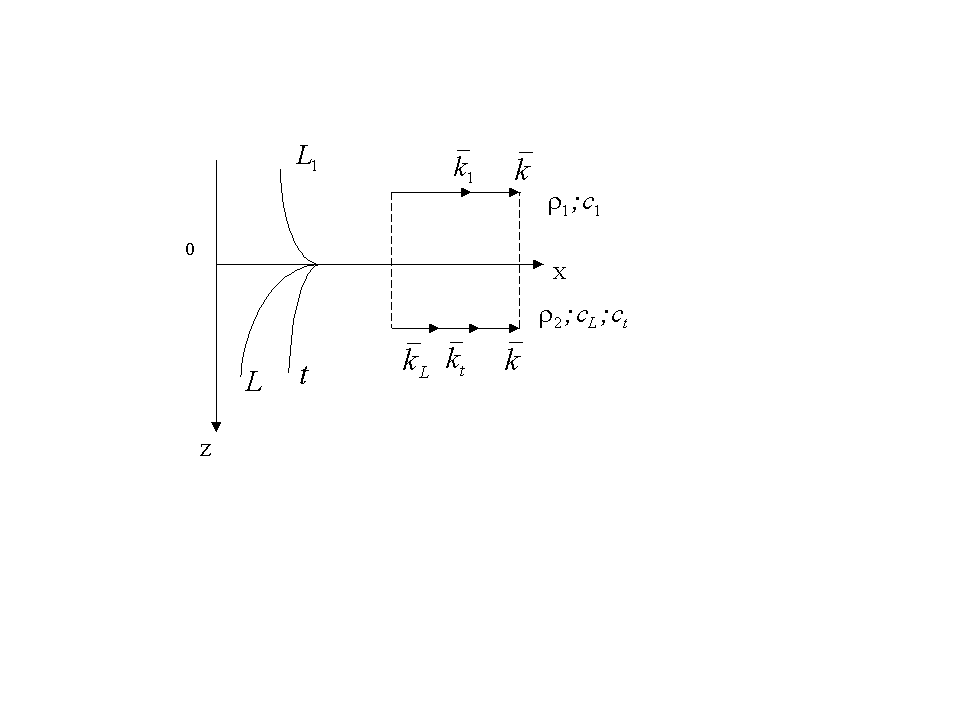
Граничная задача в рассматриваемом случае записывается в следующем виде:

. (1.35.)

Решение задачи (1.35.) будем искать в виде волны, локализованной в пограничном слое, амплитуда которой экспоненциально убывает при удалении от границы.

. (1.36.)

Подстановка решения в граничные условия даёт нам систему трёх уравнений относительно трёх произвольных постоянных :

.

Произвольные постоянные определяются с точностью до отношения:

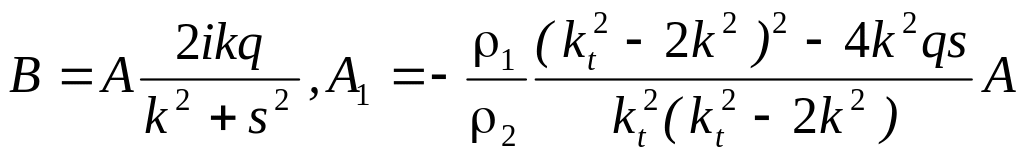, а равенство нулю определителя даёт характеристическое уравнение для определения скорости волны Стоннели-Шолте :

. (1.37.)

Структура волны может быть представлена набором следующих единичных векторов:

,

,

,

где: - единичные векторы с нормированной (единичной) амплитудой горизонтальной составляющей. Используя соотношения между произвольными постоянными , запишем структурную формулу для векторов в виде:

,

,

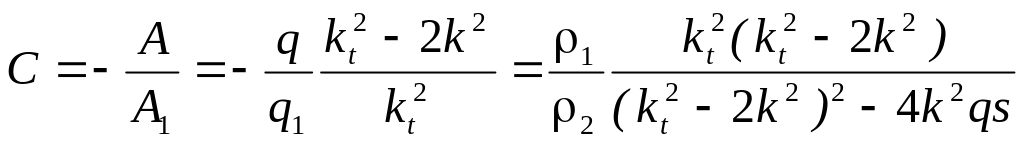Другой подход и вывод уравнения (1.37.) связан с понятием входного импеданса. Так, например, решение в верхнем полупространстве можно определить, подчинив его импедансному граничному условию на границе :

,

. (1.38.)

Подставляя в (1.38.) , получаем:

или в другом виде:

. (1.39.)

Уравнение в форме (1.39.) поясняет процесс формирования поверхностной волны Стонели-Шолте. Эта волна, распространяясь со скоростью , которая меньше наименьшей из всех скоростей в сопряжённых средах , характеризуется такой степенью неоднородности, при которой реактивный импеданс упругого характера полностью компенсирует суммарный реактивный импеданс инерционного характера .

Это означает, что волна Стонели-Шолте, также как и волна Релея, относится к поверхностным волнам резонансного типа.

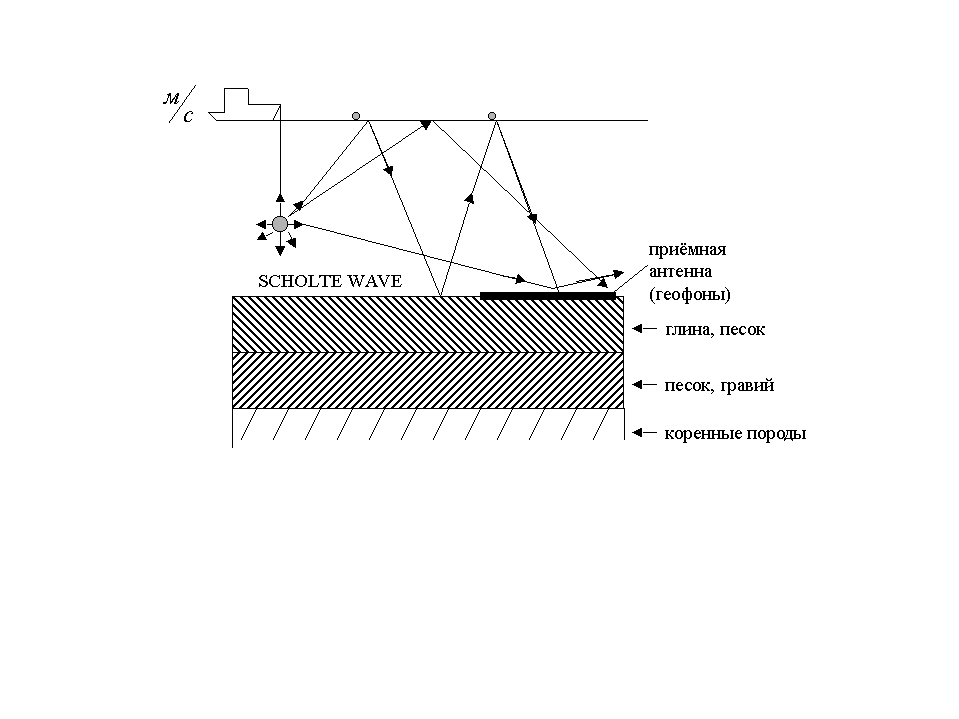
Волны Стонели-Шолте нашли очень интересное применение в морской геологии для определения параметров морских осадочных пород. Эти породы, обладая малой сдвиговой упругостью, оказывают сильное влияние на распространение звуковых волн в морской среде, существенно увеличивая потери на распространение.

Волна Стонели-Шолте хорошо обнаруживается в экспериментах по распространению широкополосных сигналов от взрывных источников вблизи дна как низкоскоростная волна, скорость которой незначительно меньше скорости поперечных волн в морских осадках.

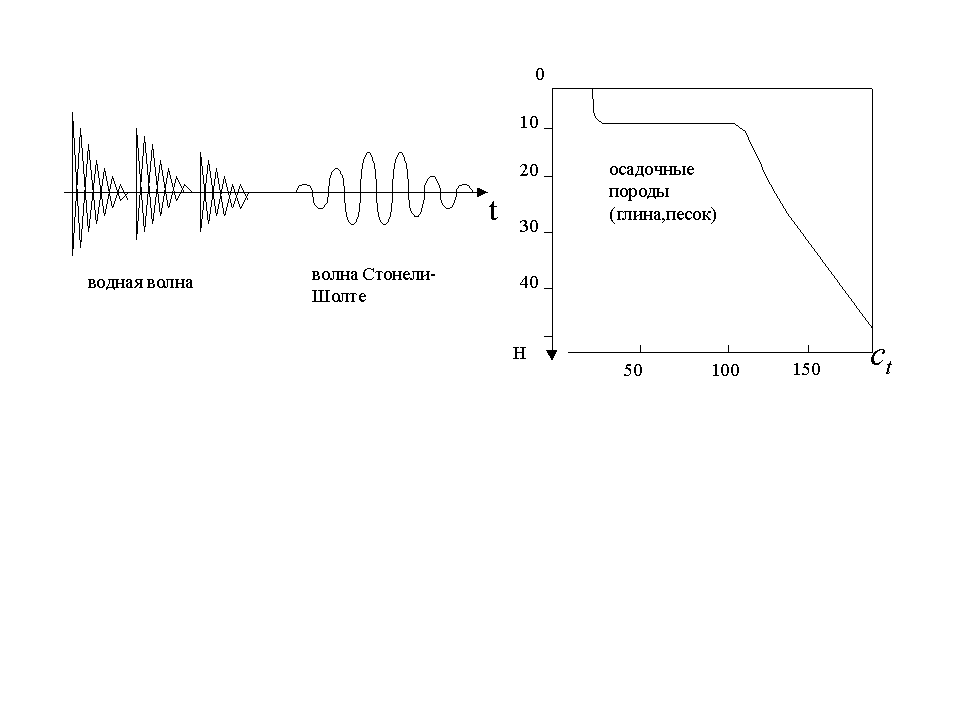
В верхних слоях осадков скорость увеличивается с глубиной до значений затухание волны Стонели-Шолте растёт с ростом частоты, поэтому в эксперименте фиксируются только низкочастотные составляющие (~ герц), а в качестве источника используют взрывные источники звука. Примерные характеристики осадочных пород и коренных пород (базальт) даны в таблице:

вода	1540	------	0,0	------	1,0
осадки	1535	180	0,1	1,5	1,3
базальт	3000	1100	0,3	0,5	2,3

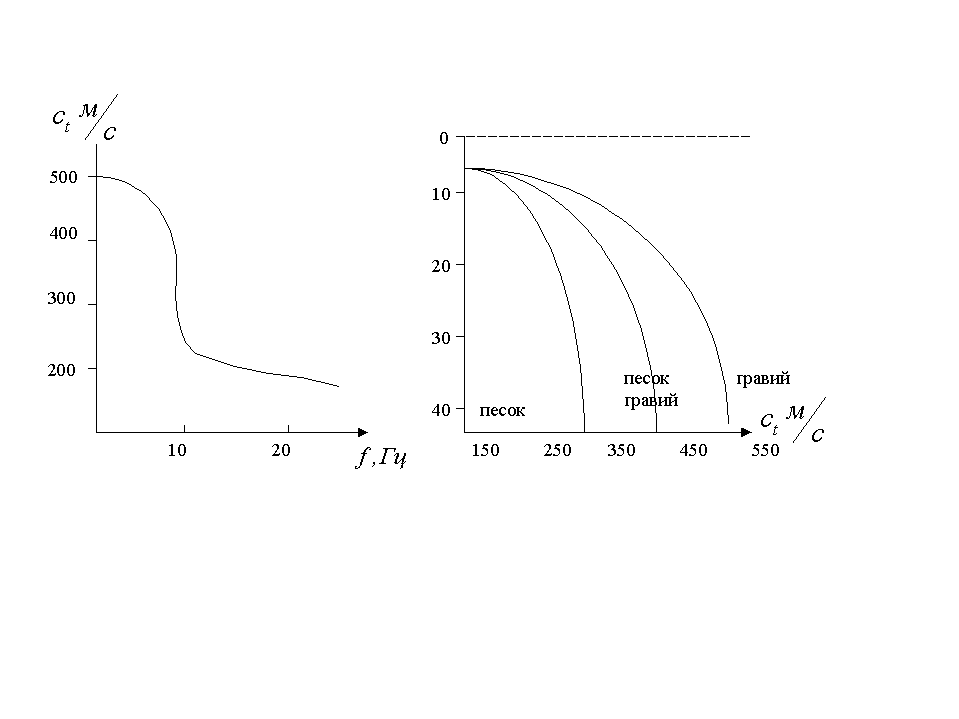
В дальнейших работах по регистрации волны Стонели-Шолте с использованием методов спектрального анализа была измерена групповая скорость отдельных спектральных составляющих и построена дисперсионная зависимость для волн Стонели-Шолте.

В свою очередь, дисперсионная зависимость объясняется изменчивостью скорости с глубиной в слое морских осадков, поэтому по дисперсионной зависимости можно оценить профиль изменения с глубиной залегания осадочных пород.

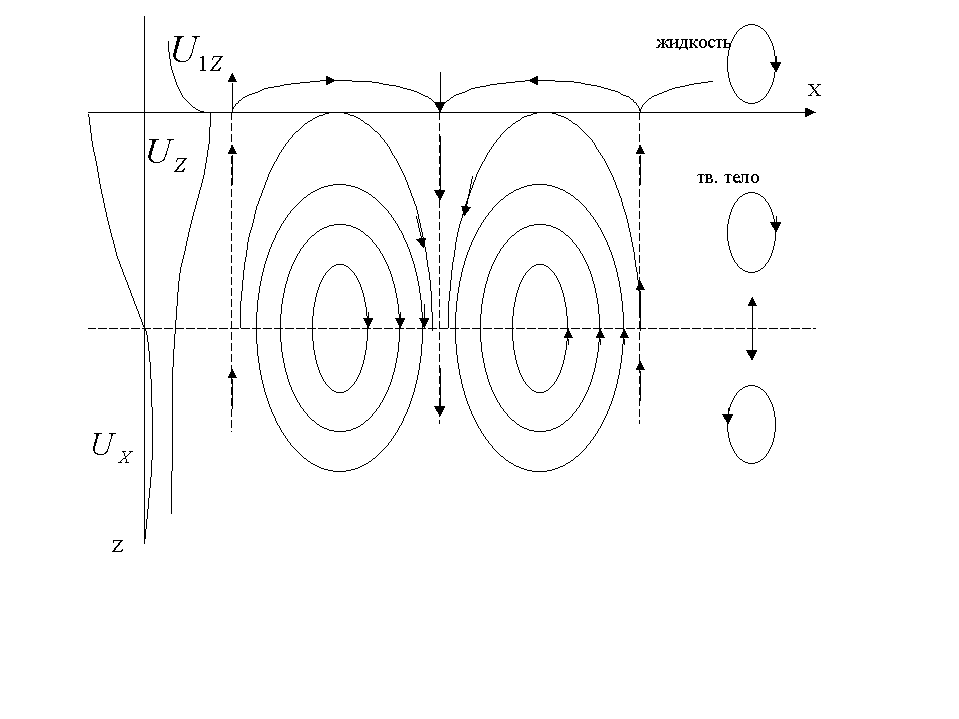
Волна Стонели-Шолте в обоих средах является неоднородной волной, а компоненты сдвинуты по фазе на как в жидкости, так и в твёрдом теле. Структура векторных линий поясняется рисунком: