1.3.2. Поверхностная волна Релея.

Рассмотрим более подробно структуру волны Релея, получив основные соотношения из решения граничной задачи (1.24.) в отсутствие падающей волны:

, ,

.

Решение граничной задачи имеет вид:

.

Напряжения через потенциалы выражаются следующим образом:

,

.

Подставляя решение (1.28.) в граничные условия получаем следующую однородную систему:

.

Из её решения определяется соотношение между произвольными постоянными, т.е. структура волн Релея, а из условия равенства нулю определителя (уравнение Релея) определяется скорость волны Релея:

,

. (1.29.)

Структура волны Релея даётся формулами:

,

.

или в векторной форме:

,

.

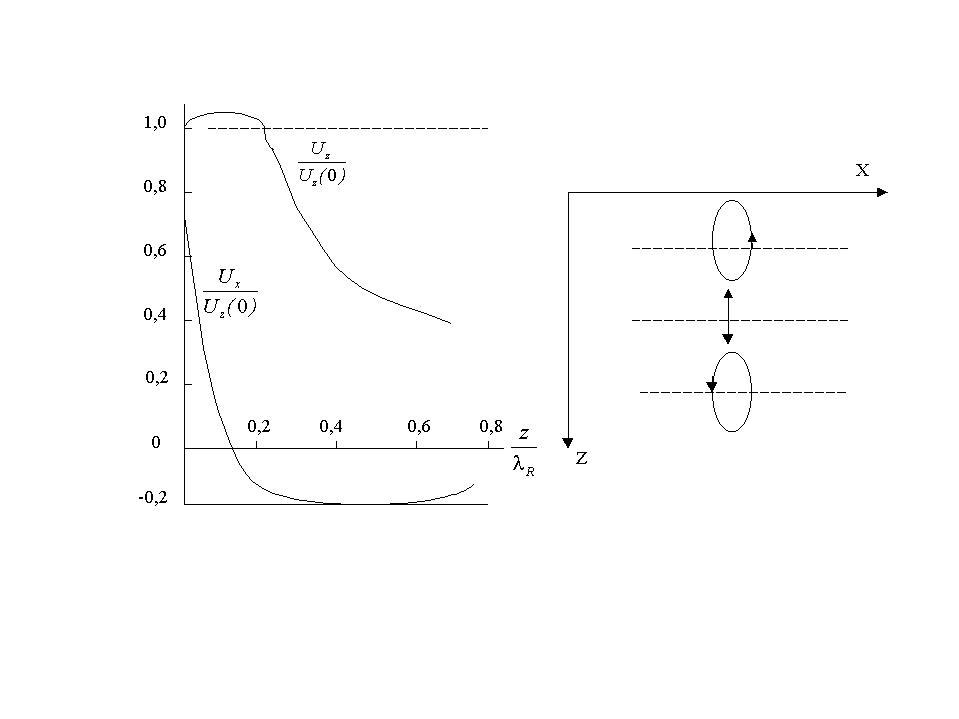
Компоненты смещены по фазе на , что говорит о том, что частицы среды движутся в поле волны Релея по эллипсоидальным траекториям.

Можно показать, что входной импеданс твёрдого тела, определённый на поверхности, свободной от сдвиговых напряжений, имеет вид:

.

Для неоднородной продольной волны, амплитуда которой экспоненциально убывает при удалении от поверхности, составляющая

имеет реактивный инерционный характер, тогда как для неоднородной поперечной волны составляющая имеет реактивный упругий характер.

Уравнение Релея выражает условие равенства нулю входного импеданса твёрдого тела: , (1.32.)

т.е. волна Релея есть поверхностная волна резонансного типа, скорость которой отвечает условию полной компенсации инерционной и упругой составляющих полного сопротивления, для чего скорость должна быть меньше продольной и поперечной скоростей, а волна должна экспоненциально затухать при удалении от поверхности – такая волна называется неоднородной. Локализацией волны у поверхности объясняется и более слабый, цилиндрический закон ослабления её амплитуды с расстоянием: .

Вертикальная и горизонтальная компоненты вектора смещения сдвинуты по фазе на , а частицы среды движутся по эллипсоидальным траекториям.

Структура векторных линий тока поясняется рисунком.

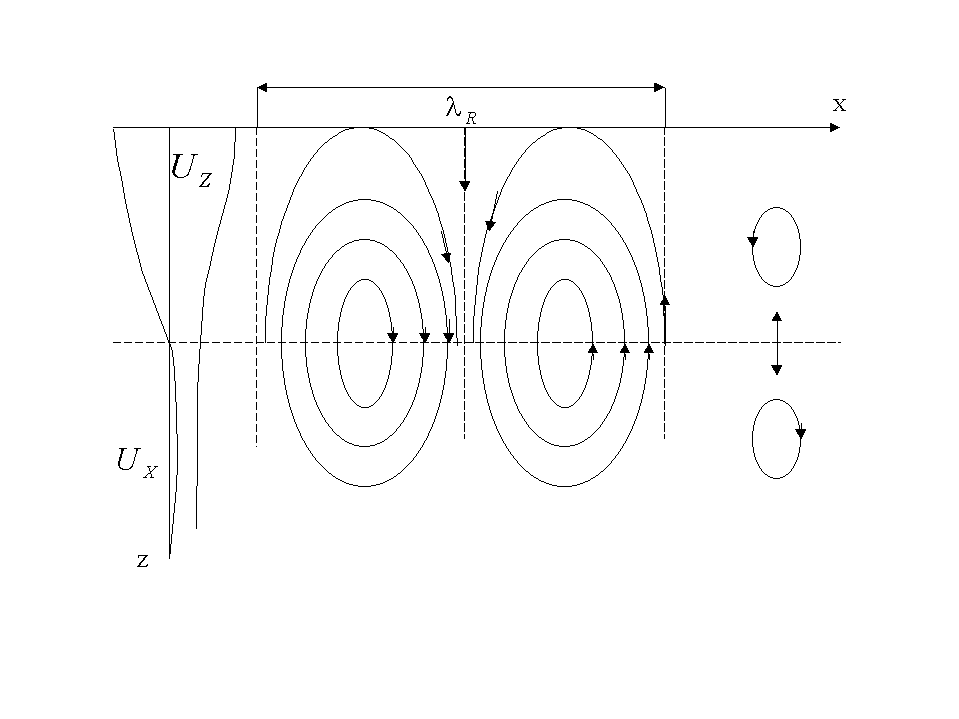
1.3.3. Волновое движение на границе раздела двух жидких сред.

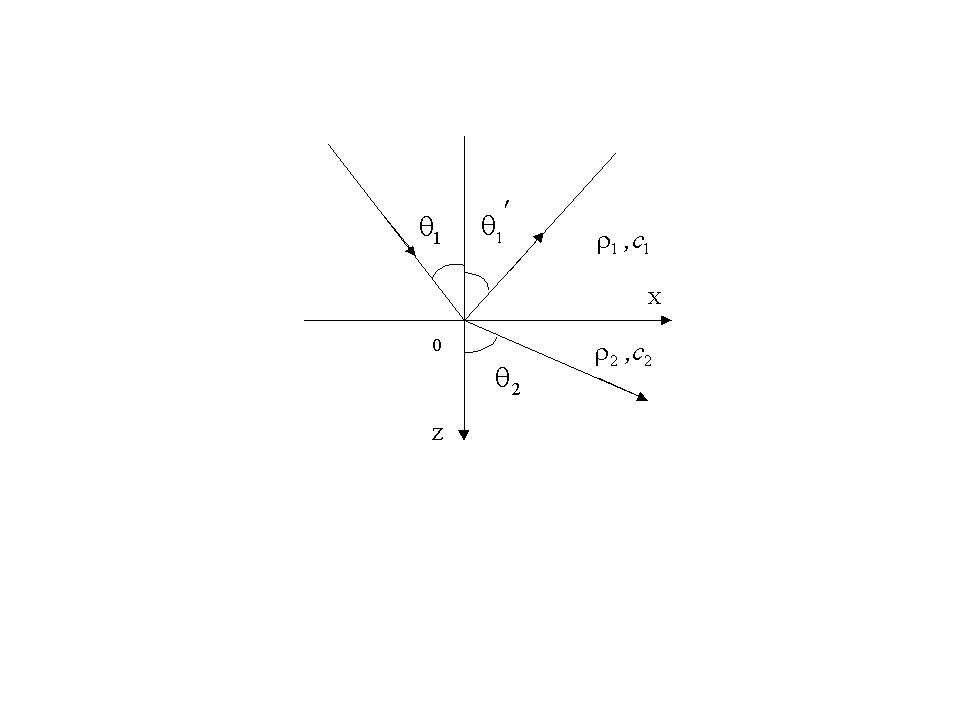
Задача на отражение плоской волны на границе раздела двух жидких сред записывается в виде:

,

. (1.33.)

Для решения задачи (1.33.) вводят отражённую и прошедшую волны, амплитуды которых определяются граничными условиями (1.33.).

,

,

,

.

Нормальные к границе раздела потоки мощности удовлетворяют закону сохранению энергии в форме:

, .

- коэффициенты отражения и прозрачности по вертикальной компоненте потока мощности.

Горизонтальные компоненты потока мощности не являются непрерывными, причём горизонтальный поток мощности в верхней среде не является однородным по координате . Скорость переноса энергии в верхней среде будет зависеть от координаты в силу интерференционной структуры самого поля. Определяя в верхней среде через усреднённые по величины можно получить соотношение:

.

Для нижней среды при вещественных углах преломления:

.

В случае имеет место полное внутреннее отражение при критическом угле :

, а при поле в нижней среде становится неоднородным по координате :

.

В неоднородной звуковой волне групповая скорость должна определятся только через энергетические характеристики:

, причём .

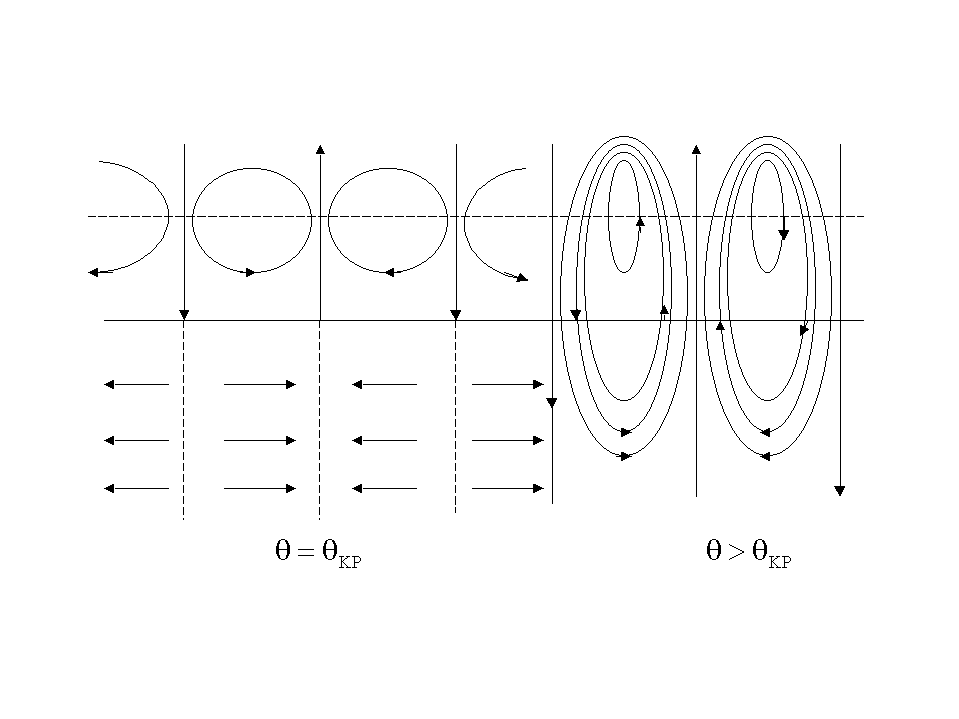
Общий характер изменения фазовой и групповой скоростей в соответствующих средах поясняется рисунком:

Структура звукового поля в нижнем полупространстве при углах имеет характерные особенности – компоненты вектора колебательной скорости сдвинуты по фазе на , и убывают при удалении от границы раздела, что характерно для реактивного поля.

Входной импеданс нижнего полупространства является чисто реактивным, инерционным:

, а векторные линии тока образуют замкнутую систему линий.

В рассматриваемом случае границы раздела двух жидких сред не существует какой либо пограничной волны, локализованной вблизи границы раздела. Это объясняется тем, что входной импеданс двух неоднородных волн, локализованных с каждой стороны границы, является реактивным, инерционным, и ни при какой их комбинации не обращается в нуль.

Однако, возможно существование обобщённой поверхностной волны, которая формально является решением следующей однородной граничной задачи:

, ,

, , ,

где: - входной импеданс нижнего полупространства, - постоянная распространения, соответствующая решению типа плоской волны, распространяющейся вдоль границы раздела с фазовой скоростью .

Общее решение задачи имеет вид:

,

,

а структура волны определяется однородной системой уравнений:

, и характеристическим уравнением, которое можно записать в виде:

,

где: - входной импеданс верхнего полупространства. (1.34.)

Характеристическое уравнение (1.34.) имеет решение:

.

Построенное решение есть неоднородная волна, амплитуда которой экспоненциально убывает при удалении от границы раздела в верхнем полупространстве и экспоненциально растёт в нижнем полупространстве. При такой конструкции неоднородной волны входной импеданс верхнего полупространства – реактивный, инерционный, а входной импеданс нижнего полупространства – реактивный, упругий:

.

Сама волна является волной резонансного типа, для которой суммарный входной импеданс двух полупространств равен нулю.

При непрерывном продолжении поля из верхнего полупространства в нижнее мы получим решение, неограниченно растущее в нижнем полупространстве. Поскольку физический смысл имеют только ограниченные решения, мы должны предположить, что амплитуда волны в нижнем полупространстве принимает конечное значение в окрестности бесконечно удалённой точки, а само решение можно построить предельным переходом вида:

,

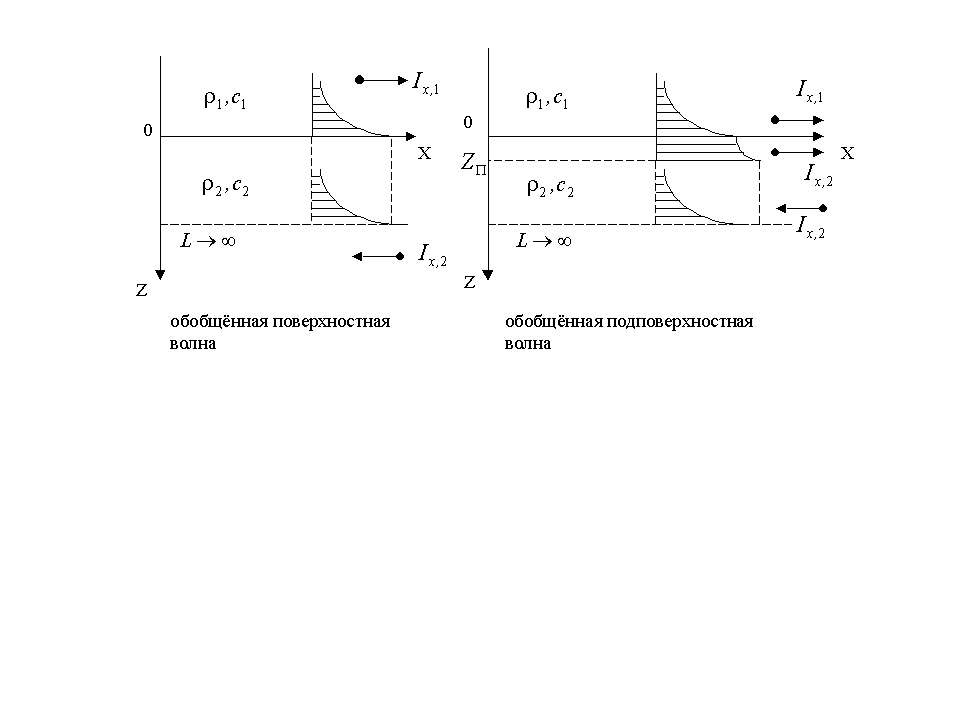
Построенное решение описывается обобщёнными функциями, разрывными либо на границе раздела , либо на некотором подповерхностном горизонте . Соответствующие волны являются обобщённой поверхностной волной или обобщённой подповерхностной волной соответственно.

При рассмотрении обобщённых поверхностных волн, возникающих в конкретных задачах, соответствующих реальным источникам возбуждения, оказалось, что потоки мощности в полупространстве, где расположен источник, и в окрестности бесконечно удалённой точки нижнего полупространства, где решение представлено обобщённой волной, имеют противоположные направления. Это означает, что мощность, приходящаяся на данный тип волнового движения и определяемая разностью потоков мощности, минимальна, а коэффициент возбуждения обобщённой поверхностной волны максимален (в сравнении с другими волнами в сходных условиях возбуждения).