1.2.8. Энергия звукового поля.

Звуковое поле обладает энергией: кинетическая энергия связана с движением среды, а потенциальная энергия с её деформацией. Звуковая волна переносит энергию в направлении распространения. Для вывода энергетических соотношений рассмотрим уравнение движения в скалярном случае:

Умножим его скалярно на вектор :

и выполним преобразование:

,

.

Интегрируя последнее равенство по произвольному объёму, получаем математическое выражение закона сохранения энергии:

, (1.22.)

- плотность кинетической и потенциальной энергии соответственно.

- вектор Умова-Пойнтинга (вектор потока энергии).

При гармонической зависимости от времени все величины можно усреднить за период рабочей частоты:

,

,

- амплитудные значения соответствующих величин, - интенсивность звука.

Для звуковой волны, распространяющейся в твёрдом теле, закон сохранения энергии в форме (1.22.) также имеет место при соответствующем переопределении величин:

,

- колебательная скорость.

Групповая скорость через введенные энергетические величины может быть определена отношением , и означает скорость переноса энергии в направлении распространении волны.

1.3. Особенности волнового движения при наличии границ раздела.

1.3.1. Отражение от свободной поверхности полупространства.

Волновое движение, формирующееся при наличии границ раздела, трактуют обычно как результат наложения падающей волны и возникающих при этом отражённой и преломлённой волн. Если последняя комбинация возможна при отсутствии падающей волны, то говорят о наличии собственной формы волнового движения или поверхностной (приповерхностной) волны. Примерами таких волн являются волны Релея и Стоунли (Стоунли-Шолте).

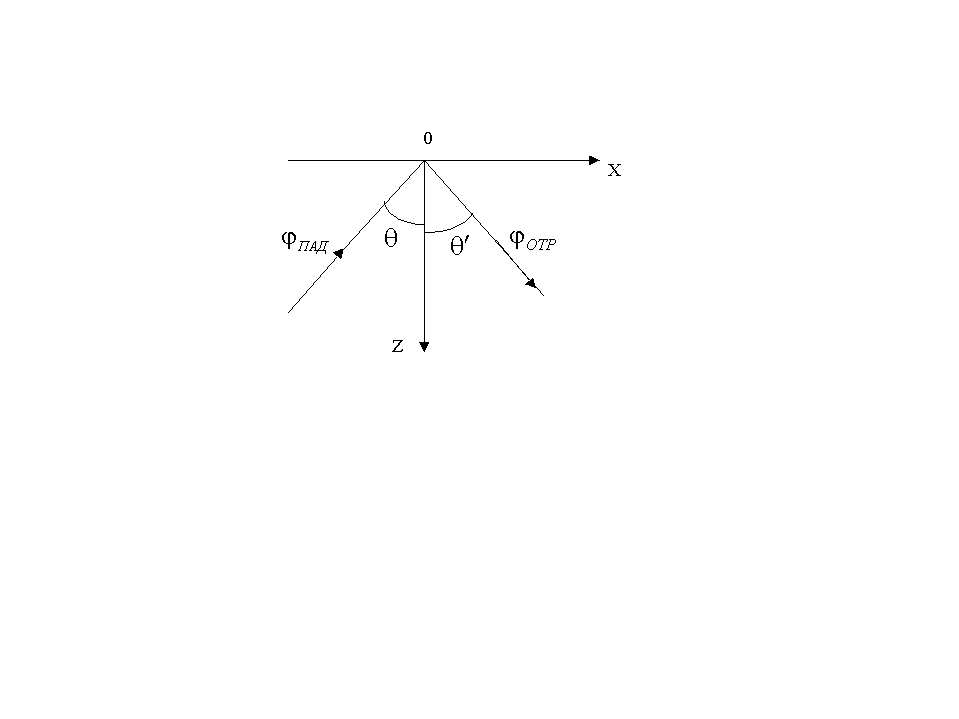
Рассмотрим для примера волновое движение на свободной границе жидкого полупространства:

, . (1.23.)

Для решения граничной задачи (1.23.) вводят отражённую волну, амплитуда которой определяется граничным условием:

.

Полное описание поля в полупространстве даётся формулами:

,

.

Суммарное поле имеет характер стоячей по оси волны и бегущей вдоль оси волны, причём скорость распространения волнового фронта вдоль оси даётся выражением:

.

Групповая скорость, как скорость переноса энергии вдоль оси может быть определена двояко:

,

Оба определения совпадут, если групповую скорость в энергетическом смысле определить через усреднённые по координате величины:

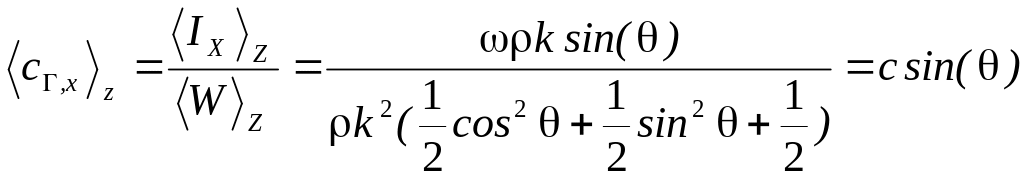
Из общих формул видно, что при суммарное поле стремится к нулю, что означает полную компенсацию падающей волны отражённой и невозможность существования собственных форм волновых движений (т.е. в отсутствие падающей волны) на свободной поверхности жидкого полупространства.

Из общих формул также видно, что горизонтальная и вертикальная компоненты вектора колебательной скорости сдвинуты по фазе на . Это означает, что частицы среды движутся по эллипсоидальным траекториям, а экстремумы компонент сдвинуты в пространстве на четверть пространственного периода.

На рисунке приведены эпюры распределения компонент колебательной скорости по оси и структура векторных линий тока в пространстве .

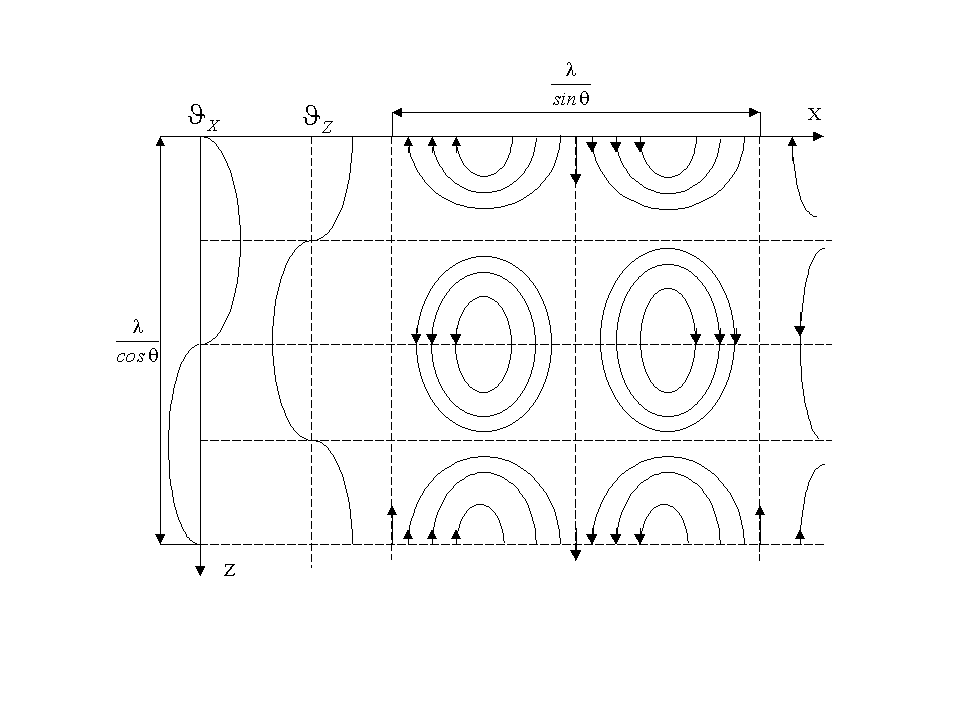
Такая поперечная структура звукового поля формируется всегда при наличии абсолютно отражающих границ, например, в волноводе. В результате вдоль оси устанавливается поле типа стоячей волны, в котором , а вдоль оси поле носит характер бегущей волны , с пространственным периодом .

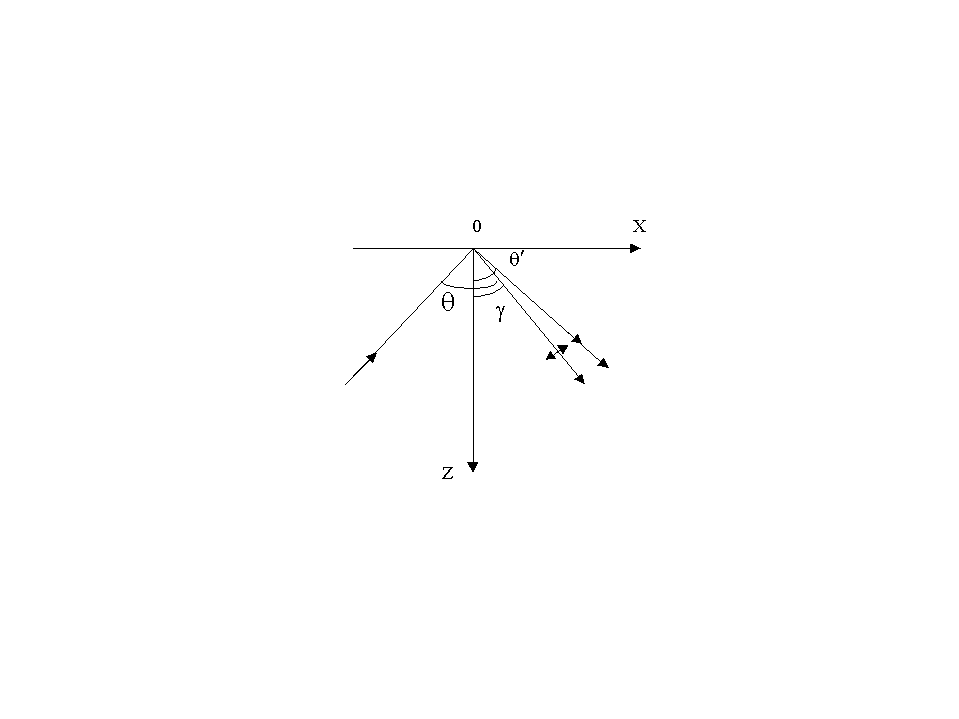
Рассмотрим теперь особенности отражения звуковой волны от свободной границы твёрдого тела.

,

. (1.24.)

Для решения граничной задачи (1.24.) нужно ввести отражённые продольную и поперечную волны, амплитуда которых определяется граничными условиями.

,

, - закон Снеля.

,

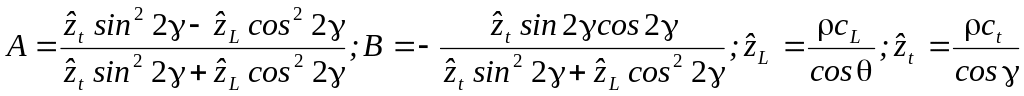Условие (1.25.)

определяет угол полной трансформации продольной волны в поперечную (и наоборот). Уравнение (1.25.) определяет два вещественных угла полной трансформации в области ( - коэффициент Пуассона).

Условие (1.26.)

Определяет существование на свободной поверхности твёрдого тела собственной формы волнового движения или волны Релея. Условие (1.26.) сводится к уравнению Релея:

(1.27.)

, - скорость волны Релея.

Два других корня уравнения (1.27.) являются корнями уравнения (1.25.) и определяют углы полной трансформации.

Структура корней поясняется рисунком:

сталь

Рассмотренный пример показывает, что при наличии границы раздела продольная и поперечная составляющие звуковой волны образуют связанную комбинацию, а их раздельное существование возможно только в некоторых частных случаях, например, в свободном пространстве.

В такой комбинации обе составляющие волнового движения распространяются с одной и той же скоростью вдоль оси :

, что и составляет содержание закона Снеля.

В отличие от фазовой, групповая скорость вдоль оси не определяется сколь нибудь простым соотношением через фазовую. Для её вычисления нужно воспользоваться энергетическим соотношением: , однако в суммарном поле: .

Для корректного определения групповой скорости нужно определить её через усреднённые по координате величины.

, (1.31.)

,

, причём в однородной плоской волне . Подставляя в (1.31.) решение граничной задачи, получаем следующее выражение:

, ,

.

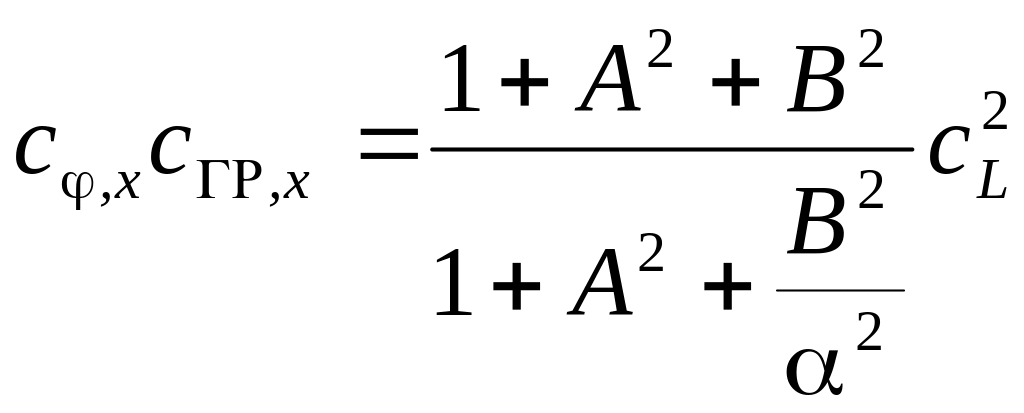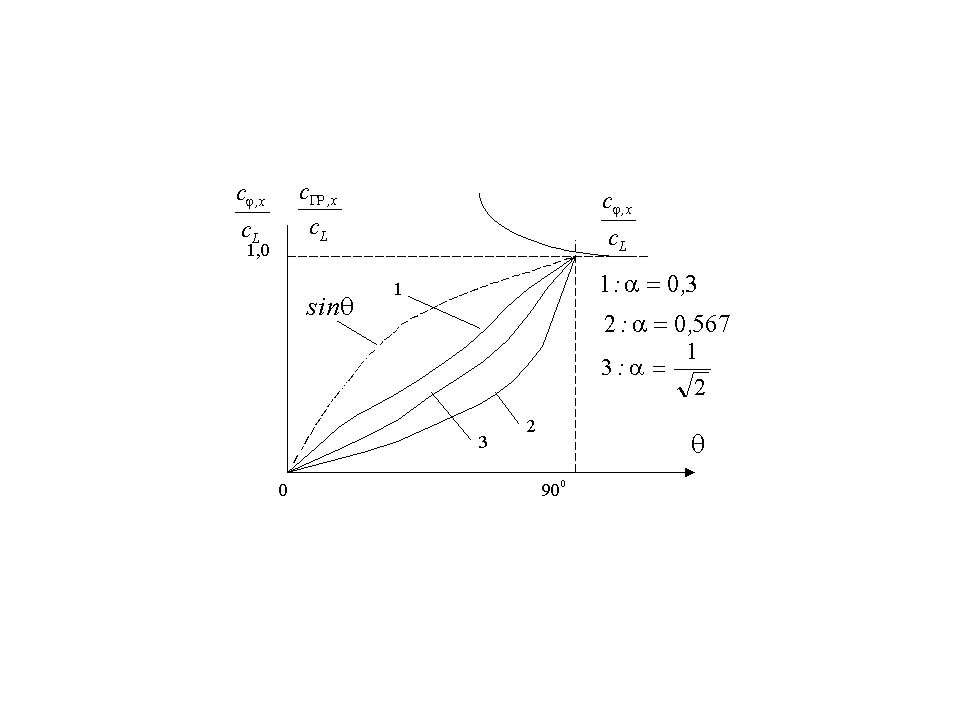
Эффект трансформации продольной волны в поперечную как бы замедляет скорость переноса энергии и уменьшает групповую скорость . Наибольшее уменьшение групповой скорости соответствует случаю .

При отражении поперечной волны от свободной поверхности эффект трансформации поперечной волны в продольную увеличивает скорость переноса энергии .

Эффект взаимной трансформации продольных и поперечных волн является характерной особенностью процесса распространения звуковой волны в твёрдом теле при наличии границ раздела.

Другая особенность связана со своеобразным проявлением сдвиговой упругости на свободной границе твёрдого тела, что проявляется в существовании поверхностной волны Релея.