1.1.3. Общие характеристики звуковых процессов.

К общим характеристикам произвольных звуковых процессов относят частотный и динамический диапазоны.

Частотный диапазон чрезвычайно широк и условно подразделяется на четыре поддиапазона:

- инфразвуковые колебания

Сюда относятся сейсмические колебания, связанные с движением (пульсациями) Земли как единого осциллятора с периодом - средняя скорость звука в Земле . , процессы, связанные с колебаниями гидросферы, которые порождают внутренние волны в океане и шельфовой зоне, модулирующие звуковые поля. Внутренние волны характеризуются частотой Брента-Вяйсяля:

- плотность, .

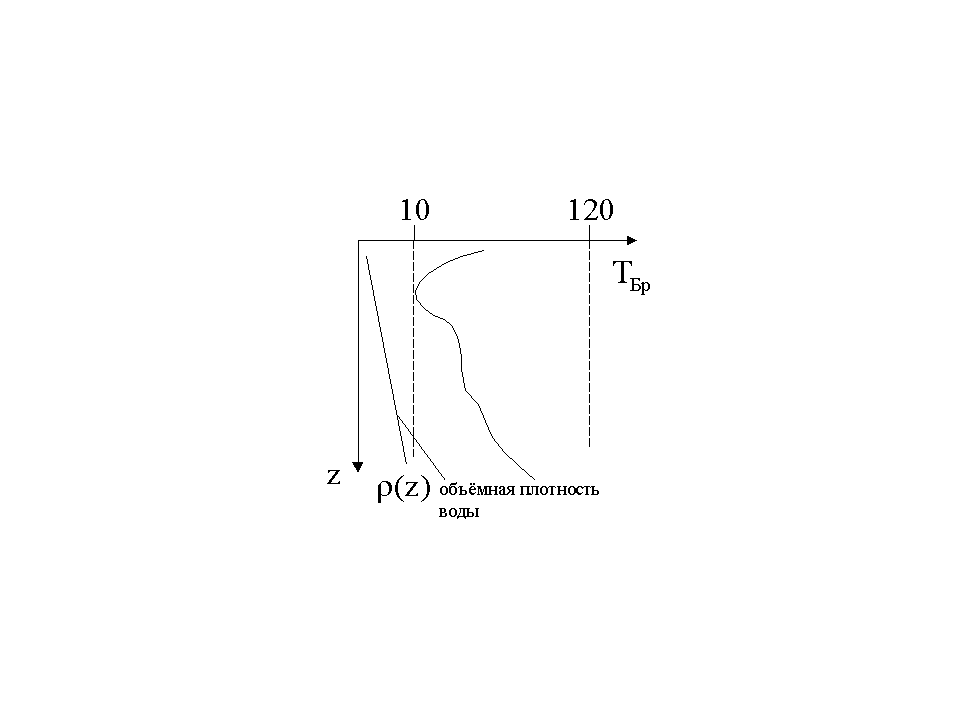
Частота Брента-Вяйсяля имеет характерное распределение по глубине моря. Периоды внутренних волн лежат в диапазоне , а также включают полусуточные и суточные периоды, связанные с поверхностным приливом.

Сюда же относятся колебания, связанные с вибрациями зданий и механизмов, шумовые процессы, строительные шумы, сейсмические шумы, шумы моря.

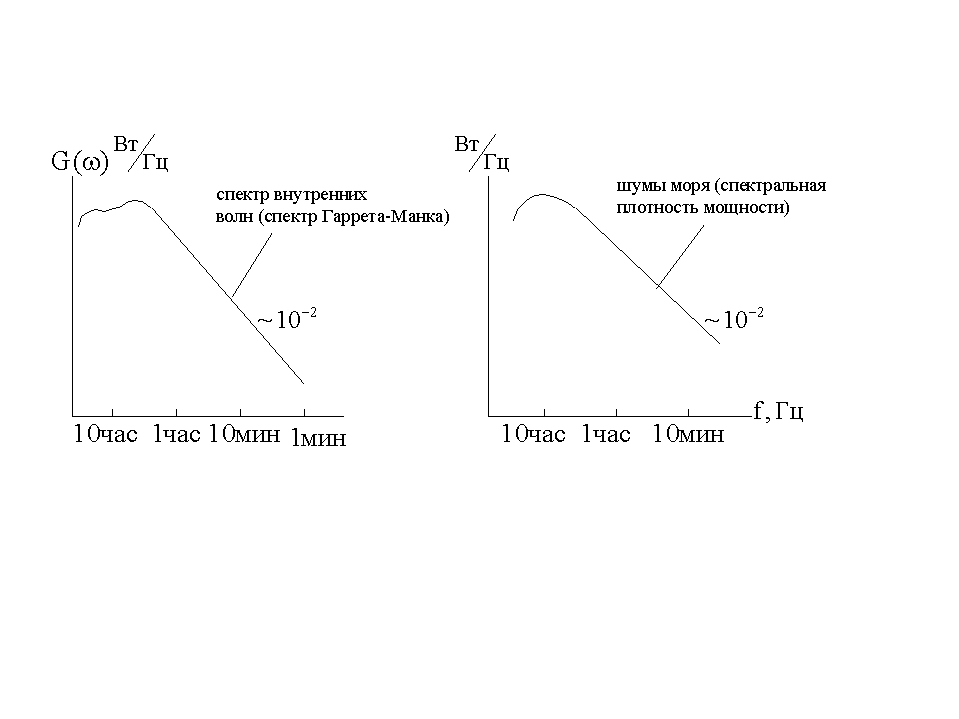
Шумовые процессы в море (шумы моря) и внутренние волны в океане характеризуются близкими по сути спектральными портретами.

Спектральная плотность мощности внутренних волн (спектр Баррета-Манка) и шумов моря имеют сходные частотные зависимости .

Гц. кГц. – звуковые колебания, т.е. колебания, воспринимаемые человеческим ухом: звуковая акустика (электроакустика), гидроакустика, биоакустика, мощный ультразвук и ультразвуковая обработка материалов, рыбопоисковая техника, акустические приборы сейсморазведки и сейсмопрофилирования, томография океана.

кГц. Гц. – ультразвук: ультразвуковая техника и ультразвуковая дефектоскопия, интроскопия и звуковидение , медицинская диагностика и ультразвуковая томография, верхний диапазон гидроакустики (гидролокаторы бокового и секторного обзора, доплеровские лаги, профилографы, измерители скорости течений).

Гц. – гиперзвук: физическая акустика, взаимодействие звука с веществом, молекулярная акустика, усиление гиперзвука в пьезополупроводниках, активные СВЧ-линии задержки.

Динамический диапазон также чрезвычайно широк, а для его сжатия применяют логарифмическую шкалу или уровень в децибеллах.

- логарифмический уровень в децибеллах.

Па – порог слышимости человеческого уха (0 дб).

Для воздушной среды при Па амплитуда колебательной скорости частиц среды , интенсивность звука .

20дб – тикание часов,

40дб – тихий разговор,

60дб – шум автомобиля,

80дб – громкий крик,

100дб – отбойный молоток (R~1м),

120дб – болевой порог уха (~20Па),

140дб – шум реактивного самолёта (R~100м),

180дб – шум реактивного самолёта (R~1м),

8090шум большого города (Нью-Йорк, Каир),

- шум в деловой части города,

200240дб – уровни мощных гидроакустических излучателей (взрывчатые источники и пневмопушки),

Па= . Общий диапазон: Па (260дб). В иностранной литературе в качестве уровня отсчёта используют Па (1 микропаскаль), .

1.2. Основные положения.

1.2.1. Основные уравнения акустики в жидких и газообразных средах.

Звуковое поле описывается следующим набором величин:

- звуковое (избыточное) давление,

- давление в невозмущённой среде,

- суммарное давление в возмущённой среде,

- вектор колебательной скорости,

- плотность среды.

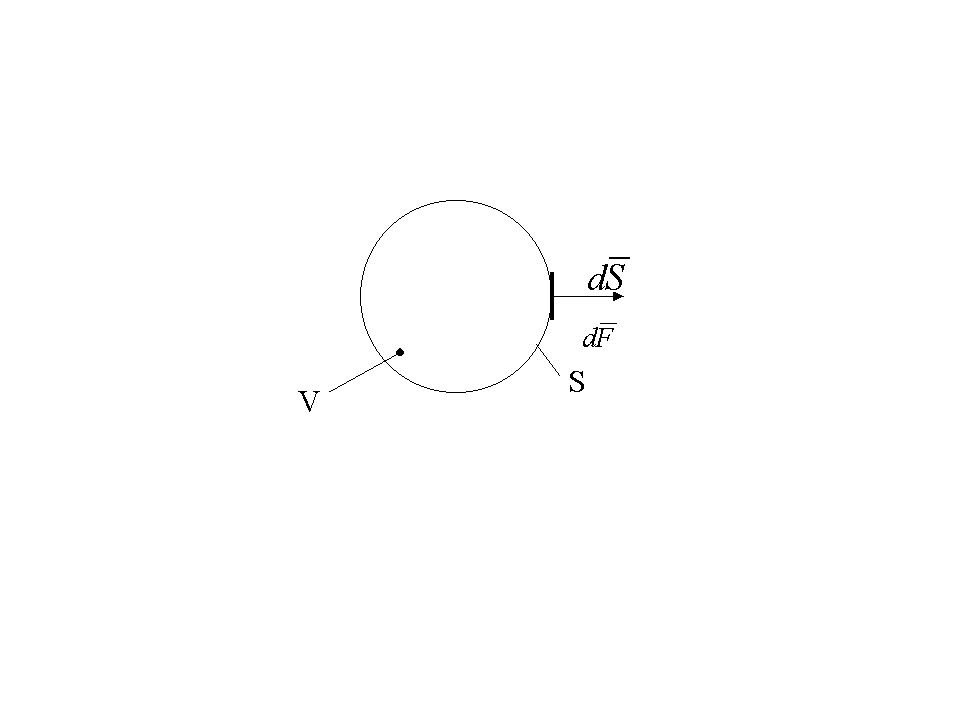
Уравнение движения записывается в виде уравнения баланса сил инерции и внешних сил, действующих через поверхность, ограничивающую произвольный объём, а в идеальной среде все силы, действующие через поверхность, являются нормальными:

- уравнение Эйлера (уравнение движения) (1.1.)

- постоянный вектор,

,

- оператор Набла,

- переносное ускорение,

- локальное ускорение.

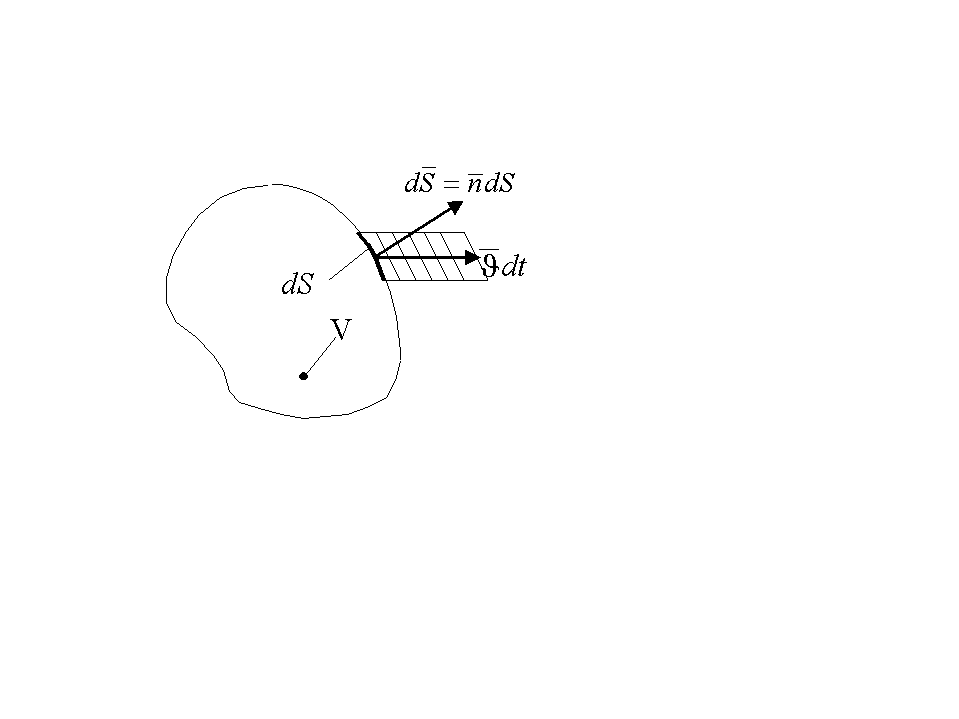
Уравнение неразрывности выводится из условия сохранения массы:

, ,

,

- уравнение неразрывности (1.2.)

В качестве третьего уравнения берут обычно уравнение состояния, связывающее давление и плотность. Считается, что процесс распространения звуковой волны является адиабатическим:

- уравнение адиабаты, - показатель адиабаты (1.3.)

для газов: - теплоёмкость при постоянном давлении или объёме. -для воздуха, - для воды.

- адиабатическая скорость звука в воздухе (1.4.)

Для жидких сред скорость звука вводят через адиабатическую сжимаемость:

В качестве других форм уравнения состояния используют разложение вида:

- скорость звука в невозмущённой среде.

;

- избыточное (звуковое) давление,

- давление в невозмущённой среде (атмосферное, гидростатическое).

Уравнения (1.1.), (1.3.) образуют замкнутую (полную) систему уравнений акустики относительно величин: , описывающих звуковое поле, все уравнения являются нелинейными.