1.1.2. Разделы акустики и их взаимосвязь.

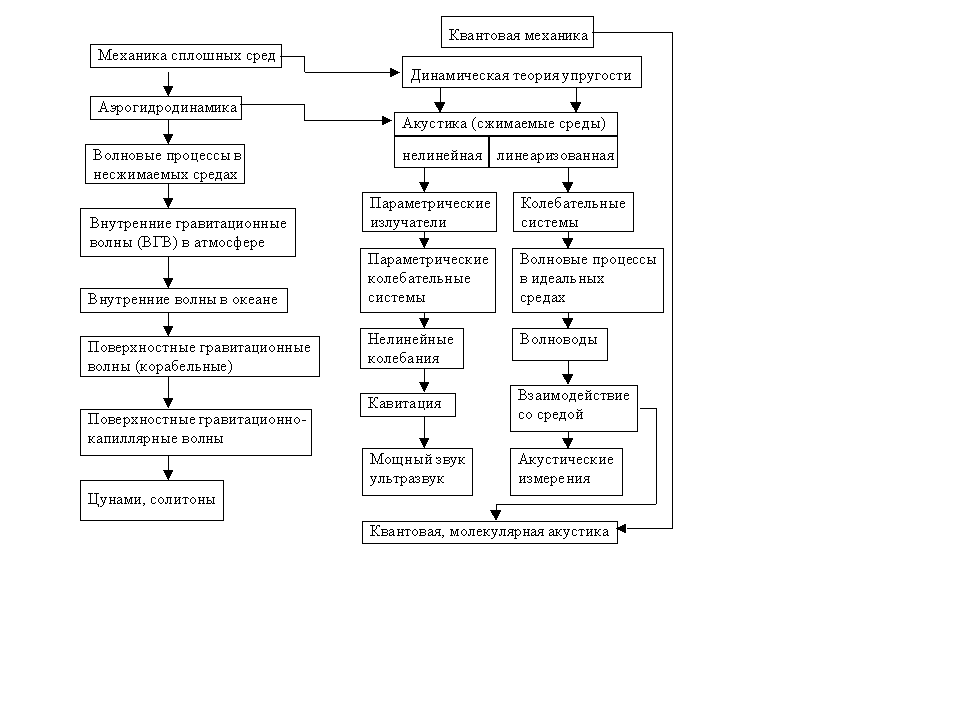
Какая-либо классификация современной акустики на отдельные разделы крайне затруднена большим разнообразием вопросов, лежащих в сфере её интересов, и взаимосвязью различных разделов либо на основе общности основных уравнений, либо на основе общности применяемых методов анализа.

Основу классической акустики составляют уравнения и понятия механики сплошных сред, которые обычно подразделяются на уравнения аэрогидродинамики, описывающие движение жидких и газообразных сред, и уравнения и понятия динамической теории упругости, описывающие движение в деформируемых твёрдых телах.

Основу квантовой и молекулярной акустики составляют уравнения и понятия квантовой механики, учитывающие дискретную природу вещества и специфические квантовые эффекты. Граничной между представлениями классической и квантовой акустики является частота Дебая (с – скорость звука в твёрдом теле, d – межатомное расстояние в кристаллической решётке).

Основные уравнения акустики являются нелинейными, что сильно затрудняет их применение в общем случае и оправдывает в свою очередь некоторые приближения. Так, например, если пренебречь сжимаемостью среды, т.е. акустическими эффектами, то мы получим более простые уравнения, описывающие целый ряд волновых явлений, происходящих либо в атмосфере (внутренние гравитационные волны), либо в океане (внутренние волны), либо на поверхности воды (поверхностные корабельные волны, гравитационно-капиллярные волны). Самыми яркими представителями нелинейных волновых процессов являются уединенные (одиночные) волны - солитоны, открытые Расселом в 1844г., хотя более страшные их представители – волны цунами были известны гораздо раньше.

Если в основных уравнениях акустики пренебречь всеми нелинейными членами, т.е. выполнить при определённых условиях так называемую линеаризацию, то мы получим классическую линейную акустику, в рамках которой рассматривается большая часть всех вопросов, представляющих как теоретический, так и практический интерес. Именно эти разделы акустики проработаны наиболее глубоко и всесторонне и составляют традиционную линейную акустику. В рамках линейной акустики можно выделить как самостоятельные разделы теорию колебаний (имеются в виду акустические колебательные системы) и теорию волновых процессов.

В теории колебаний рассматриваются системы с сосредоточенными параметрами с N-степенями свободы, предельным случаем которых являются системы с распределёнными параметрами (стержни, концентраторы, мембраны и пластины, цилиндры и произвольные оболочки). Модельные колебательные системы могут быть либо линейными (одномерными), либо плоскими, либо трёхмерными (объёмными).

Наиболее сложными в описании являются произвольные трёхмерные колебательные системы с распределёнными параметрами на основе электроупругих сред (пьезокерамических материалов). Каждая колебательная система характеризуется спектром собственных (резонансных) частот и набором соответствующих им собственных функций или мод колебаний.

Характерная особенность колебательного процесса – преобразование энергии из потенциальной в кинетическую и наоборот, а также диссипация энергии при наличии потерь. Волновые процессы имеют место в неограниченных средах, однородных, неоднородных либо анизотропных (например, в кристаллах). Каждая волна характеризуется геометрией волнового фронта (плоские, цилиндрические, сферические волны), скоростью распространения в направлении нормали к волновому фронту и законом ослабления амплитуды волны с расстоянием. В рамках волнового описания строится теория излучения акустических волн и теория дифракции, теория направленного излучения и приёма, изучаются законы отражения и преломления звуковых волн на простейших границах раздела, плоских, статистически шероховатых, либо содержащих малые периодические неровности, законы рефракции в неоднородных средах.

Характерная особенность волнового процесса – перенос энергии в направлении распространения волны с некоторой скоростью, называемой групповой скоростью, строго ограниченной сверху. В отличие от неё скорость распространения волнового фронта, называемая фазовой скоростью, может быть любой.

Теория волноводов является сравнительно молодым разделом акустики, который быстро набирает силу. Достаточно сказать, что эта теория имеет прочные позиции и в атмосферной акустике, и в гидроакустике, и в геологии, а также на стыке этих дисциплин (например, в морской геологии). Более простыми свойствами обладают модельные волноводы с идеальными границами, заполненные однородной идеальной средой, жидкой либо газообразной. Наиболее сложными свойствами обладают многослойные либо неоднородные волноводы с импедансными границами, регулярными либо нерегулярными.

Характерная особенность волнового процесса в волноводе – наличие спектра собственных значений для постоянной распространения и соответствующих функций поперечного сечения, которые в совокупности характеризуют нормальную волну как элементарную форму волнового процесса в волноводе.

Изучение взаимодействия звуковых волн со средой восходит к классическим работам Стокса и Киргоффа, которые дали оценку поглощения звука в среде при учёте вязкости и теплопроводности. Эти механизмы поглощения имеют место на любых частотах. Однако, наибольший интерес представляют механизмы аномального поглощения звука с частотной зависимостью резонансного либо релаксационного типа. Наиболее интересны механизмы, происходящие на молекулярном либо квантовом уровне, а также механизмы, приводящие к усилению звука, например, в пьезополупроводниках.

Нелинейные эффекты в акустике обычно малы, но их влияние приводит к качественно новым эффектам, которые и представляют обычно наибольший интерес. Так, например, коэффициент нелинейного преобразования по мощности в параметрических излучателях составляет , но этого достаточно для практического их использования в прикладной гидроакустике. Нелинейные эффекты в колебательных системах могут приводить к потере устойчивости самой колебательной системы и разрушению. В основе кавитации также лежат нелинейные процессы, приводящие к схлопыванию воздушных пузырьков, растворённых в воде, при прохождении звуковой волны, а сам процесс схлопывания сопровождается образованием мощных ударных волн, разрушающих металл.

Нелинейная акустика – наименее изученный раздел акустики, но и самый перспективный, т.к. реальные процессы всегда являются скорее нелинейными, чем линейными.