1.3.5. Обобщёные волны Релея-Стонели-Шолте

на границе раздела жидкость-твёрдое тело.

Волна Стонели-Шолте является единственной волной поверхностного типа, локализованной вблизи границы раздела по всем своим составляющим.

В отличие от неё волна Релея, существующая на свободной границе твёрдого тела как незатухающая волна, при наличии жидкости становится волной вытекающей, амплитуда которой экспоненциально убывает при удалении от границы раздела в твёрдом полупространстве, экспоненциально растёт в жидком полупространстве и экспоненциально затухает в направлении распространении в обоих полупространствах.

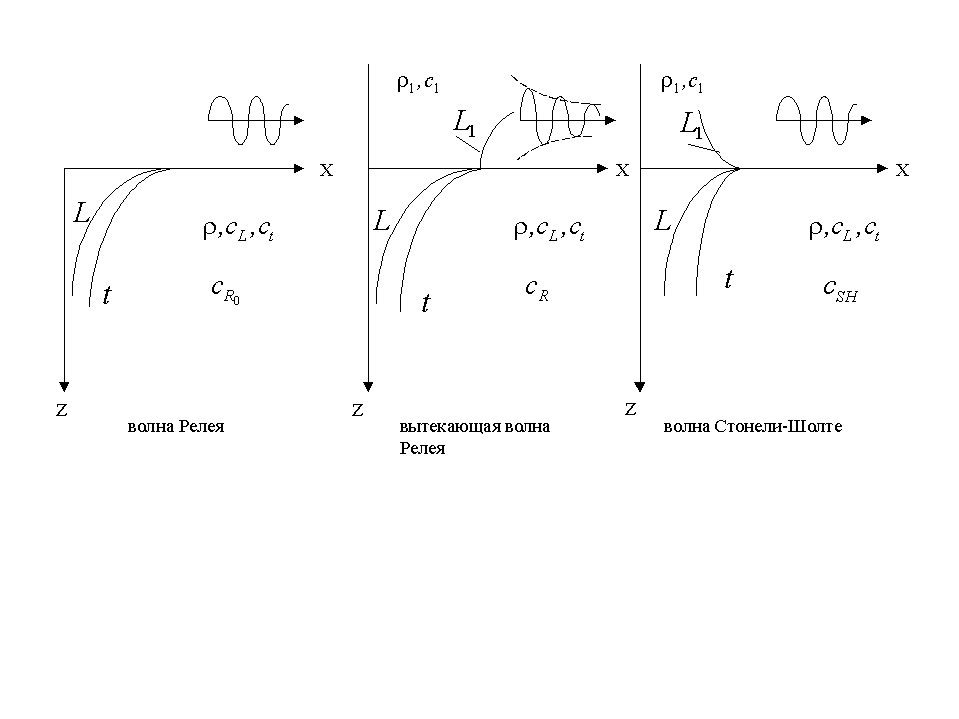
1.2.13. Поверхностные гравитационные волны.

Так, например, для границы раздела вода-сталь постоянная распространения становится комплексной , , а изменение скорости волны Релея составляет при изменении .

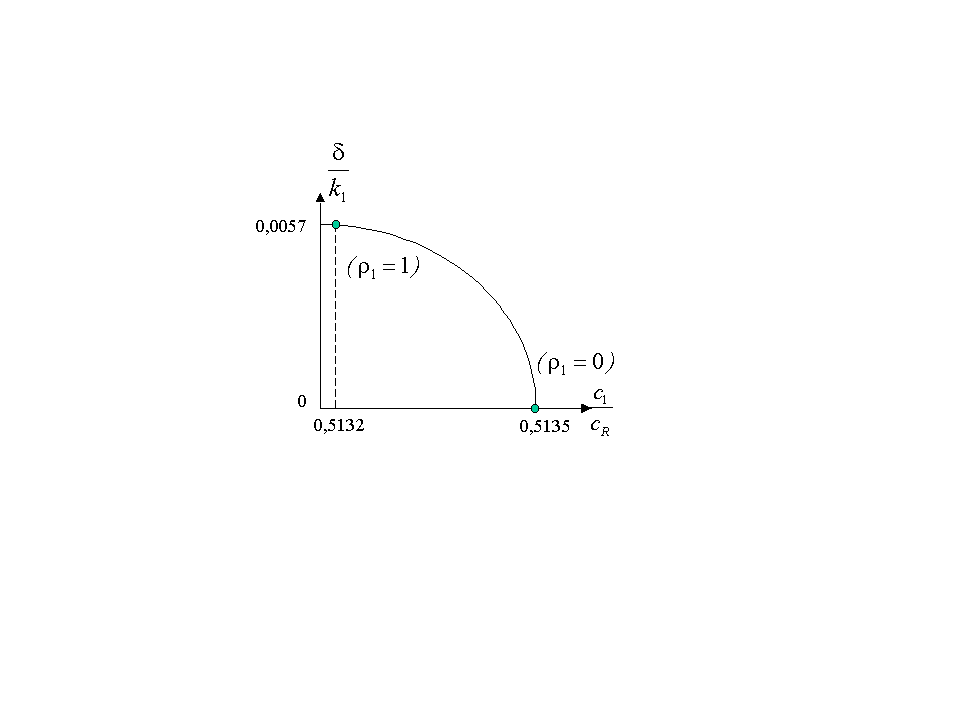
В случае , который имеет место для материалов типа пластика, плексигласа, на границе раздела жидкость-твёрдое тело возможно существование незатухающих (невытекающих) обобщённых поверхностных волн двух типов, которые называют обобщёнными волнами Релея-Стонели-Шолте.

а) Поливинилхлорид-вода. б) Плексиглас-вода.

, .

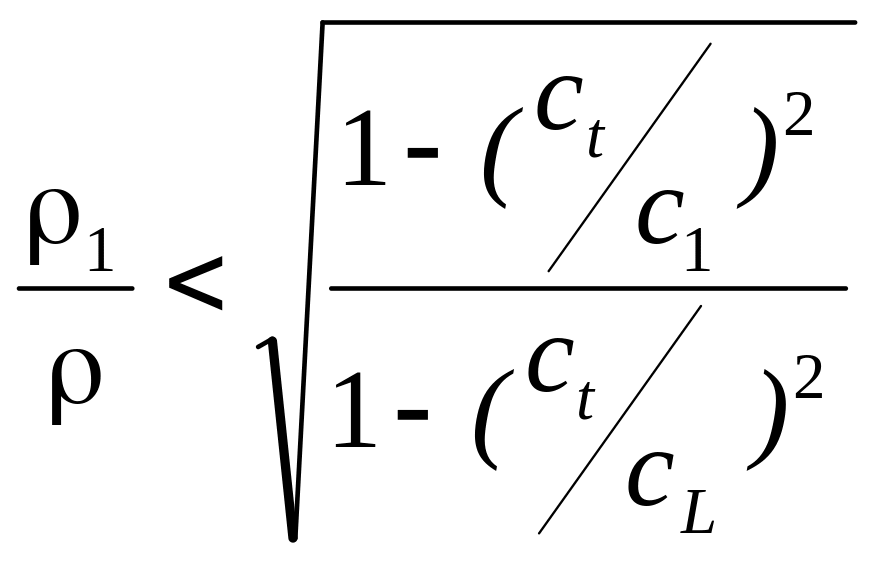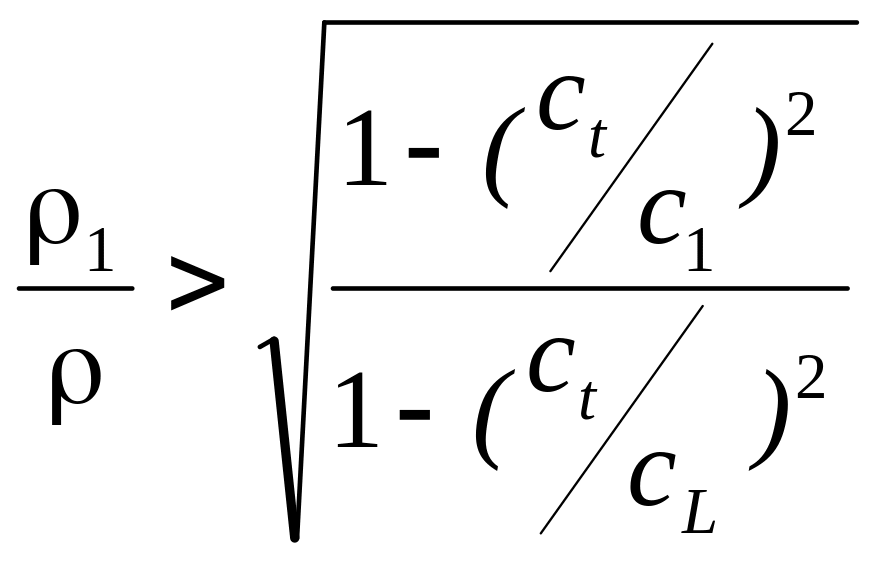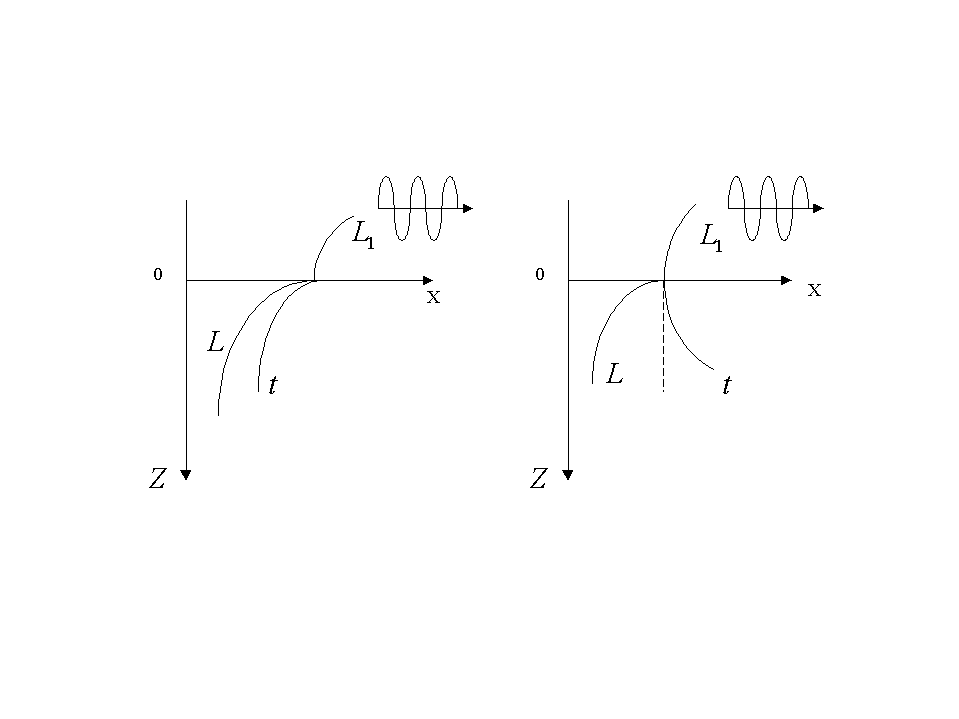
Для волны первого типа (случай а)) поле в твёрдом теле экспоненциально убывает при удалении от границы раздела по продольной и поперечной составляющим, но поле в жидкости экспоненциально растёт.

Для волн второго типа (случай б)) поле в твёрдом теле экспоненциально убывает по продольной составляющей, экспоненциально растёт по поперечной составляющей и экспоненциально растёт в жидкости.

В обоих случаях скорость обобщённой волны Релея-Стонели-Шолте больше скорости регулярной волны Стонели-Шолте, но меньше скорости .

Все составляющие, амплитуда которых экспоненциально растёт, должны описываться обобщёнными функциями, ограниченными на бесконечности и разрывными на границе раздела.

1.3.6. Поверхностные гравитационные волны.

Поверхностные волновые процессы играют важную роль в физике океана и атмосферы, а ветровое волнение на поверхности моря является источником шумовых процессов, распространяющихся вглубь моря. В формировании поверхностного волнения существенную роль играют силы гравитации на низких частотах и силы поверхностного натяжения на высоких частотах.

При рассмотрении гравитационных волн уравнение движения в потенциальном поле силы тяжести нужно записать следующим образом:

. (1.40.)

- потенциал силы притяжения ( ), - давление (полное) в жидкости, - ускорение силы тяжести.

.

Рассматривают или стационарное потенциальное движение жидкости , или нестационарное в приближении .

В первом случае уравнение (1.40.) переходит в уравнение Бернулли:

, которое выражает закон сохранения энергии, отнесённой к единице объёма, кинетической, внутренней и потенциальной.

Во втором случае (1.40.) переходит в уравнение:

.

Пусть поверхность воды описывается функцией отклонения уровня от стационарного:

При отклонении уровня воды от стационарного силы гравитации будут играть роль восстанавливающей силы, причём сжимаемостью воды можно пренебречь. В этом приближении потенциал скорости удовлетворяет уравнению Лапласа:

, а решение волнового типа имеет вид:

. (1.41.)

Решение для функции отклонения уровня запишем в виде поверхностной волны:

. (1.42.)

Система уравнений (1.41.), (1.42.) решается при граничных условиях на поверхности :

(кинематическое условие),

(условие на свободной поверхности).

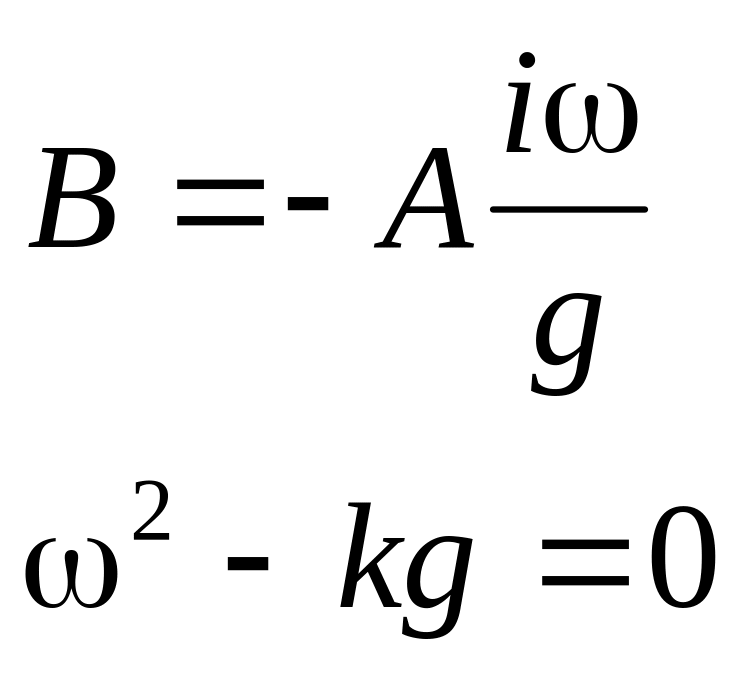. (1.43.)

Уравнение (1.43.) есть дисперсионное уравнение гравитационных волн на поверхности воды:

,

закон дисперсии был предсказан ещё Ньютоном.

Основные величины, описывающие движение в поверхностной волне:

,

.

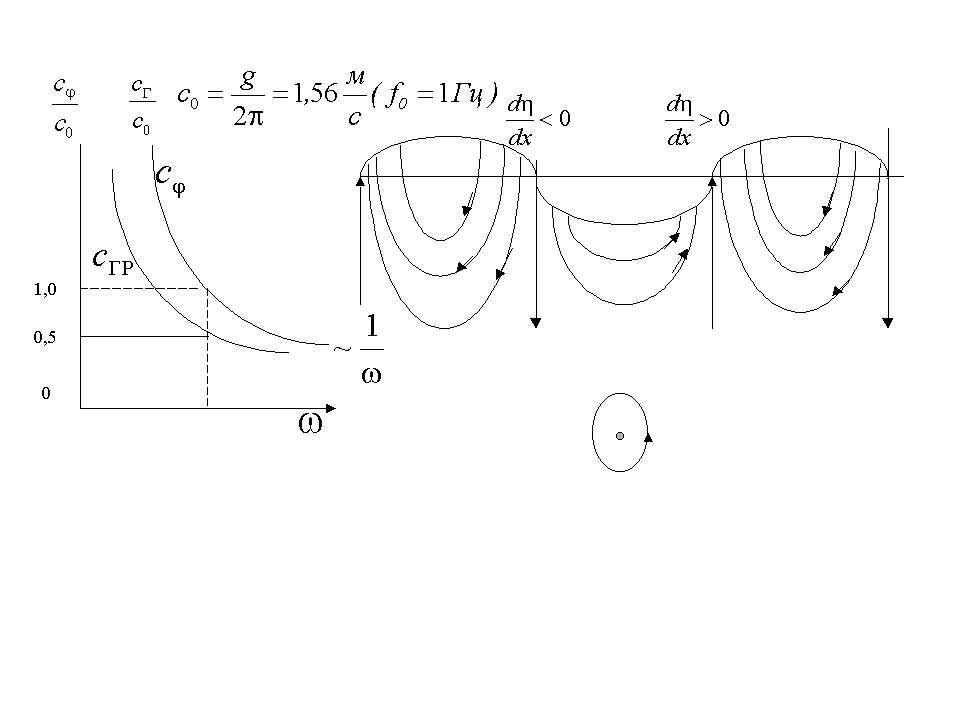
Сдвиг компонент колебательной скорости по фазе на свидетельствует о том, что частицы среды в такой волне движутся по круговым траекториям, а векторные линии тока замкнуты: вода перетекает со спадающего участка волны на поднимающийся.