
Расчетно-графическая работа №120
.docМинистерство образования и науки РФ
Уфимский Государственный Авиационный Технический Университет
Кафедра теоретических основ электротехники
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 1
«РАСЧЕТ ЛИНЕЙНОЙ ЦЕПИ ПОСТОЯННОГО ТОКА»
Выполнил:
Студент группы
Принял:
Заико А. И.
Уфа - 2007
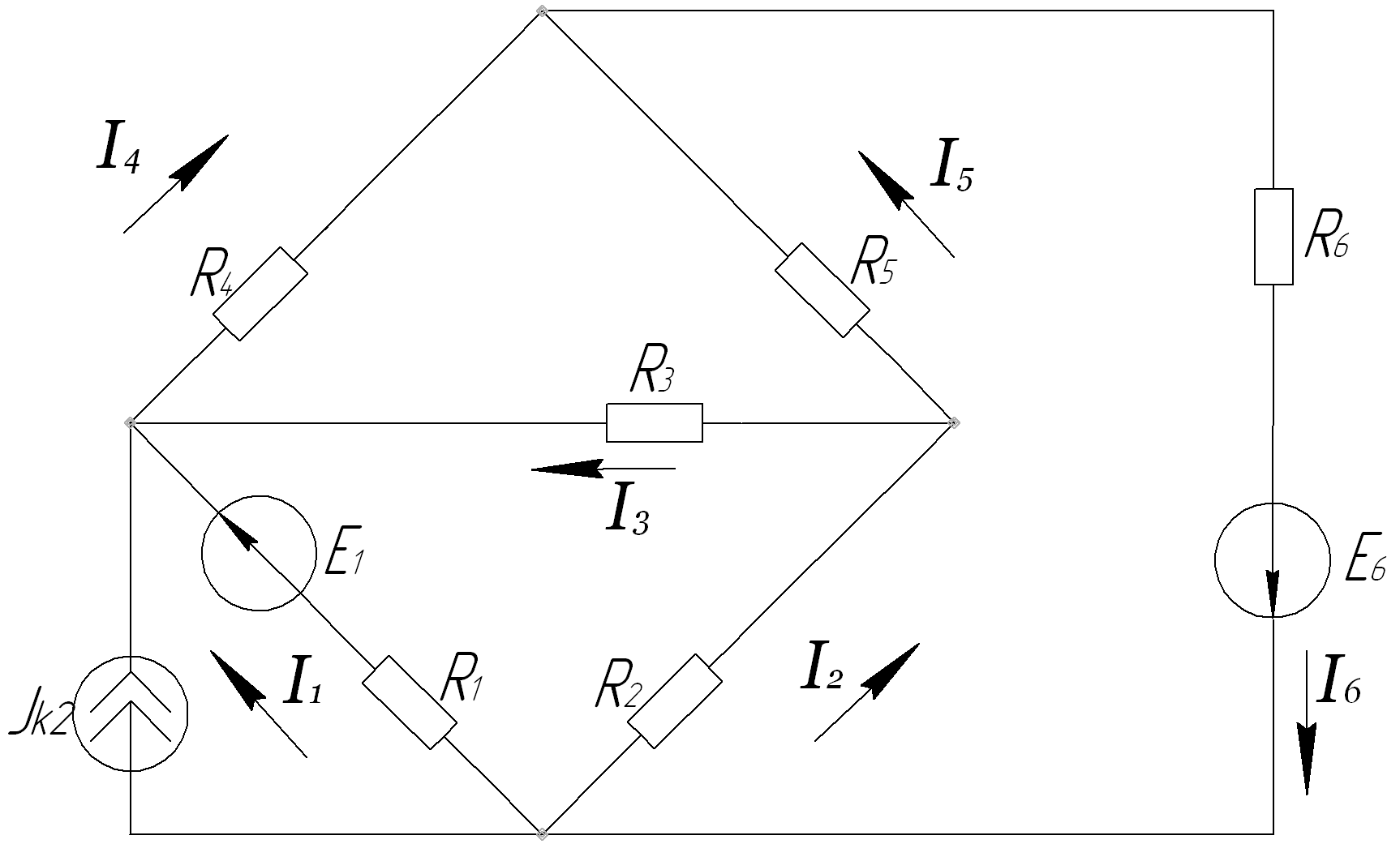
В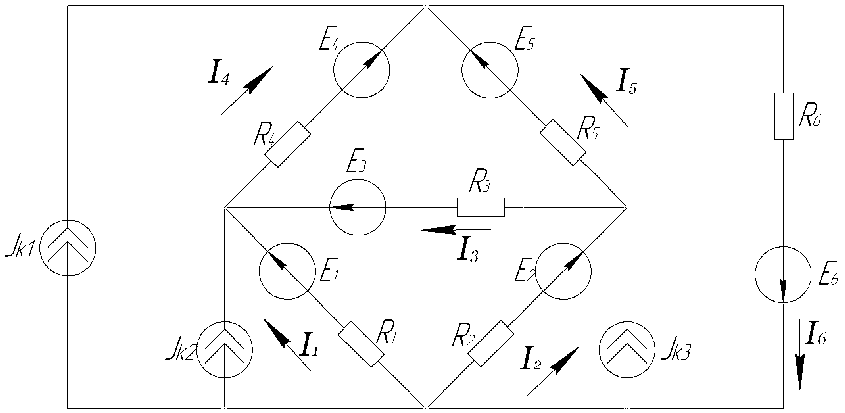 ариант
223999 - 2
ариант
223999 - 2
|
|
|
|
|
R1=10 |
R2=90 |
R3=10 |
|
R4=80 |
R5=10 |
R6=80 |
|
Е1=-450 |
Е2=0 |
|
|
Е3=0 |
Е4=0 |
|
|
Е5=0 |
Е6=200 |
|
|
IК1=0 |
IК2= - 3 |
|
|
IК3= 0 |
|
|
Расчёт цепи методом контурных токов
Введём контурные токи I11,I22,I33, I44, причём контурный ток I11 является известным и равным току источника тока IК2:
 I1=
I22
– I11
I1=
I22
– I11
I2= I44 – I22
I3= I33 – I22
I4= I33
I5= I44 – I33
I6= I44
Запишем уравнения по методу контурных токов:
 I11
= IК2
I11
= IК2
R21 I11 + R22 I22 + R23 I33 + R24 I44 = E22
R31 I11 + R32 I22 + R33 I33 + R34 I44 = E33
R41 I11 + R42 I22 + R43 I33 + R44 I44 = E44
 I11
= IК2
I11
= IК2
–R1 I11 + (R2+R3+R1)I22 – R3 I33 – R2I44 = E1
0 I11 – R3 I22 + (R4+R5+R3)I33 – R5I44 = 0
0 I11 – R2 I22 – R5 I33 + (R2+R5+R6)I44= E6
( R2+R3+R1)I22
– R3
I33
– R2I44
= E1
+
R1IК2
R2+R3+R1)I22
– R3
I33
– R2I44
= E1
+
R1IК2
R3I22 + (R4+R5+R3)I33 – R5I44 = 0
R2I22 – R5 I33 + (R2+R5+R6)I44= E6
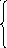
110I22 – 10 I33 – 90 I44 = –450 + 10(–3)
-10I22 + 100I33 – 10 I44 = 0
-90I22 – 10 I33 + 180I44 = 200
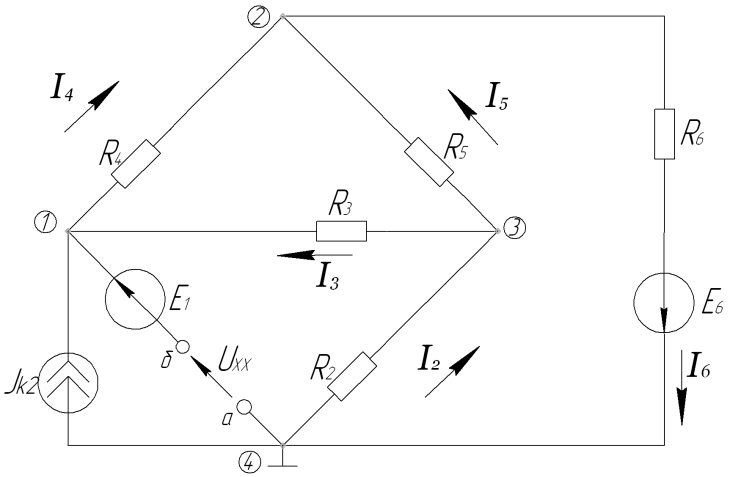
Составим матрицу и найдём контурные токи:
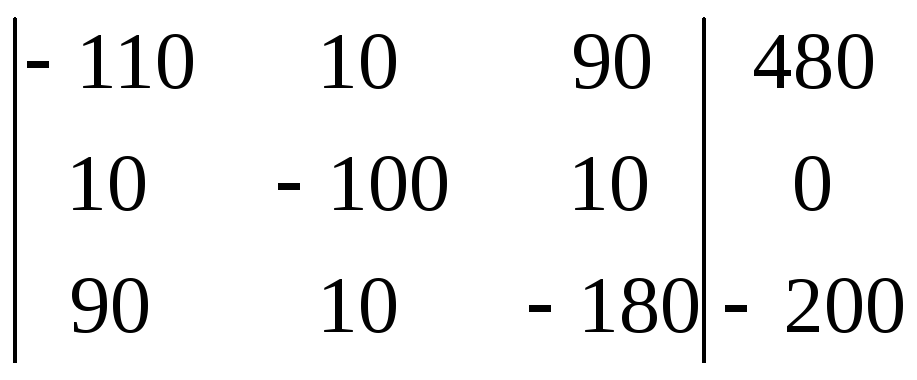
![]()
I11 = –3А, I22 = -6,030A, I33 = -0,7978A, I44 = -1,948A
Находим реальные токи

Расчёт цепи методом узловых потенциалов
Определяем количество необходимых уравнений n = У – 1 = 4 – 1 = 3.
Приняв потенциал точки 4 равным нулю, запишем систему уравнений
 φ1
G11
+ φ2
G12
+ φ3
G13
= I11
φ1
G11
+ φ2
G12
+ φ3
G13
= I11
φ1 G21 + φ2 G22 + φ3 G23 = I22
φ1 G31 + φ2 G32 + φ3 G33 = I33
Определяем взаимную и собственную проводимости
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
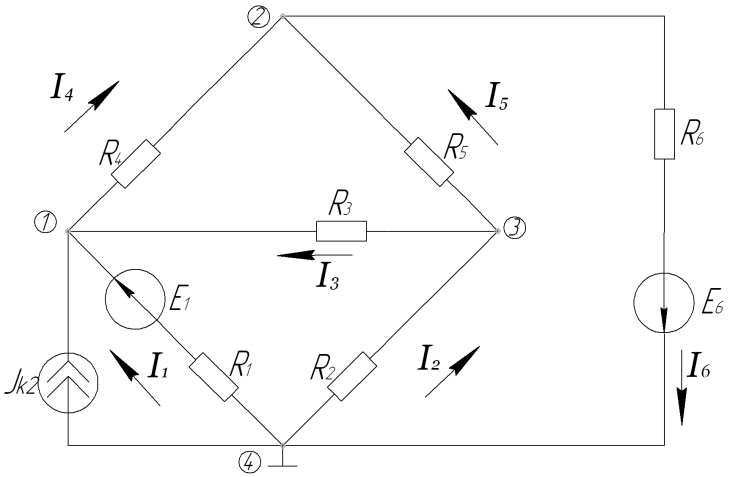
Составим матрицу и найдём потенциалы точек
φ1 = -419,70В φ2 = -355,873 В φ3 = -367,378 В φ4 = 0 В
Пользуясь законом Ома, определяем токи во всех ветвях
![]()
![]()
![]()
![]()
![]()
![]()
Таблица токов
|
Токи |
I1,А |
I2,А |
I3,А |
I4,А |
I5,А |
I6,А |
|
МКТ |
-3,030 |
4,082 |
5,232 |
-0,7978 |
-1,15 |
-1,948 |
|
МУП |
-3,03 |
4,0819 |
5,232 |
-07978 |
-1,1505 |
-1,9484 |
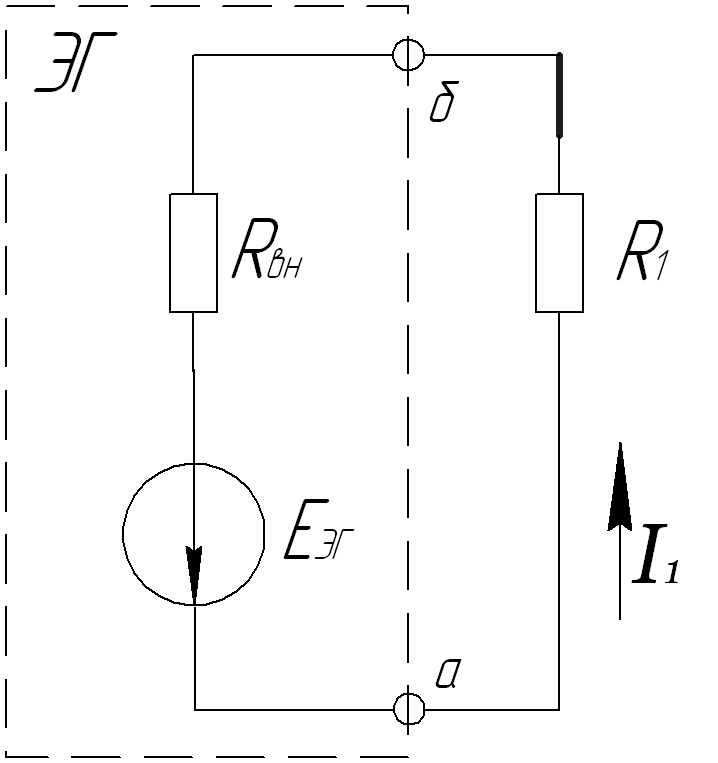
Определение тока I1 методом эквивалентного генератора
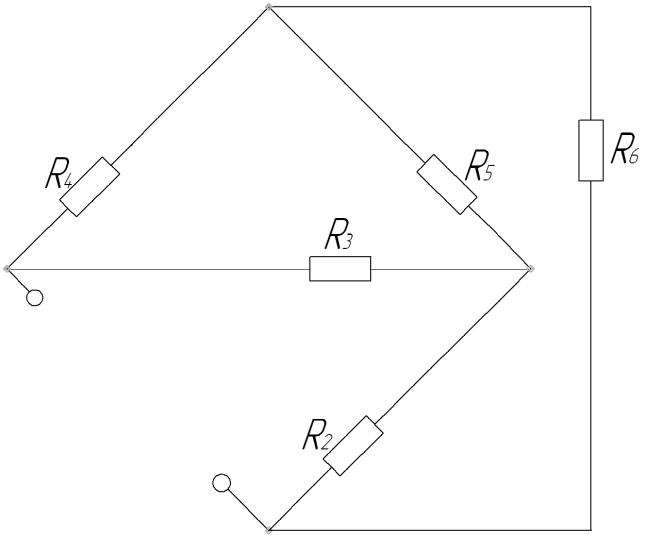
Сначала определим потенциалы 1-го узла в отсутствии сопротивлением R1, приняв потенциал 4-го узла за ноль.
φ1 G11 + φ2 G12 + φ3 G13 = I11
φ1 G21 + φ2 G22 + φ3 G23 = I22
φ1 G31 + φ2 G32 + φ3 G33 = I33

![]()

φ1 = – 597,11934 В; φ2 = –458,84774 В; φ3 = –531,27572В; φ4 = 0 В
U41 = φ4 – φ1
U41 = Uxx – UE1
Uxx = U41 + UE1= φ4 – φ1 + E1 = 0 – (–597,11934) + (-450) = 147,11934 В
Определим RВН эквивалентного генератора. Проведём преобразования схемы.
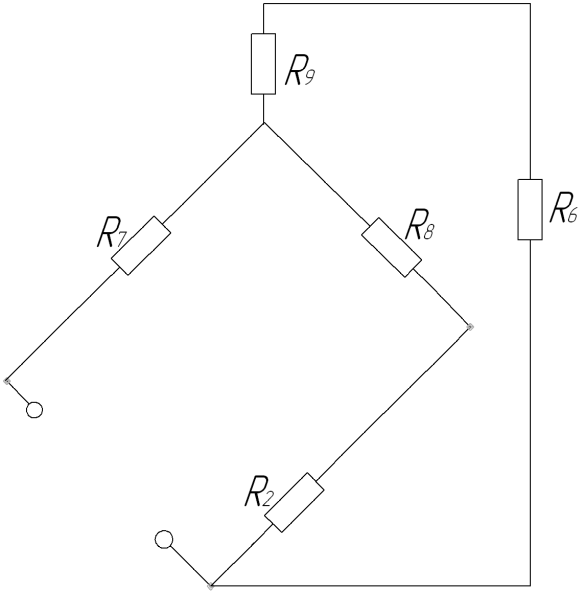



![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]()
![]()
![]()
4. Баланс мощностей
ΣPист = ΣPпр.
ΣPист = ΣPE + ΣPJ
ΣPE = E1 I1 + E6 I6 = –450∙(-3,03) + 200∙(–1,9484) = 973,82 Вт
ΣPJ = UJk2 Jk2
Из второго закона Кирхгофа найдём UJk2
UJk2 +I2R2 + I3R3 = 0
UJk2 = –(I2R2 + I3R3) = –419,691 В
ΣPJ = UJk2 Jk2 = –419,691 ∙(–3) = 1259,073 Вт
ΣPист = ΣPE + ΣPJ = 2232,893 Вт
ΣPпр = R1 I12 + R2 I22 + R3 I32 + R4 I42 + R5 I52 + R6 I62 = 91,809 + 1499,57168 + 273,73824 + 50,91878 + 13,2365 + 303,701 = 2232,9752 Вт
ΣPист = 2232,893 ≈ 2232,9752 = ΣPпр
ΣPист
![]() ΣPпр
ΣPпр
Баланс соблюдается.
